FIND STRONGLY CONNECTED COMPONENTS USING KOSARAJUS ALGORITHM AND

FIND STRONGLY CONNECTED COMPONENTS USING KOSARAJU’S ALGORITHM AND TARJAN’S ALGORITHM National Chiao Tung University Department of Electronics Engineering

OUTLINE What is strongly connected components (SCC) ? 2 properties of SCC. How Kosaraju’s Algorithm works. Complexity of Kosaraju’s Algorithm. How ’s Tarjan’s Algorithm works. Complexity of Tarjan’s Algorithm.

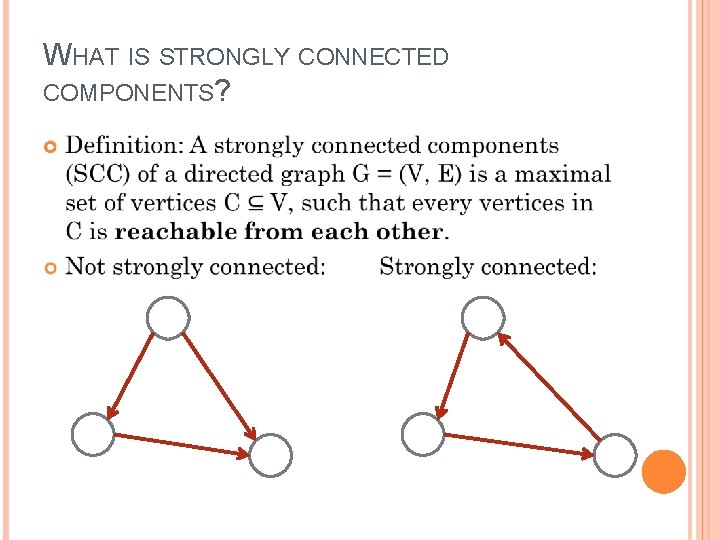
WHAT IS STRONGLY CONNECTED COMPONENTS?

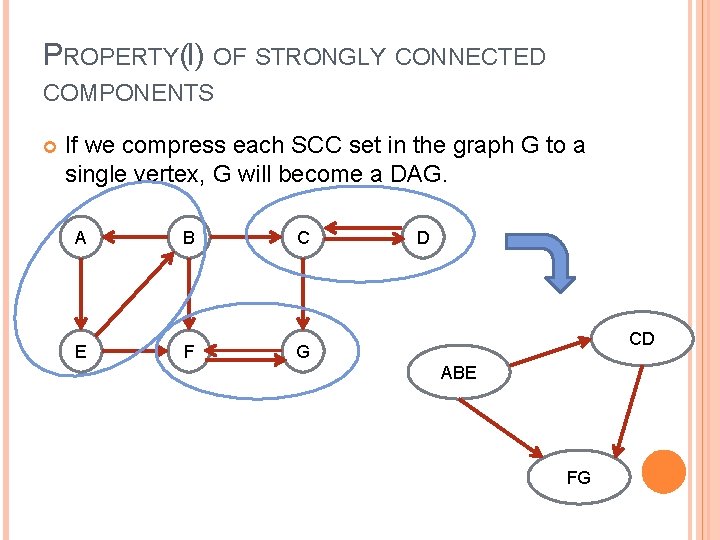
PROPERTY(I) OF STRONGLY CONNECTED COMPONENTS If we compress each SCC set in the graph G to a single vertex, G will become a DAG. A B C E F G D CD ABE FG

PROPERTY(I) OF STRONGLY CONNECTED COMPONENTS

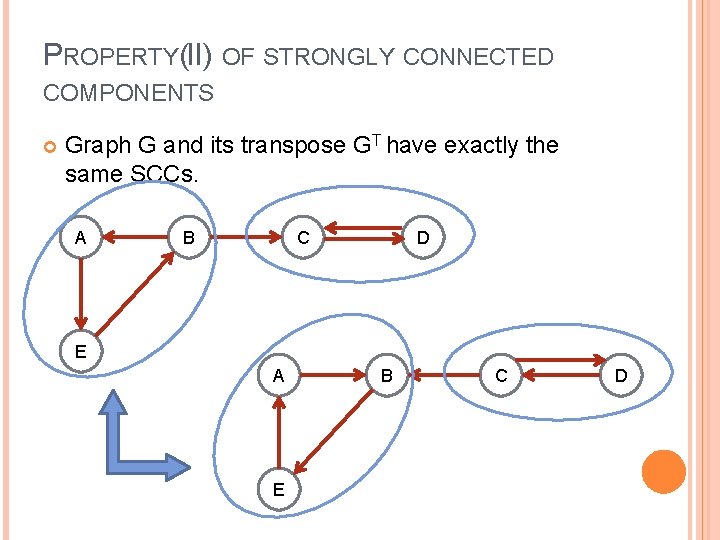
PROPERTY(II) OF STRONGLY CONNECTED COMPONENTS Graph G and its transpose GT have exactly the same SCCs. A B C D E A E B C D

PROPERTY(II) OF STRONGLY CONNECTED COMPONENTS Informal proof. A SCC set → vertices within it construct a cycle. Reverse the edges of a cycle → still a cycle. According to property I, we can transform graph G in to a DAG. Reverse the edges of a DAG → still a DAG. So the SCC sets of G is the same as GT ’s.

KOSARAJU’S ALGORITHM Make use of the second property of SCC. Kosaraju(G) 1. Run DFS(G) to compute finishing times u. f for each vertex u. 2. Compute GT. 3. Run DFS(GT), choose the vertices with the decreasing order of u. f calculated in step 1. 4. Put every vertex visited during each DFS iteration into current SCC set. 5. When current DFS iteration comes to an end, put current SCC set into SCC list, and start next DFS iteration from another unvisited vertex. 6. After all vertices are visited, we get a complete SCC list.

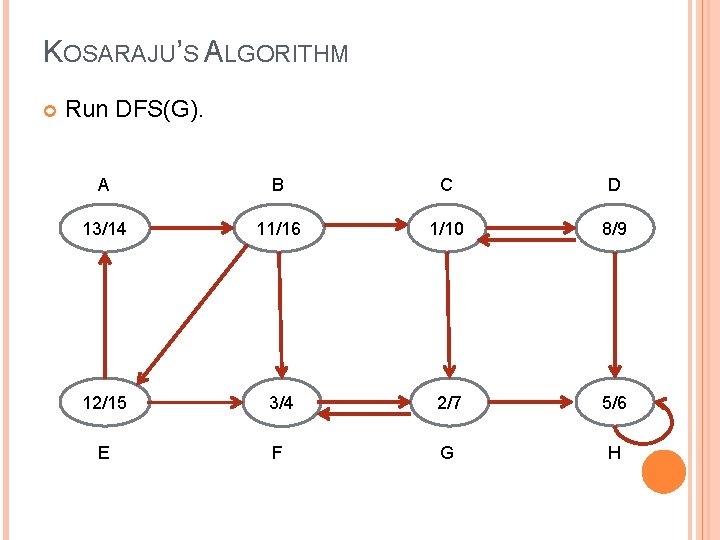
KOSARAJU’S ALGORITHM Run DFS(G). A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

KOSARAJU’S ALGORITHM Compute GT. A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

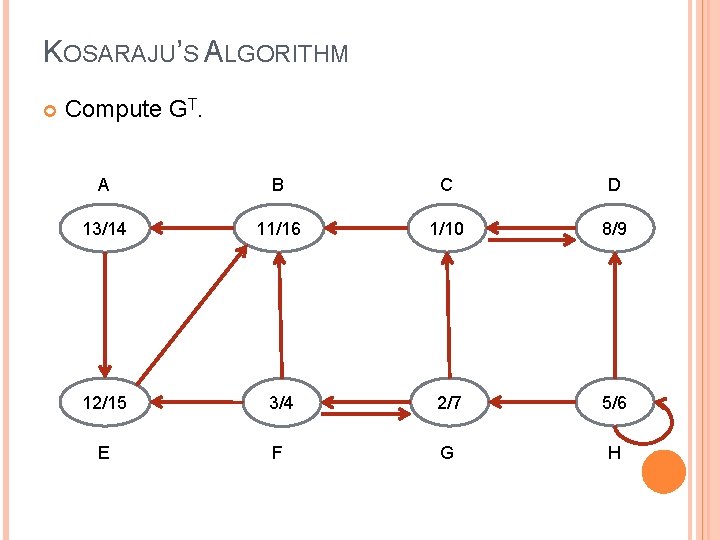
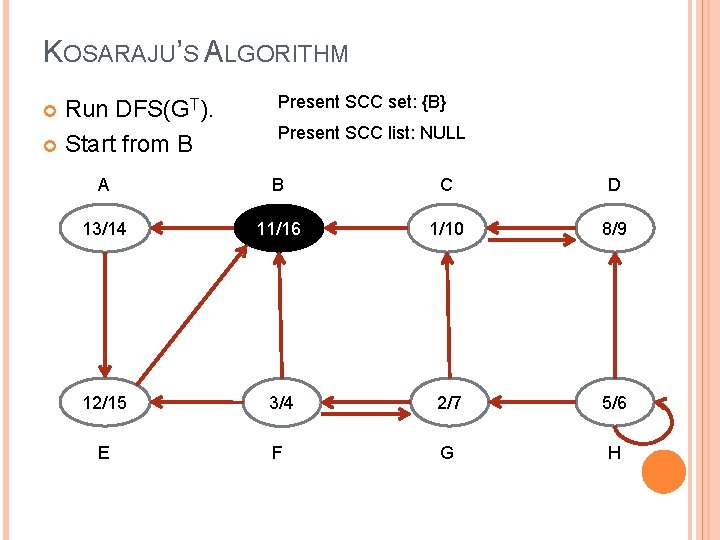
KOSARAJU’S ALGORITHM Run DFS(GT). Start from B Present SCC set: {B} Present SCC list: NULL A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

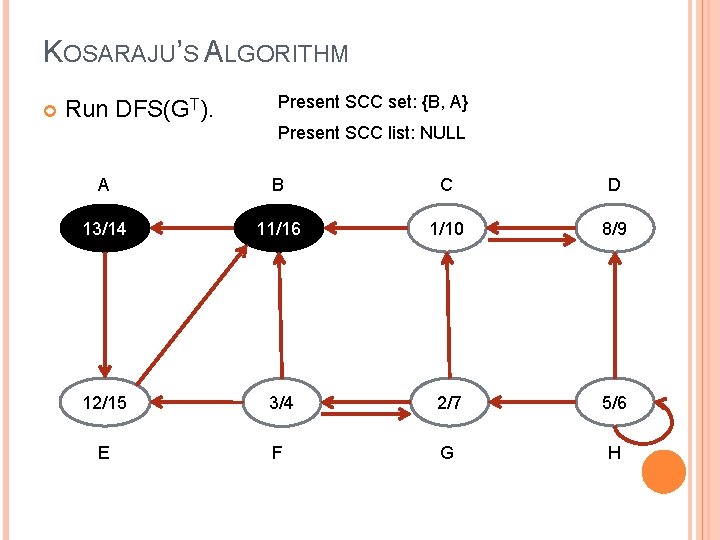
KOSARAJU’S ALGORITHM Run DFS(GT). Present SCC set: {B, A} Present SCC list: NULL A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

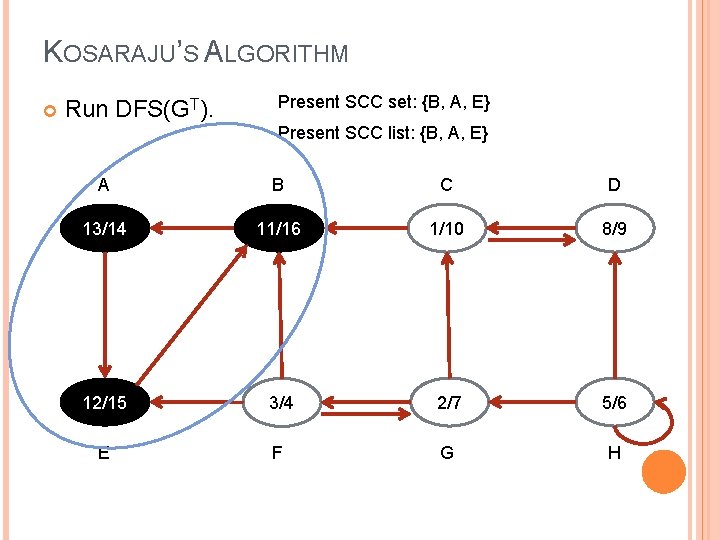
KOSARAJU’S ALGORITHM Run DFS(GT). Present SCC set: {B, A, E} Present SCC list: {B, A, E} A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

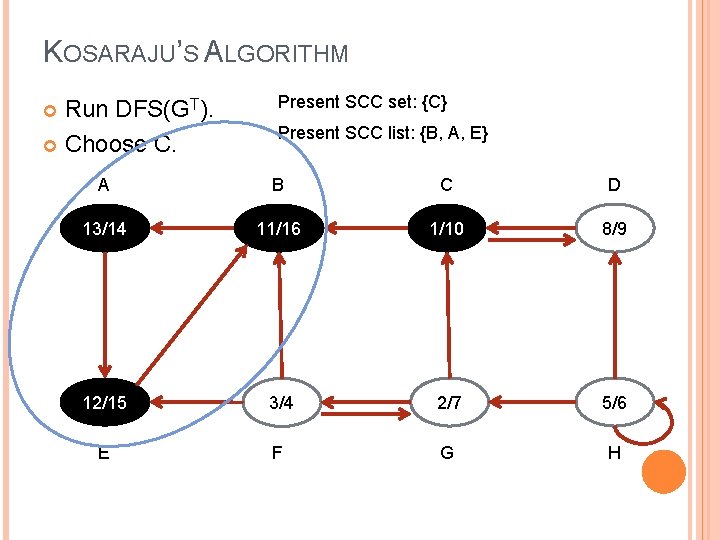
KOSARAJU’S ALGORITHM Run DFS(GT). Choose C. Present SCC set: {C} Present SCC list: {B, A, E} A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

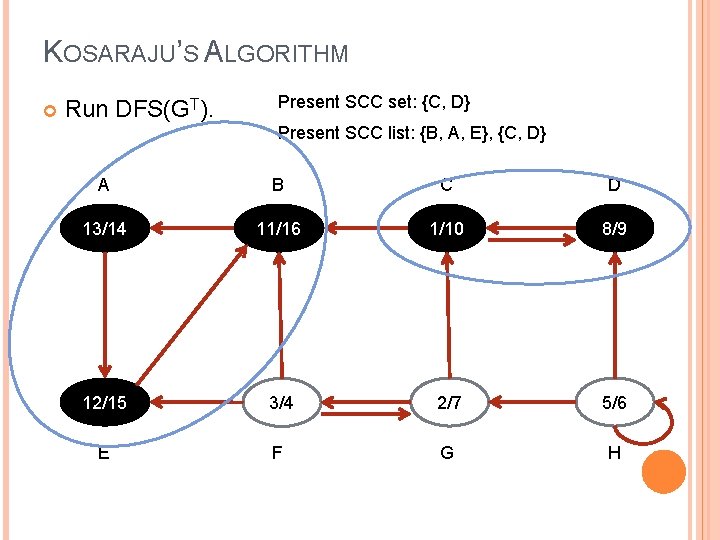
KOSARAJU’S ALGORITHM Run DFS(GT). Present SCC set: {C, D} Present SCC list: {B, A, E}, {C, D} A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

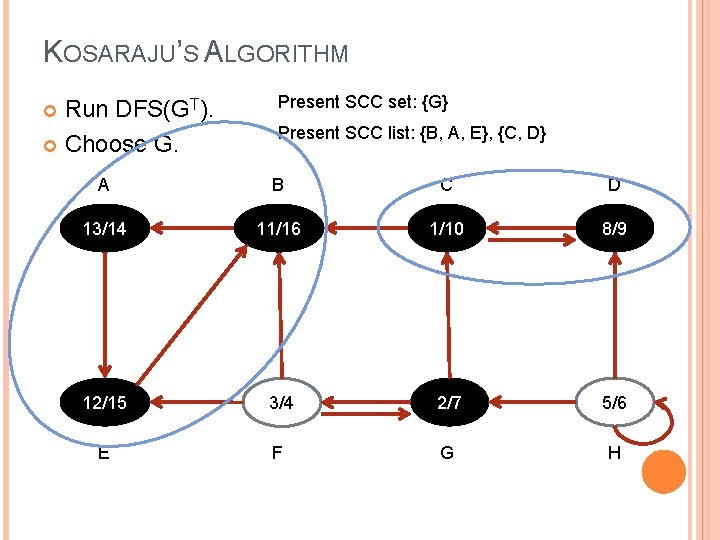
KOSARAJU’S ALGORITHM Run DFS(GT). Choose G. Present SCC set: {G} Present SCC list: {B, A, E}, {C, D} A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

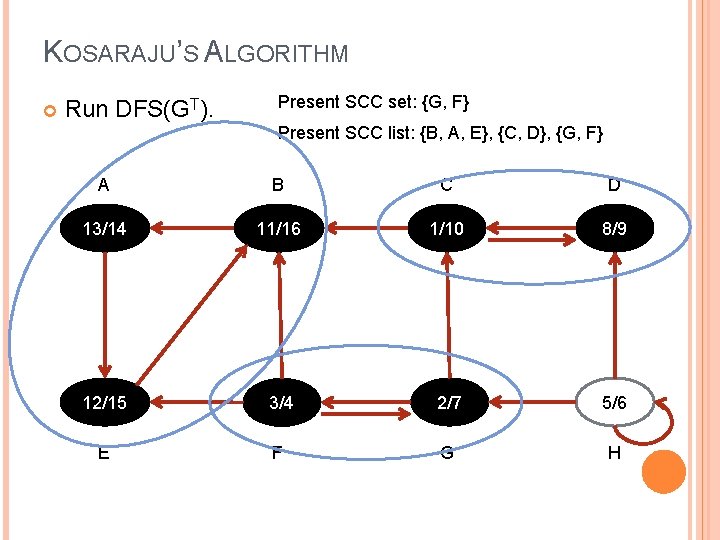
KOSARAJU’S ALGORITHM Run DFS(GT). Present SCC set: {G, F} Present SCC list: {B, A, E}, {C, D}, {G, F} A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

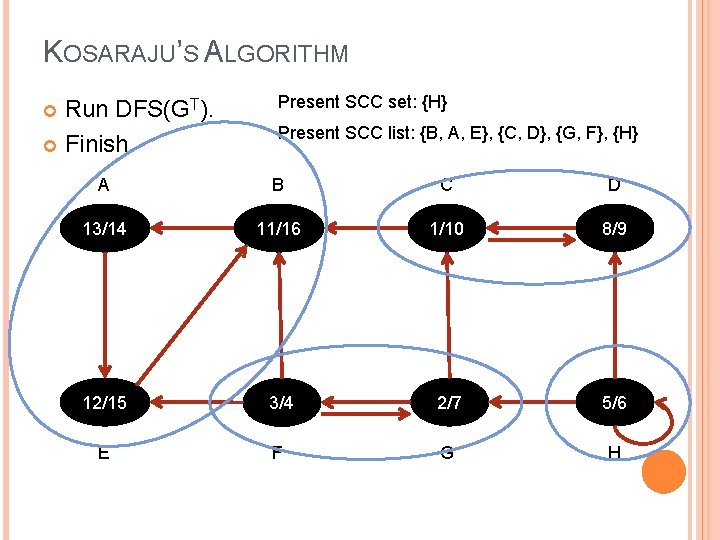
KOSARAJU’S ALGORITHM Run DFS(GT). Finish. Present SCC set: {H} Present SCC list: {B, A, E}, {C, D}, {G, F}, {H} A B C D 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 E F G H

WHY KOSARAJU’S ALGORITHM WORKS? According to Corollary 22. 15: Each edge in the transpose of G that goes between different SCC goes from a vertex with an earlier finishing time to one with a later finishing time. According to property I, we can compress the graph into a DAG. So, if we choose the vertex in the transpose of G to start DFS in the order of decreasing finishing time, we are actually visiting the DAG of SCC in the reverse topological order.

WHY KOSARAJU’S ALGORITHM WORKS? Because there is a two-way path between any pair of vertices in a SCC. We can traverse all the vertices in a SCC by DFS in any order. Because we visit the DAG of SCC in the reverse topological order. No matter how we traverse all vertices within a SCC by DFS, we won’t accidentally go into other SCC. The vertices we can visit by one time of DFS are constrained to the same SCC set. Remember to delete the whole SCC set from the graph once it is visited.

COMPLEXITY OF KOSARAJU’S ALGORITHM DFS x 2, G transpose x 1 Analysis: 1. Do DFS(G) first time. => Θ(V+E) / Θ(V^2) 2. Transpose G. => Θ(E) / 0 3. Do DFS(GT) and produce SCC sets. => Θ(V+E) / Θ(V^2) Using adjacency list: Θ(V+E) Using adjacency matrix: Θ(V^2)

TARJAN’S ALGORITHM Modified DFS. Every vertex in the SCC can be the root. Traverse every vertex, if a vertex v is unvisited, then it is the root of a new SCC. We call the funciton Tarjan(v). One time of DFS may produce multiple SCC sets. Some parameters: 1. v. index is the time stamp we discover vertex v; v. low is the index of oldest ancestor v can reach. 1/1 2/2 3/2 4/2

TARJAN’S ALGORITHM Tarjan(v) 1. Set both v. index, v. low to a global variable “t”. 2. ++t 3. Push v into the stack S. 4. Traverse every vertex directly reachable from v. If vertex w is unvisited, run Tarjan(w). Then set v. low = min{v. low, w. low}. b. If vertex w is visited, v. low = min{v. low, w. low} a. 5. 6. 7. 8. After the loop above, we can get the index of the oldest ancestor reachable from v (a. k. a. v. low). If (v. low == v. index), v is the root of the SCC. Pop the items in stack out until v is popped out. Those vertices compose a SCC.

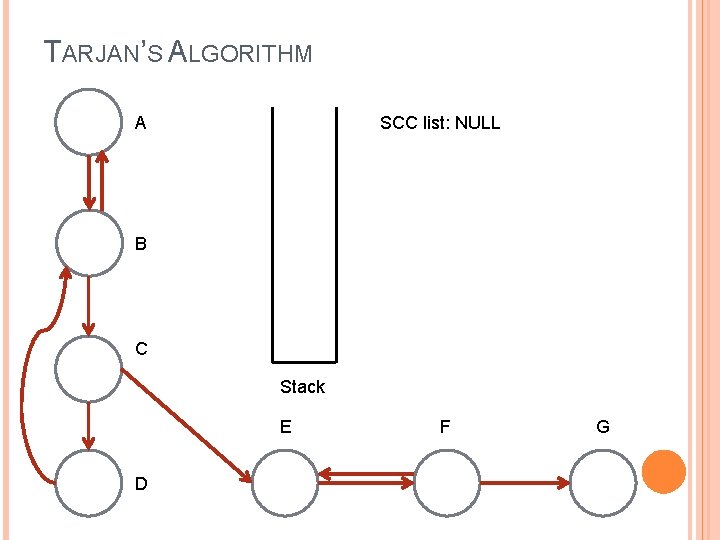
TARJAN’S ALGORITHM SCC list: NULL A B C Stack E D F G

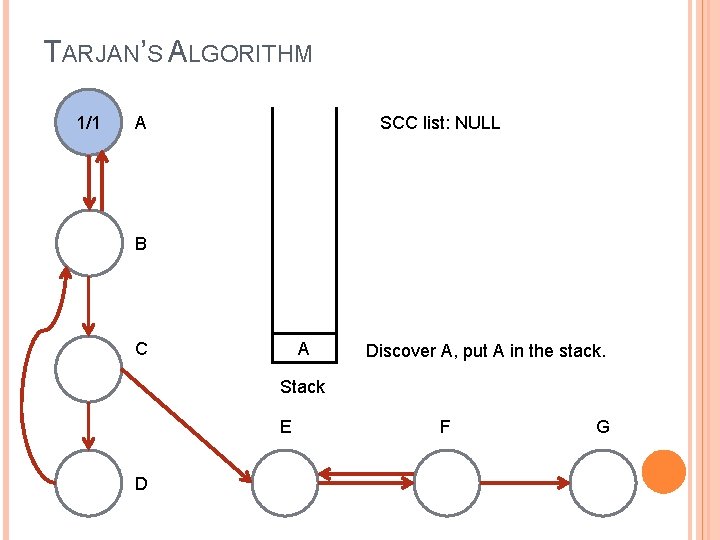
TARJAN’S ALGORITHM 1/1 SCC list: NULL A B C A Discover A, put A in the stack. Stack E D F G

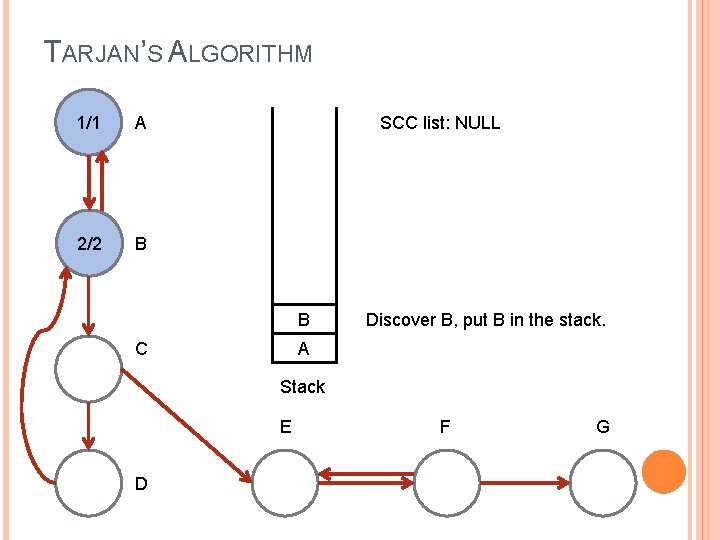
TARJAN’S ALGORITHM 1/1 A 2/2 B SCC list: NULL B C Discover B, put B in the stack. A Stack E D F G

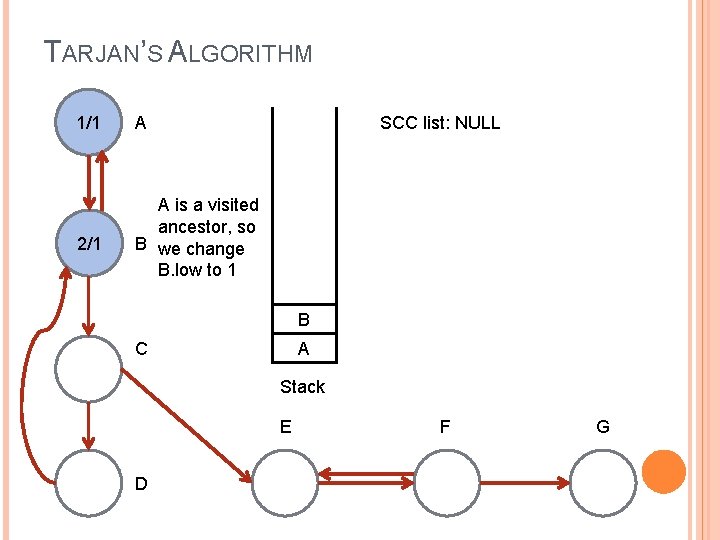
TARJAN’S ALGORITHM 1/1 A 2/1 A is a visited ancestor, so B we change B. low to 1 SCC list: NULL B C A Stack E D F G

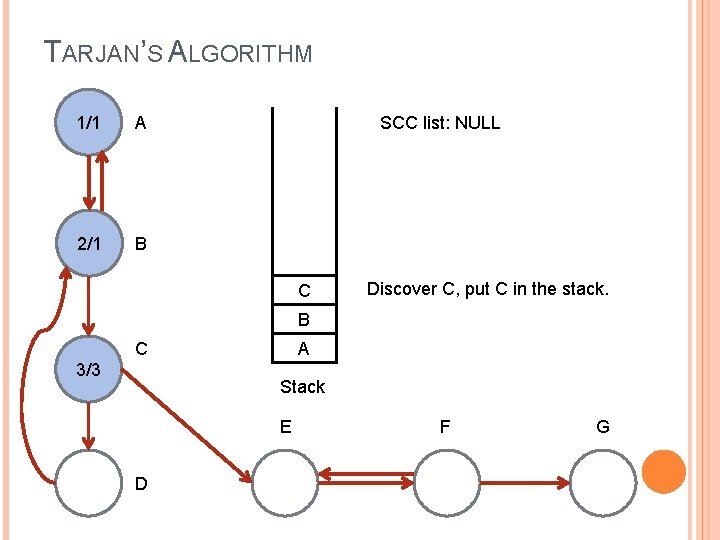
TARJAN’S ALGORITHM 1/1 A 2/1 B SCC list: NULL C Discover C, put C in the stack. B C 3/3 A Stack E D F G

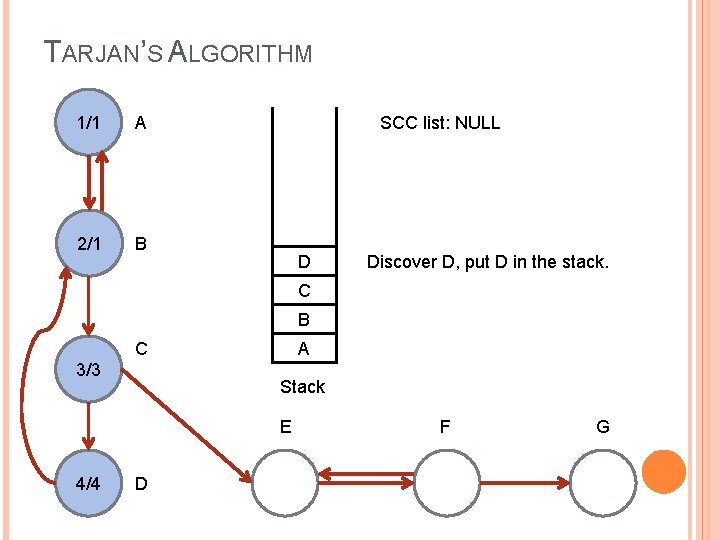
TARJAN’S ALGORITHM 1/1 A 2/1 B SCC list: NULL D Discover D, put D in the stack. C B C 3/3 A Stack E 4/4 D F G

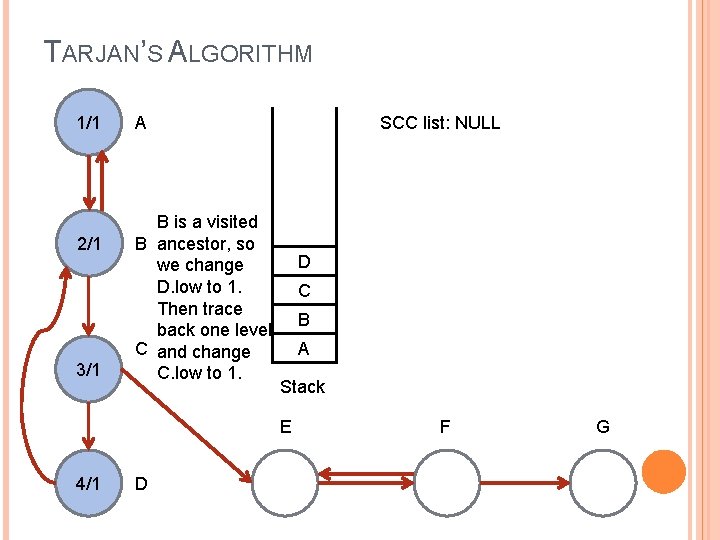
TARJAN’S ALGORITHM 1/1 2/1 3/1 SCC list: NULL A B is a visited B ancestor, so we change D. low to 1. Then trace back one level C and change C. low to 1. D C B A Stack E 4/1 D F G

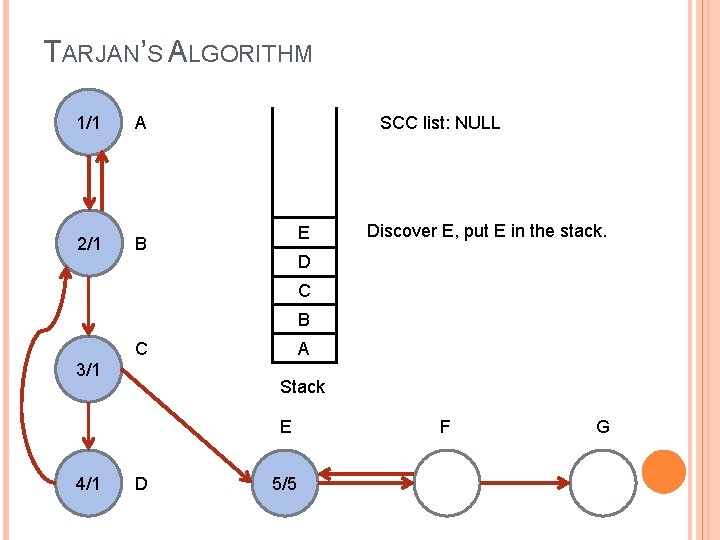
TARJAN’S ALGORITHM 1/1 A 2/1 B SCC list: NULL E Discover E, put E in the stack. D C B C 3/1 A Stack E 4/1 D 5/5 F G

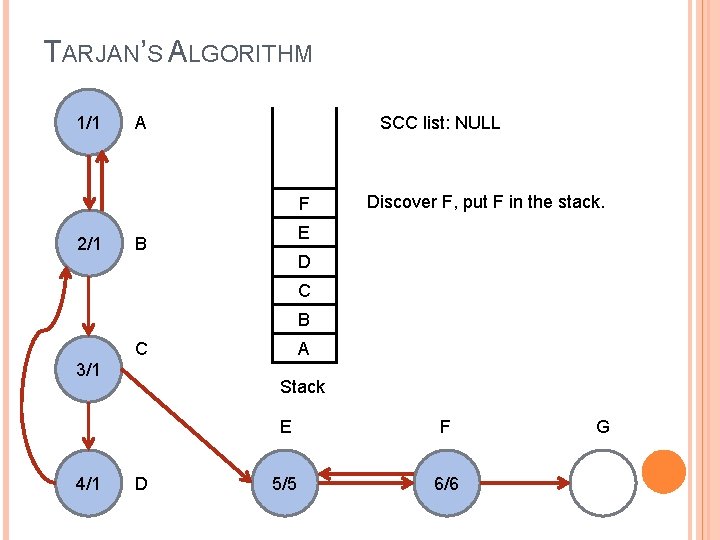
TARJAN’S ALGORITHM 1/1 SCC list: NULL A F 2/1 Discover F, put F in the stack. E B D C B C 3/1 4/1 A Stack D E F 5/5 6/6 G

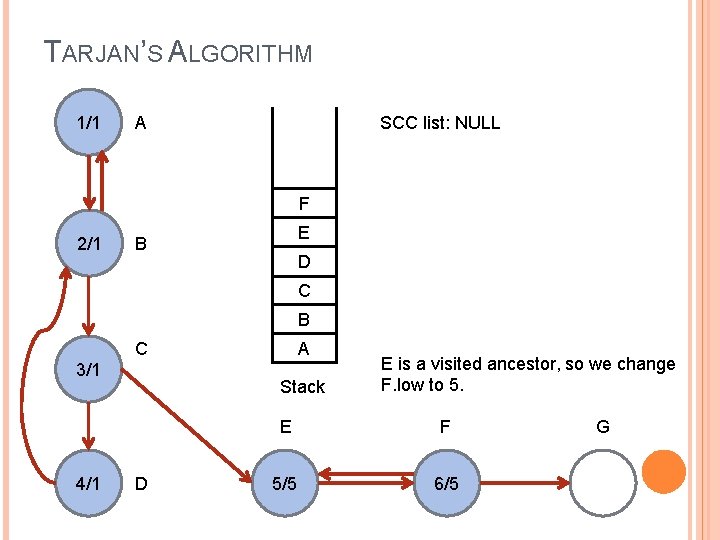
TARJAN’S ALGORITHM 1/1 SCC list: NULL A F 2/1 E B D C B C 3/1 4/1 A Stack D E is a visited ancestor, so we change F. low to 5. E F 5/5 6/5 G

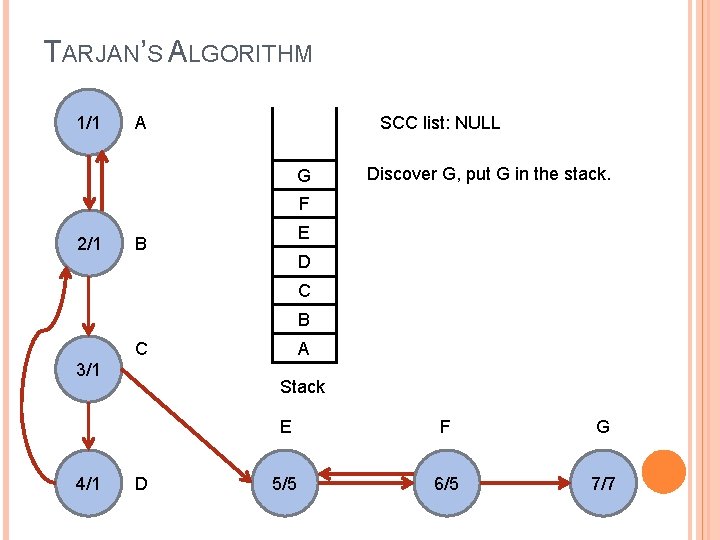
TARJAN’S ALGORITHM 1/1 SCC list: NULL A G Discover G, put G in the stack. F 2/1 E B D C B C 3/1 4/1 A Stack D E F G 5/5 6/5 7/7

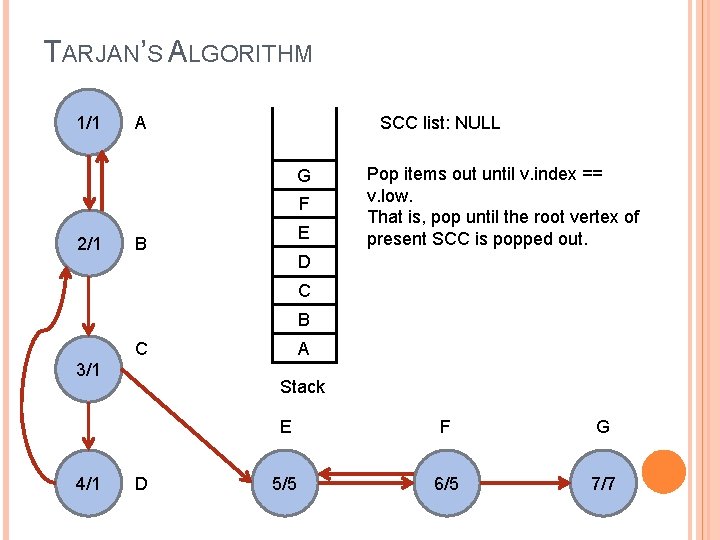
TARJAN’S ALGORITHM 1/1 SCC list: NULL A G F 2/1 E B Pop items out until v. index == v. low. That is, pop until the root vertex of present SCC is popped out. D C B C 3/1 4/1 A Stack D E F G 5/5 6/5 7/7

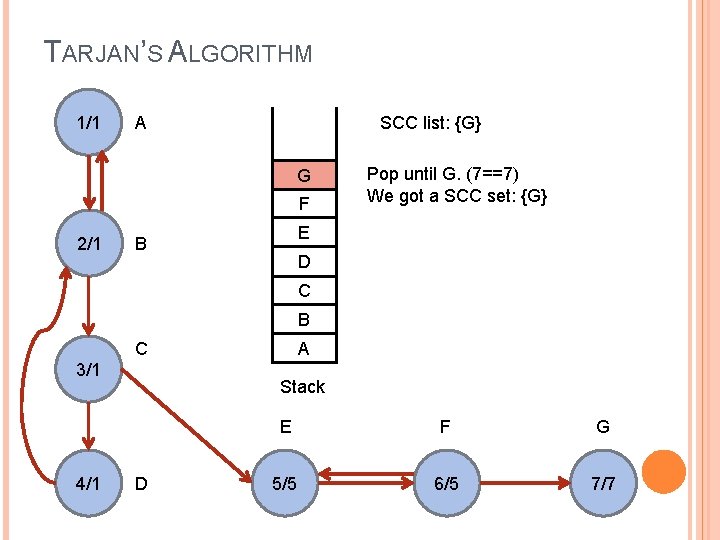
TARJAN’S ALGORITHM 1/1 SCC list: {G} A G F 2/1 Pop until G. (7==7) We got a SCC set: {G} E B D C B C 3/1 4/1 A Stack D E F G 5/5 6/5 7/7

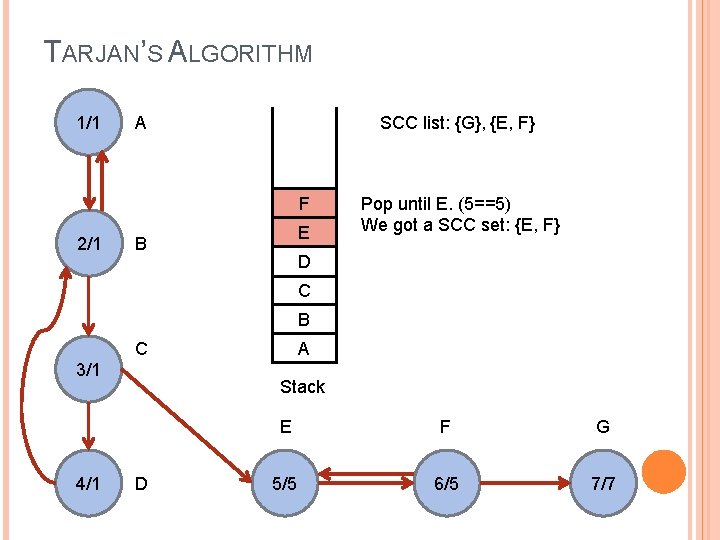
TARJAN’S ALGORITHM 1/1 SCC list: {G}, {E, F} A F 2/1 E B Pop until E. (5==5) We got a SCC set: {E, F} D C B C 3/1 4/1 A Stack D E F G 5/5 6/5 7/7

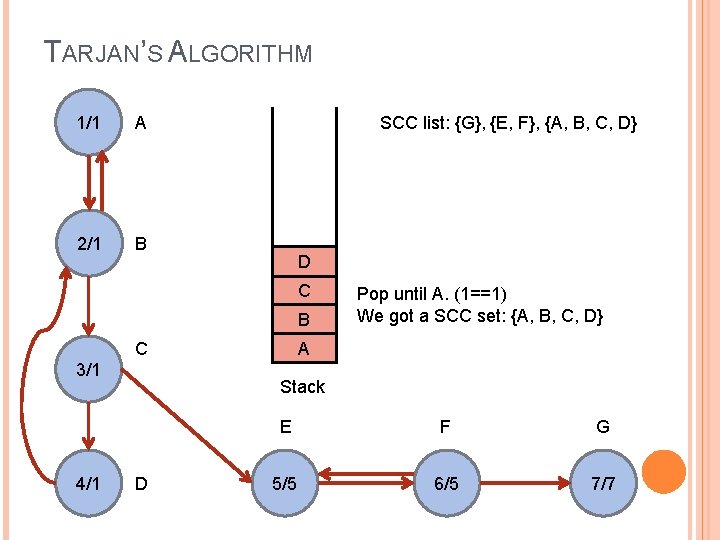
TARJAN’S ALGORITHM 1/1 A 2/1 B SCC list: {G}, {E, F}, {A, B, C, D} D C B C 3/1 4/1 Pop until A. (1==1) We got a SCC set: {A, B, C, D} A Stack D E F G 5/5 6/5 7/7

COMPLEXITY OF TARJAN’S ALGORITHM Total operation: DFS x 1 Analysis: 1. Discover every vertex and initialize v. index, v. low. => Θ(V) 2. Traverse every edge. => Θ(E) / Θ(V^2) 3. Pop items out and build SCC sets. => Θ(V) Using adjacency list: Θ(V+E) Using adjacency matrix: Θ(V^2)