FINANCIAL MATHS Grade 12 Paper I 1106 T






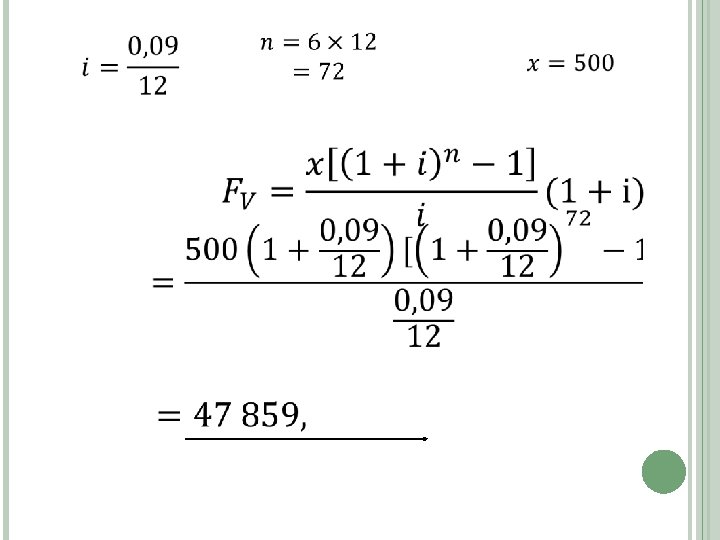












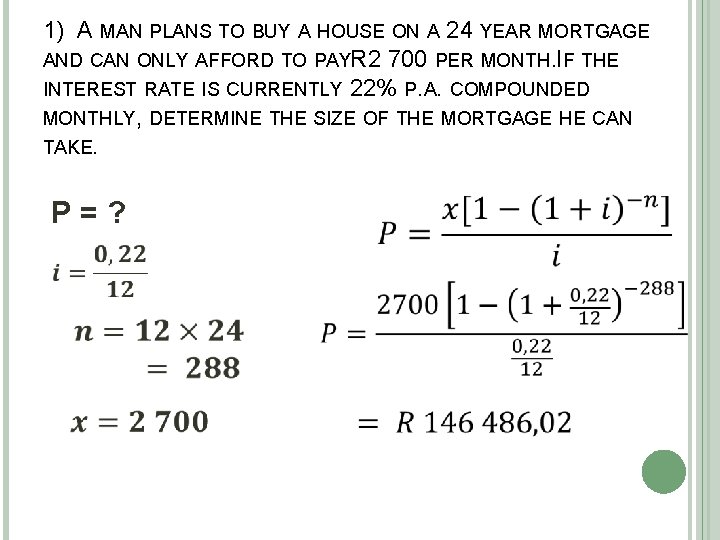

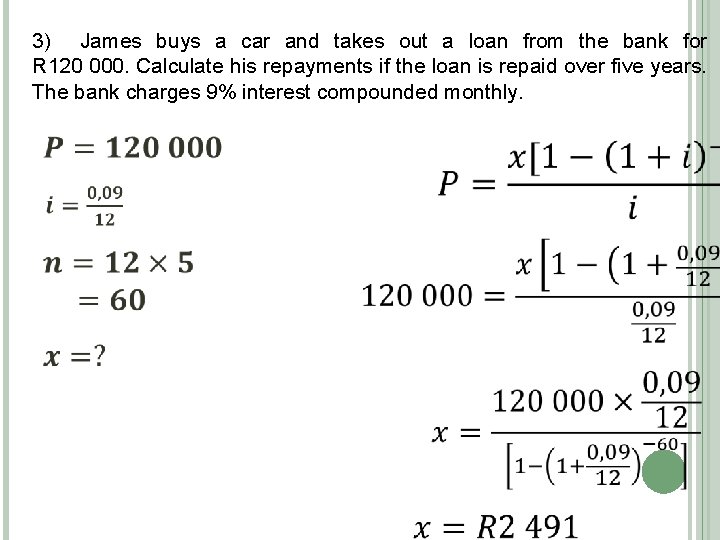













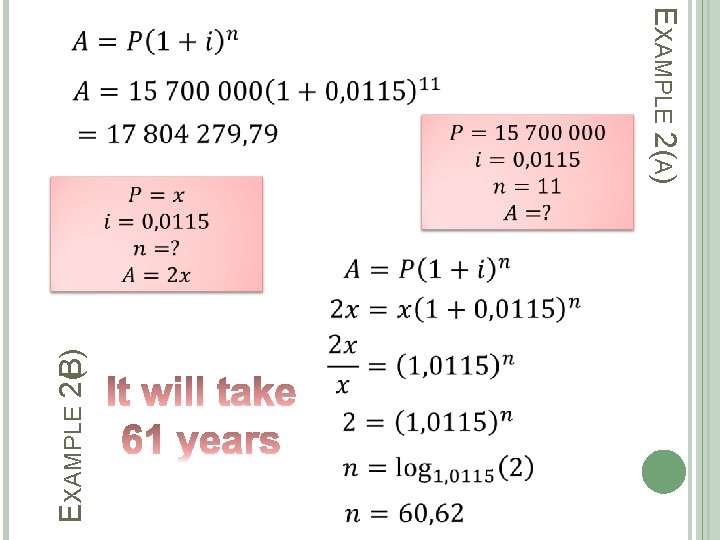








- Slides: 60

FINANCIAL MATHS Grade 12 Paper I


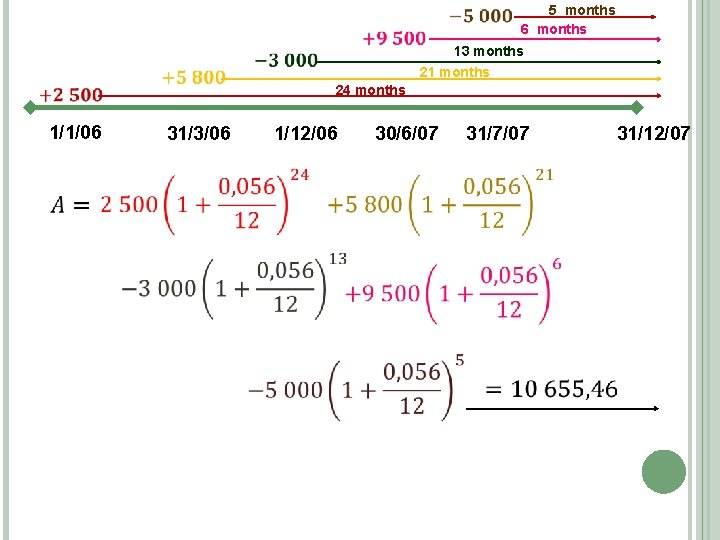
1/1/06 T 0 31/3/06 1/12/06 30/6/07 31/7/07 31/12/0 7 T 2 THE FOLLOWING TRANSACTIONS TOOK PLACE: 1 JANUARY 2006 – DEPOSIT R 2 500 END OF MARCH – DEPOSITR 5 800 1 DECEMBER 2006 – WITHDRAWAL R 3 000 END OF JUNE 2007 – DEPOSIT R 9 500 ONE MONTH LATER – WITHDRAWALR 5 000 CALCULATE THE BALANCE ON 31 DECEMBER 2007 IF INTEREST IS CALCULATED AT 5, 6% PA COMPOUNDED MONTHLY.

5 months 6 months 1/1/06 13 months 21 months 24 months 31/3/06 1/12/06 30/6/07 31/7/07 31/12/07

ANNUITIES Lesson 2

ANNUITIES An annuity is a number of equal payments made at regular intervals, earning interest. Future value Annuities Savings, investments and sinking funds. Present value Annuities Loans

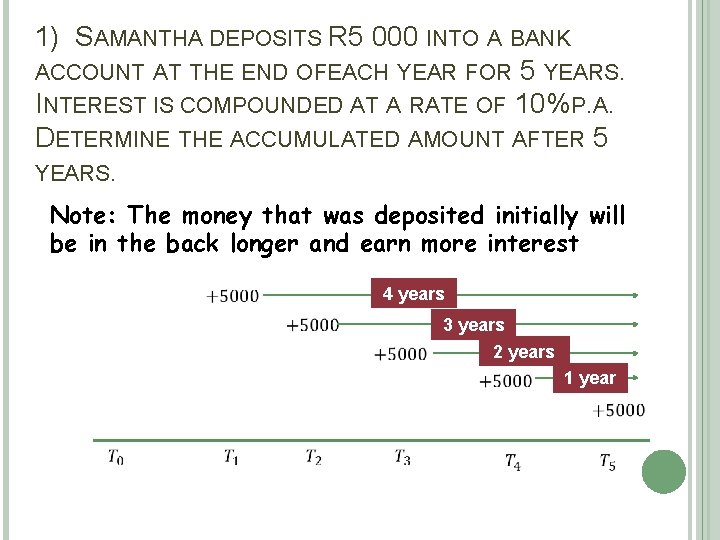
1) SAMANTHA DEPOSITS R 5 000 INTO A BANK ACCOUNT AT THE END OFE ACH YEAR FOR 5 YEARS. INTEREST IS COMPOUNDED AT A RATE OF 10%P. A. DETERMINE THE ACCUMULATED AMOUNT AFTER 5 YEARS. Note: The money that was deposited initially will be in the back longer and earn more interest 4 years 3 years 2 years 1 year

Simplify and rearrange: This is a geometric series:

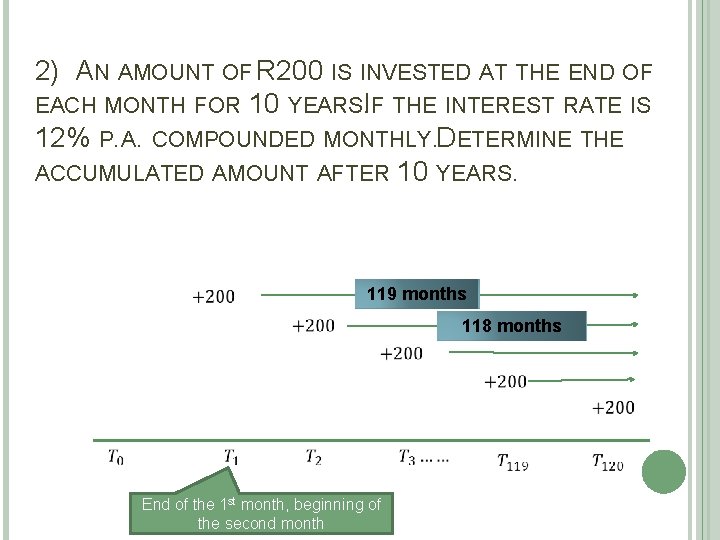
2) AN AMOUNT OF R 200 IS INVESTED AT THE END OF EACH MONTH FOR 10 YEARSI. F THE INTEREST RATE IS 12% P. A. COMPOUNDED MONTHLY. DETERMINE THE ACCUMULATED AMOUNT AFTER 10 YEARS. 119 months 118 months End of the 1 st month, beginning of the second month

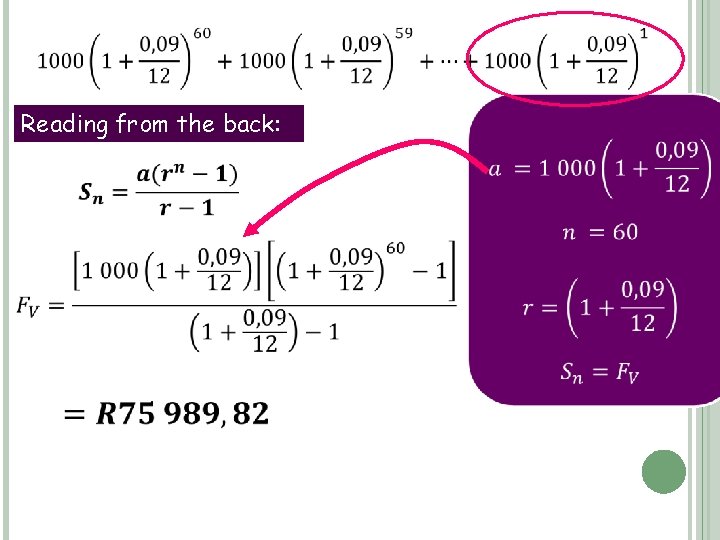
Reading from the back:

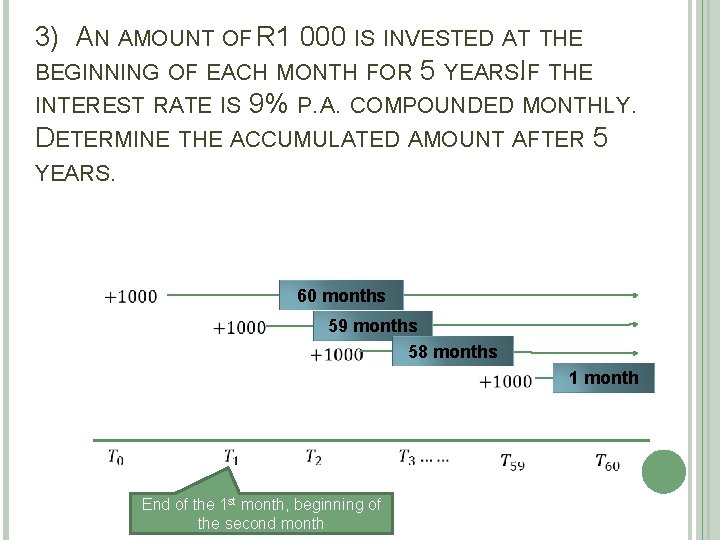
3) AN AMOUNT OF R 1 000 IS INVESTED AT THE BEGINNING OF EACH MONTH FOR 5 YEARSI. F THE INTEREST RATE IS 9% P. A. COMPOUNDED MONTHLY. DETERMINE THE ACCUMULATED AMOUNT AFTER 5 YEARS. 60 months 59 months 58 months 1 month End of the 1 st month, beginning of the second month

Reading from the back:

FUTURE VALUE ANNUITIES - FORMULA Lesson 3

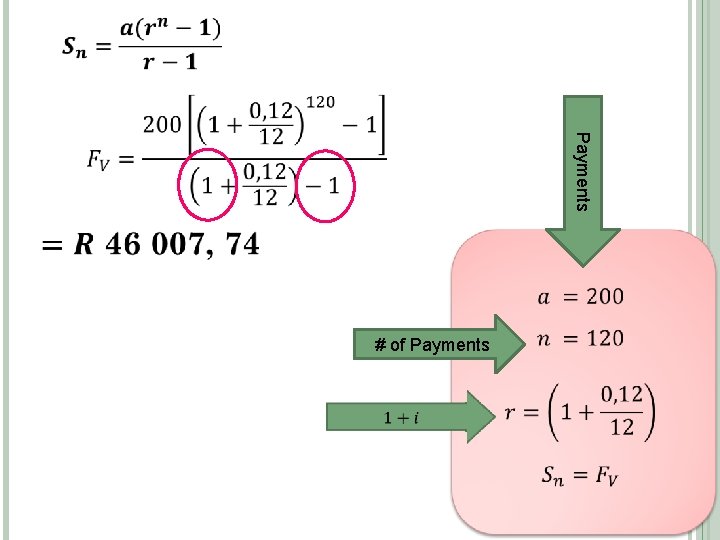
Payments # of Payments

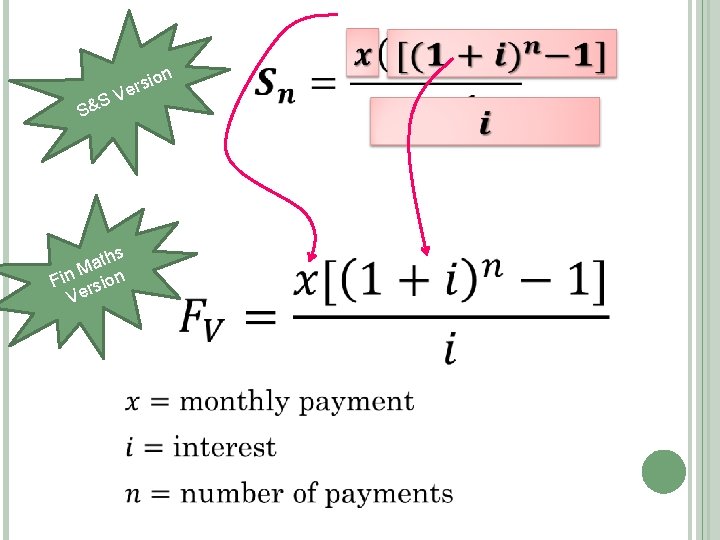
sio r e V S S& ths a M Fin rsion Ve n

1) AN INVESTMENT OF R 300 PER MONTH, WITH THE FIRST PAYMENT MADE IN A MONTH’S TIME, AT 18% PA COMPOUNDED MONTHLY. CALCULATE HOW MUCH THE INVESTMENT WILL BE WORTH IN 3 YEARS TIME. = R 14 182, 79

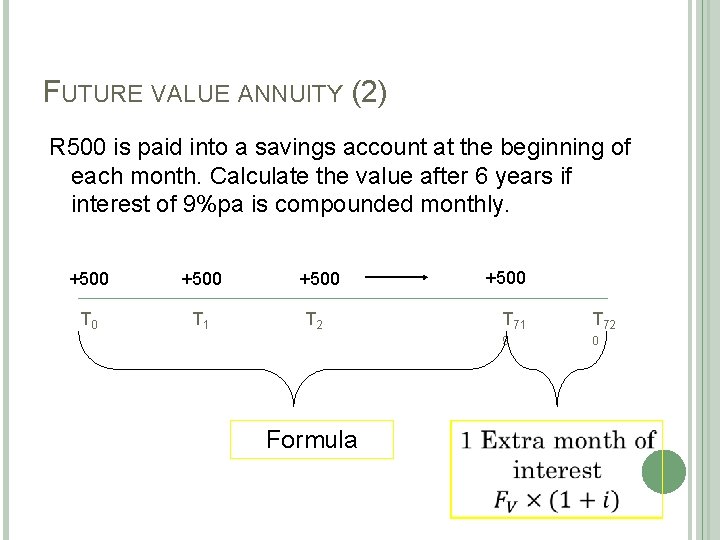
FUTURE VALUE ANNUITY (2) R 500 is paid into a savings account at the beginning of each month. Calculate the value after 6 years if interest of 9%pa is compounded monthly. +500 T 0 T 1 +500 T 2 Formula T 71 T 72 9 0
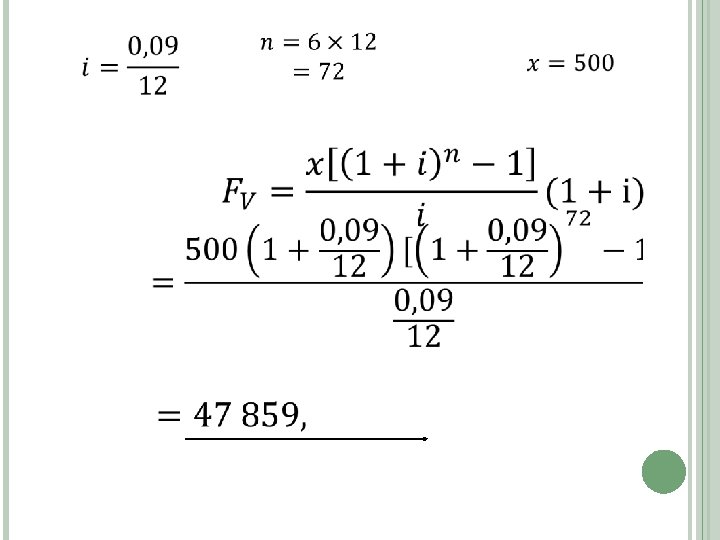

3) HOW MUCH MONEY MUST BE INVESTED AT THE END OF EACH MONTH IN ANNUITY TO REALISE R 1 000 IN 20 YEAR’S TIME IF THE INTEREST RATE IS 9% PA COMPOUNDED MONTHLY? = R 1 497, 26

MORE CHALLENGING FUTURE VALUE ANNUITIES Lesson 4

VOCABULARY Book value: Value after depreciation has been taken into account. Scrap value: The book value of an asset at the end of its useful life. Sinking fund: Fund set up to replace an asset at the end of its useful life.

EXAMPLE 1 Machinery is purchased at a cost of R 550 000 and is expected to rise in cost at 15% per annum, compound interest, and depreciate in value at a rate of 8% per annum compounded annually. A sinking fund is started to make provision for replacing the old machine. The sinking fund pays 16% per annum compounded monthly, and you make monthly payments into this account for 10 years, starting immediately and ending one month before the purchase of the new machine. Determine: 1. the replacement cost of a new machine ten years from now 2. the scrap value of the machine in ten years time. 3. the monthly payment into the sinking fund that will make provision for the replacement of the new machine.

1 A) REPLACEMENT COST (INFLATION) P = 550 000 i = 0, 15 n = 10 A = ? Compound interest

1 B) SCRAP VALUE (DEPRECIATION) P = 550 000 i = 0, 08 n = 10 A = ? Compound interest

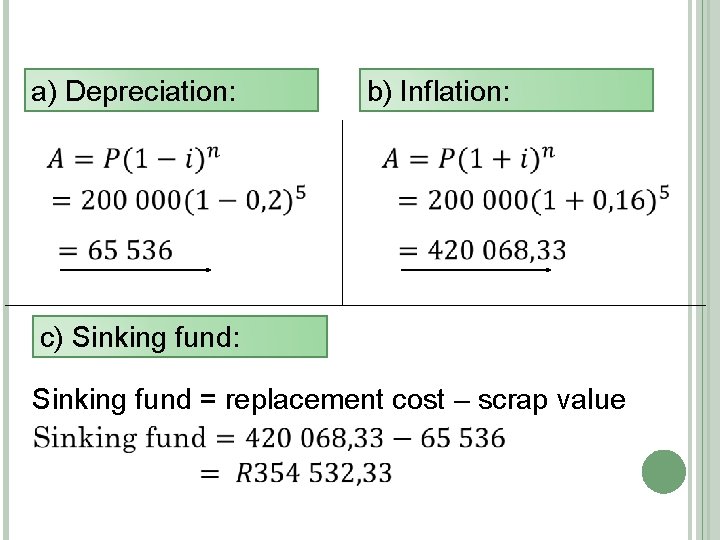
1 C) SINKING FUND (ANNUITY) Sinking fund = replacement cost – scrap value Sinking fund = 2 225056, 76 – 238 913, 65 = R 1 986 143, 11

EXAMPLE 2 A small business purchase a photocopying machine for R 200 000. The photocopier depreciates in value at 20% p. a. on a reducing balance. The business wants to buy a new machine in 5 years time. A new machine will cost much more in the future and its cost will escalate at 16% p. a. effective. The old machine will be sold at scrap value after 5 years. A sinking fund is set up immediately in order to safe up for the new machine. The proceeds of the sale of the old machine will be used together with the sinking fund to buy the new machine. The business will pay equal monthly amounts into the sinking fund and interest rate is 18% p. a. compounded monthly. The first payment will be made immediately and the last payment will be made at the end of the 5 year period.

EXAMPLE 2 a) b) c) d) Find the scrap value of the old machine. Calculate the cost of the new machine in 5 years time. Determine the amount required in the sinking fund, to be able to buy the new machine. Calculate the monthly payments that the business needs to make into the sinking fund.

a) Depreciation: b) Inflation: c) Sinking fund: Sinking fund = replacement cost – scrap value

D) MONTHLY PAYMENTS

PRESENT VALUE ANNUITIES Lesson 5

PRESENT VALUE ANNUITY Loans ⇒ principal is getting smaller, the longer you have been paying. You always pay a loan at the end of the month. Present value is the amount at the beginning of the loan.
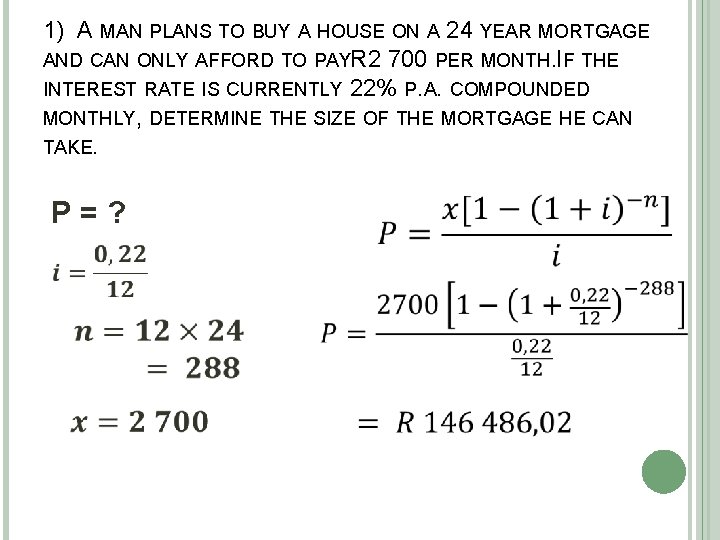
1) A MAN PLANS TO BUY A HOUSE ON A 24 YEAR MORTGAGE AND CAN ONLY AFFORD TO PAYR 2 700 PER MONTH. IF THE INTEREST RATE IS CURRENTLY 22% P. A. COMPOUNDED MONTHLY, DETERMINE THE SIZE OF THE MORTGAGE HE CAN TAKE. P = ?

2) YOU PLAN TO BUY A HOUSE ON A 20 YEAR MORTGAGE WITH MONTHLY REPAYMENTS OF R 3 300 AND A DEPOSIT OF R 50 000. IF THE INTEREST RATE IS CURRENTLY 17% P. A. COMPOUNDED MONTHLY. WHAT IS THE PRICE OF THE HOUSE? P = ? Loan : Price of the house
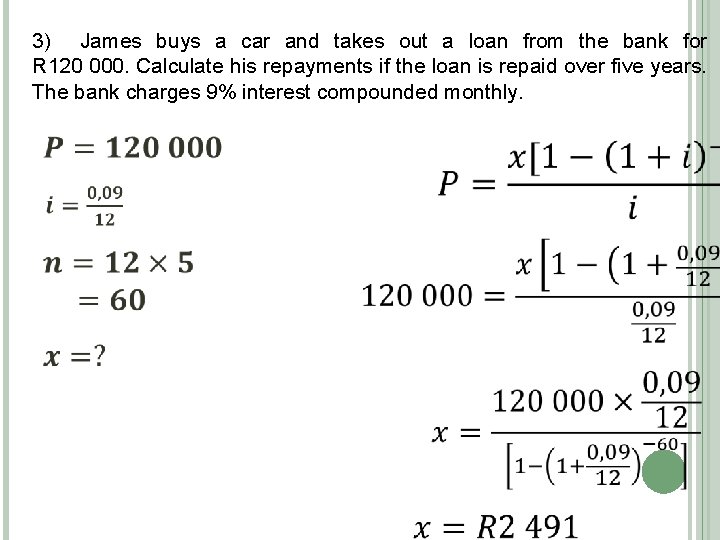
3) James buys a car and takes out a loan from the bank for R 120 000. Calculate his repayments if the loan is repaid over five years. The bank charges 9% interest compounded monthly.

4) SANDRA BUYS A SLIMMING MACHINE AND PAYS A DEPOSIT OF R 2 000. THE BALANCE IS PAID OFF BY 36 MONTHLY INSTALMENTS OF R 1 800. INTEREST IS CALCULATED @ 23%P. A. COMPOUNDED MONTHLY. How much would she have saved if she paid cash: Calculate the purchase price of the machine: Amount she paid:

PRESENT VALUE FORMULA – OUTSTANDING BALANCE Lesson 6

OUTSTANDING BALANCE When you want to settle a loan, or change the interest rate you need to calculate the outstanding balance.

EXAMPLE 1 A car is bought for R 180 000. 10% is paid in cash and the balance is borrowed at an interest rate of 10, 5% pa compounded monthly. Loan is repaid over 6 years Determine the monthly repayments Determine the balance on the loan at the end of 2 years.

A) MONTHLY REPAYMENTS

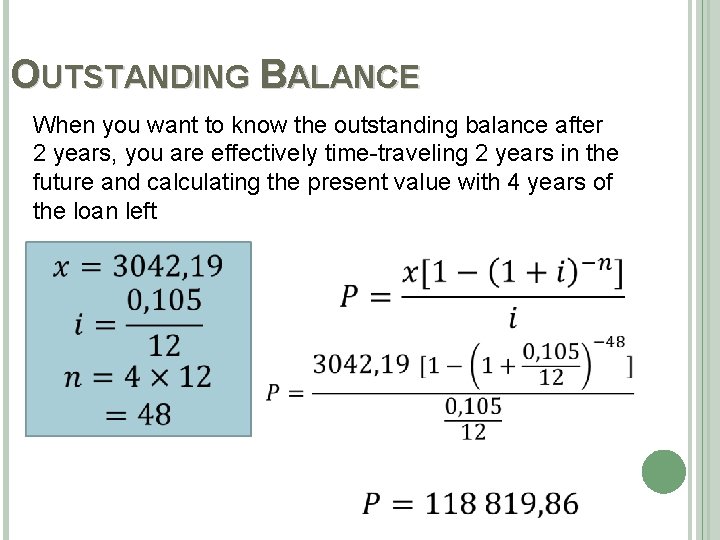
OUTSTANDING BALANCE When you want to know the outstanding balance after 2 years, you are effectively time-traveling 2 years in the future and calculating the present value with 4 years of the loan left

EXAMPLE 2 Trevor purchases a house for R 780 000 on a mortgage of 20 years with interest at 17% pa compounded monthly. a) Calculate the outstanding balance after 8 years. b) Calculate the new monthly payments if the interest rate should change to 19%pa compounded monthly after 8 years.

A) MONTHLY REPAYMENTS

OUTSTANDING BALANCE After making payments for 8 years, there is 12 years of payments left.

B) NEW MONTHLY REPAYMENTS

Lesson 7 & 8

EXAMPLE 1

It would take 93 months to double the money EXAMPLE 1

EXAMPLE 2
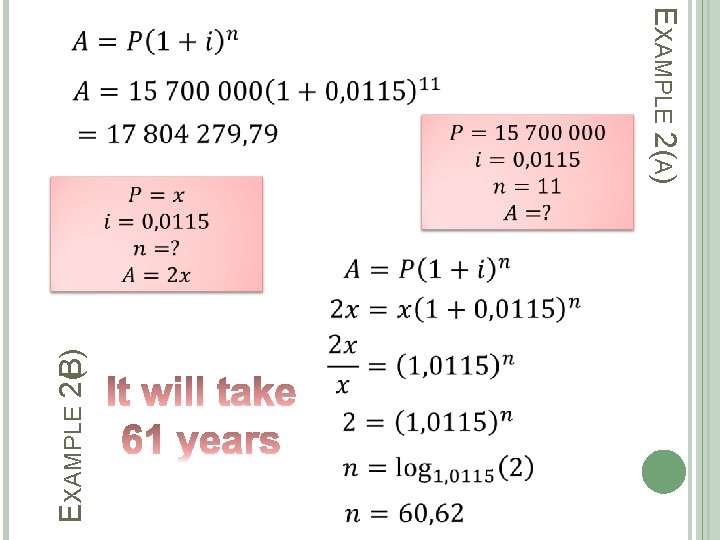
EXAMPLE 2(B) EXAMPLE 2(A)

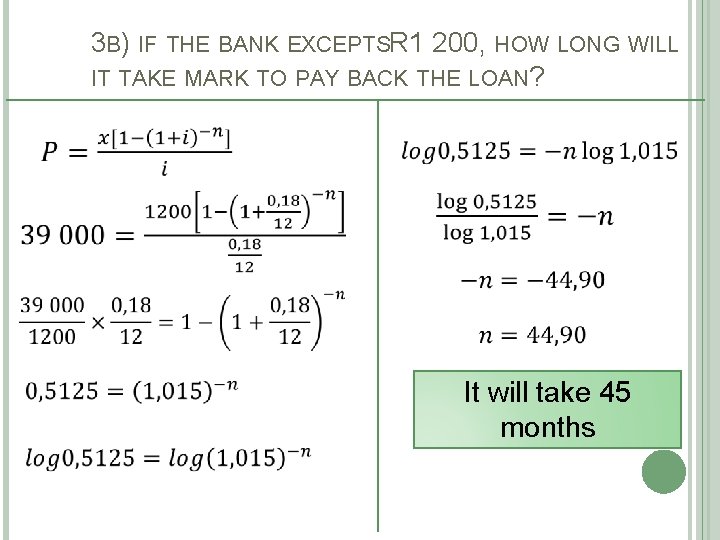
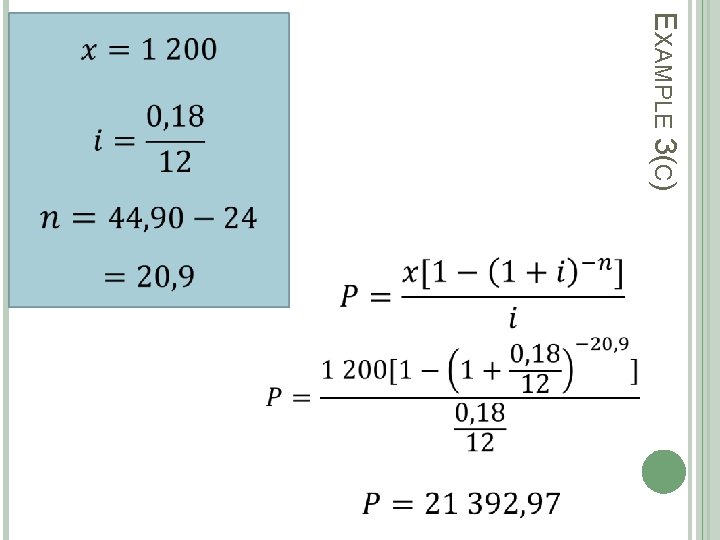
EXAMPLE 3 Mark wants to purchase a big screen television set at a cash price of R 39 000. He wishes to obtain a loan from the bank at an interest rate of 18% p. a. compounded monthly. Mark can only afford to pay R 1 200 per month for a period of 36 months. a) Will the bank give him a loan based on this information? b) If the bank agrees to accept R 1 200 per month, how long will it take Mark to pay back the loan? c) What is the outstanding amount on the loan after 2 years?

3 A) WILL THE BANK GIVE HIM A LOAN BASED ON THIS INFORMATION? Paying R 1 200 per month for 36 months does not settle a R 39 000 loan.

3 B) IF THE BANK EXCEPTSR 1 200, HOW LONG WILL IT TAKE MARK TO PAY BACK THE LOAN? It will take 45 months

EXAMPLE 3(C)

EXAMPLE 4

EXAMPLE 4(A) It will take 38 months

EXAMPLE 4(B) To determine the last payment we need to calculate the outstanding balance after making 37 payments.

DEFERRED ANNUITY Lesson 9

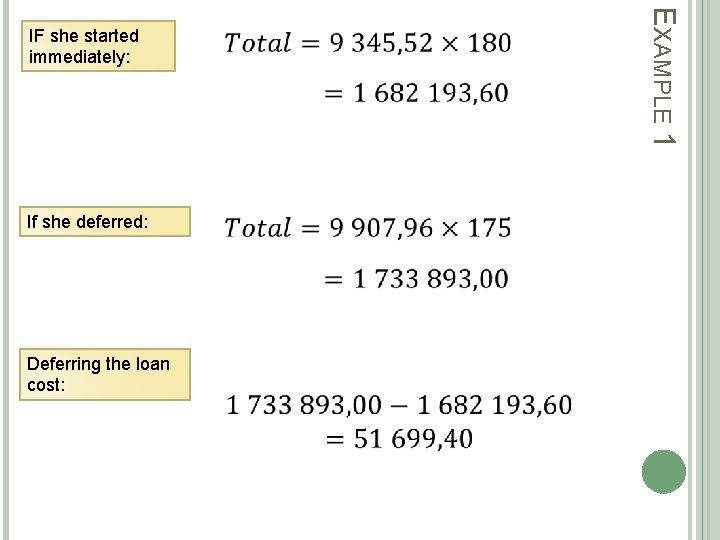
EXAMPLE 1

Next 175 months: EXAMPLE 1 First 5 months:

If she deferred: Deferring the loan cost: EXAMPLE 1 IF she started immediately: