Financial Engineering Interest Rates and Fixed Income Securities

Financial Engineering Interest Rates and Fixed Income Securities Zvi Wiener mswiener@mscc. huji. ac. il tel: 02 -588 -3049 Zvi Wiener Cont. Time. Fin - 6 1

Bonds A bond is a contract, paid up-front that yields a known amount at a known date (maturity). The bond may pay a dividend (coupon) at fixed times during the life. Additional options: callable, puttable, indexed, prepayment options, etc. Credit risk, recovery ratio, rating. Zvi Wiener Cont. Time. Fin - 6 2

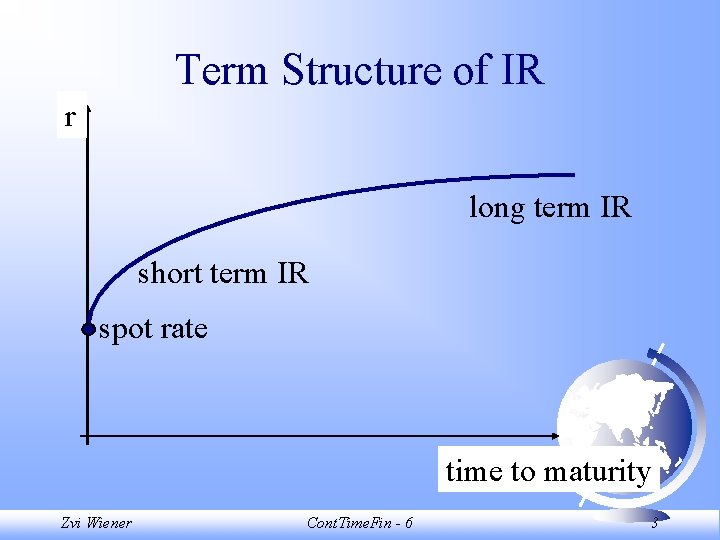
Term Structure of IR r long term IR short term IR spot rate time to maturity Zvi Wiener Cont. Time. Fin - 6 3

Known IR V - value of a contract. r(t) - short term interest rate. If there is no risk and no coupons then d. V = r. Vdt V(t) = V(T)e-rt if there is a continuous dividend stream d. V+c. Vdt = r. Vdt Zvi Wiener Cont. Time. Fin - 6 4

Known IR If r is not constant, but not risky r(t) d. V = r(t)Vdt If there is a continuous dividend stream d. V+c(t)Vdt = r(t)Vdt Zvi Wiener Cont. Time. Fin - 6 5

Known IR Assume that there are zero coupon bonds for all possible ttm (time to maturity). Denote the price of these bonds by V(t, T). Zvi Wiener Cont. Time. Fin - 6 6

Known IR Zvi Wiener Cont. Time. Fin - 6 7

Yield Zvi Wiener Cont. Time. Fin - 6 8

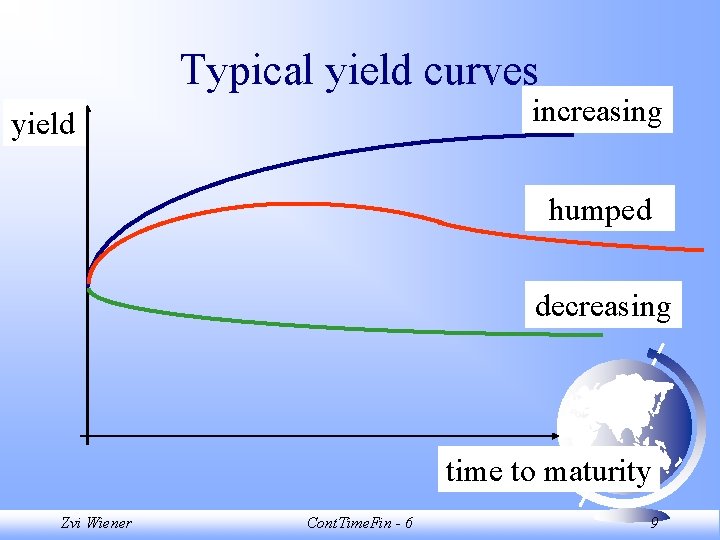
Typical yield curves increasing yield humped decreasing time to maturity Zvi Wiener Cont. Time. Fin - 6 9

Typical yield curves F increasing - the most typical. decreasing - short rates are high but expected to fall. F humped - short rates are expected to fall soon. F Zvi Wiener Cont. Time. Fin - 6 10

Term Structure Explanations Expectation hypothesis states F 0=E(PT) this hypothesis is be true if all market participants were risk neutral. Zvi Wiener Cont. Time. Fin - 6 11

Term Structure Explanations Normal Backwardation (Keynes), commodities are used by hedgers to reduce risk. In order to induce speculators to take the opposite positions, the producers must offer a higher return. Thus speculators enter the long side and have the expected profit of E(PT) – F 0 > 0 Zvi Wiener Cont. Time. Fin - 6 12

Term Structure Explanations Contango is similar to the normal backwardation, but the natural hedgers are the purchasers of a commodity, rather than suppliers. Since speculators must be paid for taking risk, the opposite relation holds: E(PT) – F 0 < 0 Zvi Wiener Cont. Time. Fin - 6 13

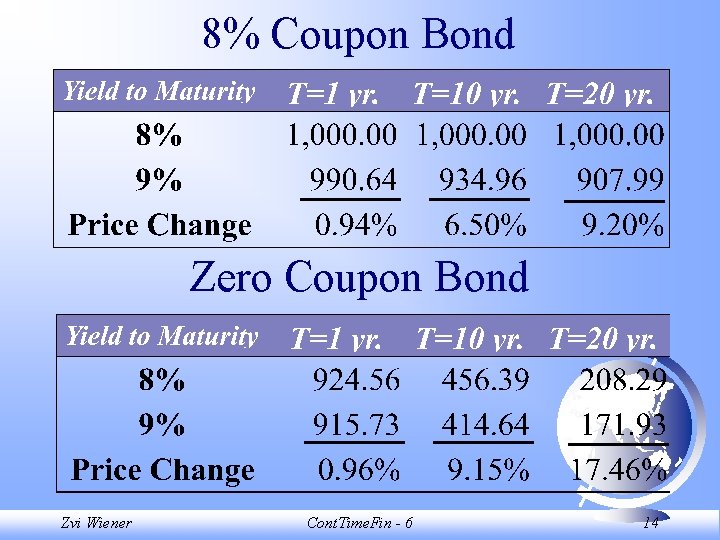
8% Coupon Bond Zero Coupon Bond Zvi Wiener Cont. Time. Fin - 6 14

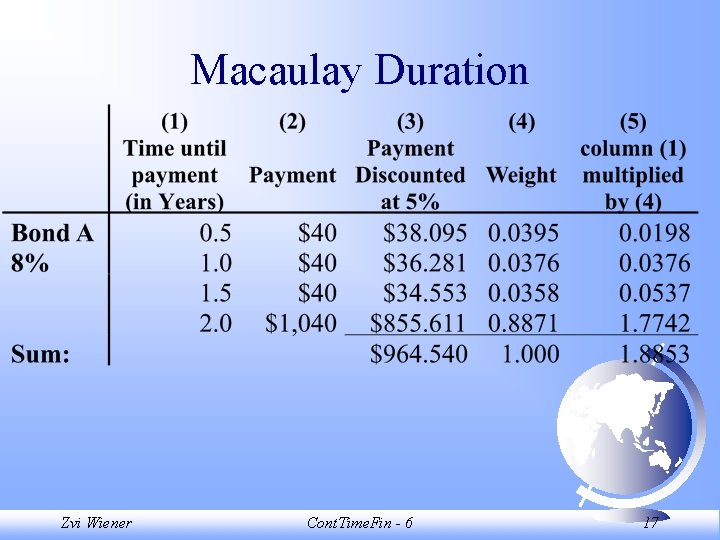
Duration F. Macaulay (1938) Better measurement than time to maturity. Weighted average of all coupons with the corresponding time to payment. Bond Price = Sum[ CFt/(1+y)t ] suggested weight of each coupon: wt = CFt/(1+y)t /Bond Price What is the sum of all wt? Zvi Wiener Cont. Time. Fin - 6 15

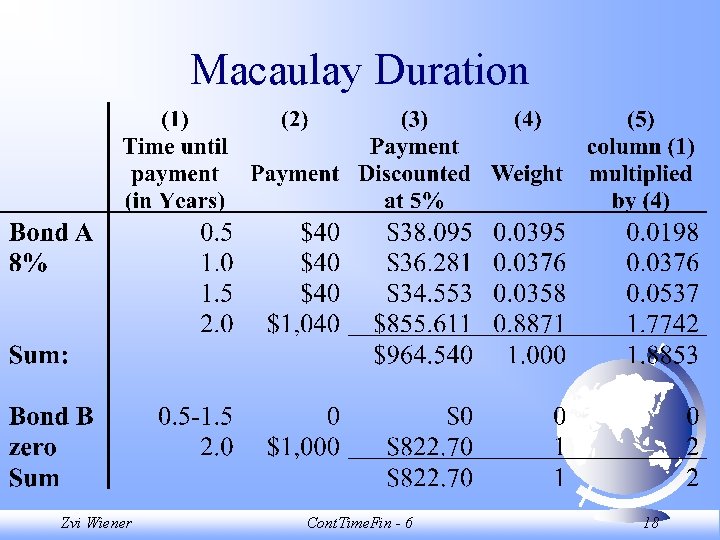
Macaulay Duration A weighted sum of times to maturities of each coupon. What is the duration of a zero coupon bond? Zvi Wiener Cont. Time. Fin - 6 16

Macaulay Duration Zvi Wiener Cont. Time. Fin - 6 17

Macaulay Duration Zvi Wiener Cont. Time. Fin - 6 18

Duration Sensitivity to IR changes: Long term bonds are more sensitive. F Lower coupon bonds are more sensitive. F The sensitivity depends on levels of IR. F Zvi Wiener Cont. Time. Fin - 6 19

Duration The bond price volatility is proportional to the bond’s duration. Thus duration is a natural measure of interest rate risk exposure. Zvi Wiener Cont. Time. Fin - 6 20

Modified Duration The percentage change in bond price is the product of modified duration and the change in the bond’s yield to maturity. Zvi Wiener Cont. Time. Fin - 6 21

Comparison of two bonds Coupon bond with duration Zero-coupon bond with equal 1. 8853 duration must have 1. 8853 years to maturity. At 5% semiannual its price is Price (at 5% for 6 m. ) is $964. 5405 ($1, 000/1. 053. 7706)=$831. 9623 If IR increase by 1 bp If IR increase to 5. 01%, the price becomes: (to 5. 01%), its price will fall to $964. 1942, or ($1, 000/1. 05013. 7706)=$831. 66 0. 359% decline. Zvi Wiener Cont. Time. Fin - 6 22

Duration D Zero coupon bond 15% coupon, YTM = 15% Maturity 0 Zvi Wiener 3 m 6 m 1 yr 3 yr Cont. Time. Fin - 6 5 yr 10 yr 30 yr 23

Example A bond with 30 -yr to maturity Coupon 8%; paid semiannually YTM = 9% P 0 = $897. 26 D = 11. 37 Yrs if YTM = 9. 1%, what will be the price? Zvi Wiener Cont. Time. Fin - 6 24

Example A bond with 30 -yr to maturity Coupon 8%; paid semiannually YTM = 9% P 0 = $897. 26 D = 11. 37 Yrs if YTM = 9. 1%, what will be the price? P/P = - y D* P = -( y D*)P = -$9. 36 P = $897. 26 - $9. 36 = $887. 90 Zvi Wiener Cont. Time. Fin - 6 25

What Determines Duration? Duration of a zero-coupon bond equals maturity. F Holding ttm constant, duration is higher when coupons are lower. FHolding other factors constant, duration is higher when ytm is lower. F Duration of a perpetuity is (1+y)/y. F Zvi Wiener Cont. Time. Fin - 6 26

What Determines Duration? Holding the coupon rate constant, duration not always increases with ttm. F Zvi Wiener Cont. Time. Fin - 6 27

Duration Zvi Wiener Cont. Time. Fin - 6 28

Zvi Wiener Cont. Time. Fin - 6 29

Zvi Wiener Cont. Time. Fin - 6 30

Zvi Wiener Cont. Time. Fin - 6 31

Modern Approach Duration can be regarded as the discount-rate elasticity of the bond price Zvi Wiener Cont. Time. Fin - 6 32

Modern Approach Duration can be used to measure the price volatility of a bond: Zvi Wiener Cont. Time. Fin - 6 33

Modern Approach What are the natural bounds on duration? Can duration be bigger than maturity? Can duration be negative? How to measure duration of a portfolio? Zvi Wiener Cont. Time. Fin - 6 34

Duration: Modern Approach Zvi Wiener Cont. Time. Fin - 6 35

Duration of a Portfolio Zvi Wiener Cont. Time. Fin - 6 36

Duration of a Portfolio Zvi Wiener Cont. Time. Fin - 6 37

Modern Approach to Duration Simon Benninga, Financial Modelling, the MIT press, Cambridge, MA, ISBN 0 -262 -02437 -3, $45 MIT Press tel: 800 -356 -0343 http: //mitpress. mit. edu/book-home. tcl? isbn=0262024373 see also my advanced lecture notes on duration Convexity is a similar measurement but with second derivative. Zvi Wiener Cont. Time. Fin - 6 38

Financial Modelling by Simon Benninga Implementation in Excel F Duration Patterns F Duration of a bond with uneven payments F Calculating YTM for uneven periods F Nonflat term structure and duration F Immunization strategies F Cheapest to deliver option and Duration F Zvi Wiener Cont. Time. Fin - 6 39

Passive Bond Management Passive management takes bond prices as fairly set and seeks to control only the risk of the fixed-income portfolio. F Indexing strategy – attempts to replicate a bond index F Immunization – used to tailor the risk to specific needs (insurance companies, pension funds) Zvi Wiener Cont. Time. Fin - 6 40

Bond-Index Funds Similar to stock indexing. Major indices: Lehman Brothers, Merill Lynch, Salomon Brothers. Include: government, corporate, mortgagebacked, Yankee bonds (dollar denominated, SEC registered bonds of foreign issuers, sold in the US). Zvi Wiener Cont. Time. Fin - 6 41

Bond-Index Funds Properties: many issues not all are liquid replacement of maturing issues Tracking error is a good measurement of performance. According to Salomon Bros. With $100 M one can track the index within 4 bp. tracking error per month. Zvi Wiener Cont. Time. Fin - 6 42

Cellular approach Zvi Wiener Cont. Time. Fin - 6 43

Immunization techniques refer to strategies used by investors to shield their overall financial status from exposure to interest rate fluctuations. Zvi Wiener Cont. Time. Fin - 6 44

Net Worth Immunization Banks and thrifts have a natural mismatch between assets and liabilities. Liabilities are primarily short-term deposits (low duration), assets are typically loans or mortgages (higher duration). When will banks lose money, when IR increase or decline? Zvi Wiener Cont. Time. Fin - 6 45

Gap Management ARM are used to reduce duration of bank portfolios. Other derivative securities can be used. Capital requirement on duration (exposure). Basic idea: to match duration of assets and liabilities. Zvi Wiener Cont. Time. Fin - 6 46

Target Date Immunization Important for pension funds and insurances. Price risk and reinvestment risk. What is the correlation between them? Zvi Wiener Cont. Time. Fin - 6 47

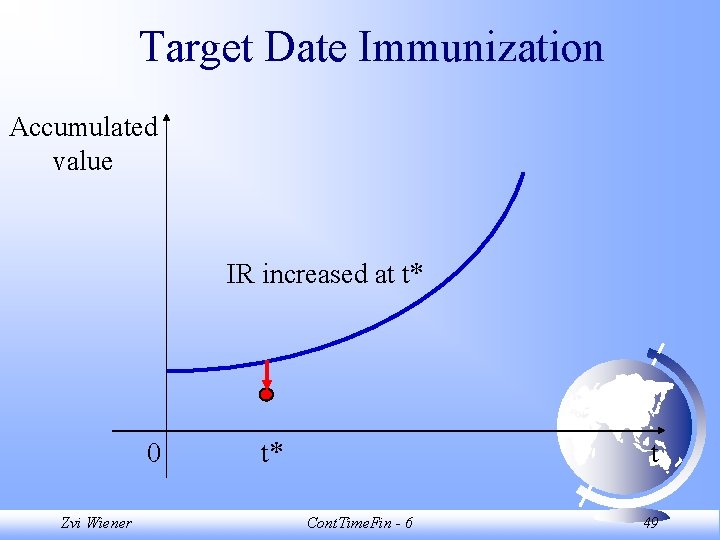
Target Date Immunization Accumulated value Original plan 0 Zvi Wiener t* t Cont. Time. Fin - 6 48

Target Date Immunization Accumulated value IR increased at t* 0 Zvi Wiener t* t Cont. Time. Fin - 6 49

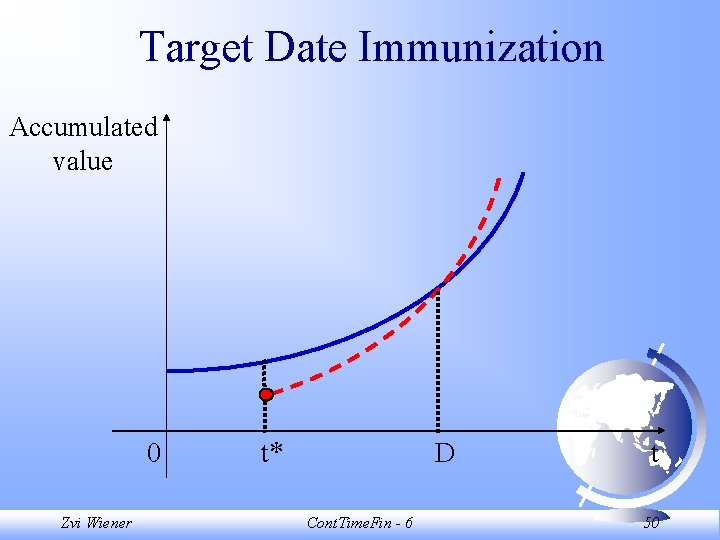
Target Date Immunization Accumulated value 0 Zvi Wiener t* D Cont. Time. Fin - 6 t 50

Target Date Immunization Accumulated value 0 Zvi Wiener Continuous rebalancing can keep the terminal value unchanged t* D Cont. Time. Fin - 6 t 51

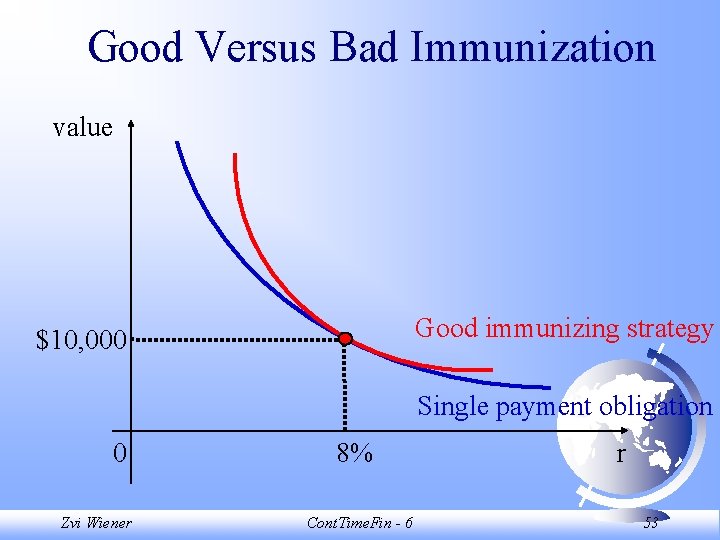
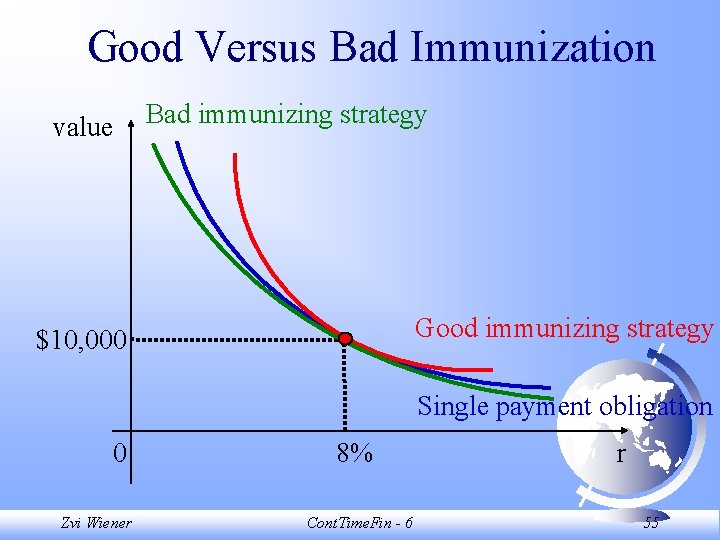
Good Versus Bad Immunization value $10, 000 Single payment obligation 0 Zvi Wiener 8% Cont. Time. Fin - 6 r 52

Good Versus Bad Immunization value Good immunizing strategy $10, 000 Single payment obligation 0 Zvi Wiener 8% Cont. Time. Fin - 6 r 53

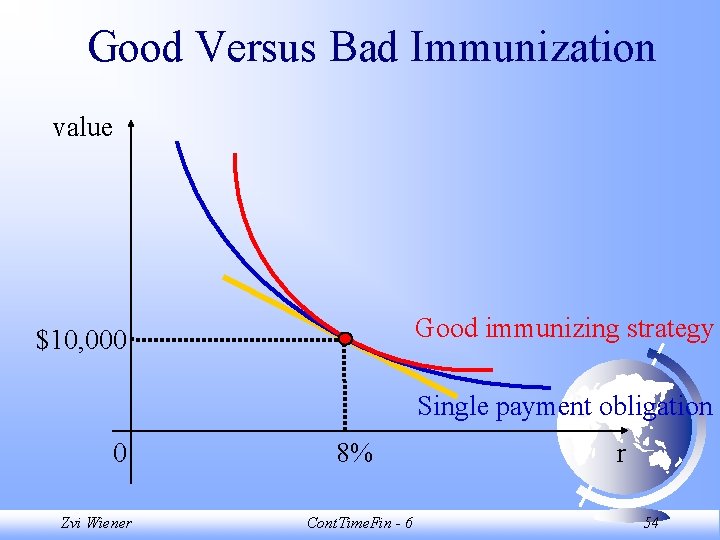
Good Versus Bad Immunization value Good immunizing strategy $10, 000 Single payment obligation 0 Zvi Wiener 8% Cont. Time. Fin - 6 r 54

Good Versus Bad Immunization value Bad immunizing strategy Good immunizing strategy $10, 000 Single payment obligation 0 Zvi Wiener 8% Cont. Time. Fin - 6 r 55

Standard Immunization Is very useful but is based on the assumption of the flat term structure. Often a higher order immunization is used (convexity, etc. ). Another reason for goal oriented mutual funds (retirement, education, housing, medical expenses). Zvi Wiener Cont. Time. Fin - 6 56

Duration Immunization Duration protects against small IR changes. F Duration assumes a parallel change in the TS. F Immunization is based on nominal IR. F Immunization is very conservative and is inappropriate for many portfolio managers. F The passage of time changes both duration and horizon date, one need to rebalance. F Duration changes if yields change. F Obtaining bonds for immunization can be difficult. F Zvi Wiener Cont. Time. Fin - 6 57

Cash Flow Matching and Dedication Is a very reasonable strategy, but not always realizable. Uncertainty of payments. Lack of perfect match Saving on transaction fees. Zvi Wiener Cont. Time. Fin - 6 58

Active Bond Management Mainly speculative approach based on ability to predict IR or credit enhancement or market imperfections (identifying mispriced loans). Zvi Wiener Cont. Time. Fin - 6 59

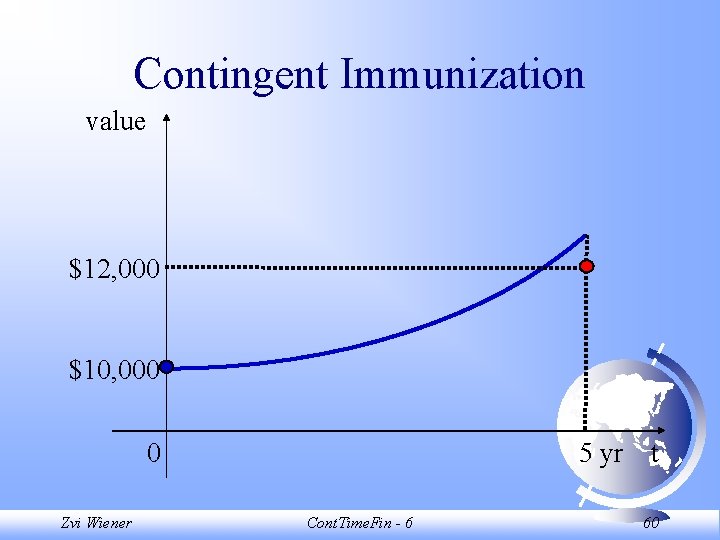
Contingent Immunization value $12, 000 $10, 000 0 Zvi Wiener 5 yr t Cont. Time. Fin - 6 60

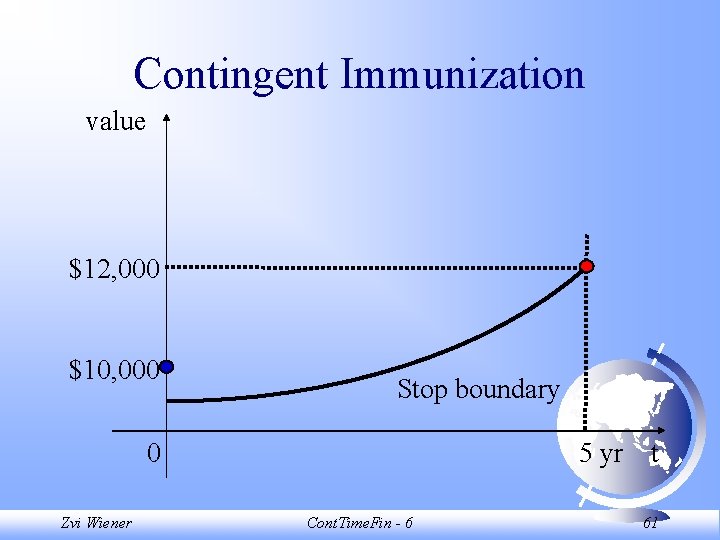
Contingent Immunization value $12, 000 $10, 000 Stop boundary 0 Zvi Wiener 5 yr t Cont. Time. Fin - 6 61

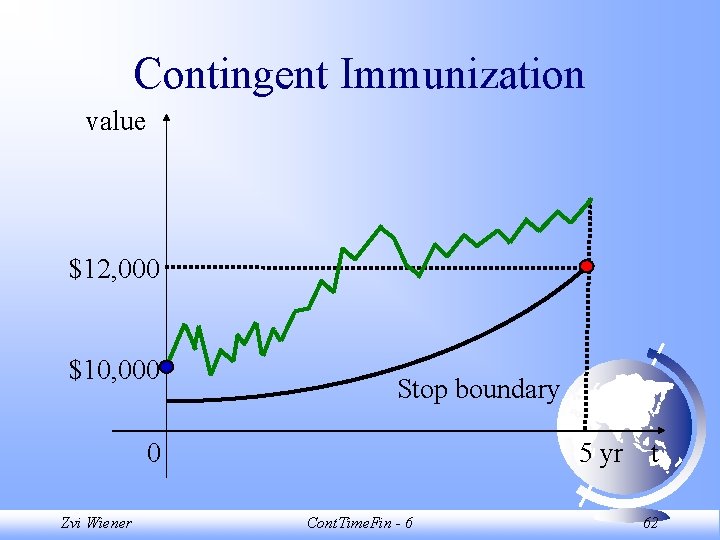
Contingent Immunization value $12, 000 $10, 000 Stop boundary 0 Zvi Wiener 5 yr t Cont. Time. Fin - 6 62

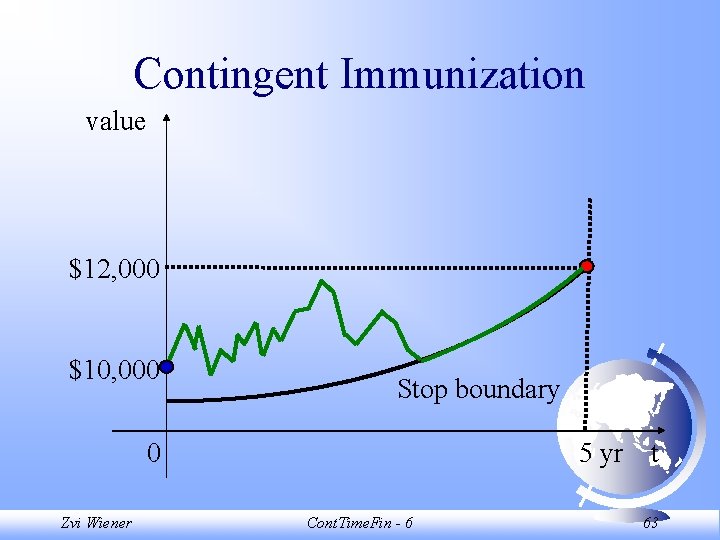
Contingent Immunization value $12, 000 $10, 000 Stop boundary 0 Zvi Wiener 5 yr t Cont. Time. Fin - 6 63

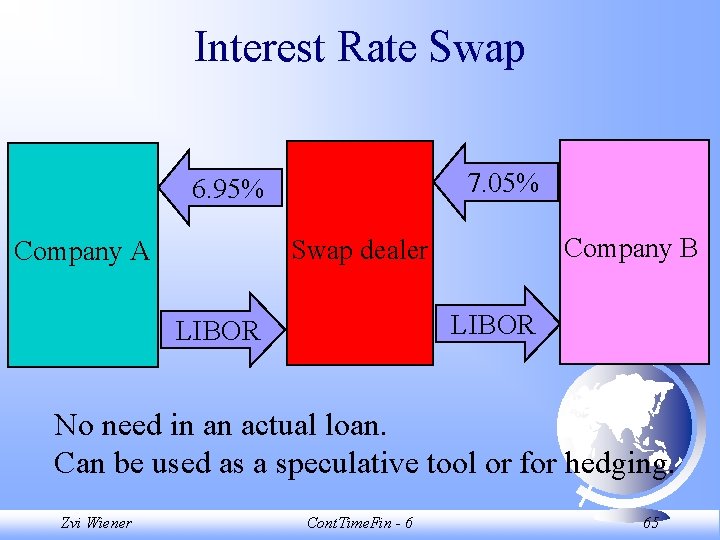
Interest Rate Swap One of the major fixed-income tools. Example: 6 m LIBOR versus 7% fixed. Exchange of net cash flows. Risk involved: IR risk, default risk (small). Why the default risk on IR swaps is small? Zvi Wiener Cont. Time. Fin - 6 64

Interest Rate Swap 7. 05% 6. 95% Company B Swap dealer Company A LIBOR No need in an actual loan. Can be used as a speculative tool or for hedging. Zvi Wiener Cont. Time. Fin - 6 65

Interest Rate Swap Can not be priced as an exchange of two loans (old method). Why? Zvi Wiener Cont. Time. Fin - 6 66

Currency Swap A similar exchange of two loans in different currencies. Subject to a higher default risk, because of the principal. Is useful for international companies to hedge currency risk. Zvi Wiener Cont. Time. Fin - 6 67

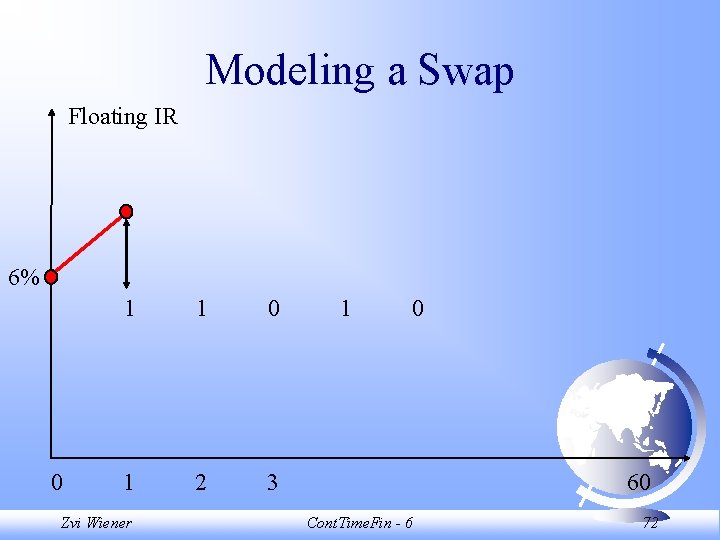
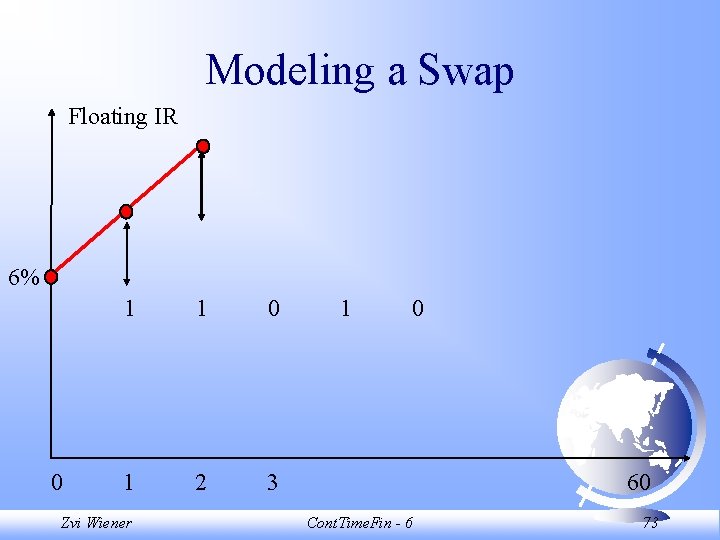
Modeling a Swap A simple fixed versus floating swap. Current fixed rate on a 30 years loan is 7% with semi annual payments for simplicity. Current floating rate is 6%. Notional amount is 1, 000. How can we model our future payments? Zvi Wiener Cont. Time. Fin - 6 68

Modeling a Swap There are two flows of cash. At maturity they cancel each other. The fixed part has payments known in advance. The only uncertainty is with the floating part. We need a simple model of interest rates. Zvi Wiener Cont. Time. Fin - 6 69

Modeling a Swap Floating IR 6% 0 1 Zvi Wiener 2 3 60 Cont. Time. Fin - 6 70

Modeling a Swap Floating IR 6% 0 1 1 0 1 2 3 Zvi Wiener 1 0 60 Cont. Time. Fin - 6 71

Modeling a Swap Floating IR 6% 0 1 1 0 1 2 3 Zvi Wiener 1 0 60 Cont. Time. Fin - 6 72

Modeling a Swap Floating IR 6% 0 1 1 0 1 2 3 Zvi Wiener 1 0 60 Cont. Time. Fin - 6 73

Modeling a Swap Floating IR 6% 0 1 1 0 1 2 3 Zvi Wiener 1 0 60 Cont. Time. Fin - 6 74

Modeling a Swap Floating IR 6% 0 1 1 0 1 2 3 Zvi Wiener 1 0 60 Cont. Time. Fin - 6 75

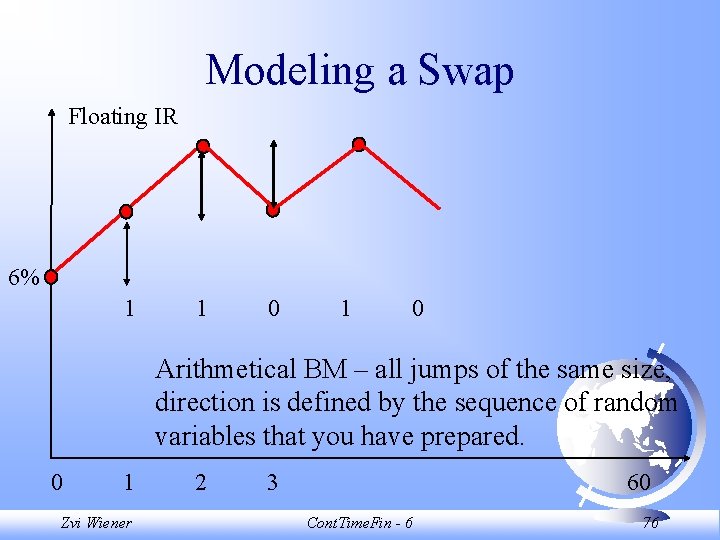
Modeling a Swap Floating IR 6% 1 1 0 Arithmetical BM – all jumps of the same size, direction is defined by the sequence of random variables that you have prepared. 0 1 Zvi Wiener 2 3 60 Cont. Time. Fin - 6 76

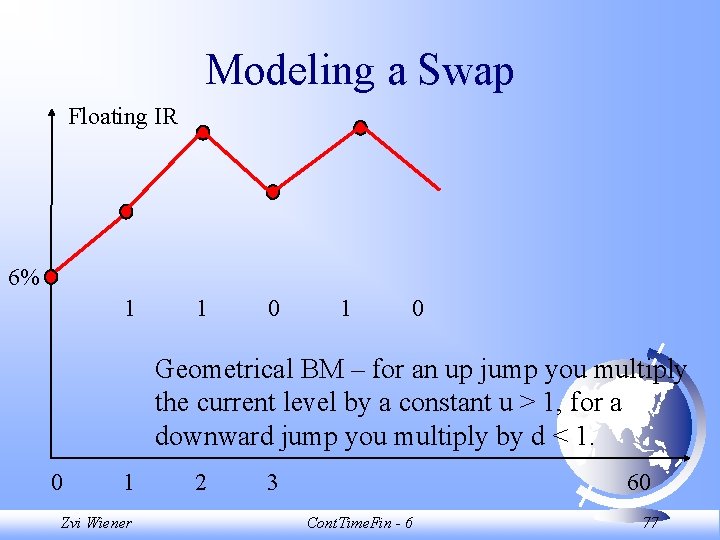
Modeling a Swap Floating IR 6% 1 1 0 Geometrical BM – for an up jump you multiply the current level by a constant u > 1, for a downward jump you multiply by d < 1. 0 1 Zvi Wiener 2 3 60 Cont. Time. Fin - 6 77

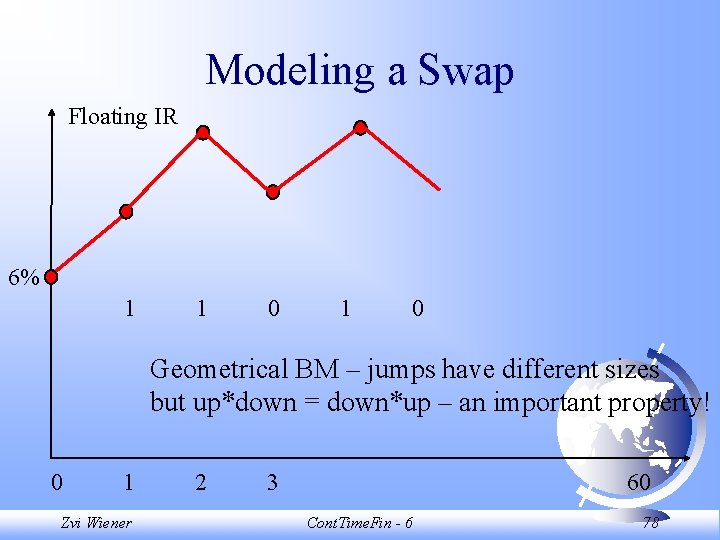
Modeling a Swap Floating IR 6% 1 1 0 Geometrical BM – jumps have different sizes but up*down = down*up – an important property! 0 1 Zvi Wiener 2 3 60 Cont. Time. Fin - 6 78

Home Assignment Evaluate the swap with your sequence of random or pseudo-random numbers using both approaches arithmetical and geometrical. Up jumps are 10 bp. , and 1. 1 Down -10 bp. , ans 0. 9 Your side is fixed, discount at 7% annually. You do not have to submit, but bring it to the class, we will discuss it. Zvi Wiener Cont. Time. Fin - 6 79

Financial Engineering New securities created: IO (negative duration) PO CMO Swaptions Caps and Caplets Floors Ratchets Zvi Wiener Cont. Time. Fin - 6 80

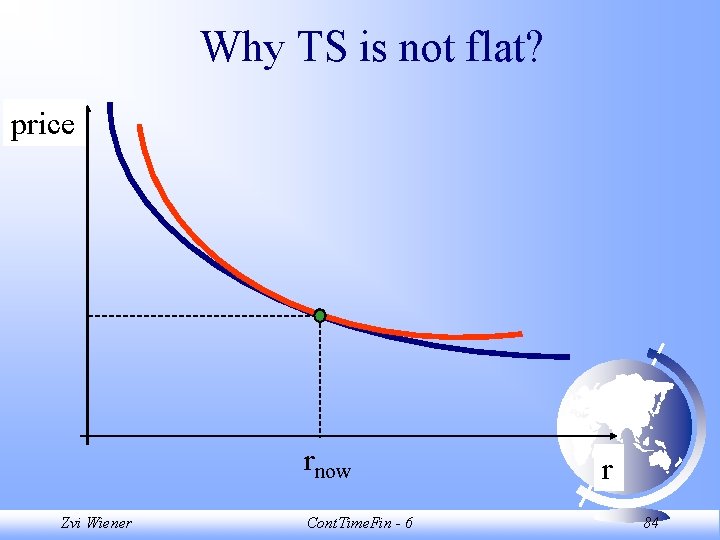
Why TS is not flat? Assume that TS is flat, but varies with time. Then the price of a zero coupon bond maturing in time is e-r. How one can form an arbitrage portfolio? Requirements: zero investment, never losses, sometimes gains. Zvi Wiener Cont. Time. Fin - 6 81

Why TS is not flat? Take 3 bonds, maturing in 1, 2, and 3 years. The current prices are: P 1 = e-r, P 2 = e-2 r, P 3 = e-3 r. We want to form a portfolio with a one-year bonds, b two-years, c three-years. So the first requirement is ae-r + be-2 r + ce-3 r=0 Zvi Wiener Cont. Time. Fin - 6 82

Why TS is not flat? So the second requirement is that there are no possible losses Equate duration of long and short sides. -ae-r - 2 be-2 r - 3 ce-3 r=0 The two equations can be solved simultaneously. Solution is a zero-investment, zero-loss portfolio - arbitrage. Zvi Wiener Cont. Time. Fin - 6 83

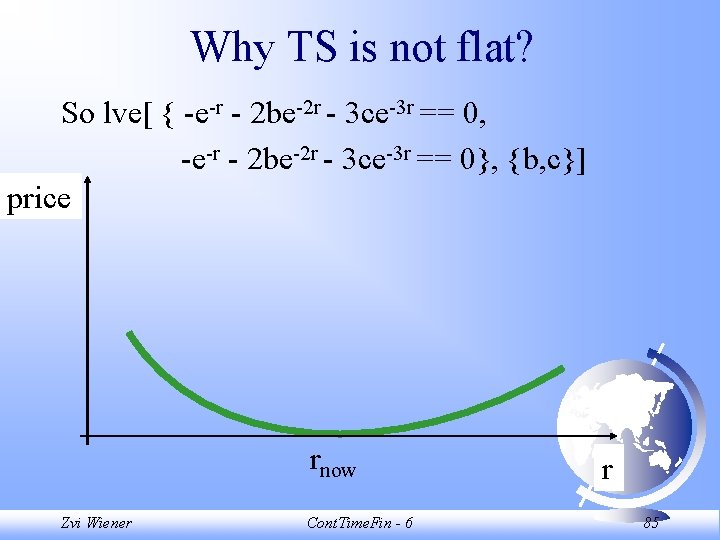
Why TS is not flat? price rnow Zvi Wiener Cont. Time. Fin - 6 r 84

Why TS is not flat? So lve[ { -e-r - 2 be-2 r - 3 ce-3 r == 0, -e-r - 2 be-2 r - 3 ce-3 r == 0}, {b, c}] price rnow Zvi Wiener Cont. Time. Fin - 6 r 85

Term Structure Models Let V(t, T) be the price at time t of an asset paying $1 at time T. Obviously V(T, T) =1. Under the equivalent martingale measure the discounted price is a martingale, so Zvi Wiener Cont. Time. Fin - 6 86

Term Structure Models Zvi Wiener Cont. Time. Fin - 6 87

One Factor Models Assume that the short rate is the only factor. Zvi Wiener Cont. Time. Fin - 6 88

One Factor Models Consider a riskless portfolio consisting of two bonds: V 1, and V 2 (with ttm T 1 and T 2). The riskless portfolio can be formed as How to choose and so that the portfolio is riskless? Zvi Wiener Cont. Time. Fin - 6 89

One Factor Models This portfolio is riskless, so it earns the risk free interest. Zvi Wiener Cont. Time. Fin - 6 90

One Factor Models Zvi Wiener Cont. Time. Fin - 6 91

One Factor Models Zvi Wiener Cont. Time. Fin - 6 92

One Factor Models Zvi Wiener Cont. Time. Fin - 6 93

One Factor Models Zvi Wiener Cont. Time. Fin - 6 94

One Factor Models Zvi Wiener Cont. Time. Fin - 6 95

One Factor Models Zvi Wiener Cont. Time. Fin - 6 96

One Factor Models Zvi Wiener Cont. Time. Fin - 6 97