Finance 30210 Managerial Economics Optimization Functions Optimization deals

Finance 30210: Managerial Economics Optimization

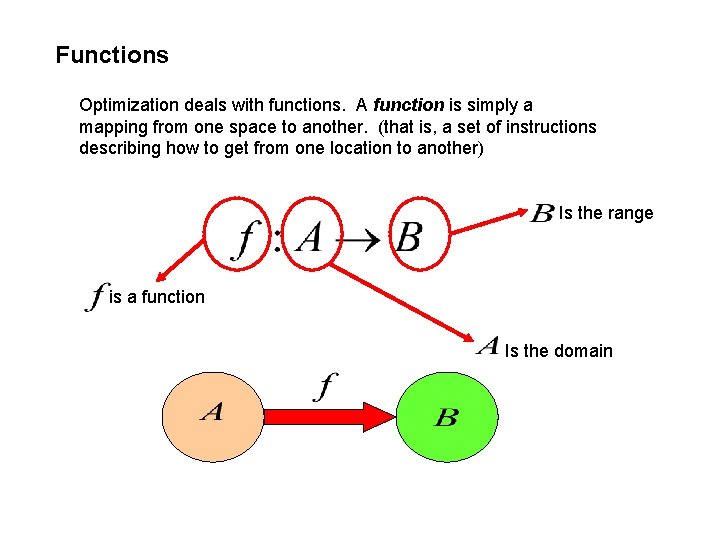
Functions Optimization deals with functions. A function is simply a mapping from one space to another. (that is, a set of instructions describing how to get from one location to another) Is the range is a function Is the domain

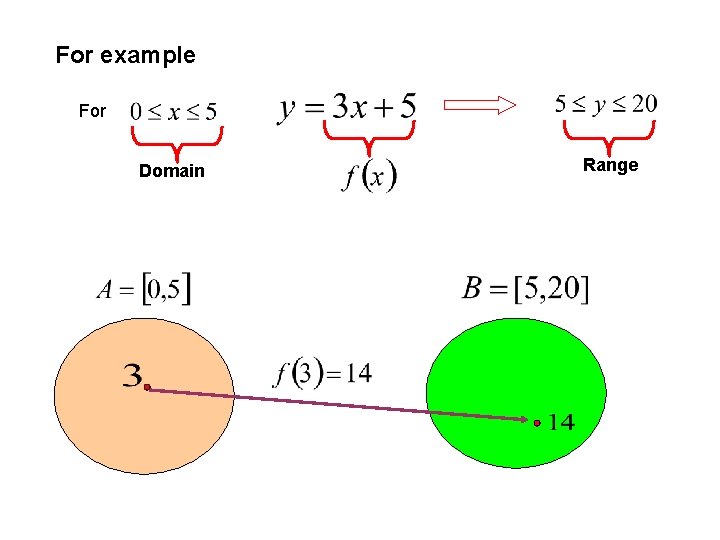
For example For Domain Range

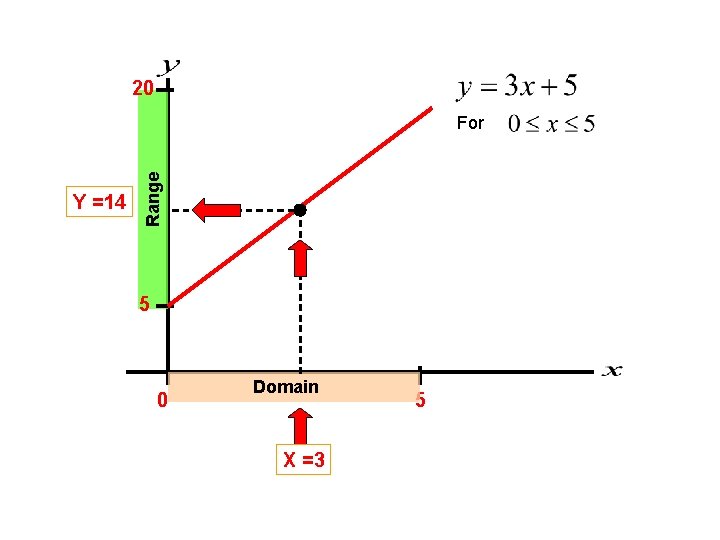
20 Y =14 Range For 5 0 Domain X =3 5

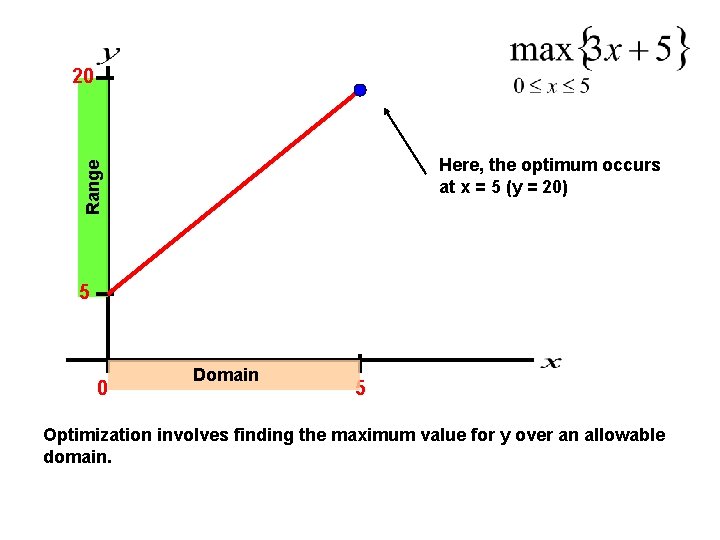
20 Range Here, the optimum occurs at x = 5 (y = 20) 5 0 Domain 5 Optimization involves finding the maximum value for y over an allowable domain.

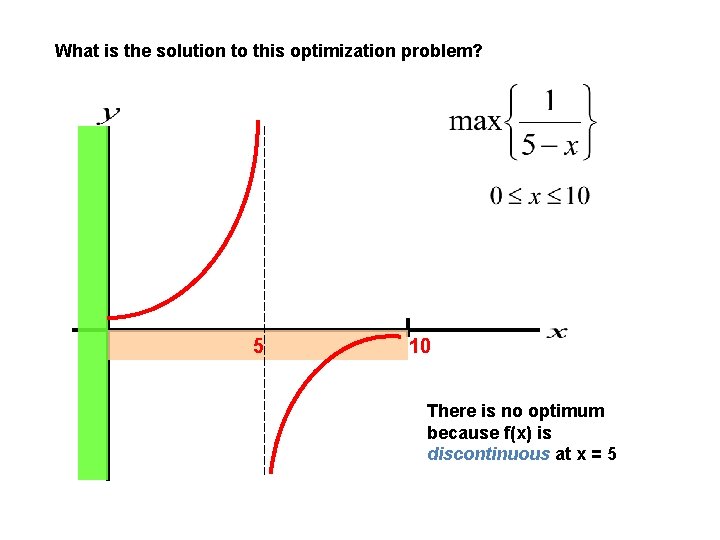
What is the solution to this optimization problem? 5 10 There is no optimum because f(x) is discontinuous at x = 5

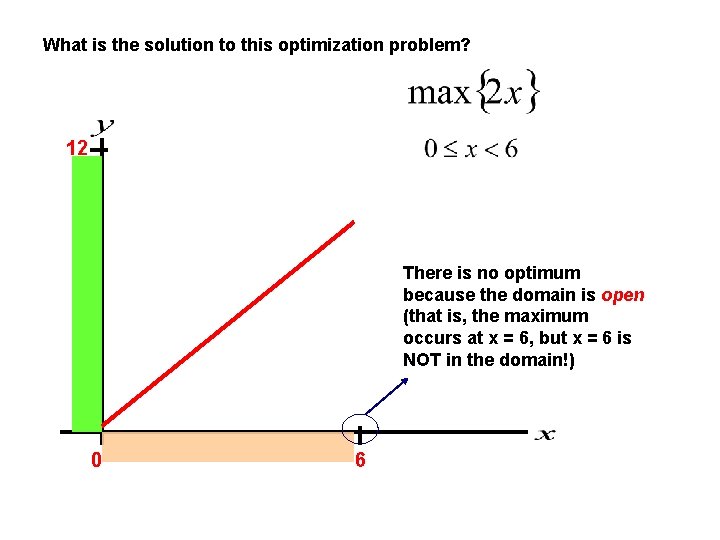
What is the solution to this optimization problem? 12 There is no optimum because the domain is open (that is, the maximum occurs at x = 6, but x = 6 is NOT in the domain!) 0 6

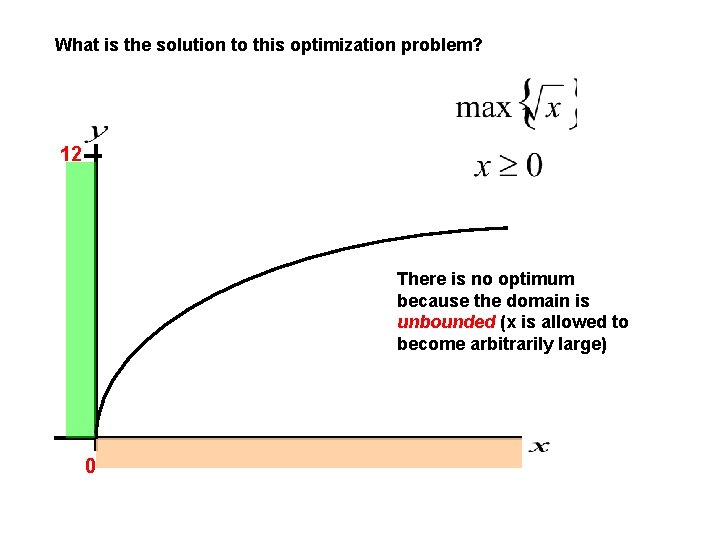
What is the solution to this optimization problem? 12 There is no optimum because the domain is unbounded (x is allowed to become arbitrarily large) 0

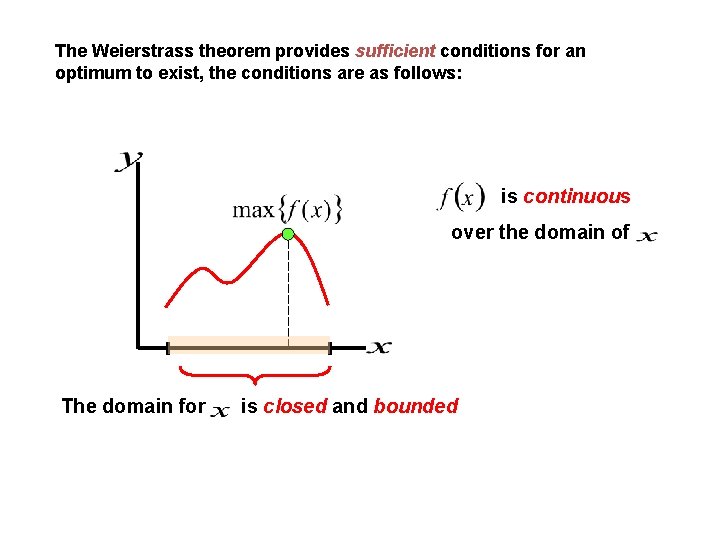
The Weierstrass theorem provides sufficient conditions for an optimum to exist, the conditions are as follows: is continuous over the domain of The domain for is closed and bounded

Derivatives Formally, the derivative of is defined as follows: All you need to remember is the derivative represents a slope (a rate of change) Actually, to be more accurate, the derivative represents a trajectory

Useful derivatives Linear Functions Exponents Logarithms Products Composites

Practice Makes Perfect…

Unconstrained maximization Strictly speaking, no problem is truly unconstrained. However, sometimes the constraints don’t “bite” (the constraints don’t influence the maximum) First Order Necessary Conditions If is a solution to the optimization problem or then

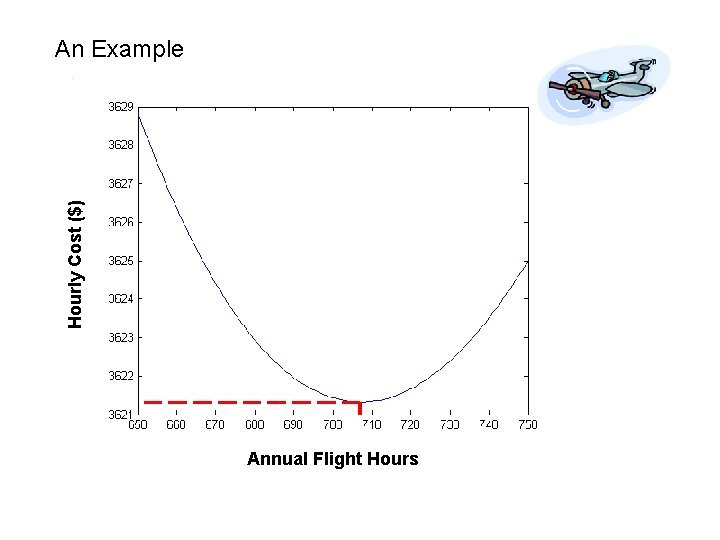
An Example Suppose that your company owns a corporate jet. Your annual expenses are as follows: ØYou pay your flight crew (pilot, co-pilot, and navigator a combined annual salary of $500, 000. ØAnnual insurance costs on the jet are $250, 000 ØFuel/Supplies cost $1, 500 per flight hour ØPer hour maintenance costs on the jet are proportional to the number of hours flown per year. Maintenance costs (per flight hour) = 1. 5(Annual Flight Hours) If you would like to minimize the hourly cost of your jet, how many hours should you use it per year?

An Example Let x = Number of Flight Hours First Order Necessary Conditions

Hourly Cost ($) An Example Annual Flight Hours

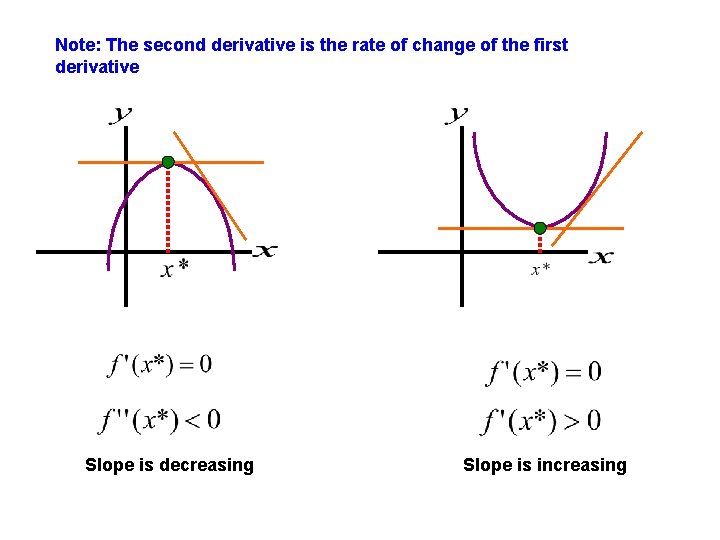
How can we be sure we are at a minimum? Secondary Order Necessary Conditions If is a solution to the maximization problem then If is a solution to the minimization problem then

Note: The second derivative is the rate of change of the first derivative Slope is decreasing Slope is increasing

An Example Let x = Number of Flight Hours First Order Necessary Conditions Second Order Necessary Conditions For X>0

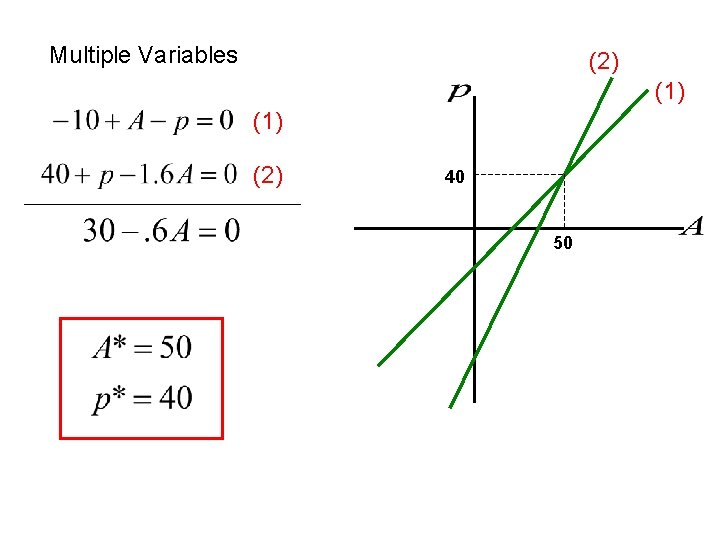
Multiple Variables Suppose you know that demand for your product depends on the price that you set and the level of advertising expenditures. Choose the level of advertising AND price to maximize sales

Partial Derivatives When you have functions of multiple variables, a partial derivative is the derivative with respect to one variable, holding everything else constant First Order Necessary Conditions

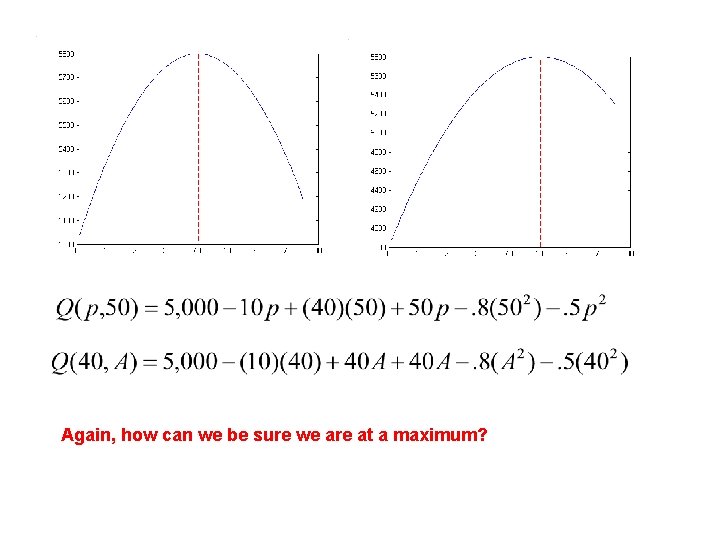
Multiple Variables (2) (1) (2) 40 50

Again, how can we be sure we are at a maximum?

Recall, the second order condition requires that its generally sufficient to see if all the second derivatives are negative…

Practice Questions 1) Suppose that profits are a function of quantity produced and can be written as Find the quantity that maximizes profits 2) Suppose that costs are a function of two inputs and can be written as Find the quantities of the two inputs to minimize costs

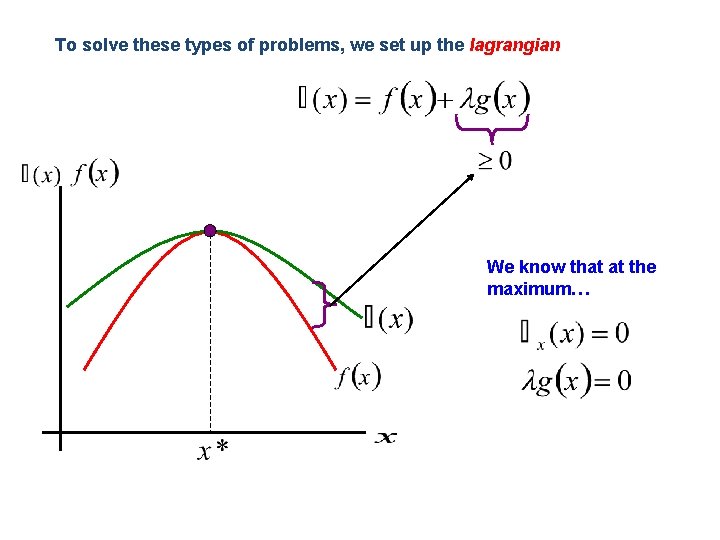
Constrained optimizations attempt to maximize/minimize a function subject to a series of restrictions on the allowable domain To solve these types of problems, we set up the lagrangian Function to be maximized Constraint(s) Multiplier

To solve these types of problems, we set up the lagrangian We know that at the maximum…

Once you have set up the lagrangian, take the derivatives and set them equal to zero First Order Necessary Conditions Now, we have the “Multiplier” conditions…

Constrained Optimization Example: Suppose you sell two products ( X and Y ). Your profits as a function of sales of X and Y are as follows: Your production capacity is equal to 100 total units. Choose X and Y to maximize profits subject to your capacity constraints.

Constrained Optimization Multiplier The first step is to create a Lagrangian Objective Function Constraint

Constrained Optimization First Order Necessary Conditions “Multiplier” conditions

Constrained Optimization:

The Multiplier Lambda indicates the marginal value of relaxing the constraint. In this case, suppose that our capacity increased to 101 units of total production. Assuming we respond optimally, our profits increase by $5

Another Example Suppose that you are able to produce output using capital (k) and labor (l) according to the following process: The prices of capital and labor are and respectively. Union agreements obligate you to use at least one unit of labor. Assuming you need to produce units of output, how would you choose capital and labor to minimize costs?

Minimizations need a minor adjustment… To solve these types of problems, we set up the lagrangian A negative sign instead of a positive sign!!

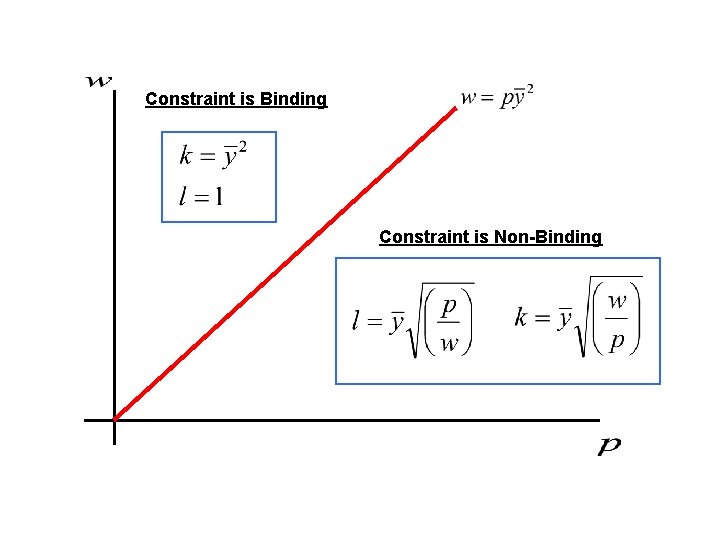
Non-Binding Constraints Just as in the previous problem, we set up the lagrangian. This time we have two constraints. Will hold with equality Doesn’t necessarily hold with equality

First Order Necessary Conditions

Case #1: First Order Necessary Conditions Constraint is non-binding

Case #2: First Order Necessary Conditions Constraint is binding

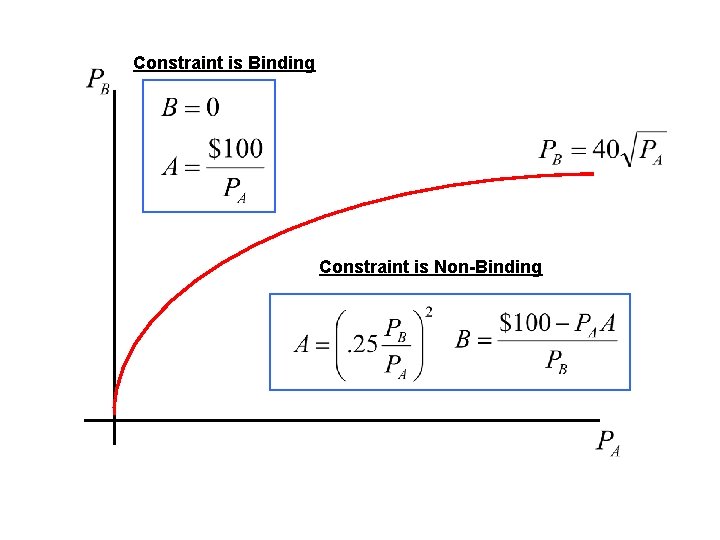
Constraint is Binding Constraint is Non-Binding

Try this one… You have the choice between buying apples and bananas. You utility (enjoyment) from eating apples and bananas can be written as: The prices of Apples and Bananas are given by and Maximize your utility assuming that you have $100 available to spend

(Objective) (Income Constraint) (You can’t eat negative apples/bananas!!) Objective Income Constraint Non-Negative Consumption Constraint

First Order Necessary Conditions We can eliminate some of the multiplier conditions with a little reasoning… 1. You will always spend all your income 2. You will always consume a positive amount of apples

Case #1: Constraint is non-binding First Order Necessary Conditions

Case #1: Constraint is binding First Order Necessary Conditions

Constraint is Binding Constraint is Non-Binding