Final Presentation 3 D Mechanical Object Reconstruction Muharrem

Final Presentation 3 D Mechanical Object Reconstruction Muharrem Mercimek 12. 06. 2005 1

Contents Task 1: ECE 572: Digital Image Processing Task 2: ECE 573: Implementation 3 D Reconstruction Task 3: ECE 672: Survey: 3 D Registration Task 4: Instrumentation: Data acquisition 2

Contents TASK 1 ECE 573 IMPLEMENTATION: 3 D RECONSTRUCTION 1. Introduction Applications Motivation 2. 3 D Reconstruction Blocks Data Acquisition 3 D Registration Data integration 3. Implementation using Rapidform 04 and Gaussian Fields Framework 4. Experimental Results 3

Introduction Applications: • Architectural or Industrial Plans into 3 D Computer Aided Design (CAD) models. • Comparison of CAD models with instance of part to determine errors in manufacturing process. • Design verification of buildings. • Object modeling for surveillance, inspection, navigation, and automatic recognition tasks. • Object recognition - alignment of object model instance and image of unknown object. My motives: 3 D reconstruction and modeling of small mechanical objects from multiple views acquired using range scanners. 4
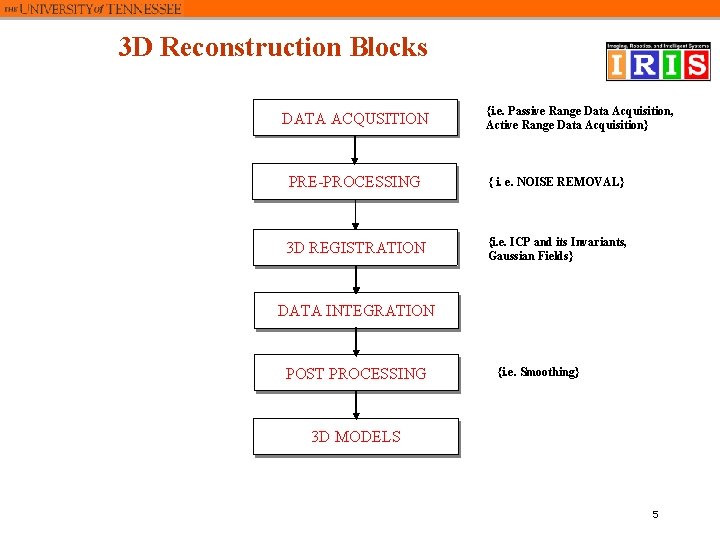
3 D Reconstruction Blocks DATA ACQUSITION {i. e. Passive Range Data Acquisition, Active Range Data Acquisition} PRE-PROCESSING { i. e. NOISE REMOVAL} 3 D REGISTRATION {i. e. ICP and its Invariants, Gaussian Fields} DATA INTEGRATION POST PROCESSING {i. e. Smoothing} 3 D MODELS 5

Data Acquisition Passive Data Acquisition; 1. Stereo Vision; Stereo-vision systems use the same principles of parallax and triangulation employed by human vision to reconstruct the geometry of objects. 2. • • Constraints are; The matching or correspondence task. The rapid decrease in depth accuracy with the increase in the distance. Active Data acquisition: Range Scanners; 1. Continuous wave modulation approach: 2. Time of flight approach: 3. Laser triangulation approach: 4. Structured light triangulation approach: 6

Data Acquisition Range Scanners; Time of flight approach: Based on time off flight send out the laser beam and detect the reflection. By measuring the travel time, the distance between the scanner and the object where the laser hits can be calculated. (Riegl LMS Z 210) Riegl 3 d Terrestrial Laser scanner www. riegl. com Resolution 5 mm Min range 4 m Max range 400 m Field of view 80 deg vertical 360 deg horizontal Measurement Rate 12 000 points/sec 7
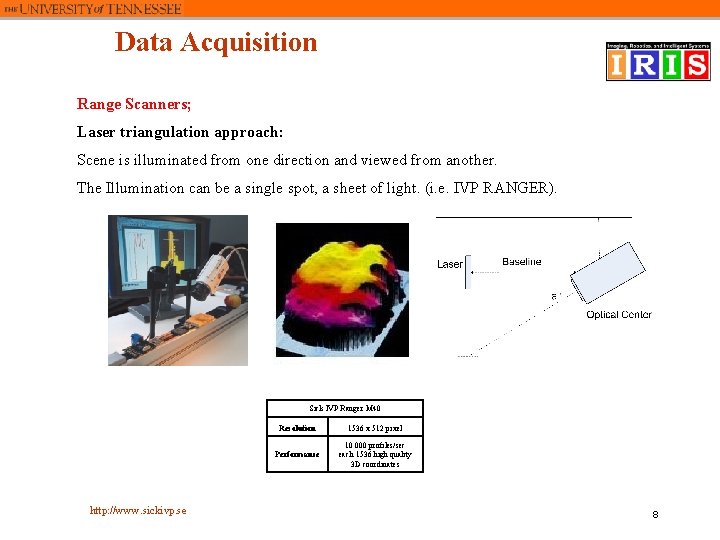
Data Acquisition Range Scanners; Laser triangulation approach: Scene is illuminated from one direction and viewed from another. The Illumination can be a single spot, a sheet of light. (i. e. IVP RANGER). Sick IVP Ranger M 40 http: //www. sickivp. se Resolution 1536 x 512 pixel Performance 10 000 profiles/sec each 1536 high quality 3 D coordinates 8

Data Acquisition Range Scanners; Structured light triangulation approach: Based on the same theory used in laser triangulation approach except the illumination here is a structured or coded light projection (Genex 3 D Face. Cam) Genex 3 D Face. Cam www. genextech. com 3 D Resolution 640 x 480 points Field of view 510 mm Width 400 mm Height 300 mm Depth Scene Acquisition Time Processing Time 400 msec 1 -30 sec 9

Data Acquisition Possible Problems during Data Acquisition are; Calibration problem: Camera calibration essentially involves transforming the range image data into camera coordinates x, y, and z. Lighting problem: The changes in the lighting during data acquisition cause confusions about the real texture of the object Occlusion problem: The occlusion problem results from surfaces on a part occluding or obstructing the view of other surfaces on the same part Mobility problem: Mobility is sometimes paramount to 3 D scene reconstruction. All scene geometry needs to be adequately represented and sufficient visual details must be acquired for surface rendering through mobile sensors. 10

Data Acquisition 1 -Viewer-centered: • Viewer-centered coordinate systems are easy to construct • Surface description changes with the viewpoint. • Surfaces have to be aligned before comparison. • Separate representations must be stored for each viewpoint. 2 -Object-centered: • Object is described in a coordinate system fixed to the object. • The description of the surface is view independent, so surfaces can be directly compared, without aligning the surfaces. • Finding a coordinate system is tough. 11

3 D Registration 3 D registration, is the problem of matching two or more overlapping scans to build a consistent model, thus extrapolating the relative pose of one set with respect to the other. Steps for a General Image Registration Process − Analyze the images. − Determine the appropriate corresponding image primitives. − Determine the transformation model. {Similarity, Affine, Projective, Non-linear, Deformable} − Develop constraints and an error metric on the transformation estimate. {Sum of Square Error} − Design a minimization algorithm. {Gradient / Steepest Descent, Newton’s method} − Develop a convergence criteria. How to find correspondences, How to find Transformation Function, How to find Transformation parameters, 12

3 D Registration ICP: • Align two partially-overlapping images given initial guess for relative transform. • If correct correspondences are known, it is possible to find correct relative rotation/translation. • How to find corresponding points is a problem. • Previous systems based on user input, feature matching, surface signatures, etc. • Alternative: Assume closest points correspond to each other, compute the best transform. And iterate to find alignment. Besl, P. J. and Mc. Kay, N. D. ‘A method for registration of 3 D shapes’, IEEE Trans. Patt. Anal. Machine Intell. , Vol. 14, No. 2, pp. 239 -256, (1992) 13

3 D Registration ICP: The algorithm of the ICP can be explained as follows, 1. Start with an initial transformation 2. For for or until stopping criteria met do 2. 1 Compute 2. 2 Build the correspondence set 2. 3 Using the pairs C compute the transformation that minimizes the sum of the square errors. • At each iteration, it first creates closest point correspondences between two sets of points (or more generally geometric data). • Then minimizes the average distance of the previously found correspondences by a rigid transformation - a translation and a rotation. 14

3 D Registration ICP: ICP is has some shortcomings; • It is a point-based method that does not consider the local shape of the surface around each point; • The frequent nearest neighbor searches have quadratic complexity and are computationally expensive. • ICP methods indeed need starting points rather close to the global rigid motion parameters in order not to got trapped by local minima, • Requires large overlap between the datasets to be aligned. 15

3 D Registration Gaussian Fields Framework • A new energy function that quantifies the registration. • The strength of the Gaussian force field depend on the distance between the points and on the similarity of their shape. • In addition to creating an energy function, a robust feature descriptor for general unorganized and noisy point-sets can be devised through tensor voting feature extractor. • A significant increase in the range of convergence as compared with ICP. F. Boughorbel, “Multimodal Three Dimensional Scene Reconstruction, The Gaussian Fields Framework”, Ph. D thesis, The University of Tennessee, Knoxville, 2005. 16

3 D Registration Gaussian Fields Framework Data sets: Gaussian Field: Criterion: 17

Data Integration By “integration, ” it is generally referred to the merging of independent (but registered) meshes to form a single polygonal mesh without defects such as dangling edges or topology violations. To optimize the mesh representation for a specific application or use. This often results in a coarsening of the mesh (i. e. , reduction of the vertex and polygon count) in response to application demands or other constraints. 18

Experiments Data Acquisition System, Objects. 19
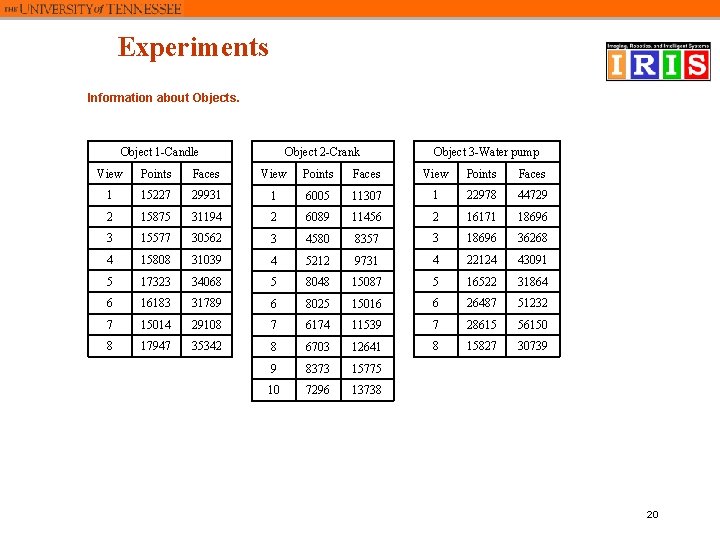
Experiments Information about Objects. Object 2 -Crank Object 1 -Candle Object 3 -Water pump View Points Faces 1 15227 29931 1 6005 11307 1 22978 44729 2 15875 31194 2 6089 11456 2 16171 18696 3 15577 30562 3 4580 8357 3 18696 36268 4 15808 31039 4 5212 9731 4 22124 43091 5 17323 34068 5 8048 15087 5 16522 31864 6 16183 31789 6 8025 15016 6 26487 51232 7 15014 29108 7 6174 11539 7 28615 56150 8 17947 35342 8 6703 12641 8 15827 30739 9 8373 15775 10 7296 13738 20

Experimental Results Object 1 8 views (textured) Textured Rapid. Form 04 model 21

Experimental Results Object 1 8 views (textured) Gaussian Fields model 22

Experimental Results Object 2 10 views (textured) Textured Rapid. Form 04 model 23
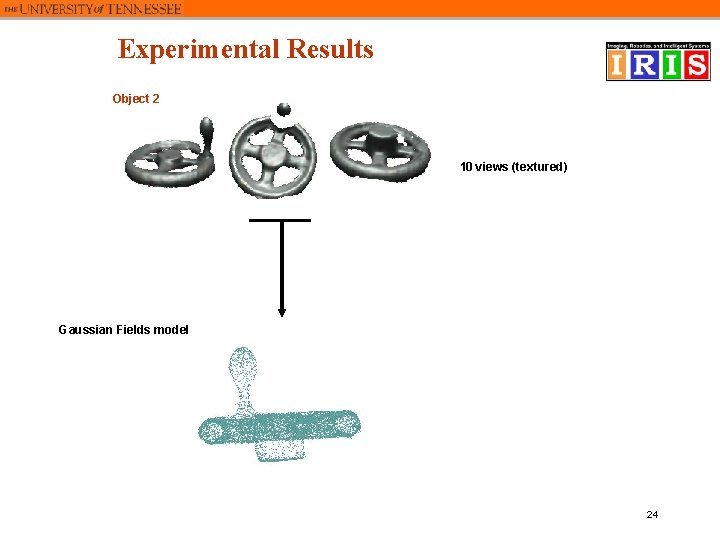
Experimental Results Object 2 10 views (textured) Gaussian Fields model 24

Experimental Results Object 3 8 views (textured) Textured Rapid. Form 04 model 25

Experimental Results Object 3 8 views (textured) Gaussian Fields model 26

Contents TASK 2 ECE 672 SURVEY: 3 D REGISTERATION 1. Icp and its variants 2. Point and surface normals based 3 D registration 3. Special Feature based 3 D registration 27

ICP and Its Variants P. J. Besl, and N. D Mc. Kay. , “A method for registration of 3 D shapes”, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 14, No. 2, pp. 239 -256, (1992). – Was an alternative method to solve corresponding points problem. – Repeatedly updates the relative pose by minimizing the sum of squared distances between closest points on the two surfaces (point-to-point matching). Y. Chen, and G. Medioni, “Object modeling by registration of multiple range images”, Image and Vision Computing, 10 (3), 145– 155, 1992. – A similar method in which the distance between points and tangent planes is minimized (point-to-plane matching). Z. Zhang, “Iterative point matching for registration of free-form curves and surfaces”, International Journal of Computer Vision, 13(2): 119– 152, 1994. – The first improvement used k-dimensional trees to speed up the closest point search computation. – The second improvement uses robust statistics to generate a dynamic distance threshold on the distance allowed between closest points. 28

ICP and Its Variants A. Johnson and S. B. Kang, Registration and integration of textured 3 -D data, Image Vision Comput. 17, 1999, 135 -147. – Color Icp: Shape and color information to improve the registration beyond that obtained with an ICP algorithm. S. Rusinkiewicz and M. Levoy, “Efficient variants of the ICP algorithm”, In Proceedings of the Third International Conference on 3 D Digital Imaging and Modeling, pp. 145– 152, Quebec City, Canada, May 2001. – Many variants of ICP have been proposed affecting all the phases of the algorithm: 1. 2. 3. 4. 5. 6. Selection of some set of points in one or both meshes. Matching these points to samples in the other mesh. Weighting the corresponding pairs appropriately. Rejecting certain pairs based on looking at each pair individually or considering the entire set of pairs. Assigning an error metric based on the point pairs. Minimizing the error metric. 29

Point and surface normals based 3 D registration P. Biber and W. Straßer, “The normal distributions transform: A new approach to laser scan matching”, In IEEE/RJS International Conference on Intelligent Robots and Systems, Las Vegas, October 2003. M. Magnusson, and T Duckett, “A Comparison of 3 D Registration Algorithms for Autonomous Underground Mining Vehicles” Proc. 2 nd European Conference on Mobile Robots (ECMR), Ancona, Italy, September 7 -10, 2005. – Normal distributions transform: Addresses two main problems of ICP, the fact that it does not make any use of local surface shape, and the computationally demanding nearest-neighbor search. – Instead of matching the source point cloud to the points in the target directly, the probability of measuring a point at a certain position is modeled by a linear combination of normal distributions. 30

Point and surface normals based 3 D registration E. Johnson and M. Hebert. , “Using Spin-Images for Efficient Multiple Model Recognition in Cluttered 3 -D Scenes” IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(5): 433– 449, 1999. – Spin-images are descriptive images that encodes global properties of the surfaces. – A new representation using 3 D vertex coordinates p and the surface normal n at the vertex. – Matching algorithm using spin images are; • • • Compare the spin images from points on two surfaces, Establish point correlation, Store all spin images from the model in a stack, Compare the spin image of a vertex on the scene to a best-match Make Point correlation between these two points. Group point correspondences, eliminate outliers. 31

Point and surface normals based 3 D registration N. Brusco, M. Andreetto, and G. M Cortelazzo, “ 3 D Registration by Textured Spin Images”, The 5 th International Conference on 3 -D Digital Imaging and Modeling (3 DIM 05), pp. 262269, Banff, Alberta, Canada June 13 -16, 2005. Textured spin images: Extension of Spin images matching method through including textural information. – Textured spin-images are more robust than spin-mages, – Estimates rigid motion’s parameters more precise than those obtained by spin-images. S. Okatani, and K. Deguchi, “A Method for Fine Registration of Multiple View Range Images Considering the Measurement Error Properties”, Computer Vision and Image Understanding, 87, 66– 77 , 2002. − The most probable transformation of the second image to overlay it onto the first image considering the measurement error distributions was estimated. − One of the range images was represented as a set of triangular patches and the other as a set of points. − For a given transformation, the positions of every measured point both in the two range images were corrected according to the individual variance of its measurement error. 32

Special Feature based 3 D registration Feature: – The main problem with search structures is that they lose a lot of their speeding up advantages when datasets are large and far from each other. – Using less point matching or reducing the set of surface points are needed for an efficient registration. – Feature extraction is the process of locating an outstanding part, quality, or characteristics in a given scene. J. -P. Thirion, “New feature points based on geometric invariants for 3 D image registration”, Int. J. of Computer Vision, 18(2), pp. 121 -137, 1996 – 3 D partial description, surface patches. – In order to quickly match 3 D patches detecting special points or curves on them. – Invariant descriptions of the landmarks ease the matching even further. 33

Special Feature based 3 D registration J. Vanden Wyngaerd, L. Van Gool, R. Koch, and M. Proesmans, “Invariant-based registration of surface patches, ” in Proc. Int. Conf. Computer Vision (ICCV'99), pp. 301 -306, 1999 Bitangent curve matching: – Extraction and invariant characterization of bitangent curve pairs. – Bitangent curves are good landmarks as they are invariant under Euclidean, affine, and even under projective transformations and are sufficiently numerous. K. Higuchi, M. Hebert and Ikeuchi K. “Building 3 -D models from unregistered range images”, Graphical Models and Image Processing, 57(4), pp: 315 -333 July 1995. Spherical Attribute Image Matching: – Invariant features to Euclidean transform can be used. – A Gaussian curvature calculation at each node of the mesh – Mapping the meshes on a unit sphere, – Matching of viewpoints by comparing the unit sphere. 34

Special Feature based 3 D registration A. P. Ashbrook, R. B. Fisher, C. Robertson and N. Werghi, "Aligning Arbitrary Surfaces using Pairwise Geometric Histograms", Proc. NOBLESSE Workshop on Non-linear Model Based Image Analysis NMBIA 98, Glasgow, Scotland, pp 103 --108, 1 -3 July 1998. Geometric Histogram Matching: – A pairwise geometric histogram is constructed for each triangular facet in a given mesh which describes its pairwise relationship with each of the other surrounding facets within a predefined distance. – This distance controls the degree to which the representation is a local description of shape. The histogram encodes the surrounding shape geometry in a manner which is invariant to rigid transformations of the surface data. – A disadvantage of this algorithm is input surfaces should be smooth enough for a good feature extraction. 35

Special Feature based 3 D registration S. M. Yamany, A. A. Farag, “Free-form surface registration using surface signatures”, In: Int. Conf. on Computer Vision, Vol. 2, 1999, pp. 1098– 1104. The surface signature Matching: – Captures the surface curvature information, seen from certain points and produces images, at these points. – This 2 D image represents a signature of the 3 D surface at that point due to the fact that it is almost unique for each point location on the surface. – Surface registration is then performed by matching signature images of different surfaces and hence finding corresponding points in each surface. – Surface signature matching can be criticized as depending on high curvature, smooth surface lacks of correctly matching. 36
Special Feature based 3 D registration A. P. Ashbrook, R. B. Fisher, C. Robertson and N. Werghi, "Aligning Arbitrary Surfaces using Pairwise Geometric Histograms", Proc. NOBLESSE Workshop on Non-linear Model Based Image Analysis NMBIA 98, Glasgow, Scotland, pp 103 --108, 1 -3 July 1998. Harmonic shape image matching: – 2 D representations of the 3 D surfaces. – Given a 3 D surface patch with disc topology and a selected 2 D planar domain, a harmonic map is constructed by a two-step process which includes boundary mapping and interior mapping. – They are unique, preserve both the shape and the continuity of the underlying surfaces. – They provide a general framework to represent surface attributes such as surface normal, color, texture and material. – Harmonic Shape Images are discriminative and stable, and they are robust with respect to surface sampling resolution and occlusion. 37

Special Feature based 3 D registration 1. C. Chua, and R. Jarvis, “Point signatures: a new representations for 3 D object recognition”, Int. J. Comput. Vision, 25 (1), 63– 85, 1997. 2. Point signature matching: – Point signatures is a surface representation for free-form surfaces. – This representation is able to describe a 3 D data point more completely by including the structural information around that point. – Distance and angular features are extracted from each region, and are represented using 2 D signatures. – Surface signature matching is application specific in the sense that it selects interest-points of high curvature around which to construct localized regions. – This makes input surfaces with fewer topological features more difficult to match. 38

Conclusion and Future works − An experimental study using two effective tools to show what is the final output of a 3 D modeling process. − Overlapping range images are used for a multi-view registration. − Rapid. Form. TM 2004 software which uses a registration approach on ICP and a new tool Gaussian Fields framework is used to experiment on range data. − Survey study addresses the basics of 3 D registration and the most efficient algorithms that have been studied recently. − Own registration algorithm using c++. − Data acquisition using other Riegl and sick scanners. 39

40
- Slides: 40