Final Physics 101 Lecture 20 Waves Physics 101










- Slides: 14

Final Physics 101: Lecture 20 Waves Physics 101: Lecture 20, Pg 1

Types of Waves l Transverse: The medium oscillates perpendicular to the direction the wave is moving. èWater (more or less) èThe “Wave” l Longitudinal: The medium oscillates in the same direction as the wave is moving èSound Physics 101: Lecture 20, Pg 2 8

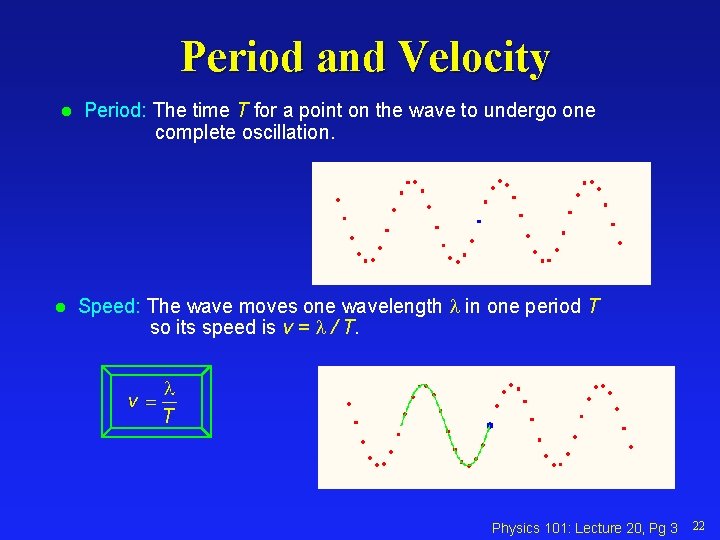
Period and Velocity l l Period: The time T for a point on the wave to undergo one complete oscillation. Speed: The wave moves one wavelength in one period T so its speed is v = / T. Physics 101: Lecture 20, Pg 3 22

Slinky Question Suppose that a longitudinal wave moves along a Slinky at a speed of 5 m/s. Does one coil of the slinky move through a distance of five meters in one second? 1. Yes 2. No 5 m Physics 101: Lecture 20, Pg 4 12

Harmonic Waves Wavelength: The distance between identical points on the wave. Amplitude: The maximum displacement A of a point on the wave. Angular Frequency w: w = 2 p f Wave Number k: k = 2 p / Recall: f = v / y Wavelength Amplitude A A x Physics 101: Lecture 20, Pg 5 20

Example: microwave l The wavelength of microwaves generated by a microwave oven is about 3 cm. At what frequency do these waves cause the water molecules in your burrito to vibrate ? The speed of light is c = 3 x 108 m/s Physics 101: Lecture 20, Pg 6 29

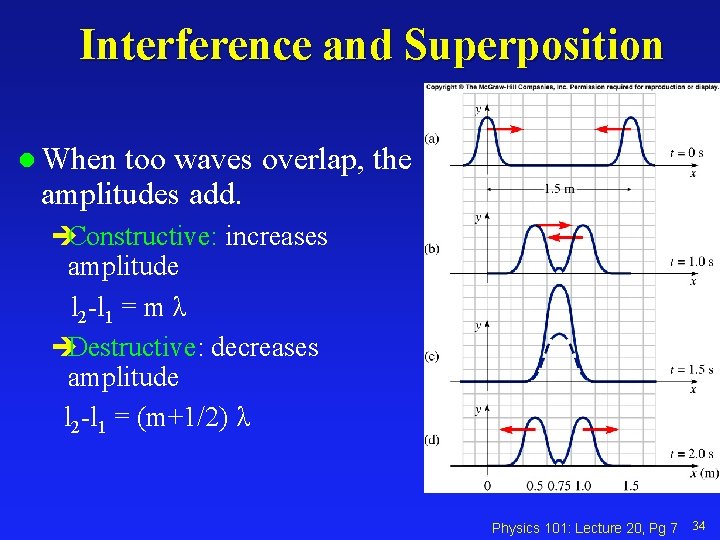
Interference and Superposition l When too waves overlap, the amplitudes add. èConstructive: increases amplitude l 2 -l 1 = m λ èDestructive: decreases amplitude l 2 -l 1 = (m+1/2) λ Physics 101: Lecture 20, Pg 7 34

Example: two speakers l Two speakers are separated by a distance of 5 m and are producing a monotone sound with a wavelength of 3 m. Other than in the middle, where can you stand between the speakers and hear constructive interference? Physics 101: Lecture 20, Pg 8

Example: two speakers l Two speakers are separated by a distance of 5 m and are producing a monotone sound with a wavelength of 3 m. Where can you stand between the speakers and hear destructive interference? Physics 101: Lecture 20, Pg 9

Reflection Act l. A slinky is connected to a wall at one end. A pulse travels to the right, hits the wall and is reflected back to the left. The reflected wave is A) Inverted B) Upright èFixed boundary reflected wave inverted èFree boundary reflected wave upright Physics 101: Lecture 20, Pg 10 37

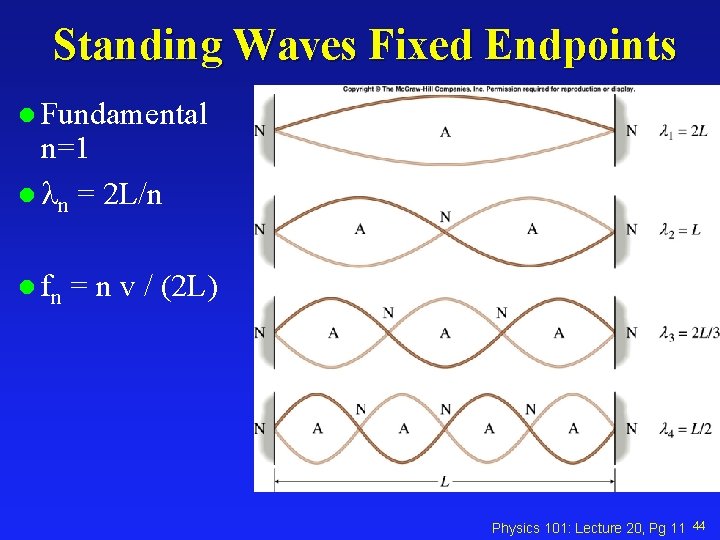
Standing Waves Fixed Endpoints l Fundamental n=1 l n = 2 L/n l fn = n v / (2 L) Physics 101: Lecture 20, Pg 11 44

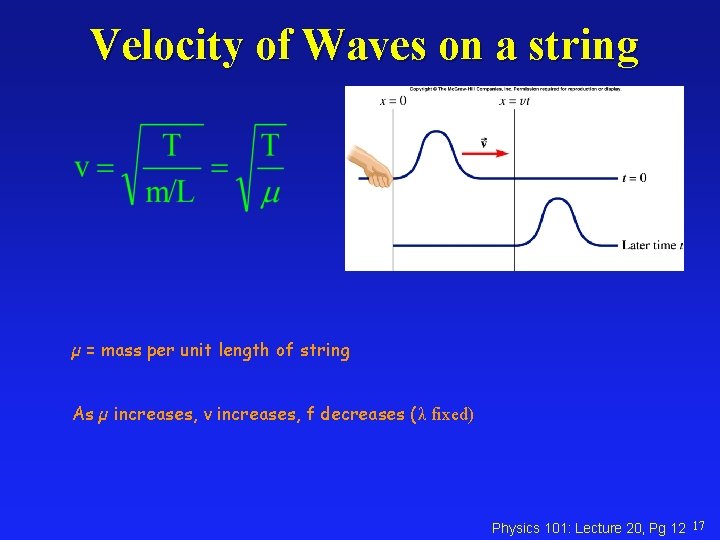
Velocity of Waves on a string µ = mass per unit length of string As µ increases, v increases, f decreases (λ fixed) Physics 101: Lecture 20, Pg 12 17

Example: guitar A guitar’s E-string has a length of 65 cm and is stretched to a tension of 82 N. If it vibrates with a fundamental frequency of 329. 63 Hz, what is the mass of the string? Physics 101: Lecture 20, Pg 13 48

Summary l Wave Types èTransverse (eg pulse on string, water) èLongitudinal (sound, slinky) l Harmonic èy(x, t) = A cos(wt –kx) or A sin(wt – kx) l Superposition èJust add amplitudes l Reflection (fixed point inverts wave) l Standing Waves (fixed ends) è n = 2 L/n èfn = n v / 2 L Physics 101: Lecture 20, Pg 14 50
 Physics 101 lecture notes pdf
Physics 101 lecture notes pdf Physics 101 lecture 1
Physics 101 lecture 1 Physics 101 lecture notes pdf
Physics 101 lecture notes pdf Wave notes pdf
Wave notes pdf Physics 101 final exam
Physics 101 final exam 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Difference between mechanical and electromagnetic waves
Difference between mechanical and electromagnetic waves Longitudinal wave vs transverse wave
Longitudinal wave vs transverse wave Examples of mechanical wave
Examples of mechanical wave Similarities of mechanical waves and electromagnetic waves
Similarities of mechanical waves and electromagnetic waves Characteristics of a longitudinal wave
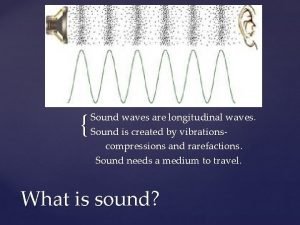
Characteristics of a longitudinal wave Sound waves longitudinal waves
Sound waves longitudinal waves Carbon dioxide temperature
Carbon dioxide temperature Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Electromagnetic waves vs mechanical waves
Electromagnetic waves vs mechanical waves