FIMAAS UTP Fsica I Sesin N 1 Vector

FIMAAS UTP Física I. Sesión Nº 1: ØVector unitario. ØÁngulos y cosenos directores. ØOperaciones vectoriales con vectores unitarios: Adición, sustracción. ØProductos vectoriales: producto escalar, producto vectorial, triple producto escalar, triple producto vectorial.

VECTORES CAPÍTULO 2 FÍSICA I FACULTAD DE CIENCIAS UNI ARTURO TALLEDO (DOCTOR EN FÍSICA)

VECTORES. • 1) Cantidades escalares, vectoriales y tensoriales. • 2) Operaciones con vectores. • • • 2. 1) Suma y resta. 2. 2) Producto por un escalar. 2. 3) Producto escalar de dos vectores. 2. 4) Producto vectorial de dos vectores. 3) Otros conceptos importantes relativos a vectores. 3. 1) Vector Unitario. 3. 2) Componentes de un vector. 4) Componentes cartesianas de un vector. Operaciones de vectores usando componentes cartesianas.

Cantidades escalares, vectoriales y tensoriales. • En Física necesitamos definir diferentes tipos de conceptos, siendo tal vez los más importantes, aquellos susceptibles de medida como posición, tiempo, fuerza, velocidad, masa, permitividad eléctrica, etc. • Las cantidades escalares son aquellas quedan bien definidas por un número real. • Las cantidades vectoriales necesitan que se especifique dirección y sentido. • Las cantidades tensoriales se refieren a propiedades de los cuerpos que varían al cambiar la dirección.

Definición de vector. Así como los números reales son entes abstractos sobre los cuales se definen varias operaciones y en Física son usados para describir a las magnitudes escalares, los vectores también son entes abstractos que los usaremos en Física para describir Las magnitudes vectoriales tales como desplazamiento, velocidad, fuerza, etc.

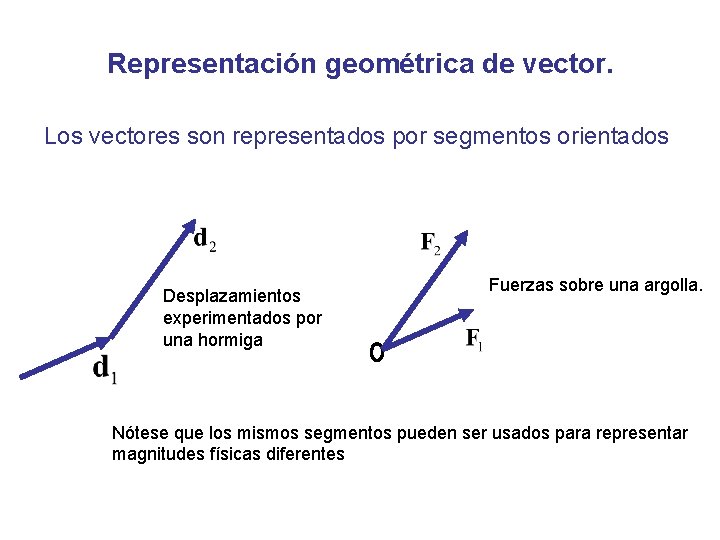
Representación geométrica de vector. Los vectores son representados por segmentos orientados Desplazamientos experimentados por una hormiga Fuerzas sobre una argolla. Nótese que los mismos segmentos pueden ser usados para representar magnitudes físicas diferentes

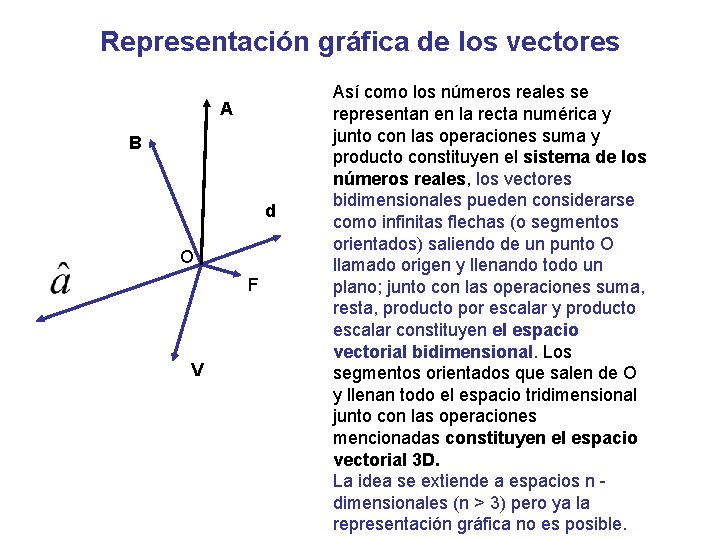
Representación gráfica de los vectores A B d O F V Así como los números reales se representan en la recta numérica y junto con las operaciones suma y producto constituyen el sistema de los números reales, los vectores bidimensionales pueden considerarse como infinitas flechas (o segmentos orientados) saliendo de un punto O llamado origen y llenando todo un plano; junto con las operaciones suma, resta, producto por escalar y producto escalar constituyen el espacio vectorial bidimensional. Los segmentos orientados que salen de O y llenan todo el espacio tridimensional junto con las operaciones mencionadas constituyen el espacio vectorial 3 D. La idea se extiende a espacios n dimensionales (n > 3) pero ya la representación gráfica no es posible.

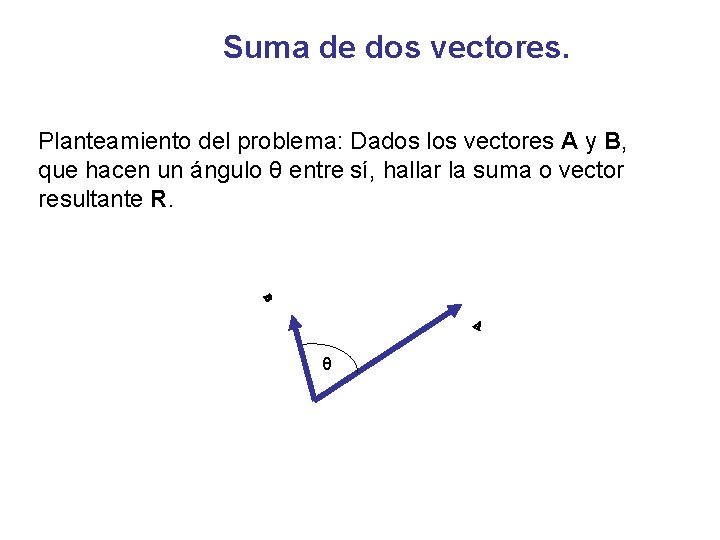
Suma de dos vectores. Planteamiento del problema: Dados los vectores A y B, que hacen un ángulo θ entre sí, hallar la suma o vector resultante R. θ

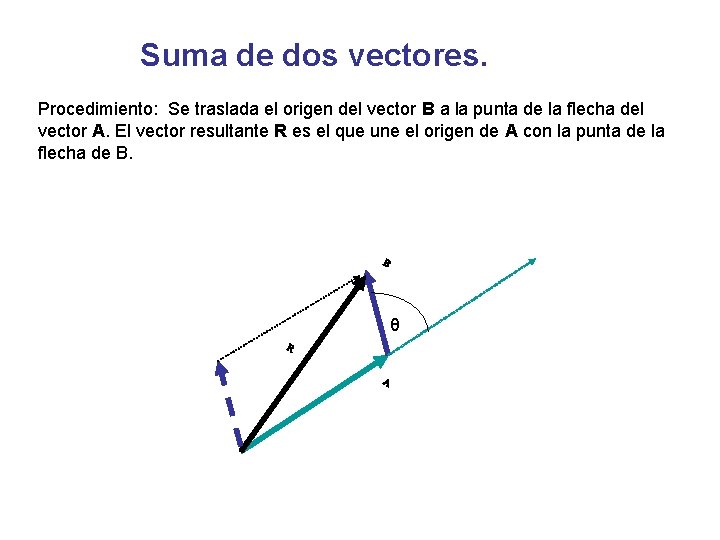
Suma de dos vectores. Procedimiento: Se traslada el origen del vector B a la punta de la flecha del vector A. El vector resultante R es el que une el origen de A con la punta de la flecha de B. θ

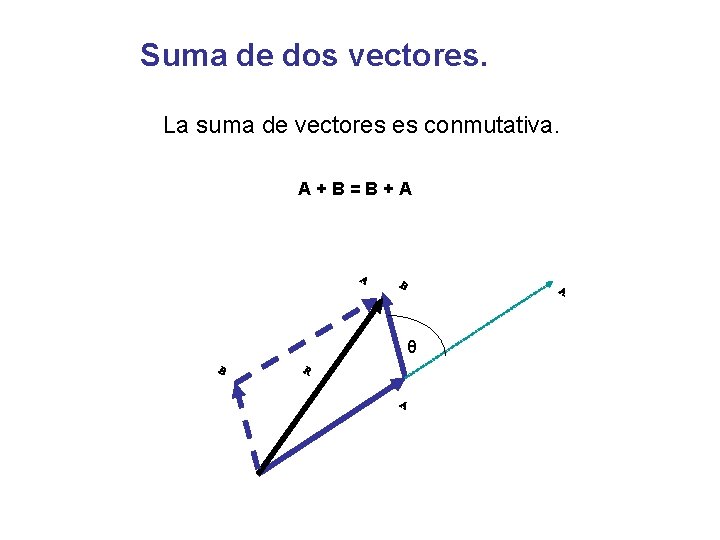
Suma de dos vectores. La suma de vectores es conmutativa. A+B=B+A θ

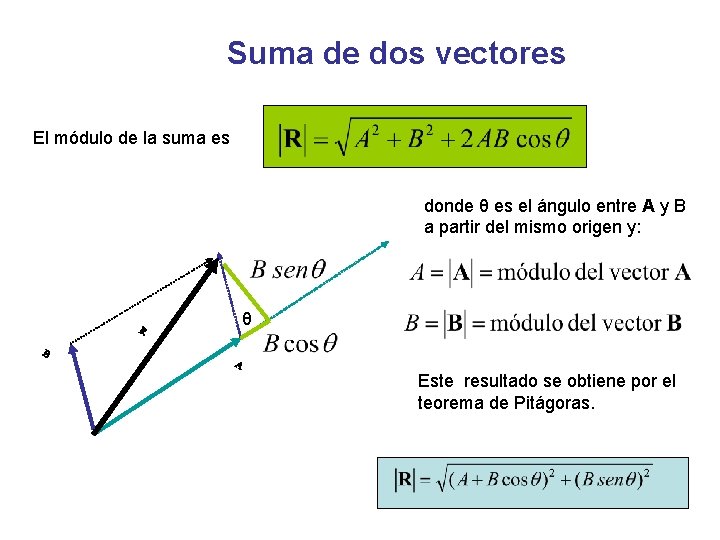
Suma de dos vectores El módulo de la suma es donde θ es el ángulo entre A y B a partir del mismo origen y: θ Este resultado se obtiene por el teorema de Pitágoras.

Suma de varios vectores. R=A+B+C C B A El vector resultante R es el que une el origen de A con la punta de la flecha de C. A + (B+ C) = (A + B)+ C = A + B+ C

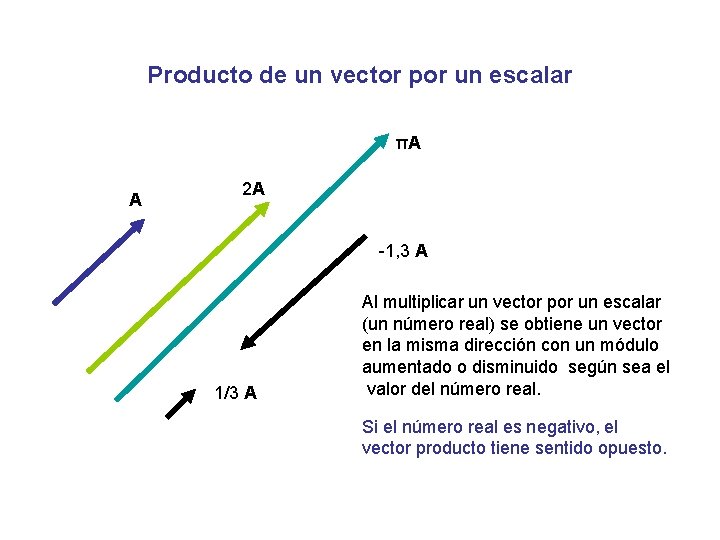
Producto de un vector por un escalar πA A 2 A -1, 3 A 1/3 A Al multiplicar un vector por un escalar (un número real) se obtiene un vector en la misma dirección con un módulo aumentado o disminuido según sea el valor del número real. Si el número real es negativo, el vector producto tiene sentido opuesto.

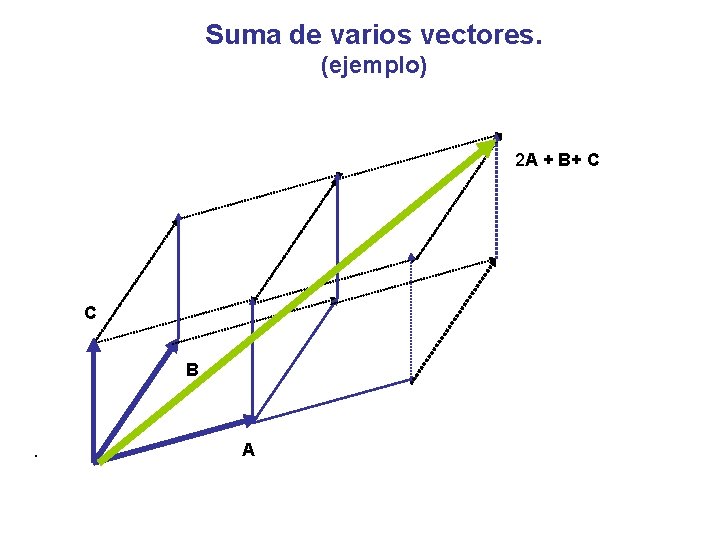
Suma de varios vectores. (ejemplo) 2 A + B+ C C B . A

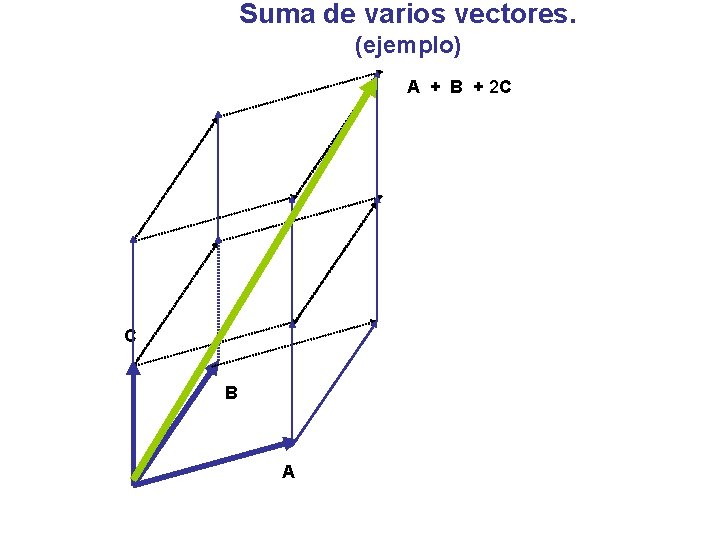
Suma de varios vectores. (ejemplo) A + B + 2 C C B A

Resta de vectores. B θ Hallar D = A - B A B Procedimiento: Se multiplica B por -1 y se procede a sumar A + ( -B) θ Π -B A -θ D

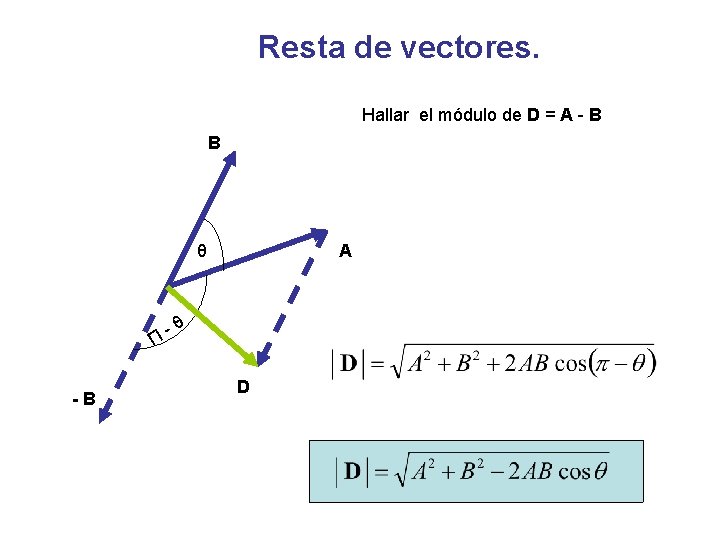
Resta de vectores. Hallar el módulo de D = A - B B θ Π -B A -θ D

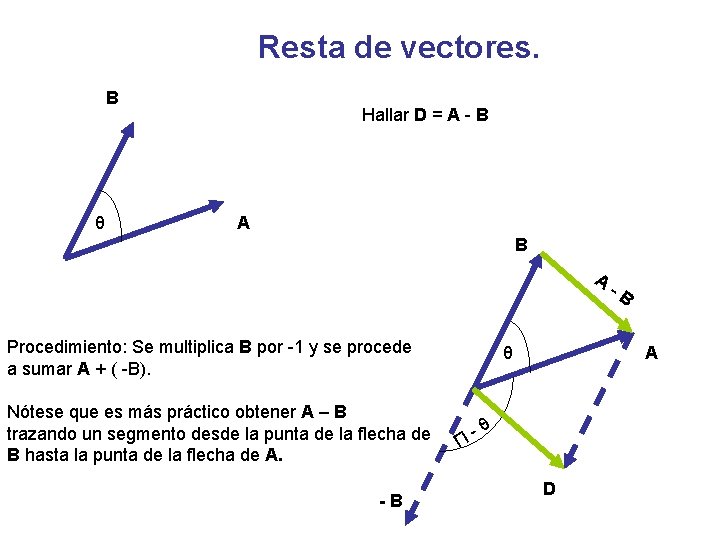
Resta de vectores. B θ Hallar D = A - B A Procedimiento: Se multiplica B por -1 y se procede a sumar A + ( -B). Nótese que es más práctico obtener A – B trazando un segmento desde la punta de la flecha de B hasta la punta de la flecha de A. -B θ Π -B A -θ D

Operaciones combinadas. Ejercicio: Escriba los signos y coeficientes correctos en las expresiones: V 1 = A – 2 B + C y V 2 = 2 A – B + C V 1 C B V 2 A

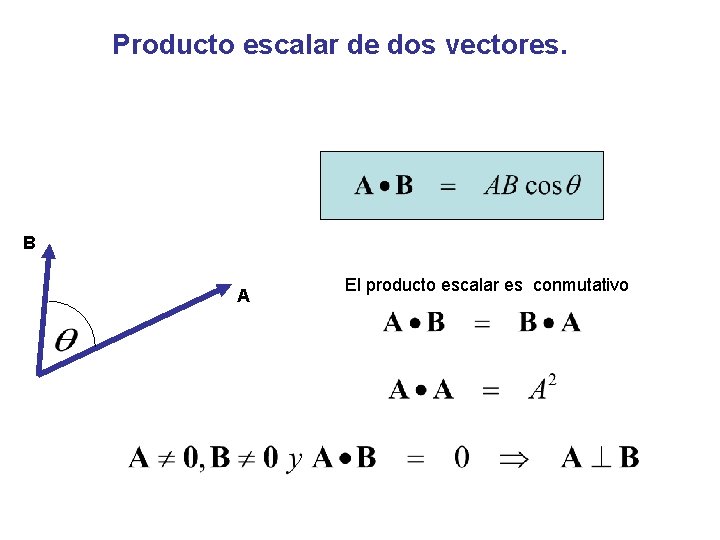
Producto escalar de dos vectores. B A El producto escalar es conmutativo

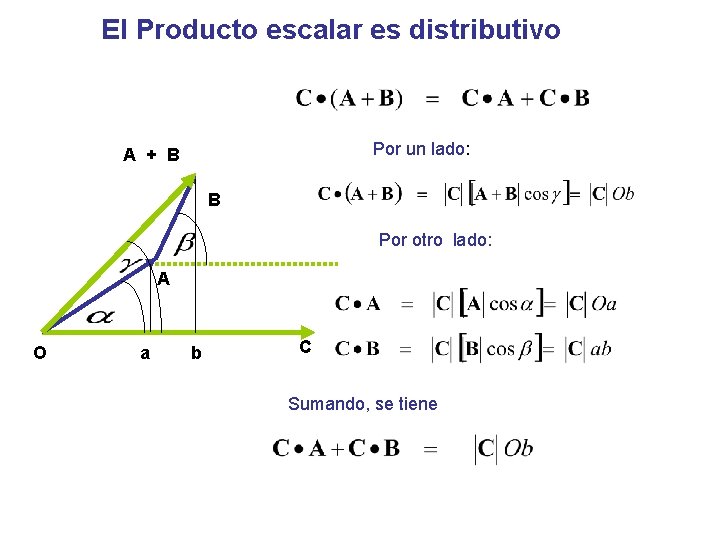
El Producto escalar es distributivo Por un lado: A + B B Por otro lado: A O a b C Sumando, se tiene

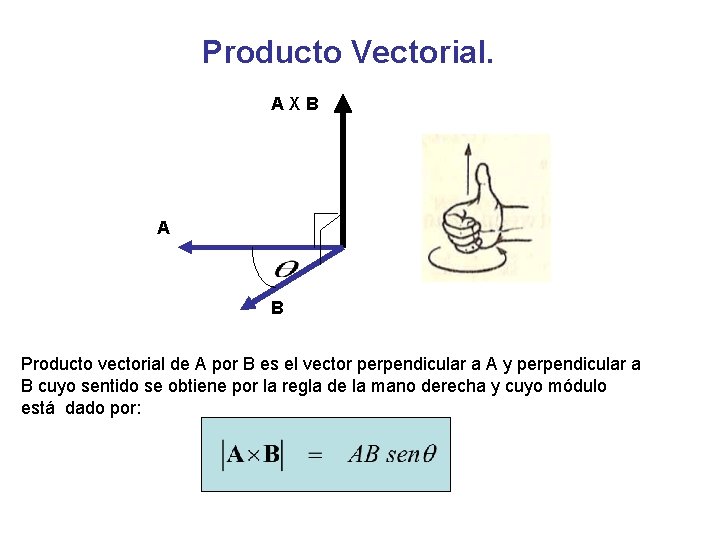
Producto Vectorial. AXB A B Producto vectorial de A por B es el vector perpendicular a A y perpendicular a B cuyo sentido se obtiene por la regla de la mano derecha y cuyo módulo está dado por:

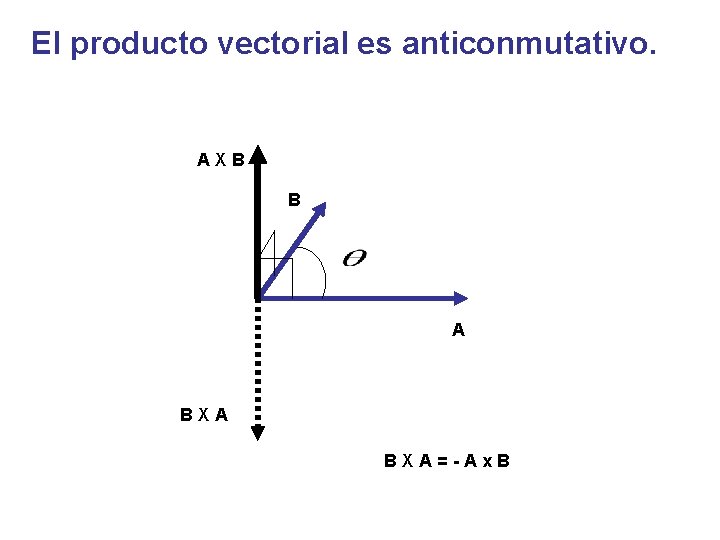
El producto vectorial es anticonmutativo. AXB B A BXA=-Ax. B

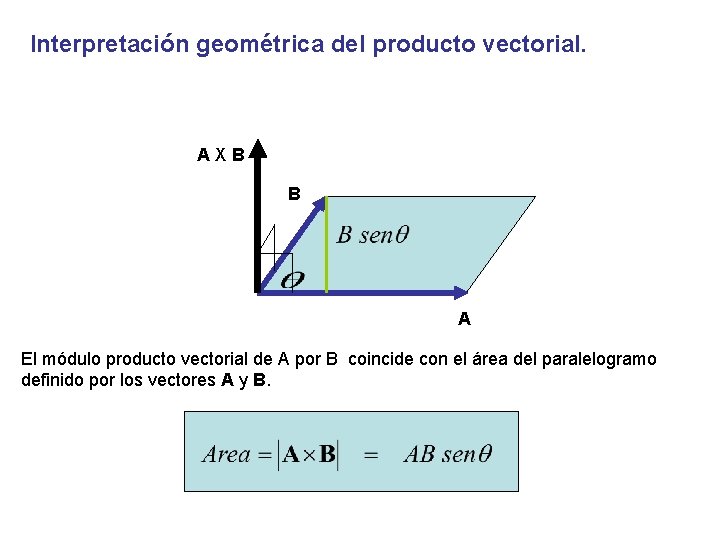
Interpretación geométrica del producto vectorial. AXB B A El módulo producto vectorial de A por B coincide con el área del paralelogramo definido por los vectores A y B.

El producto vectorial es distributivo. A + B b B Por un lado: a A Por otro lado: O C Sumando, se tiene

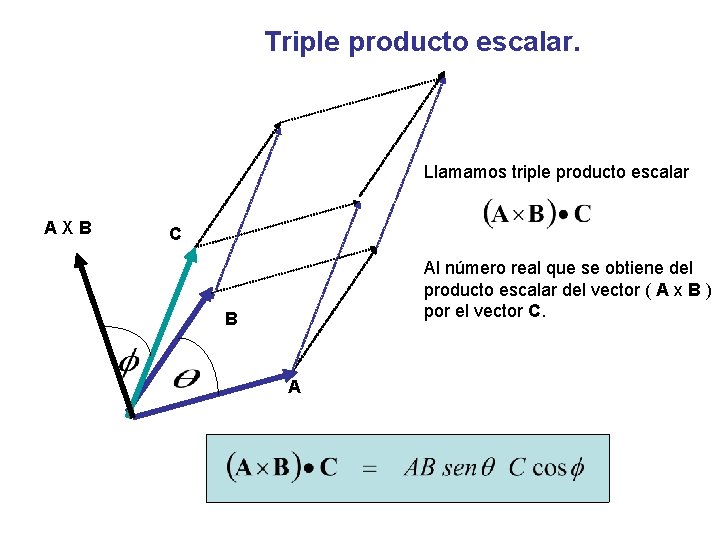
Triple producto escalar. Llamamos triple producto escalar AXB C Al número real que se obtiene del producto escalar del vector ( A x B ) por el vector C. B A

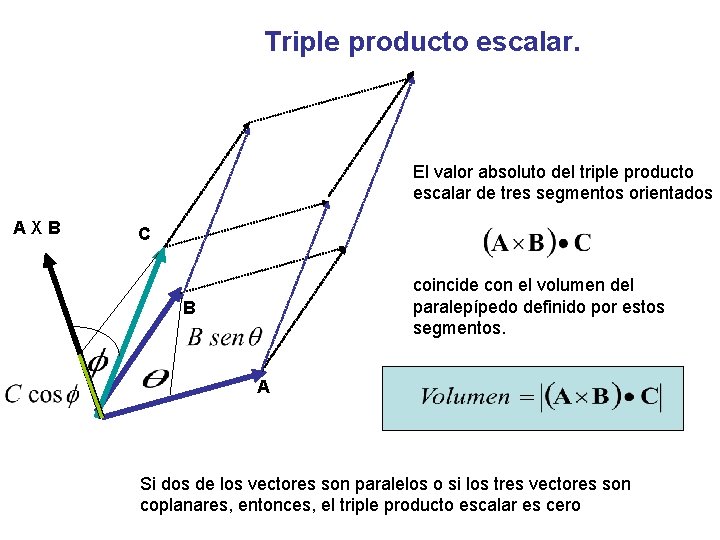
Triple producto escalar. El valor absoluto del triple producto escalar de tres segmentos orientados AXB C coincide con el volumen del paralepípedo definido por estos segmentos. B A Si dos de los vectores son paralelos o si los tres vectores son coplanares, entonces, el triple producto escalar es cero

Vector unitario. Dado un vector A, entonces, el vector A u es un vector unitario en la dirección y sentido de A Un vector unitario es un vector sin unidades cuyo módulo es uno y sólo se usa para especificar una dirección

Vector unitario. A u. B B Cualquier vector puede ser expresado como el producto de un número real por un vector unitario

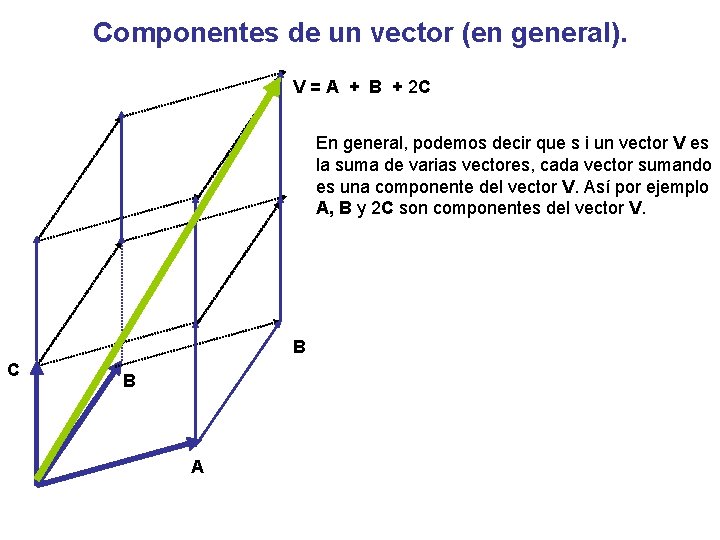
Componentes de un vector (en general). V = A + B + 2 C En general, podemos decir que s i un vector V es la suma de varias vectores, cada vector sumando es una componente del vector V. Así por ejemplo A, B y 2 C son componentes del vector V. B C B A

Componentes de un vector. Nos interesa estudiar el concepto de componentes de un vector en dos situaciones: Situación 1: Dados vectores A y V, expresar el vector A como la suma de dos vectores: uno paralelo a V y otro perpendicular a V. Situación 2: Definir tres (dos) vectores mutuamente perpendiculares: i, j, k y expresar cualquier vector A como la suma de tres (dos) vectores paralelos a i, j y k ( i y j).

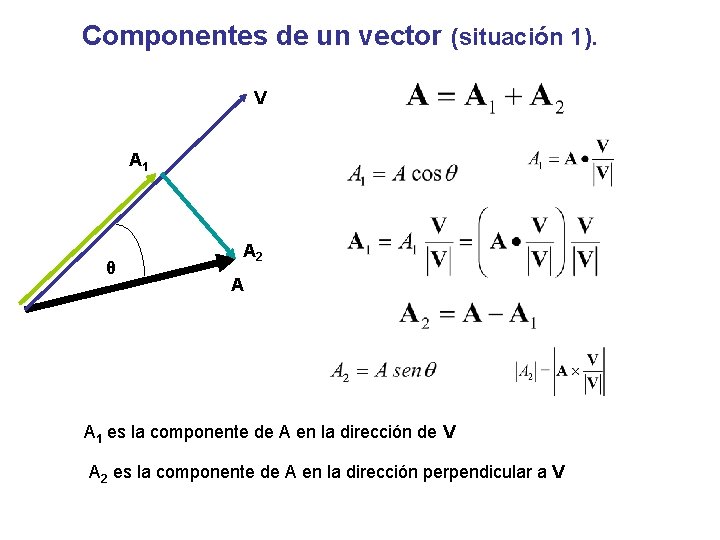
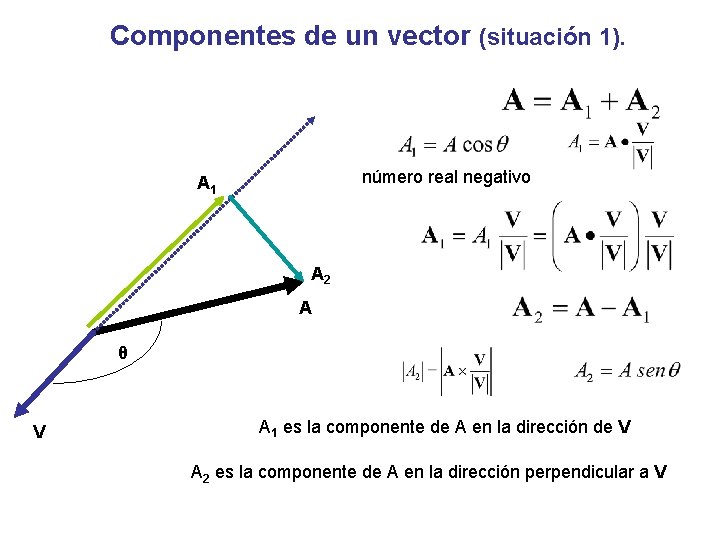
Componentes de un vector (situación 1). V A 1 θ A 2 A A 1 es la componente de A en la dirección de V A 2 es la componente de A en la dirección perpendicular a V

Componentes de un vector (situación 1). número real negativo A 1 A 2 A θ V A 1 es la componente de A en la dirección de V A 2 es la componente de A en la dirección perpendicular a V

Componentes de un vector (situación 1). V A 1 θ A 2 A

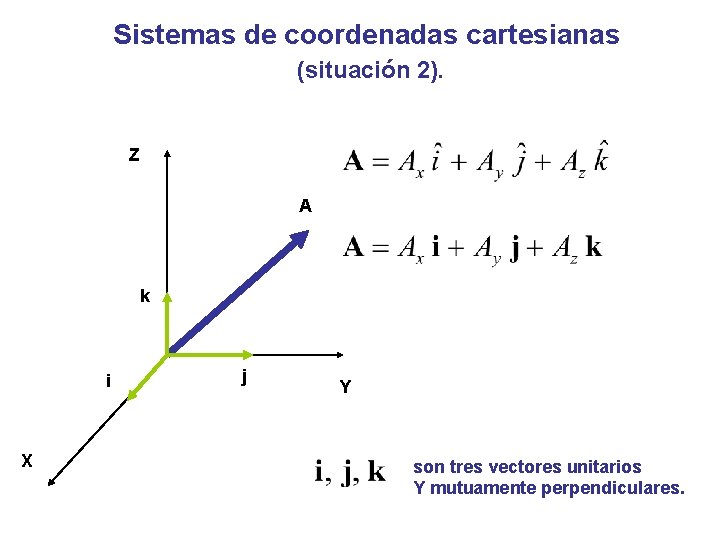
Sistemas de coordenadas cartesianas (situación 2). Z A k i X j Y son tres vectores unitarios Y mutuamente perpendiculares.

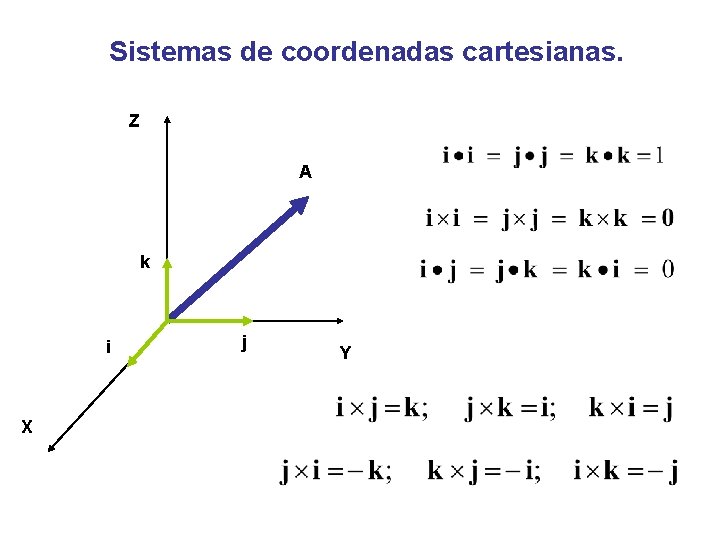
Sistemas de coordenadas cartesianas. Z A k i X j Y

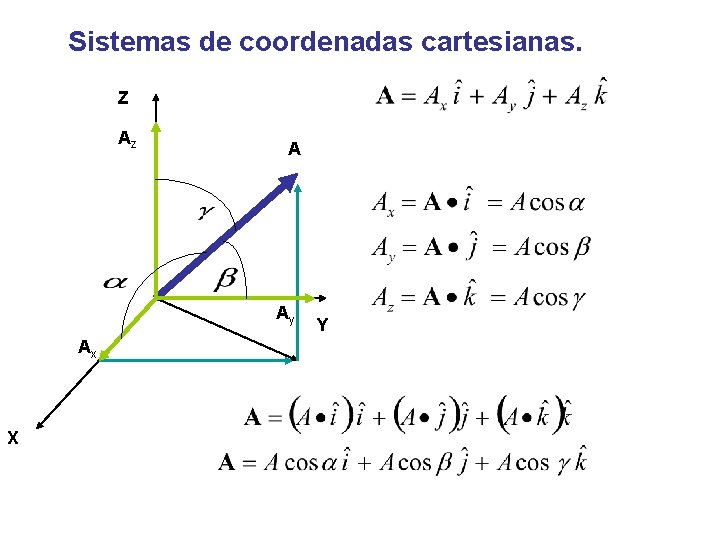
Sistemas de coordenadas cartesianas. Z Az A Ay Ax X Y

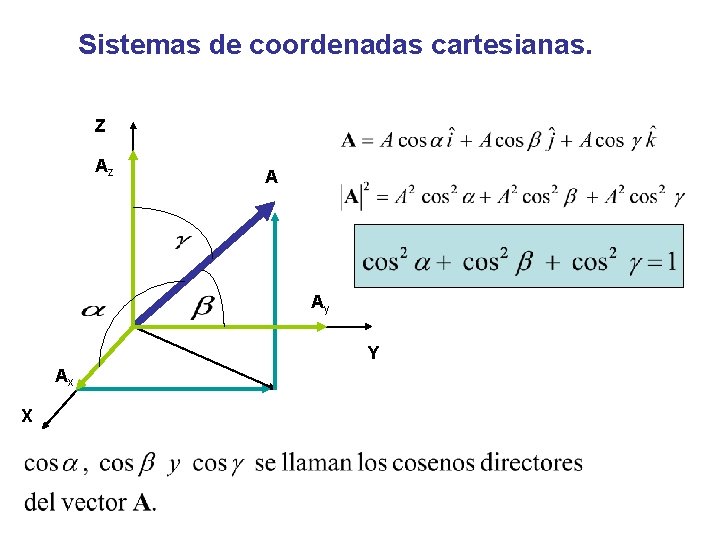
Sistemas de coordenadas cartesianas. Z Az A Ay Y Ax X

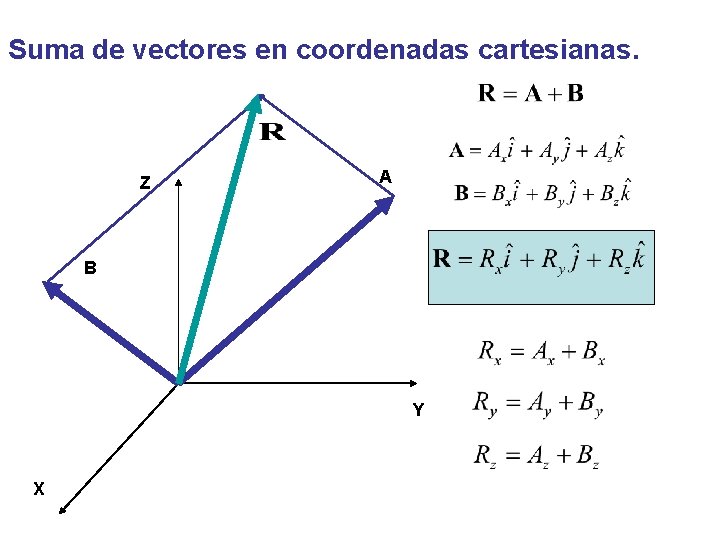
Suma de vectores en coordenadas cartesianas. Z A B Y X

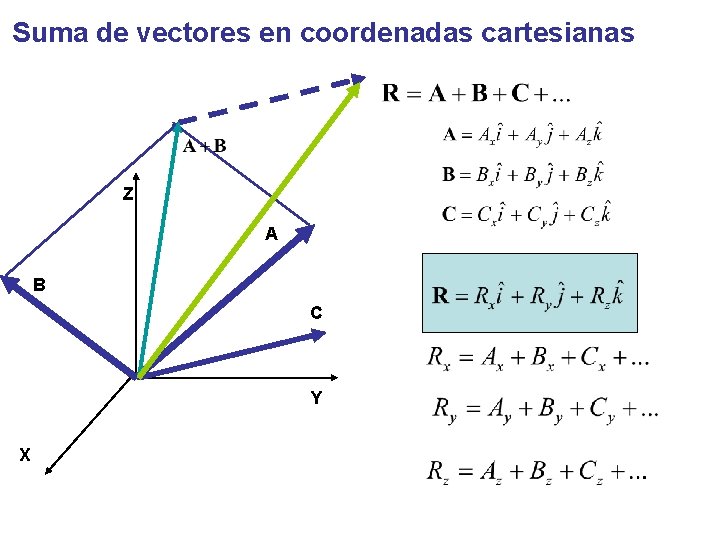
Suma de vectores en coordenadas cartesianas Z A B C Y X

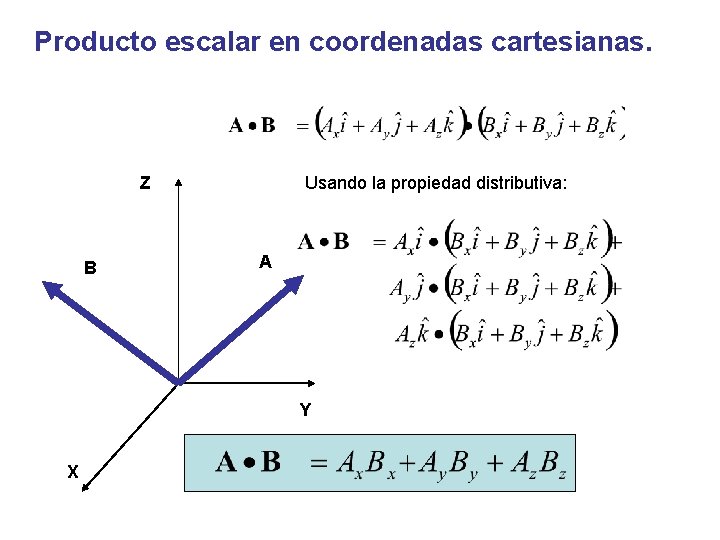
Producto escalar en coordenadas cartesianas. Z B Usando la propiedad distributiva: A Y X

Producto vectorial en coordenadas cartesianas. Z A B Usando la propiedad distributiva Y X

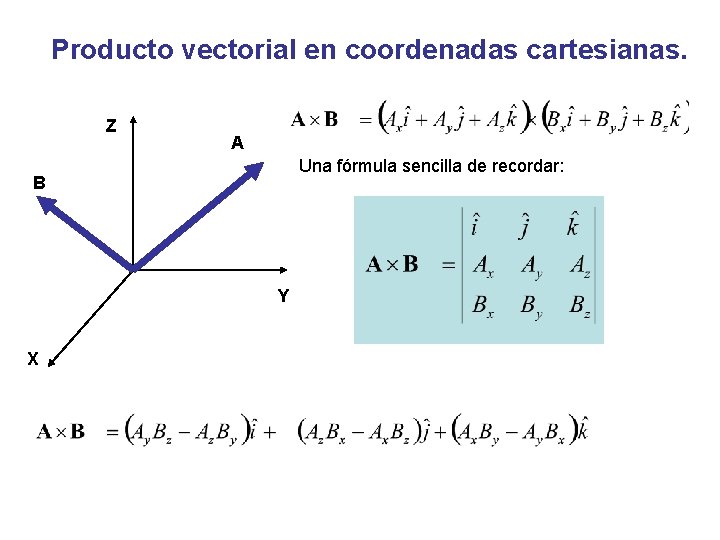
Producto vectorial en coordenadas cartesianas. Z A Una fórmula sencilla de recordar: B Y X

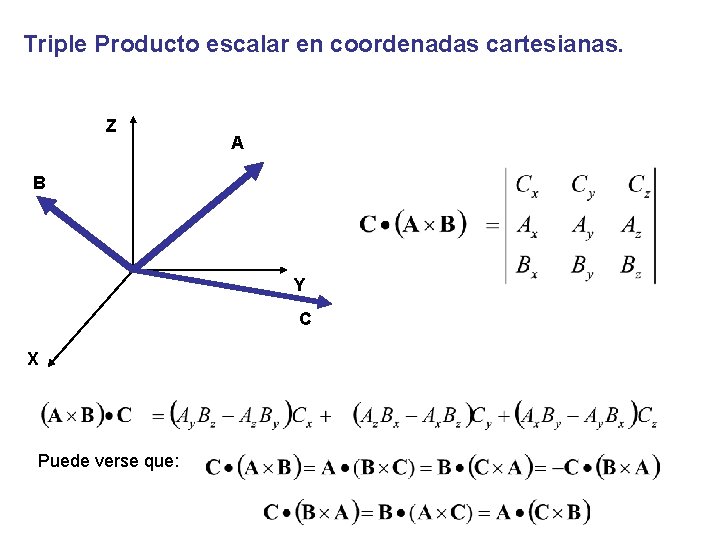
Triple Producto escalar en coordenadas cartesianas. Z A B Y C X Puede verse que:

Triple producto vectorial A x (B X C). Fuente: INTRODUCCIÓN A LA FÍSICA MATEMÁTICA. Departamento de Física, Facultad de Ciencias, Universidad de Chile.

Triple producto vectorial A x (B X C). El triple producto vectorial A x (B X C), es un vector

FIN