FILTRATION Introduction Filtration may be defined as the

FILTRATION

Introduction Filtration may be defined as the separation of solids from liquids by passing a suspension through a permeable medium which retains the particles. Figure 1. Schematic diagram of filtration system

The fine apertures necessary for filtration are provided Ø by fabric filter cloths, Ø by meshes and screens of plastics or metals, Ø by beds of solid particles. In some cases, a thin preliminary coat of cake, or of other fine particles, is put on the cloth prior to the main filtration process.

Types of filtration 1. Surface filters 2. Depth filters

1. Surface filters used for cake filtration in which the solids are deposited in the form of a cake on the up-stream side of a relatively thin filter medium. Figure 2. Mechanism of cake filtration

2. Depth filters used for deep bed filtration in which particle deposition takes place inside the medium and cake deposition on the surface is undesirable. Figure 3. Mechanism of deep bed filtration

The fluid passes through the filter medium, which offers resistance to its passage, under the influence of a force which is the pressure differential across the filter. rate of filtration = driving force/resistance

The filter-cake resistance is obtained by multiplying the specific resistance of the filter cake, that is its resistance per unit thickness, by the thickness of the cake. The resistances of the filter material and precoat are combined into a single resistance called the filter resistance. It is convenient to express the filter resistance in terms of a fictitious thickness of filter cake. This thickness is multiplied by the specific resistance of the filter cake to give the filter resistance.

Filtration Equipment The basic requirements for filtration equipment are: mechanical support for the filter medium flow accesses to and from the filter medium provision for removing excess filter cake.

In some instances, washing of the filter cake to remove traces of the solution may be necessary. Pressure can be provided on the upstream side of the filter, or a vacuum can be drawn downstream, or both can be used to drive the wash fluid through.

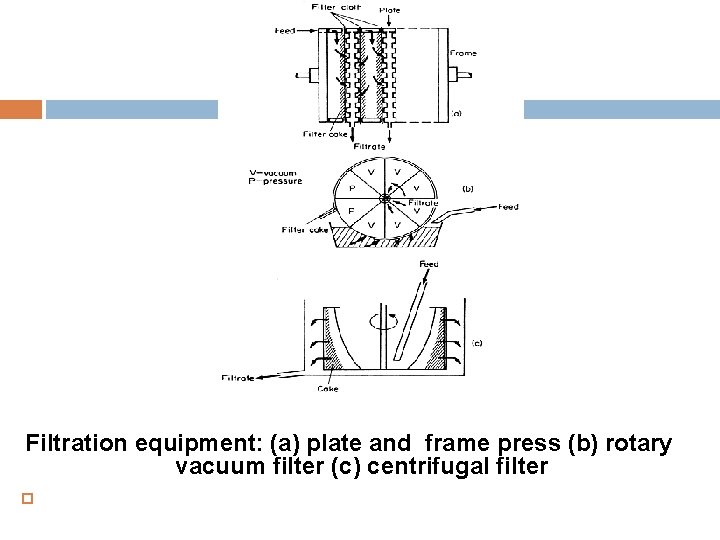
Filtration equipment: (a) plate and frame press (b) rotary vacuum filter (c) centrifugal filter

1. Plate and frame filter press In the plate and frame filter press, a cloth or mesh is spread out over plates which support the cloth along ridges but at the same time leave a free area, as large as possible, below the cloth for flow of the filtrate. The plates with their filter cloths may be horizontal, but they are more usually hung vertically with a number of plates operated in parallel to give sufficient area.

In the early stages of the filtration cycle, the pressure drop across the cloth is small and filtration proceeds at more or less a constant rate. As the cake increases, the process becomes more and more a constant-pressure one and this is the case throughout most of the cycle. When the available space between successive frames is filled with cake, the press has to be dismantled and the cake scraped off and cleaned, after which a further cycle can be initiated.

The plate and frame filter press is cheap but it is difficult to mechanize to any great extent. Filtration can be done under pressure or vacuum. The advantage of vacuum filtration is that the pressure drop can be maintained whilst the cake is still under atmospheric pressure and so can be removed easily. The disadvantages are the greater costs of maintaining a given pressure drop by applying a vacuum and the limitation on the vacuum to about 80 k. Pa maximum. In pressure filtration, the pressure driving force is limited only by the economics of attaining the pressure and by the mechanical strength of the equipment

BAS stainless steel plate and frame filter press

2. Rotary filters In rotary filters, the flow passes through a rotating cylindrical cloth from which the filter cake can be continuously scraped. Either pressure or vacuum can provide the driving force, but a particularly useful form is the rotary vacuum filter.

The rotary vacuum drum filter

A suitable bearing applies the vacuum at the stage where the actual filtration commences and breaks the vacuum at the stage where the cake is being scraped off after filtration. Filtrate is removed through trunnion bearings. Rotary vacuum filters are expensive, but they do provide a considerable degree of mechanization and convenience.

3. Centrifugal filters Centrifugal force is used to provide the driving force in some filters. These machines are really centrifuges fitted with a perforated bowl that may also have filter cloth on it. Liquid is fed into the interior of the bowl and under the centrifugal forces, it passes out through the filter material.

Centrifugal filters

4. Air filters Filters are used quite extensively to remove suspended dust or particles from air streams. The air or gas moves through a fabric and the dust is left behind. These filters are particularly useful for the removal of fine particles. The air passing through the bags in parallel. Air bearing the dust enters the bags, usually at the bottom and the air passes out through the cloth

A familiar example of a bag filter for dust is to be found in the domestic vacuum cleaner. Some designs of bag filters provide for the mechanical removal of the accumulated dust.

Factor affected on filtration Pressure drop ( ∆P( Area of filtering surface ( A ) Viscosity of filtrate ( v ) Resistance of filter cake ( α( Resistance of filter medium ( Rm( Properties of slurry ( μ , ��� (

-( P) or Pressure drop rate of filtration = driving force/resistance Filter cake ( ) Filter medium (Rm) Viscosity ( )

Filtration Equation Flow of fluid through packed bed : Application of Carman-kozeny’s equation โดย k 1 = = v = = L = S 0 area per (m 2/m 3) Pc = constant = 4. 17 for particles with definite size and shape viscosity of filtrate (Pa. s) linear velocity based on filter area (m/s) void fraction ���� porosity of cake thickness of cake (m) = specific surface area of particle volume of solid particle pressure drop in cake (N/m 2)

Substitute v in term of volume (V) A = filter area (m 2) V = volume of filtrate at t sec L = thickness of filter cake Cs = kg of solid/m 3 of filtrate P = density of solid particle in cake (kg/m 3)

Substitute L in term of height of cake (L) Obtain:

Specific cake resistance ( ) ��� = S 0 = Void fraction specific surface area of particle (m 2)

Specific cake resistance; Their specific resistance change with pressure drop across the cake ∆pc. In such cases, an average specific cake resistance av should can be determine from If the function = (∆pc) is known from pilot filtration tests, bomb filter test or from the use of a compressibility cell.

An experimental empirical relationship can be used over a limit pressure range Where 0 : the resistance at unit applied pressure drop n : a compressibility index obtained from experiments (n = 0 for incompressible substance)

Filter medium resistance; R Normally be constant but may vary with time (as a result of some penetration of solid into the medium) and sometimes may also change with applied pressure (because of the compression of fiber in the medium).

As the overall pressure drop across an installed filter include losses not only in the medium but also in the associated piping and in the inlet and outlet ports It is convenient in practice to include all these extra resistances in the value of the medium resistance R.

Constant pressure filtration Equation is useful because it covers a situation that is frequently found in a practical filtration plant. We could predict the performance of filtration plant on the basis of experimental results. If a test is carried out using constant pressure, collecting and measuring the filtrate at measured time intervals

Filtration Equations for Constant – Pressure Filtration

At At tt == tt sec

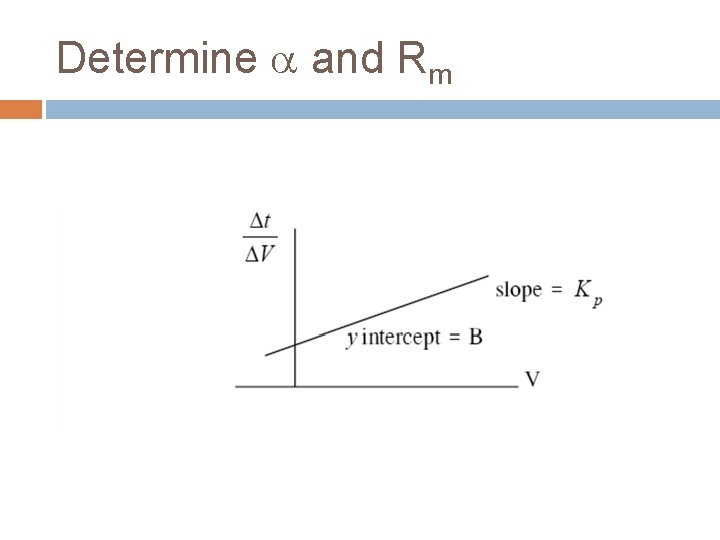
Determine and Rm

Filtration equation for Constant rate Filtration

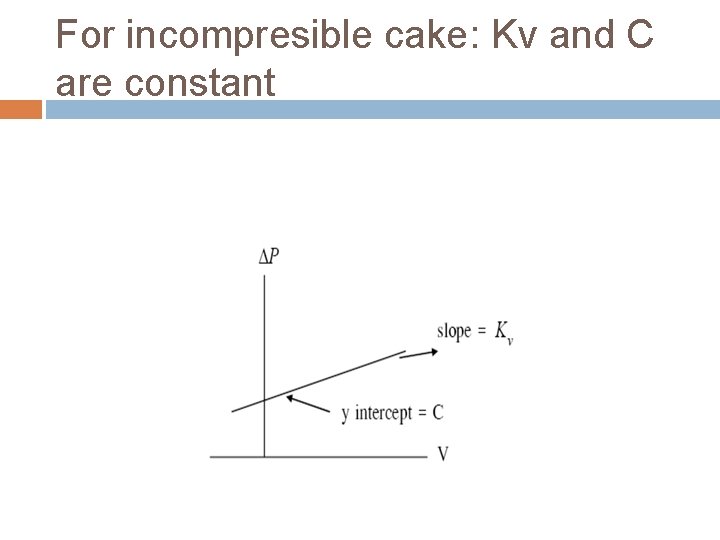
For incompresible cake: Kv and C are constant

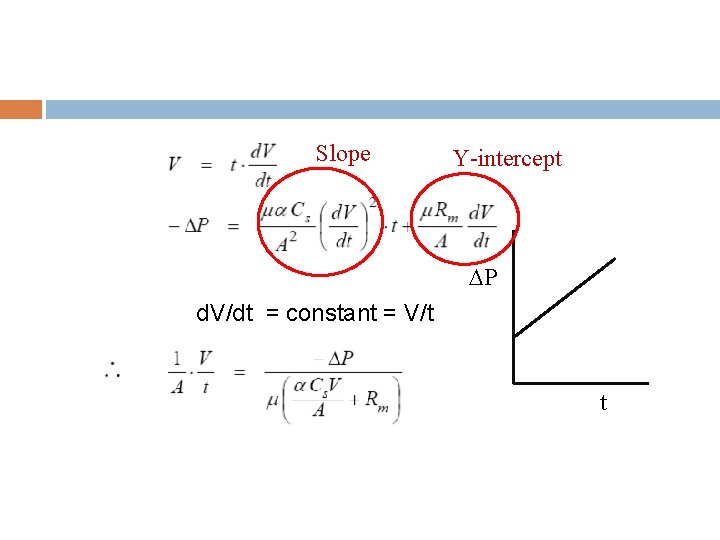
Slope Y-intercept P d. V/dt = constant = V/t t

From constant rate equation the pressure drop required for any desired flow rate can be found. Also, if a series of runs is carried out under different pressures, the results can be used to determine the resistance of the filter cake.

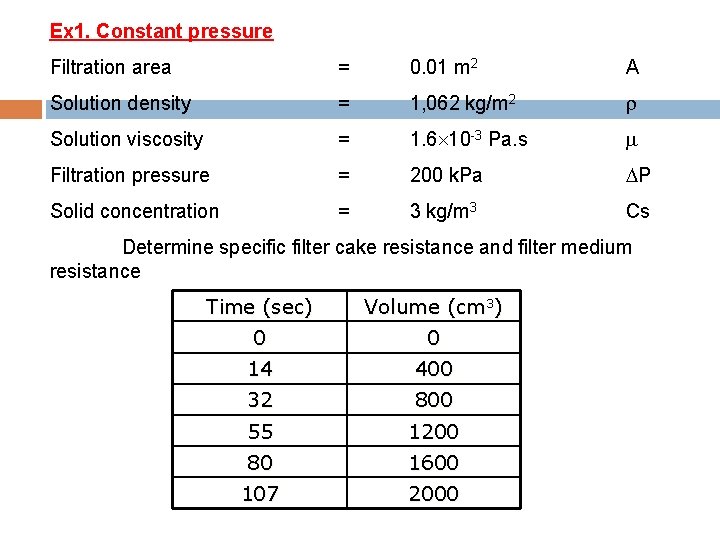
Ex 1. Constant pressure Filtration area = 0. 01 m 2 A Solution density = 1, 062 kg/m 2 Solution viscosity = 1. 6 10 -3 Pa. s Filtration pressure = 200 k. Pa P Solid concentration = 3 kg/m 3 Cs Determine specific filter cake resistance and filter medium resistance Time (sec) Volume (cm 3) 0 0 14 400 32 800 55 1200 80 1600 107 2000

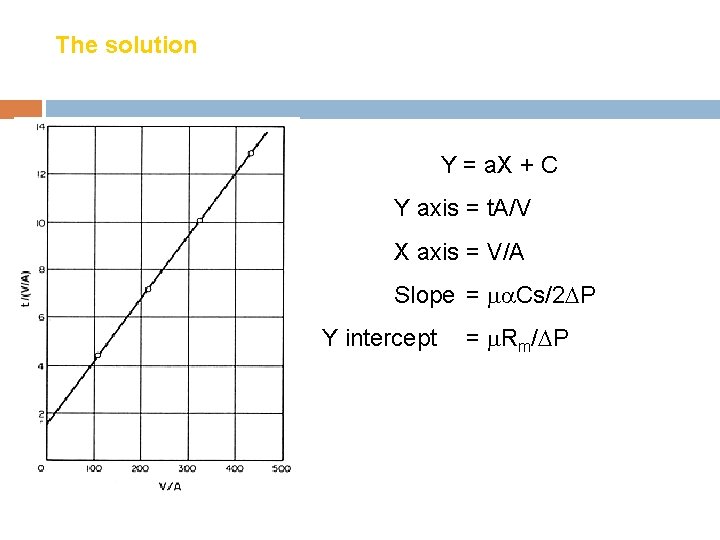
The solution Y = a. X + C Y axis = t. A/V X axis = V/A Slope = Cs/2 P Y intercept = Rm/ P

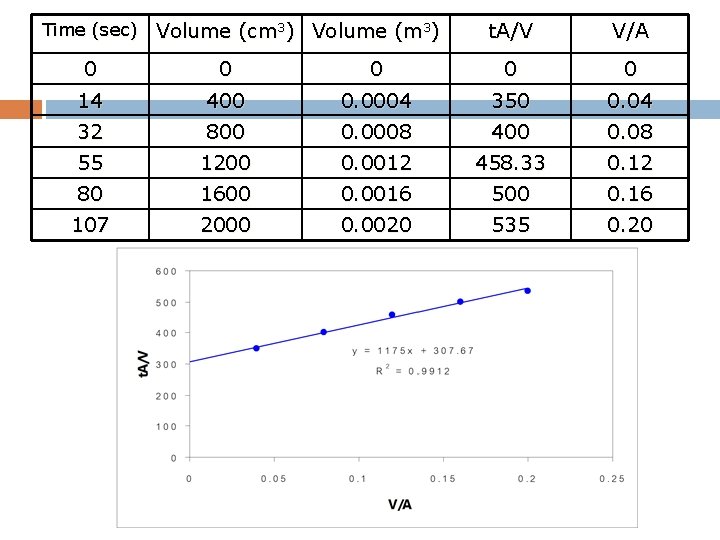
Time (sec) Volume (cm 3) Volume (m 3) t. A/V V/A 0 0 0 14 400 0. 0004 350 0. 04 32 800 0. 0008 400 0. 08 55 1200 0. 0012 458. 33 0. 12 80 1600 0. 0016 500 0. 16 107 2000 0. 0020 535 0. 20

Ex 2. Constant rate A slurry containing 25. 7 kg dry solids/m 3 of filtrate across the filter medium area 2. 15 m 2 at a constant rate of 0. 00118 m 3/s. If the pressure drop was observed 4, 000 and 8, 500 Pa after 150 and 450 seconds of filtration, respectively. The viscosity of filtrate was 0. 001 Pa. s Determine the specific cake resistance and filter medium resistance.

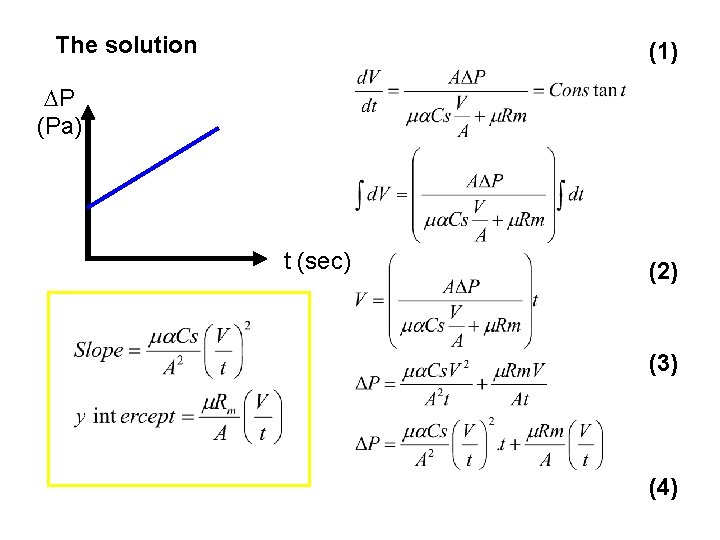
The solution (1) P (Pa) t (sec) (2) (3) (4)

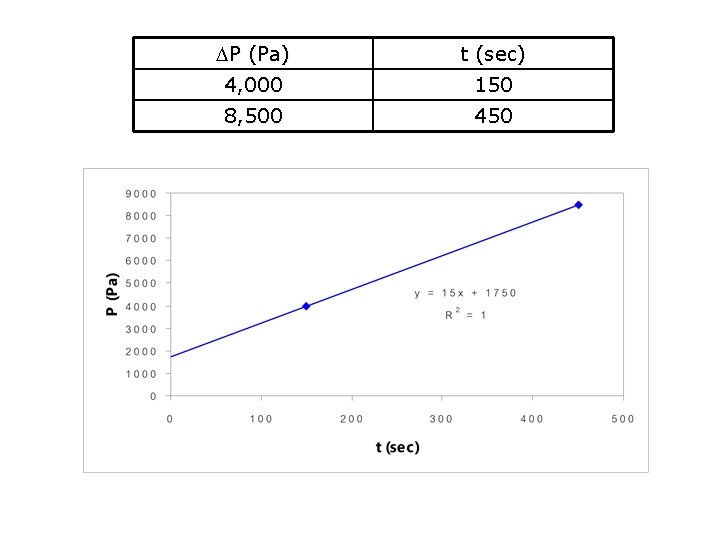
P (Pa) t (sec) 4, 000 150 8, 500 450