Filtering Problem Goal design a filter to attenuate

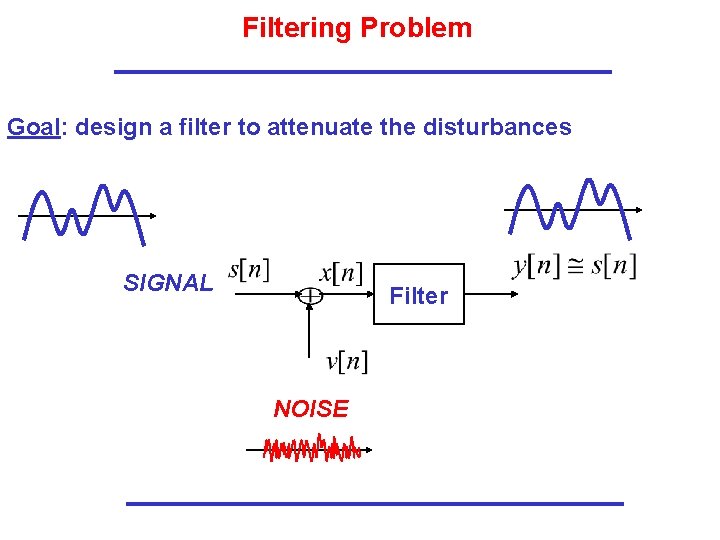
Filtering Problem Goal: design a filter to attenuate the disturbances SIGNAL Filter NOISE

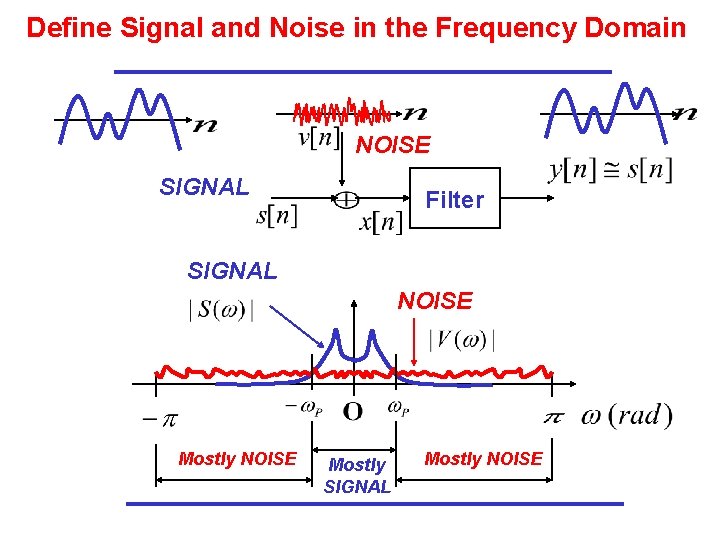
Define Signal and Noise in the Frequency Domain NOISE SIGNAL Filter SIGNAL NOISE Mostly SIGNAL Mostly NOISE

IDEAL Filter Since the filter has real coefficients, we need only the positive frequencies PASS Band STOP Band

Non-IDEAL Filter Since the filter has real coefficients, we need only the positive frequencies PASS Band STOP Band Trans. Band

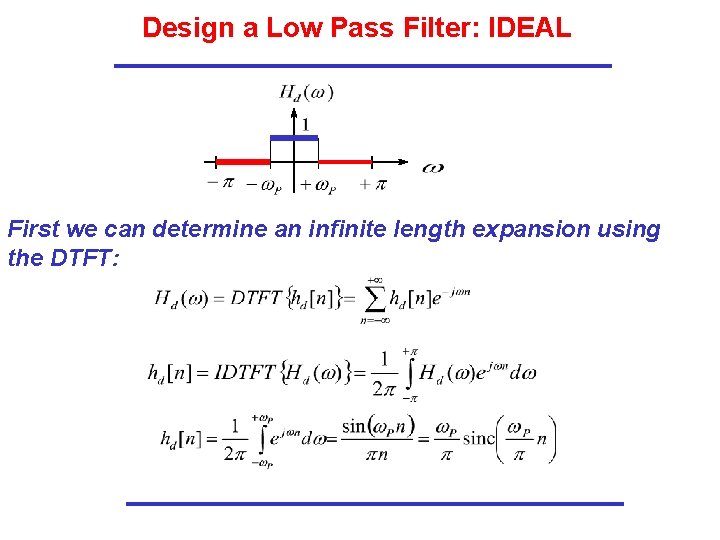
Design a Low Pass Filter: IDEAL First we can determine an infinite length expansion using the DTFT:

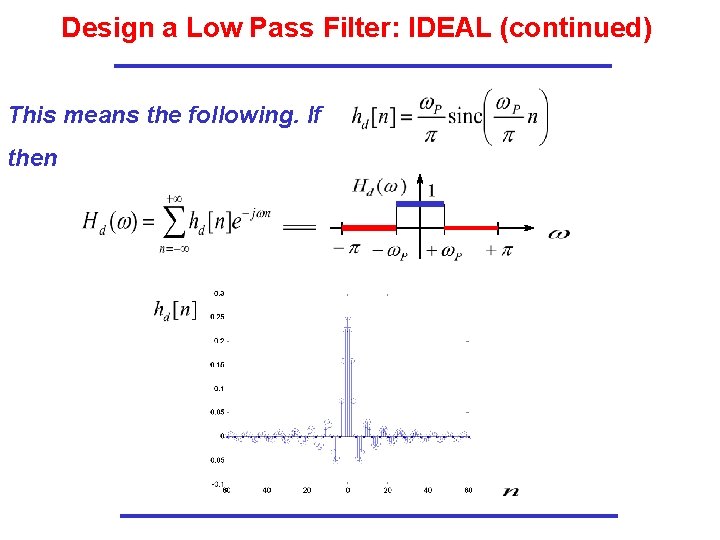
Design a Low Pass Filter: IDEAL (continued) This means the following. If then

From IDEAL to FIR Notice that Then we can approximate with a finite sum… … and choose the filter as actual desired

Summary of design of Low Pass FIR Given the Pass Band Frequency The impulse response of the filter: let Magnitude and Phase: Magnitude: Phase: in the passband

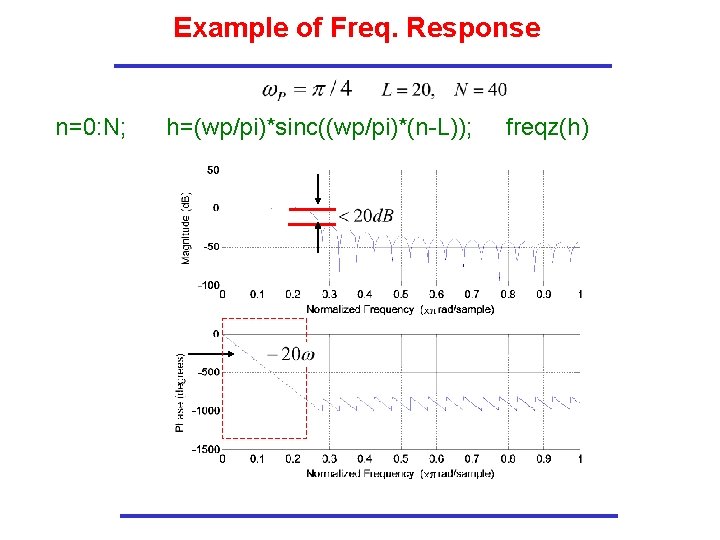
Example of Freq. Response n=0: N; h=(wp/pi)*sinc((wp/pi)*(n-L)); freqz(h)

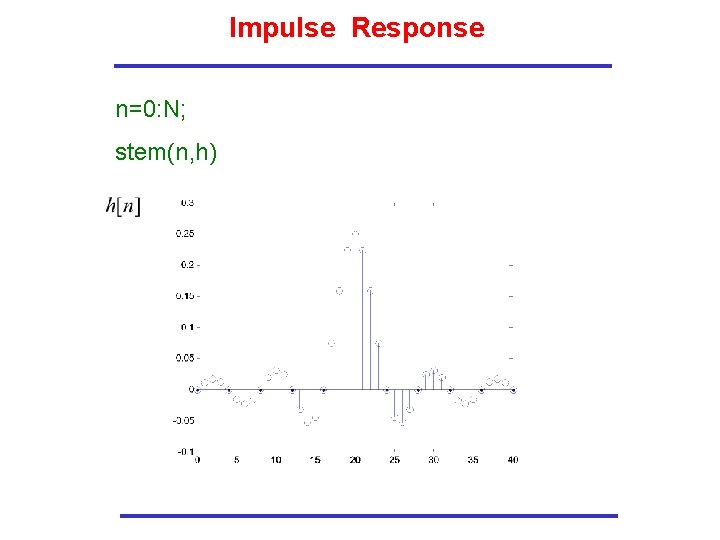
Impulse Response n=0: N; stem(n, h)

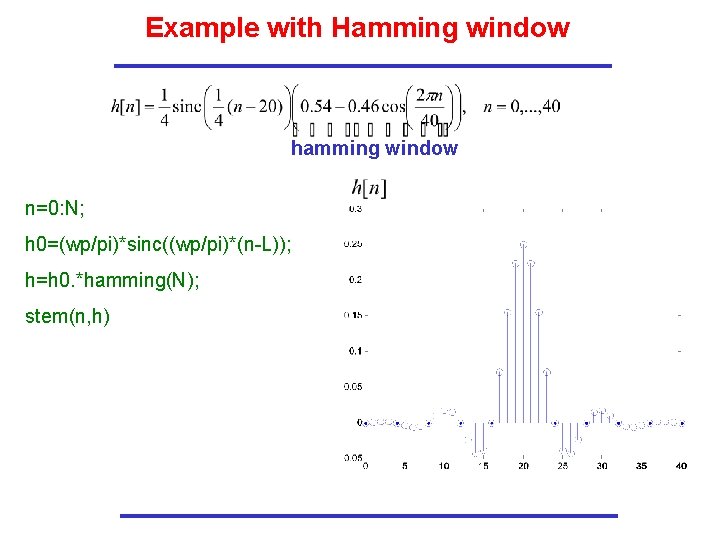
Example with Hamming window hamming window n=0: N; h 0=(wp/pi)*sinc((wp/pi)*(n-L)); h=h 0. *hamming(N); stem(n, h)

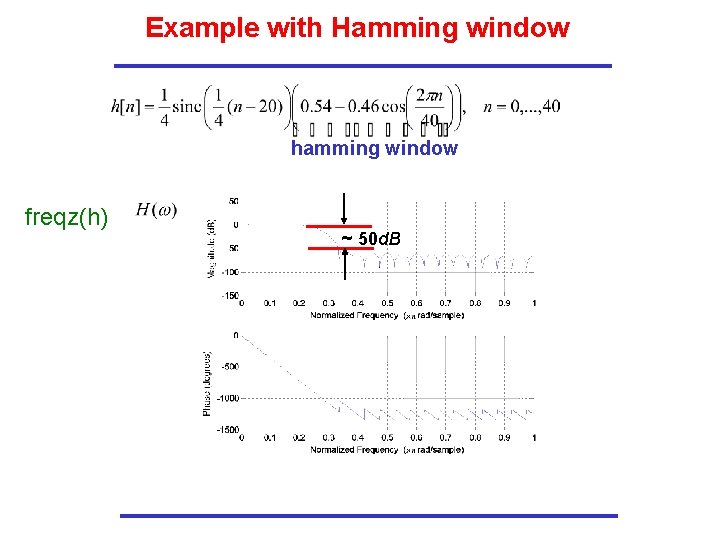
Example with Hamming window hamming window freqz(h) ~ 50 d. B

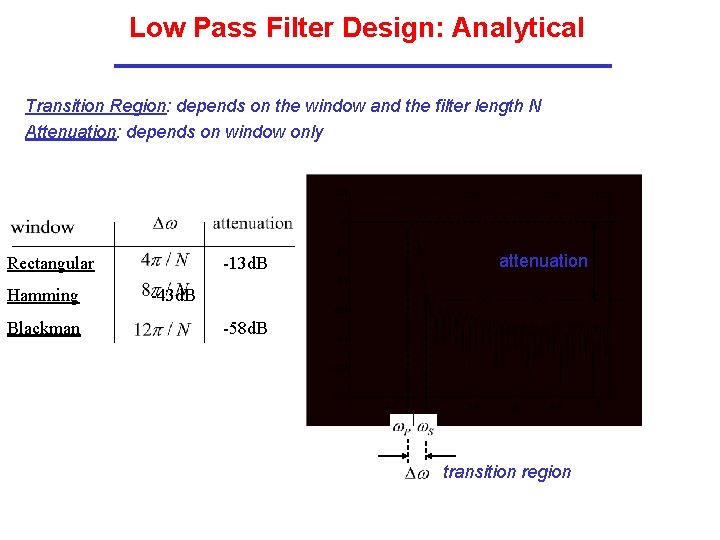
Low Pass Filter Design: Analytical Transition Region: depends on the window and the filter length N Attenuation: depends on window only Rectangular Hamming Blackman -13 d. B attenuation -43 d. B -58 d. B transition region

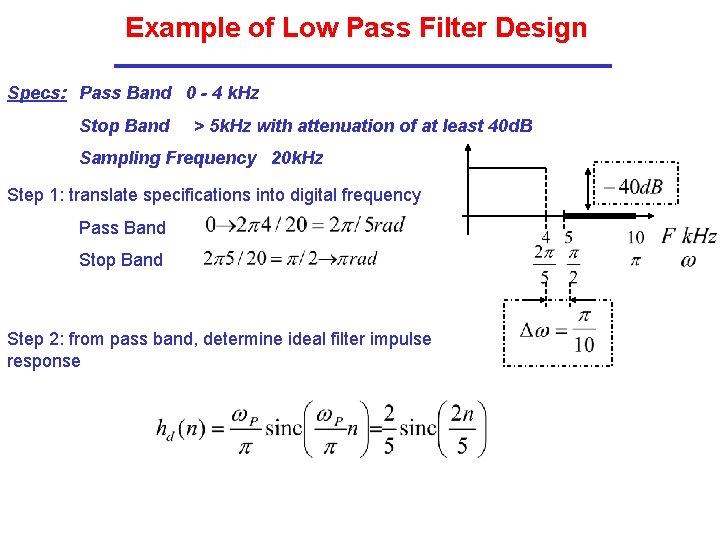
Example of Low Pass Filter Design Specs: Pass Band 0 - 4 k. Hz Stop Band > 5 k. Hz with attenuation of at least 40 d. B Sampling Frequency 20 k. Hz Step 1: translate specifications into digital frequency Pass Band Stop Band Step 2: from pass band, determine ideal filter impulse response

Example of Low Pass Filter Design (continued) Step 3: from desired attenuation choose the window. In this case we can choose the hamming window; Step 4: from the transition region choose the length N of the impulse response. Choose an even number N such that: So choose N=80 which yields the shift L=40.

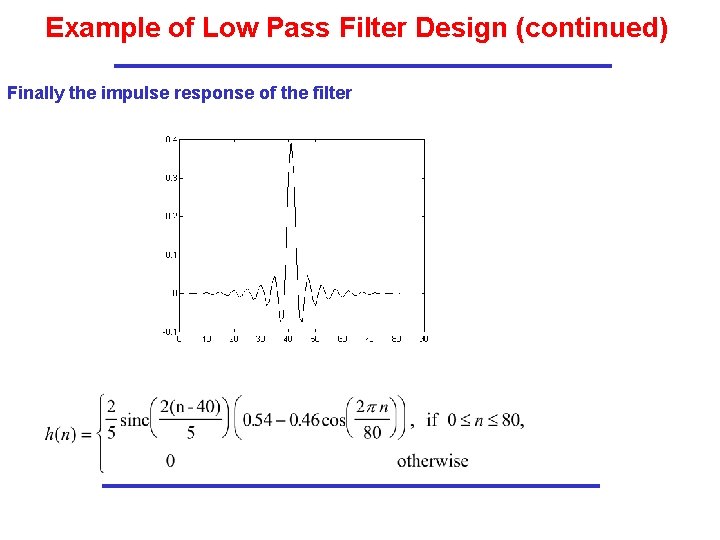
Example of Low Pass Filter Design (continued) Finally the impulse response of the filter

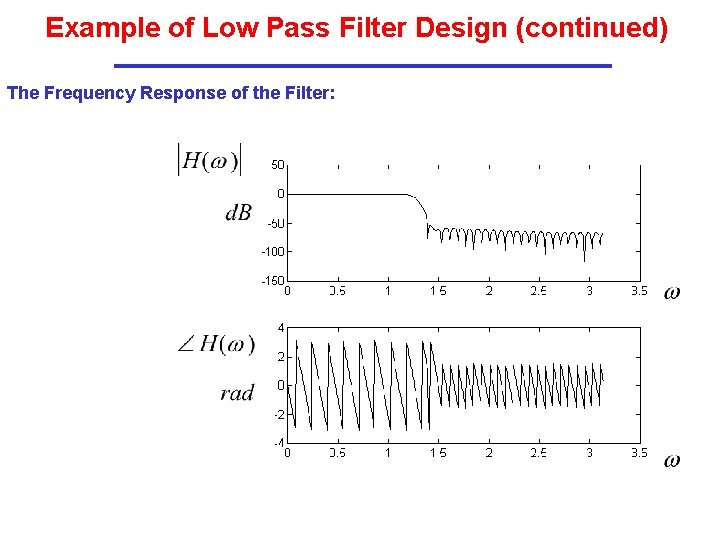
Example of Low Pass Filter Design (continued) The Frequency Response of the Filter:

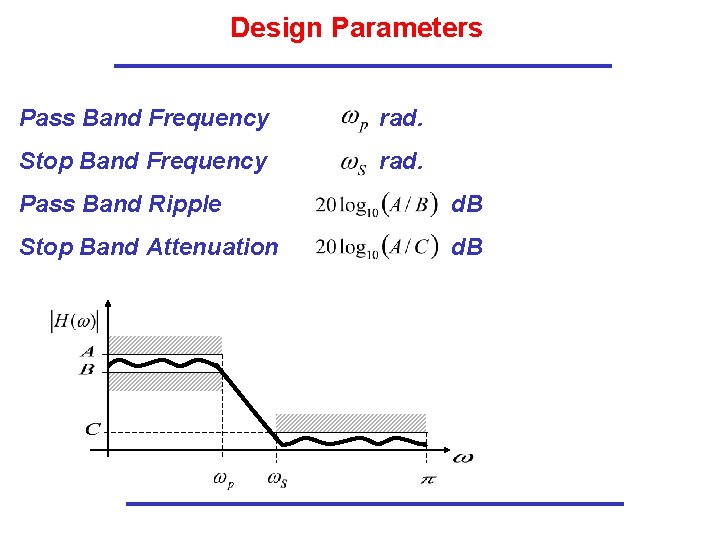
Design Parameters Pass Band Frequency rad. Stop Band Frequency rad. Pass Band Ripple d. B Stop Band Attenuation d. B

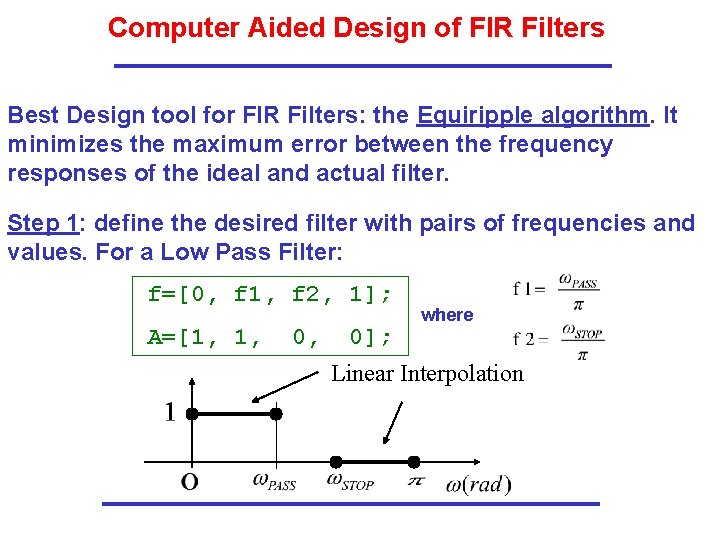
Computer Aided Design of FIR Filters Best Design tool for FIR Filters: the Equiripple algorithm. It minimizes the maximum error between the frequency responses of the ideal and actual filter. Step 1: define the desired filter with pairs of frequencies and values. For a Low Pass Filter: f=[0, f 1, f 2, 1]; A=[1, 1, 0]; where Linear Interpolation

Computer Aided Design of FIR Filters Step 2: Choose filter length N from desired attenuation as Step 3: call “firpm” (pm = Parks, Mc. Clellan) h = firpm(N, f, A); which yields the desired impulse response

Example: Low Pass Filter Passband: 3 k. Hz Stopband: 3. 5 k. Hz Attenuation: 60 d. B Sampling Freq: 15 k. Hz Then compute: h = firpm(82, [0, 2/5, 7/15, 1], [1, 1, 0, 0]);

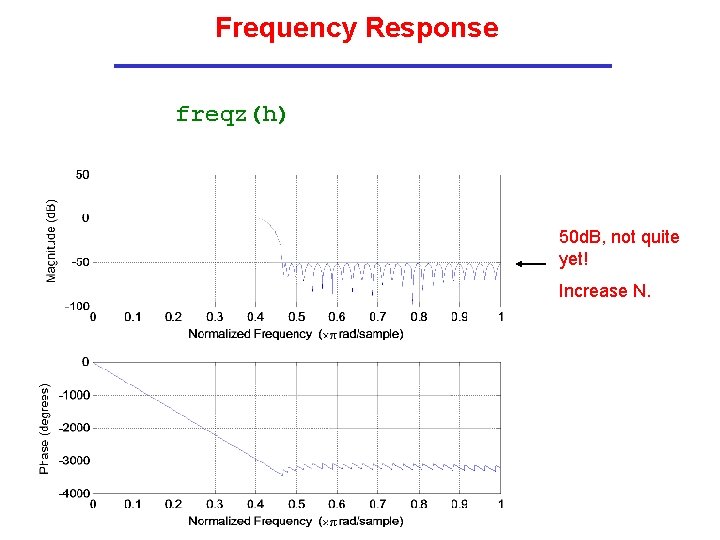
Frequency Response freqz(h) 50 d. B, not quite yet! Increase N.

Increase Filter Length N h=firpm(95, [0, 2/5, 7/15, 1], [1, 1, 0, 0]); freqz(h)

Impulse Response of Example stem(h)

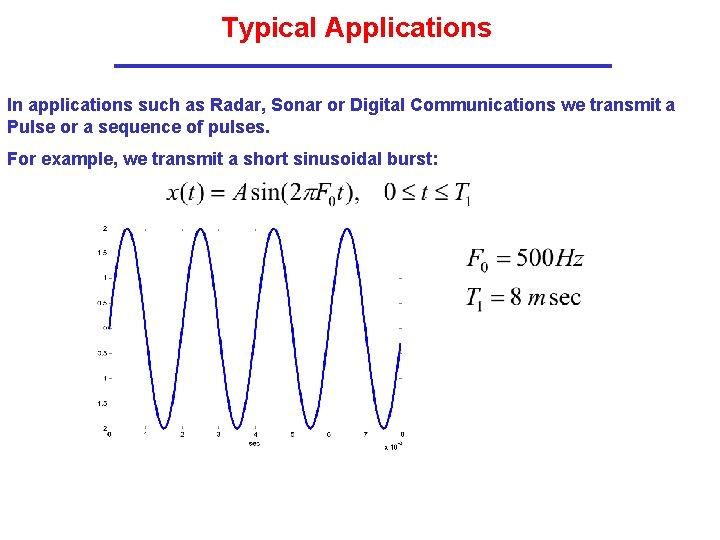
Typical Applications In applications such as Radar, Sonar or Digital Communications we transmit a Pulse or a sequence of pulses. For example, we transmit a short sinusoidal burst:

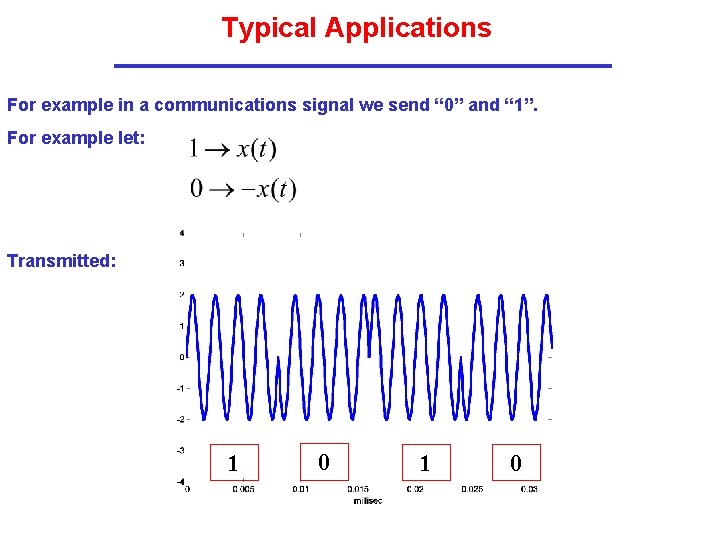
Typical Applications For example in a communications signal we send “ 0” and “ 1”. For example let: Transmitted: 1 0

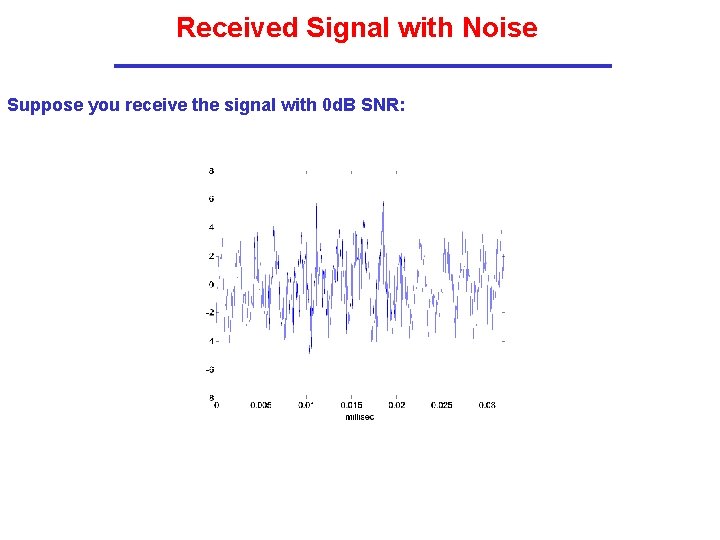
Received Signal with Noise Suppose you receive the signal with 0 d. B SNR:

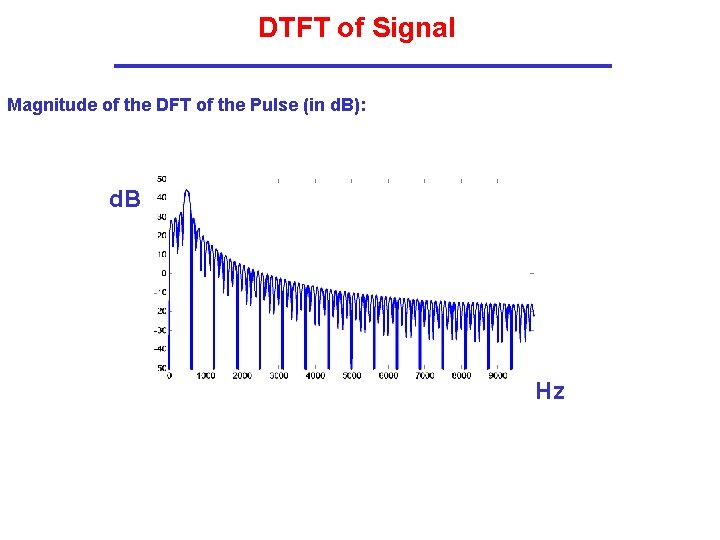
DTFT of Signal Magnitude of the DFT of the Pulse (in d. B): d. B Hz

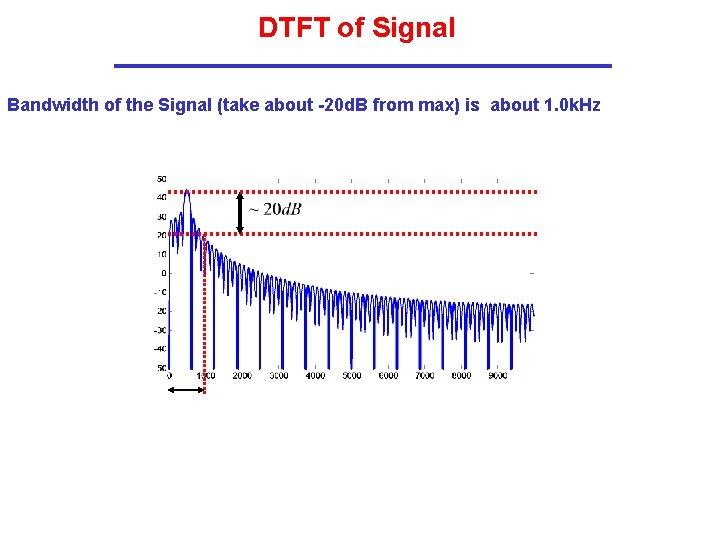
DTFT of Signal Bandwidth of the Signal (take about -20 d. B from max) is about 1. 0 k. Hz

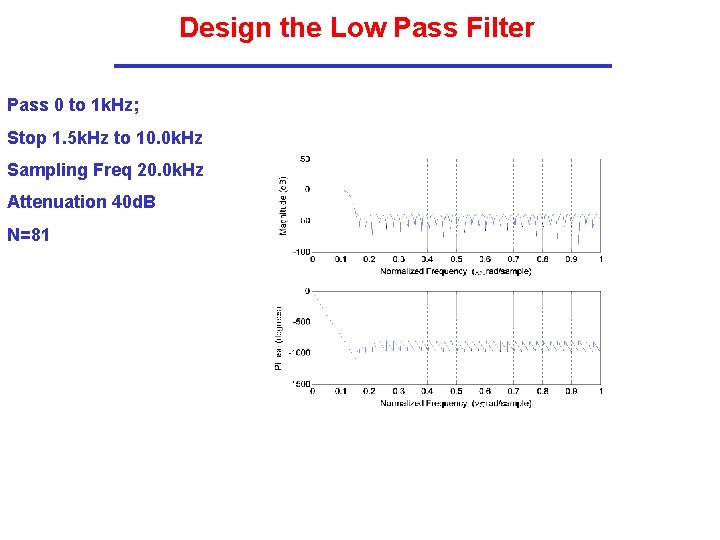
Design the Low Pass Filter Pass 0 to 1 k. Hz; Stop 1. 5 k. Hz to 10. 0 k. Hz Sampling Freq 20. 0 k. Hz Attenuation 40 d. B N=81

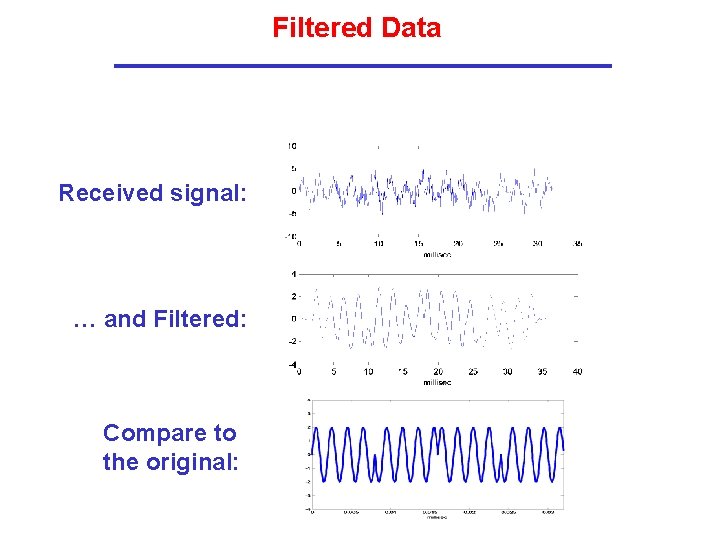
Filtered Data Received signal: … and Filtered: Compare to the original: