Filtering in the Frequency Domain Chapter 4 Chapter

Filtering in the Frequency Domain Chapter 4

Chapter Objectives � This chapter is concerned primarily with establishing a foundation for the Fourier transform and how it is used in basic image filtering. � Fourier Transformation History � The big Idea � Background

History Jean Baptiste Joseph Fourier � Fourier was born in Auxerre, France in 1768 Most famous for his work: � “La. Théorie Analitique de la Chaleur” published in 1822. � � Translated into English in 1878: “The Analytic Theory of Heat” Nobody paid much attention when the work was first published. One of the most important mathematical theories in modern engineering.

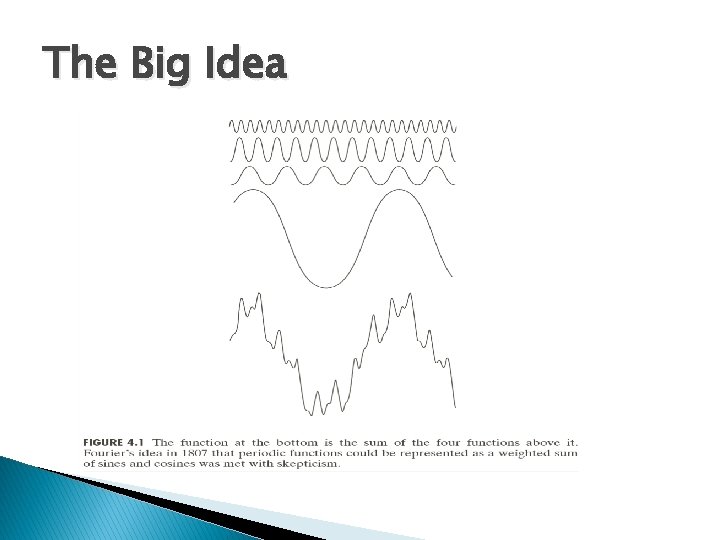
The Big Idea

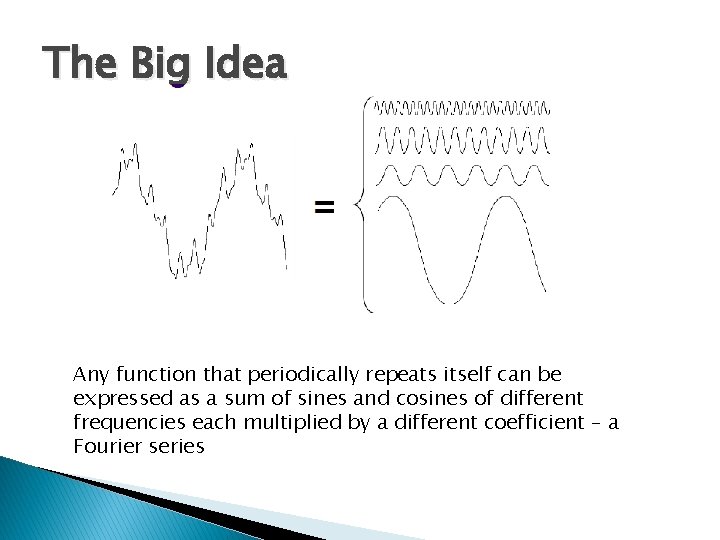
The Big Idea Any function that periodically repeats itself can be expressed as a sum of sines and cosines of different frequencies each multiplied by a different coefficient – a Fourier series

Background � Fourier Series ◦ Any periodically repeated function can be expressed of the sum of sines/cosines of different frequencies, each multiplied by a different coefficient � Fourier Transform ◦ Finite curves can be expressed as the integral of sines/cosines multiplied by a weighing function � wildly used in signal processing field � Fourier Series/Transform can be reconstructed completely via an inverse process with no loss of information

The Frequency Domain � Euler’s formula e jθ = cosθ + j sinθ

Discrete Fourier Transform � 1 D Discrete Fourier Transform � 2 D Discrete Fourier Transform

Basic properties of frequency domain Each term of F(u, v) contains all values of f(x, y) modified by the values of exponential terms � Not easy to make direct association between specific components of an image and its transform � Frequency is related to rate of change ◦ Frequencies in Fourier transform can be associated with patterns of intensity variations in image ◦ Slowest varying frequency component (u = v = 0) corresponds to average gray level of image ◦ As you move away from origin of transform, low frequencies correspond to slowly varying components of image ◦ Farther away from origin, you have higher frequencies corresponding to faster gray level changes �

Filtering Images in the Frequency Domain

Filtering Images in the Frequency Domain

Filtering Images in the Frequency Domain � Filter or filter transfer function ◦ Suppresses certain frequencies in transform while leaving others unchanged � Fourier transform of the output image G(u, v) = H(u, v) · F(u, v) � Multiplication of H and F is only between corresponding elements G(0, 0) = H(0, 0) · F(0, 0)

Filtering Scheme

Filters in the Frequency Domain � Image Smoothing Using Frequency Domain Filters: � Image sharpening Using Frequency Domain Filters: ◦ Ideal Lowpass Filters ◦ Butterworth Lowpass Filters ◦ Gaussian Lowpass Filters. ◦ ◦ ◦ Ideal Highpass Filters Butterworth Highpass Filters Gaussian Highpass Filters. The Laplacian in the Frequency Domain Unsharp Masking, Highboost Filtering, and High-Frequency -Emphasis Filtering