FIGURES FOR CHAPTER 12 REVIEW OF CENTROIDS AND

FIGURES FOR CHAPTER 12 REVIEW OF CENTROIDS AND MOMENTS OF INERTIA Click the mouse or use the arrow keys to move to the next page. Use the ESC key to exit this chapter. Copyright 2005 by Nelson, a division of Thomson Canada Limited

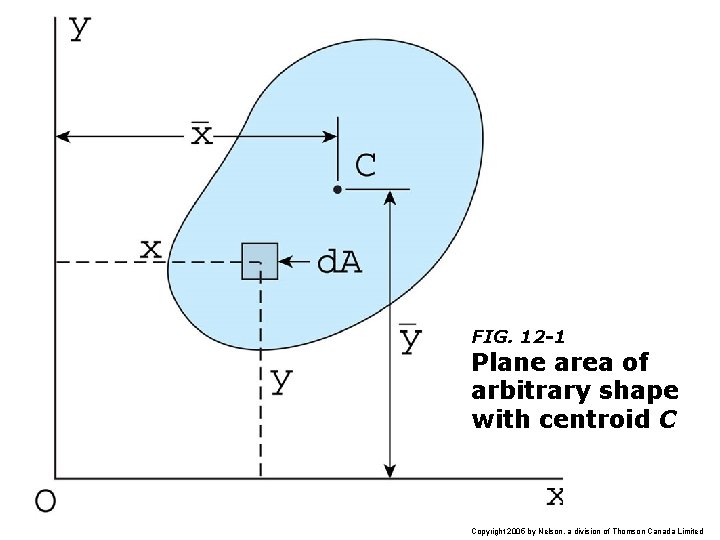
FIG. 12 -1 Plane area of arbitrary shape with centroid C Copyright 2005 by Nelson, a division of Thomson Canada Limited

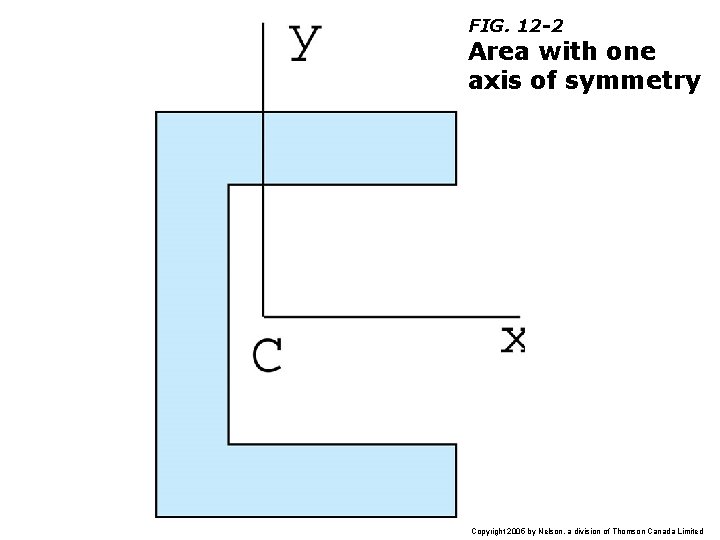
FIG. 12 -2 Area with one axis of symmetry Copyright 2005 by Nelson, a division of Thomson Canada Limited

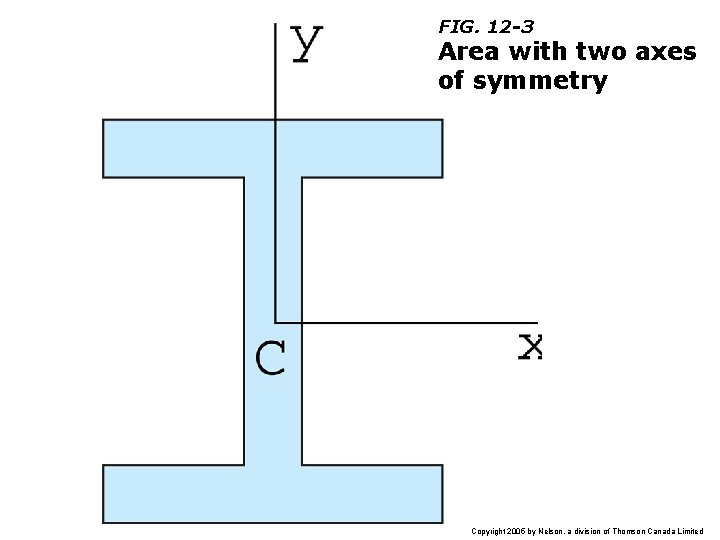
FIG. 12 -3 Area with two axes of symmetry Copyright 2005 by Nelson, a division of Thomson Canada Limited

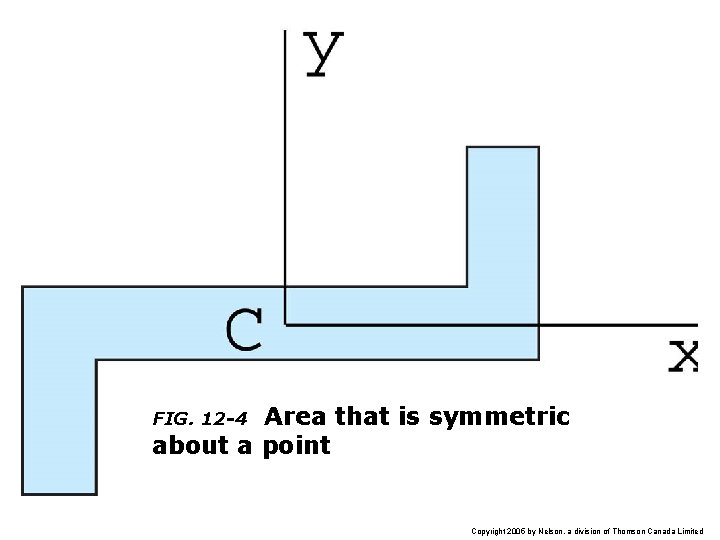
Area that is symmetric about a point FIG. 12 -4 Copyright 2005 by Nelson, a division of Thomson Canada Limited

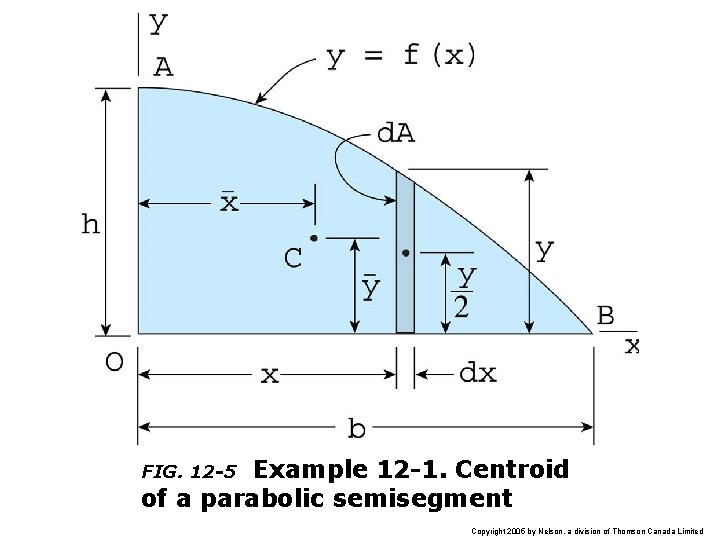
Example 12 -1. Centroid of a parabolic semisegment FIG. 12 -5 Copyright 2005 by Nelson, a division of Thomson Canada Limited

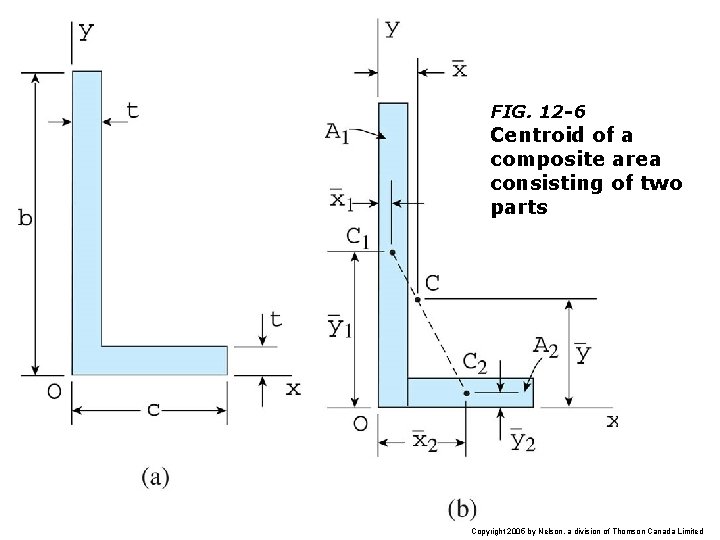
FIG. 12 -6 Centroid of a composite area consisting of two parts Copyright 2005 by Nelson, a division of Thomson Canada Limited

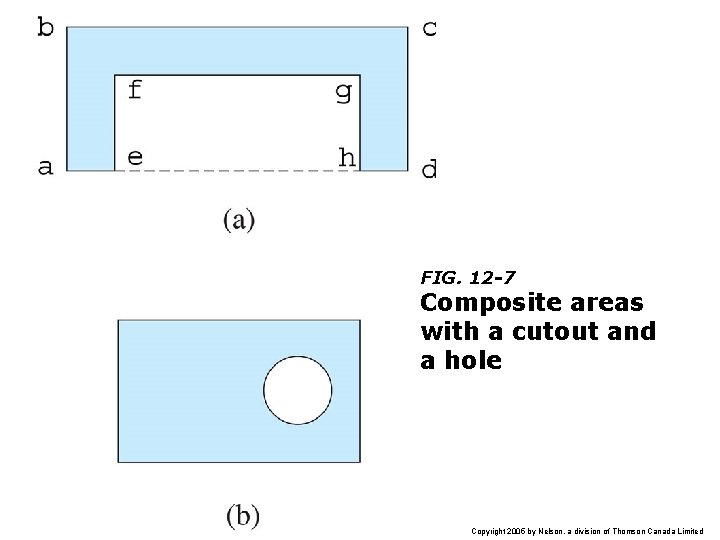
FIG. 12 -7 Composite areas with a cutout and a hole Copyright 2005 by Nelson, a division of Thomson Canada Limited

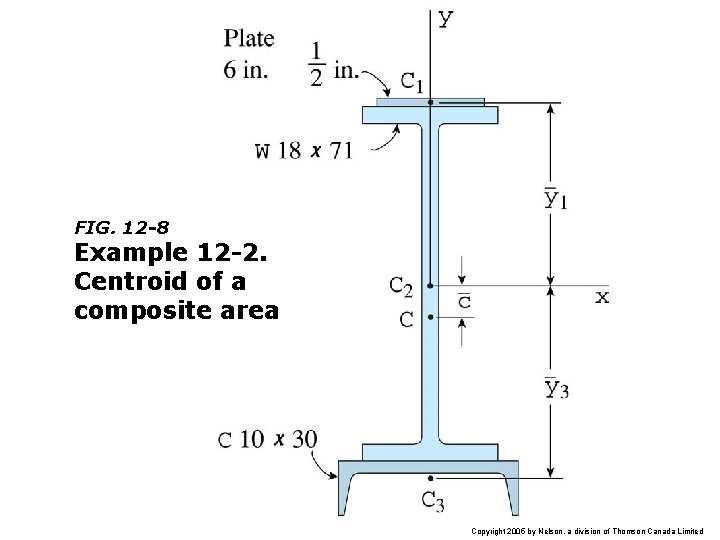
FIG. 12 -8 Example 12 -2. Centroid of a composite area Copyright 2005 by Nelson, a division of Thomson Canada Limited

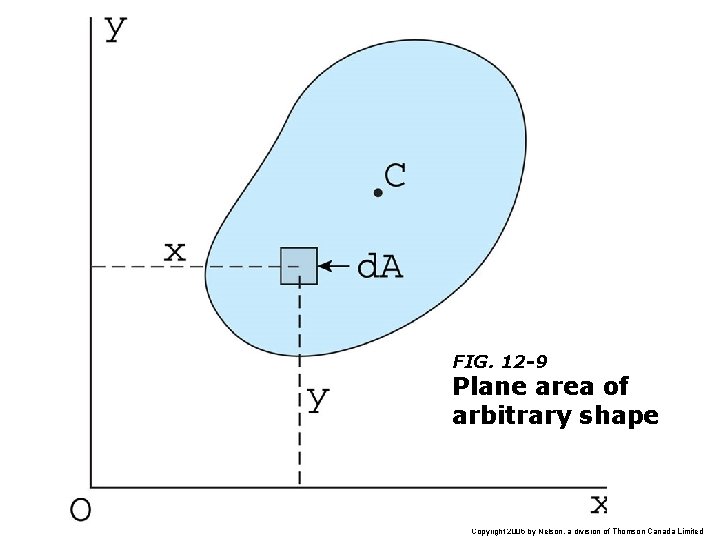
FIG. 12 -9 Plane area of arbitrary shape Copyright 2005 by Nelson, a division of Thomson Canada Limited

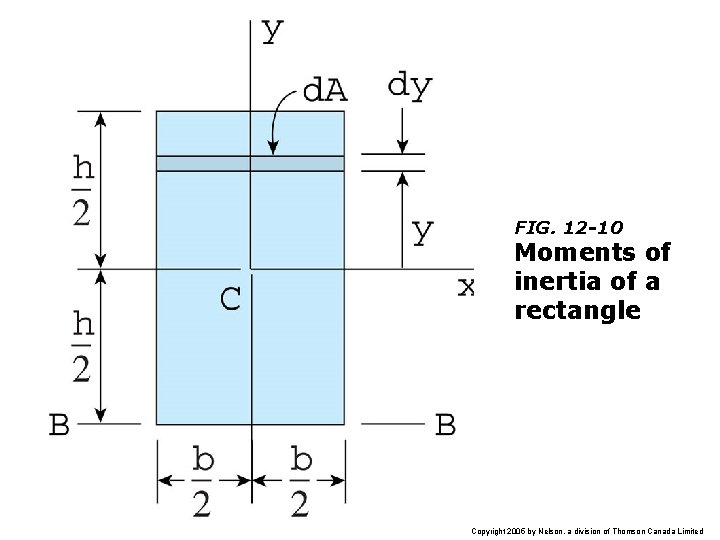
FIG. 12 -10 Moments of inertia of a rectangle Copyright 2005 by Nelson, a division of Thomson Canada Limited

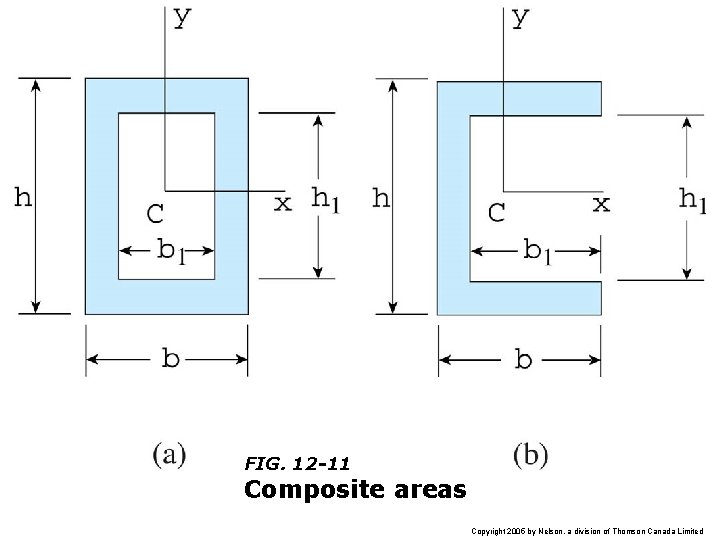
FIG. 12 -11 Composite areas Copyright 2005 by Nelson, a division of Thomson Canada Limited

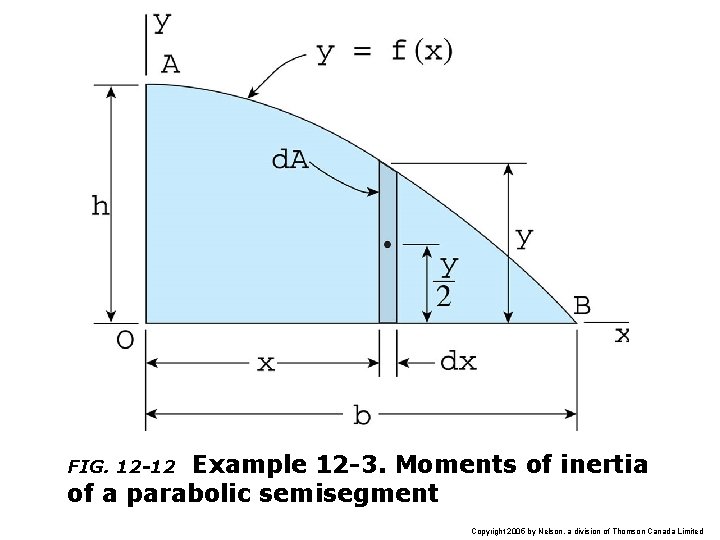
Example 12 -3. Moments of inertia of a parabolic semisegment FIG. 12 -12 Copyright 2005 by Nelson, a division of Thomson Canada Limited

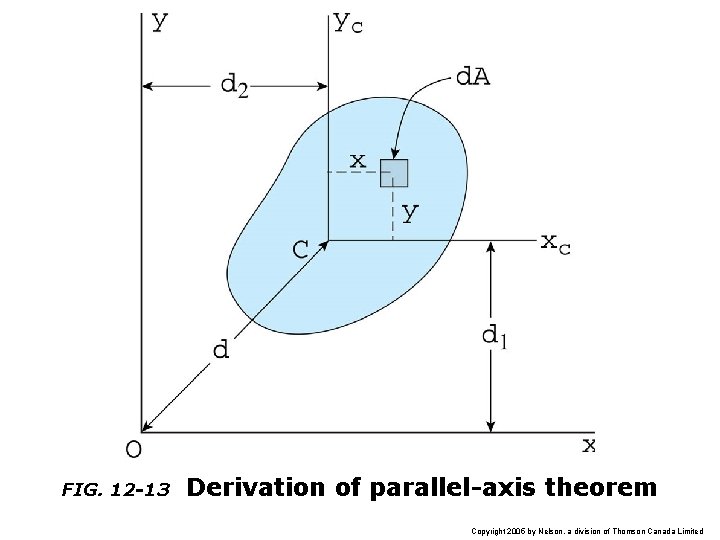
FIG. 12 -13 Derivation of parallel-axis theorem Copyright 2005 by Nelson, a division of Thomson Canada Limited

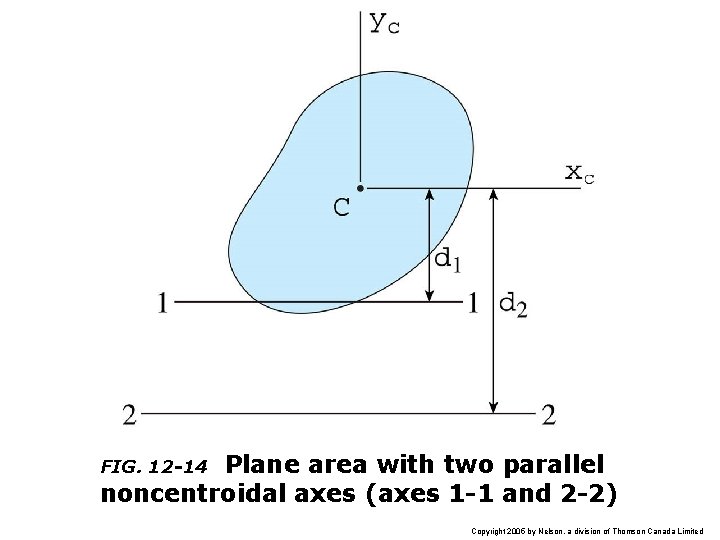
Plane area with two parallel noncentroidal axes (axes 1 -1 and 2 -2) FIG. 12 -14 Copyright 2005 by Nelson, a division of Thomson Canada Limited

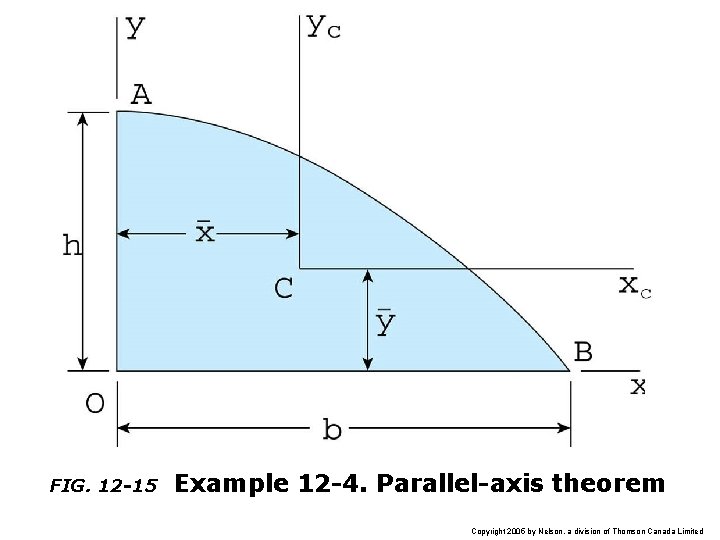
FIG. 12 -15 Example 12 -4. Parallel-axis theorem Copyright 2005 by Nelson, a division of Thomson Canada Limited

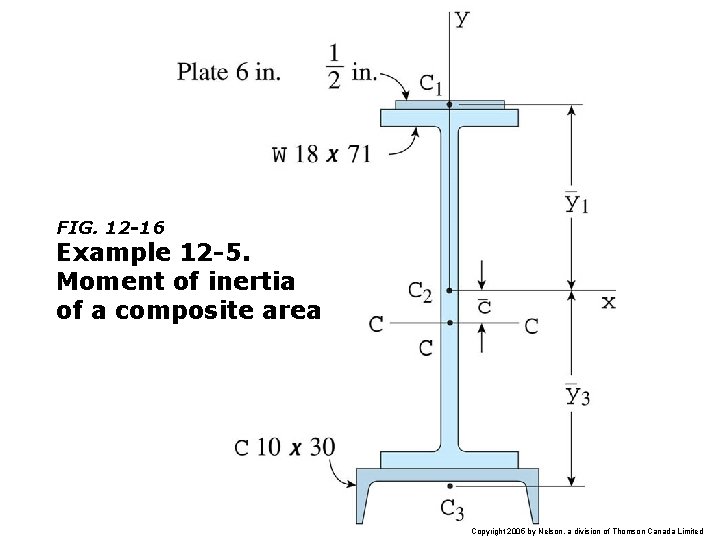
FIG. 12 -16 Example 12 -5. Moment of inertia of a composite area Copyright 2005 by Nelson, a division of Thomson Canada Limited

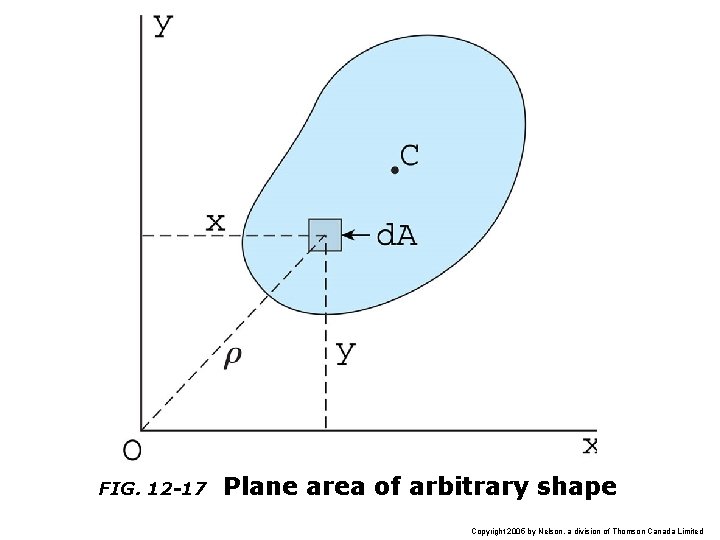
FIG. 12 -17 Plane area of arbitrary shape Copyright 2005 by Nelson, a division of Thomson Canada Limited

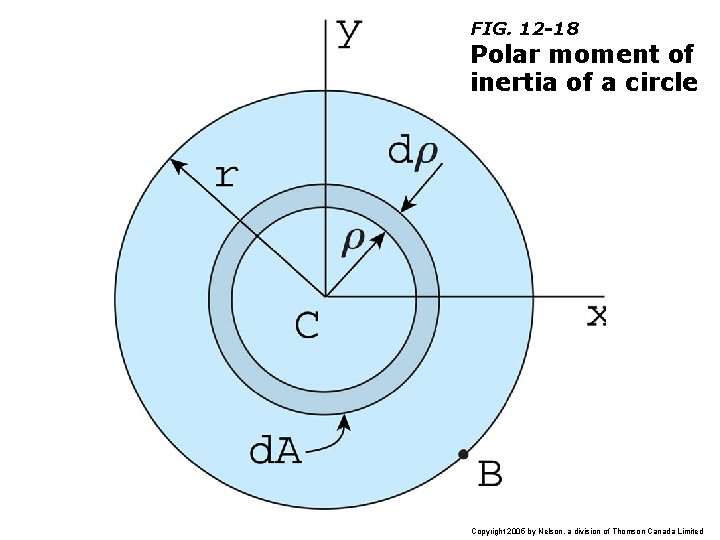
FIG. 12 -18 Polar moment of inertia of a circle Copyright 2005 by Nelson, a division of Thomson Canada Limited

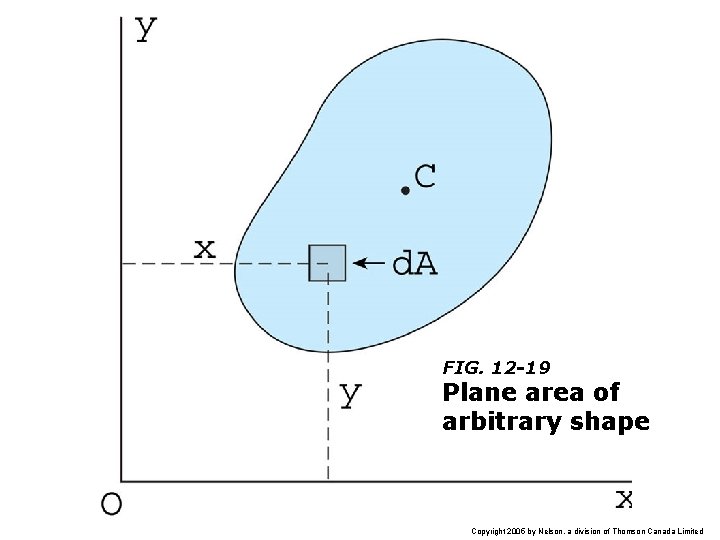
FIG. 12 -19 Plane area of arbitrary shape Copyright 2005 by Nelson, a division of Thomson Canada Limited

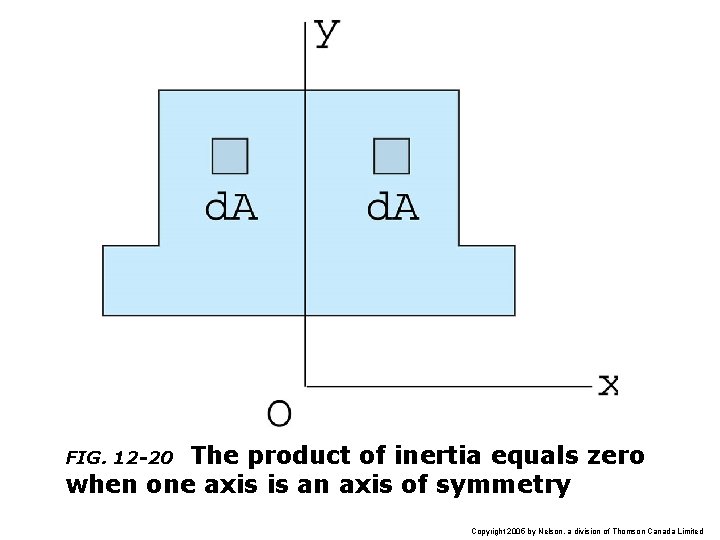
The product of inertia equals zero when one axis is an axis of symmetry FIG. 12 -20 Copyright 2005 by Nelson, a division of Thomson Canada Limited

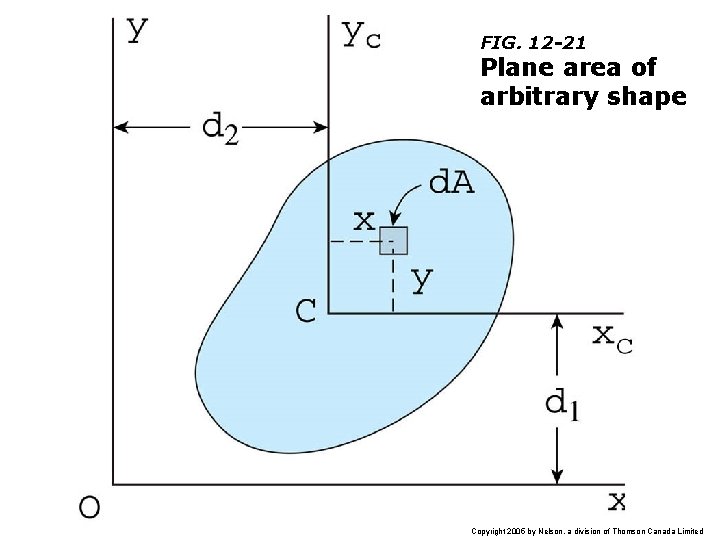
FIG. 12 -21 Plane area of arbitrary shape Copyright 2005 by Nelson, a division of Thomson Canada Limited

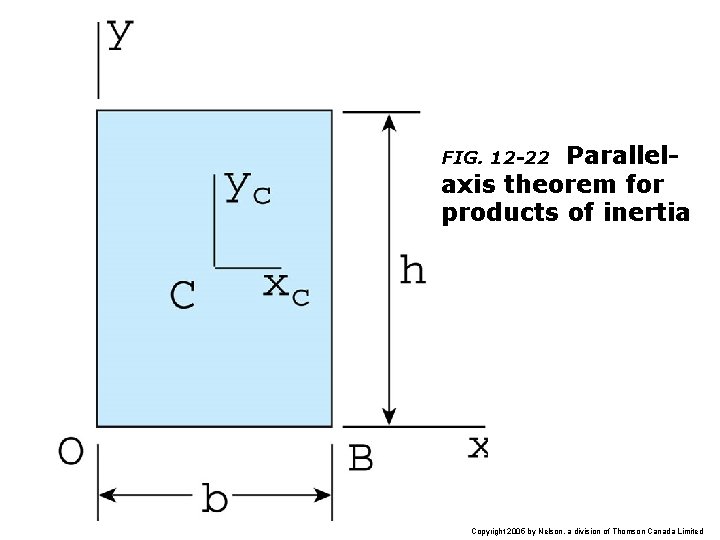
Parallelaxis theorem for products of inertia FIG. 12 -22 Copyright 2005 by Nelson, a division of Thomson Canada Limited

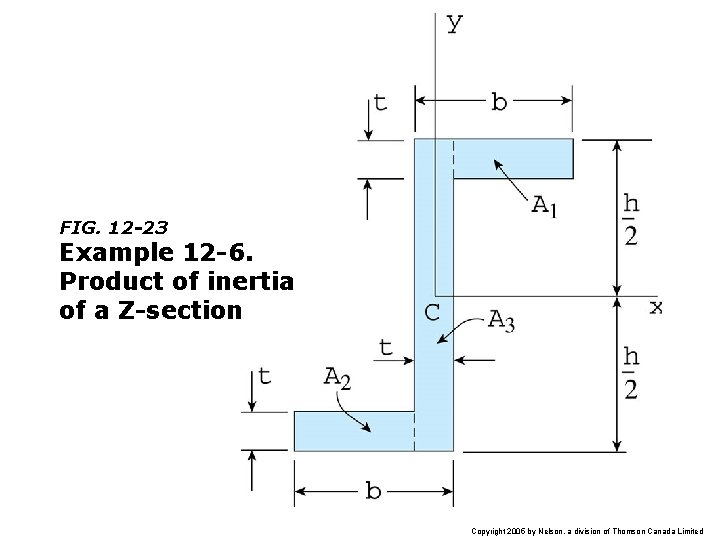
FIG. 12 -23 Example 12 -6. Product of inertia of a Z-section Copyright 2005 by Nelson, a division of Thomson Canada Limited

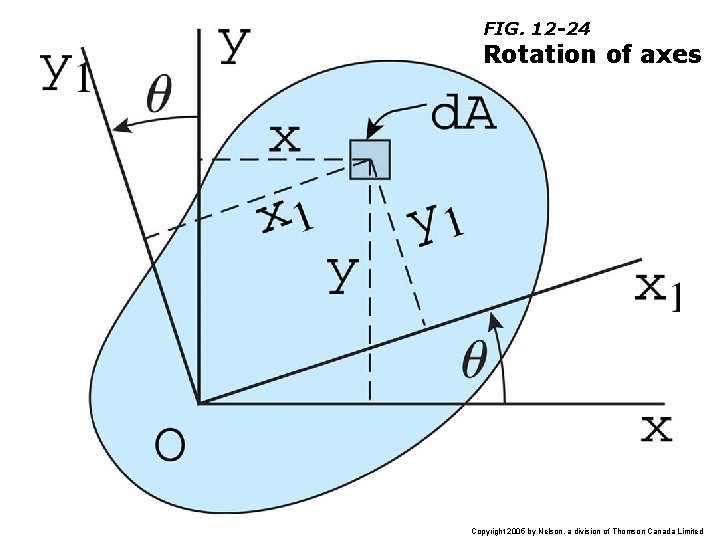
FIG. 12 -24 Rotation of axes Copyright 2005 by Nelson, a division of Thomson Canada Limited

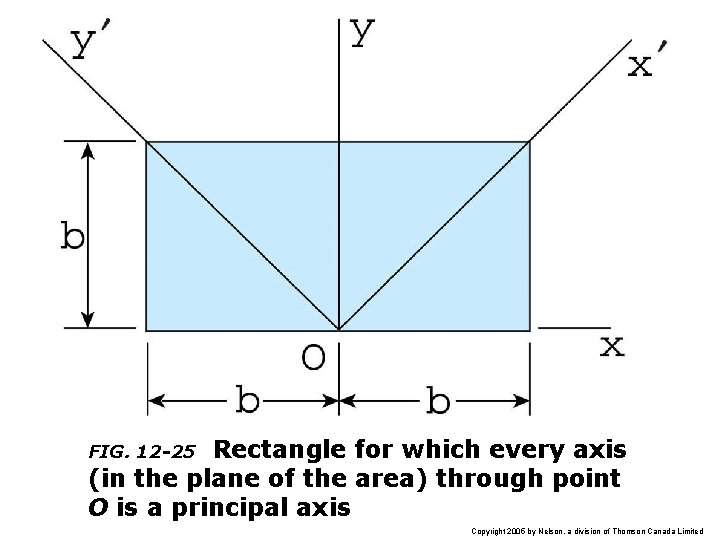
Rectangle for which every axis (in the plane of the area) through point O is a principal axis FIG. 12 -25 Copyright 2005 by Nelson, a division of Thomson Canada Limited

FIG. 12 -26 Examples of areas for which every centroidal axis is a principal axis and the centroid C is a principal point Copyright 2005 by Nelson, a division of Thomson Canada Limited

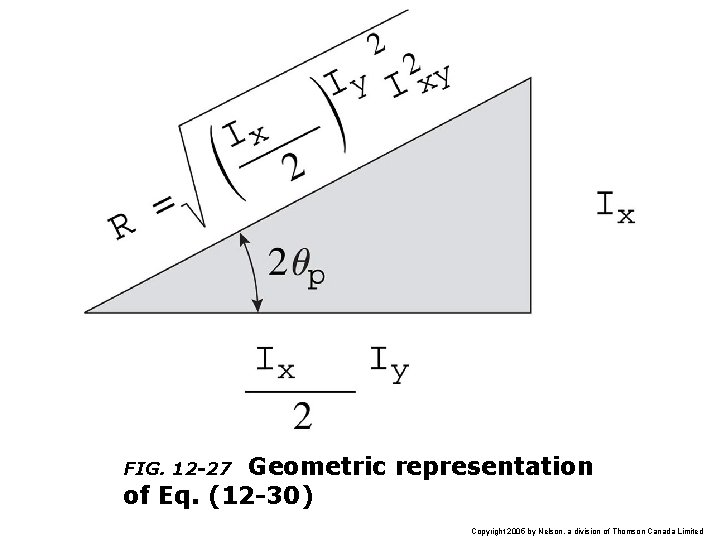
Geometric representation of Eq. (12 -30) FIG. 12 -27 Copyright 2005 by Nelson, a division of Thomson Canada Limited

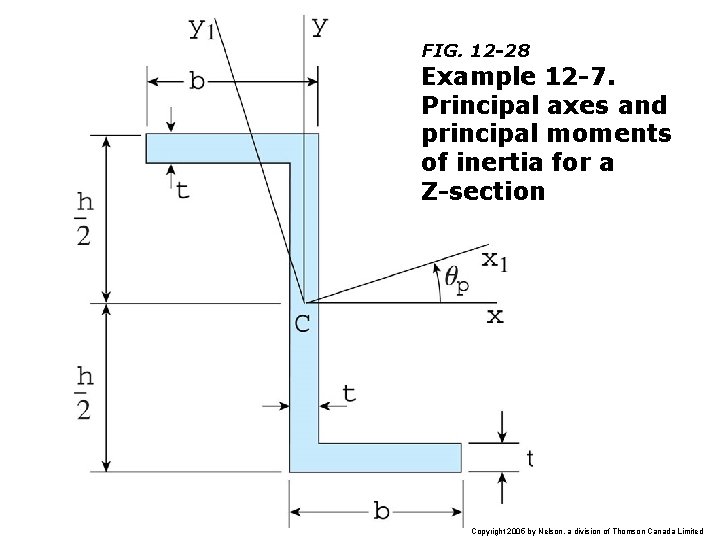
FIG. 12 -28 Example 12 -7. Principal axes and principal moments of inertia for a Z-section Copyright 2005 by Nelson, a division of Thomson Canada Limited

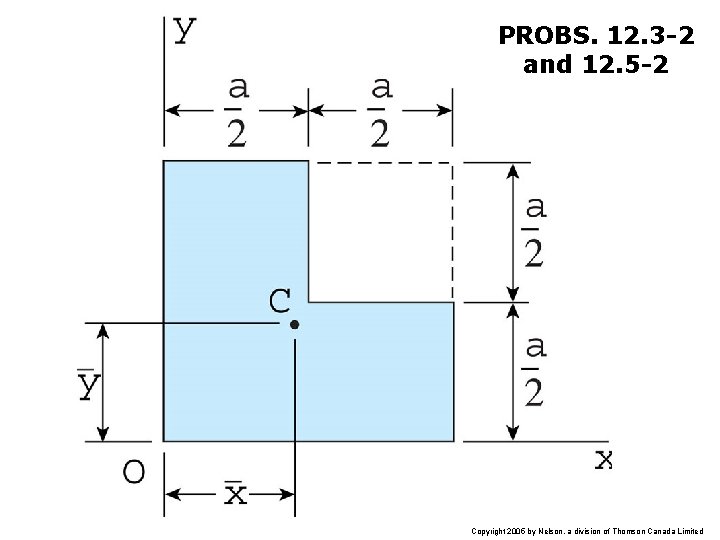
PROBS. 12. 3 -2 and 12. 5 -2 Copyright 2005 by Nelson, a division of Thomson Canada Limited

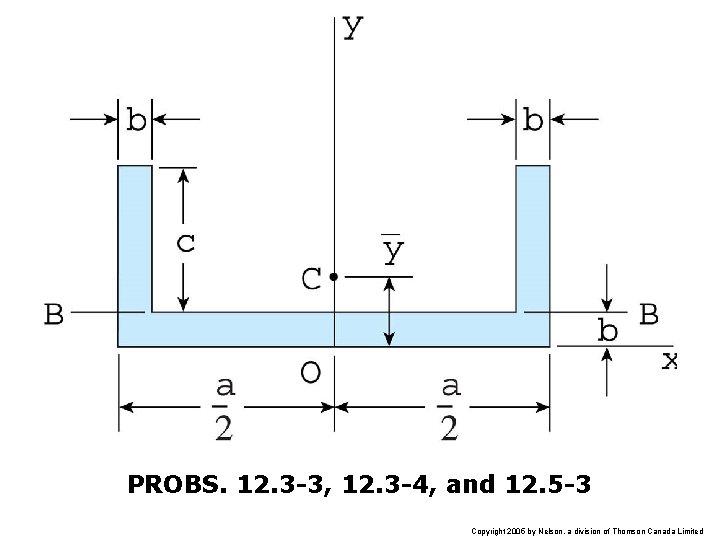
PROBS. 12. 3 -3, 12. 3 -4, and 12. 5 -3 Copyright 2005 by Nelson, a division of Thomson Canada Limited

PROBS. 12. 3 -5 and 12. 5 -5 Copyright 2005 by Nelson, a division of Thomson Canada Limited

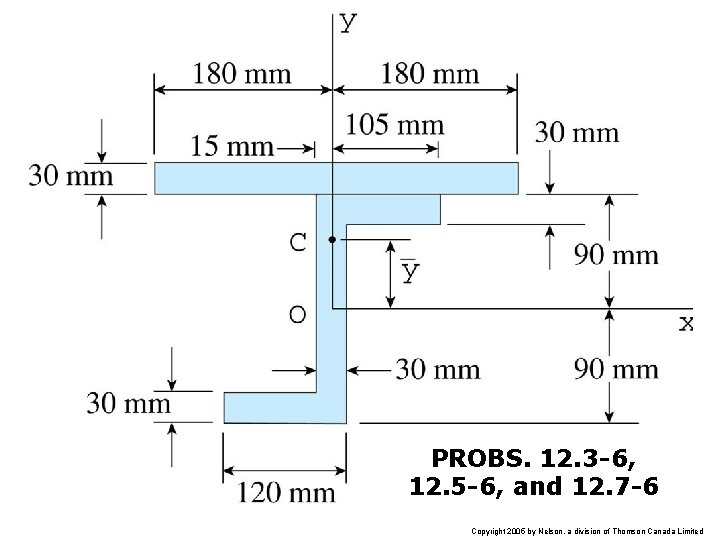
PROBS. 12. 3 -6, 12. 5 -6, and 12. 7 -6 Copyright 2005 by Nelson, a division of Thomson Canada Limited

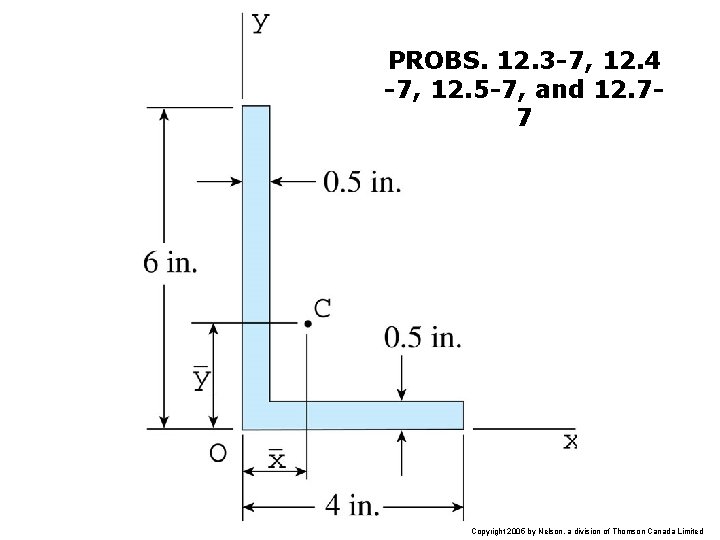
PROBS. 12. 3 -7, 12. 4 -7, 12. 5 -7, and 12. 77 Copyright 2005 by Nelson, a division of Thomson Canada Limited

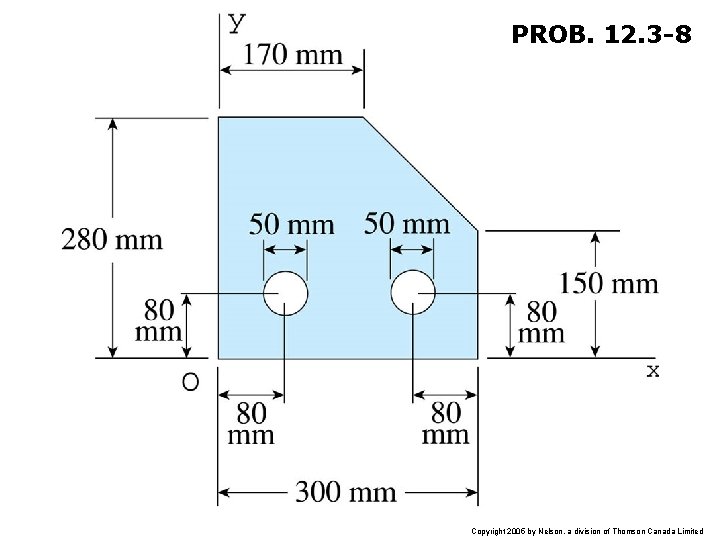
PROB. 12. 3 -8 Copyright 2005 by Nelson, a division of Thomson Canada Limited

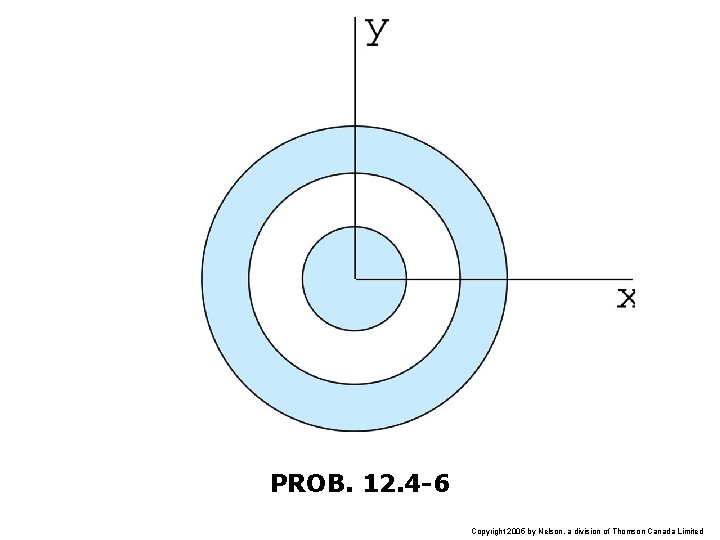
PROB. 12. 4 -6 Copyright 2005 by Nelson, a division of Thomson Canada Limited

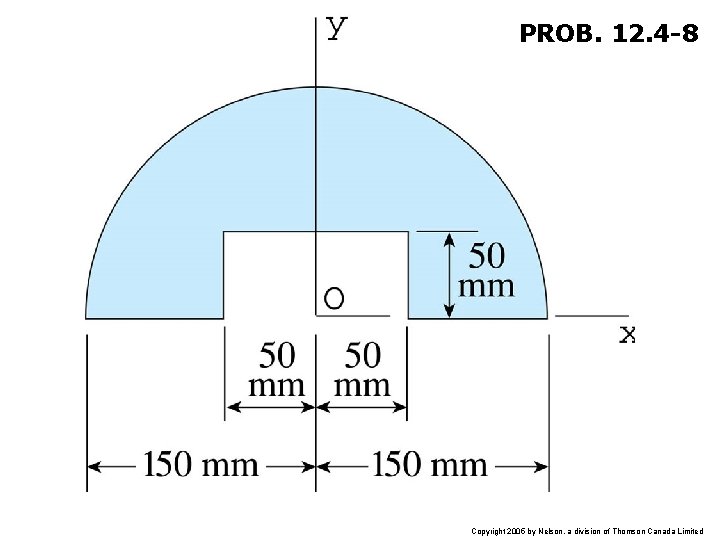
PROB. 12. 4 -8 Copyright 2005 by Nelson, a division of Thomson Canada Limited

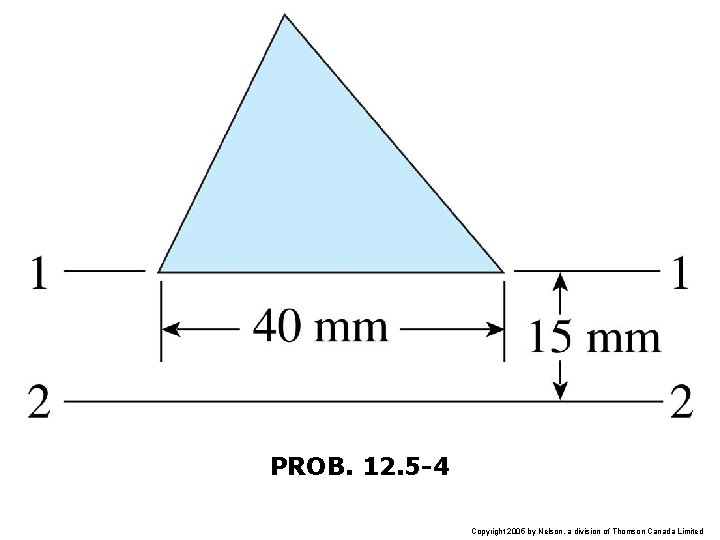
PROB. 12. 5 -4 Copyright 2005 by Nelson, a division of Thomson Canada Limited

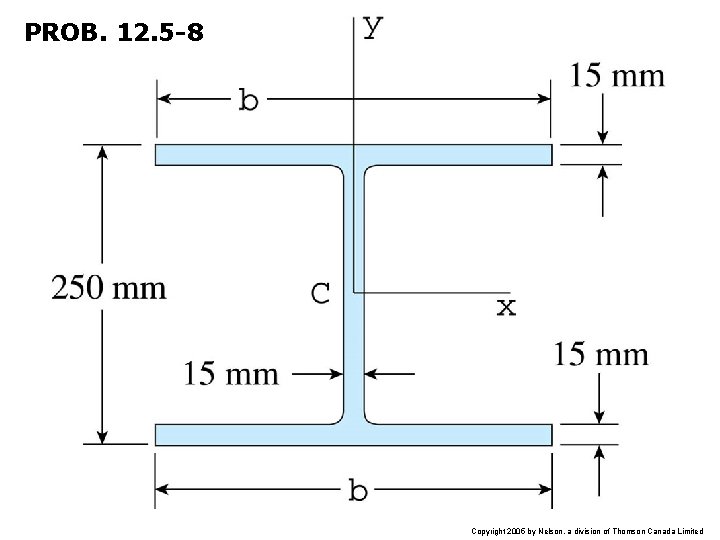
PROB. 12. 5 -8 Copyright 2005 by Nelson, a division of Thomson Canada Limited

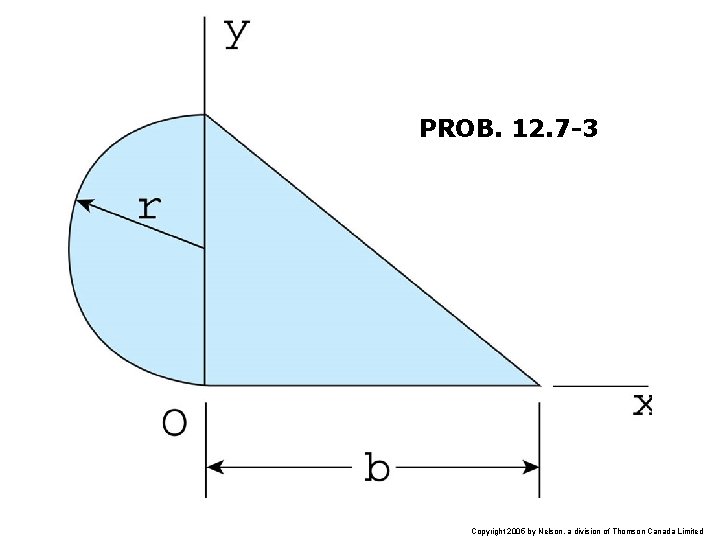
PROB. 12. 7 -3 Copyright 2005 by Nelson, a division of Thomson Canada Limited

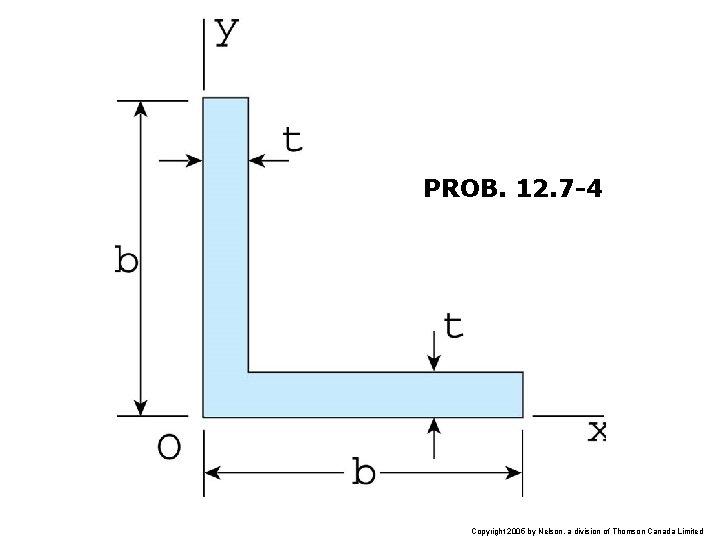
PROB. 12. 7 -4 Copyright 2005 by Nelson, a division of Thomson Canada Limited

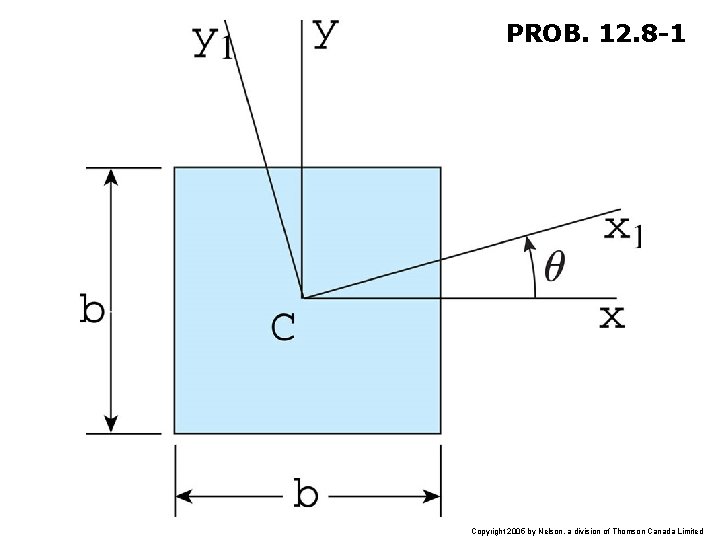
PROB. 12. 8 -1 Copyright 2005 by Nelson, a division of Thomson Canada Limited

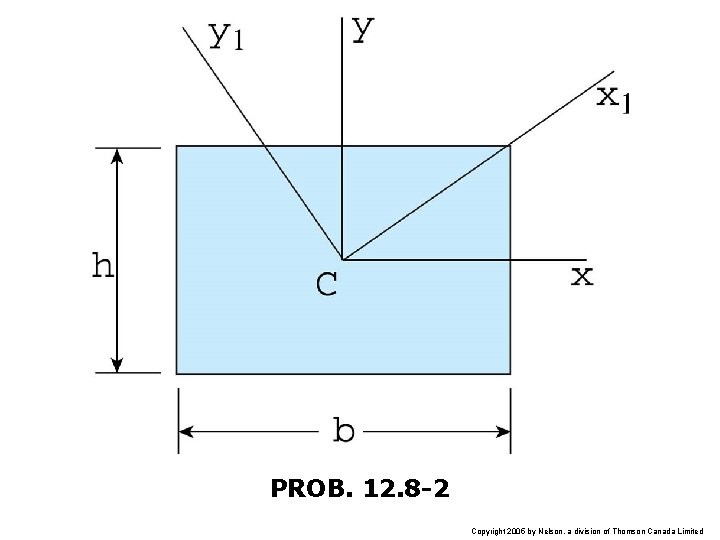
PROB. 12. 8 -2 Copyright 2005 by Nelson, a division of Thomson Canada Limited

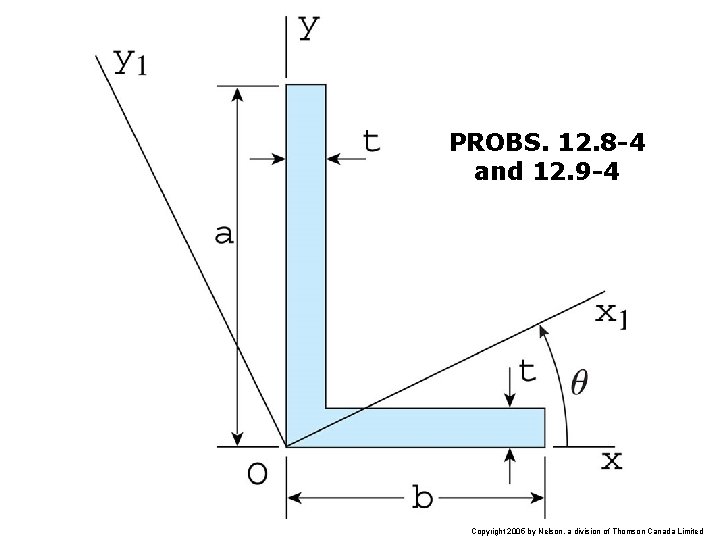
PROBS. 12. 8 -4 and 12. 9 -4 Copyright 2005 by Nelson, a division of Thomson Canada Limited

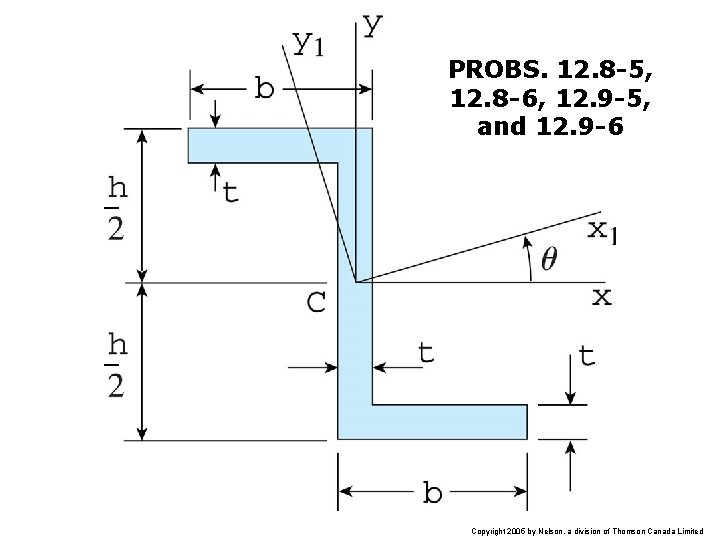
PROBS. 12. 8 -5, 12. 8 -6, 12. 9 -5, and 12. 9 -6 Copyright 2005 by Nelson, a division of Thomson Canada Limited

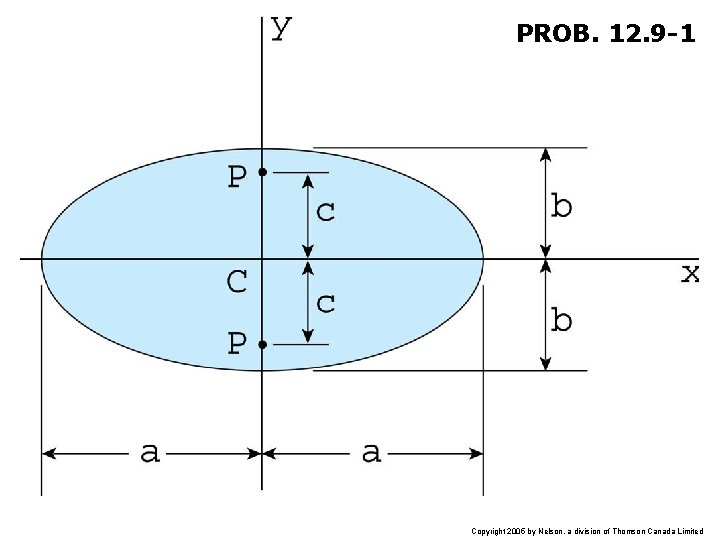
PROB. 12. 9 -1 Copyright 2005 by Nelson, a division of Thomson Canada Limited

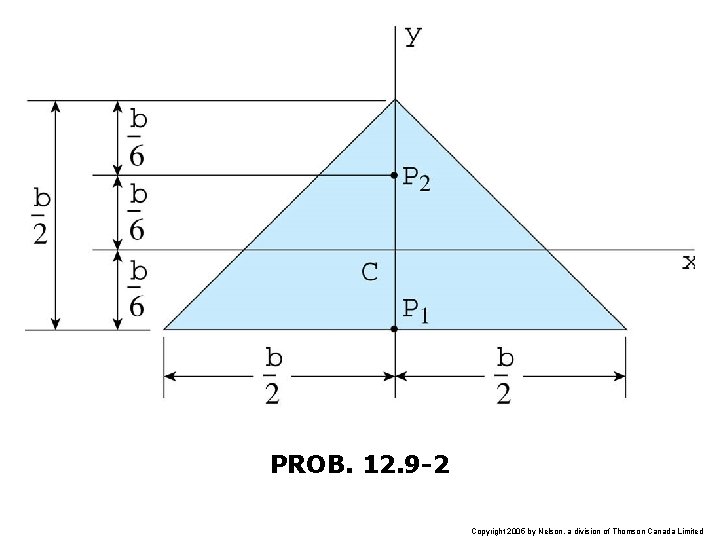
PROB. 12. 9 -2 Copyright 2005 by Nelson, a division of Thomson Canada Limited

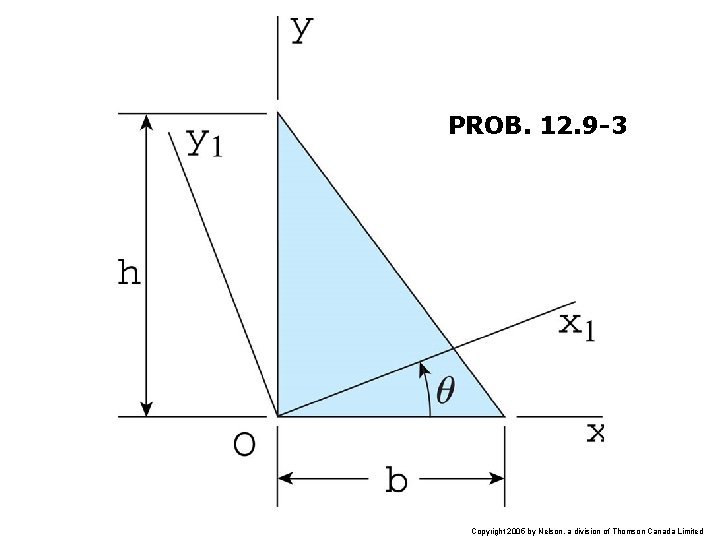
PROB. 12. 9 -3 Copyright 2005 by Nelson, a division of Thomson Canada Limited

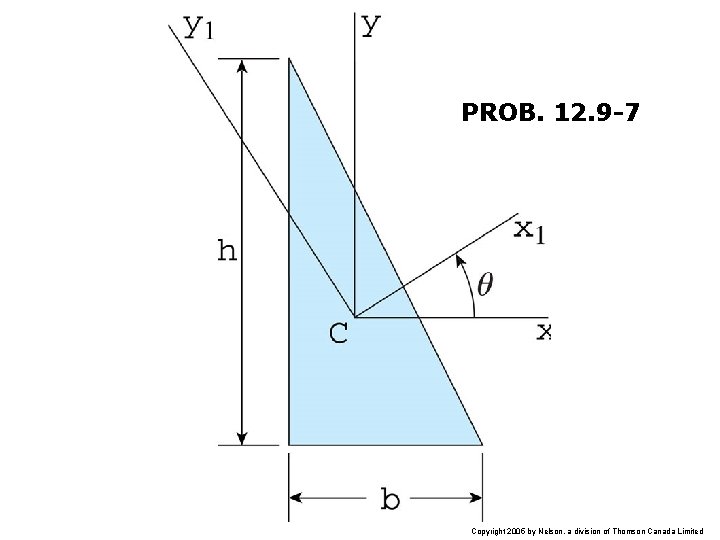
PROB. 12. 9 -7 Copyright 2005 by Nelson, a division of Thomson Canada Limited

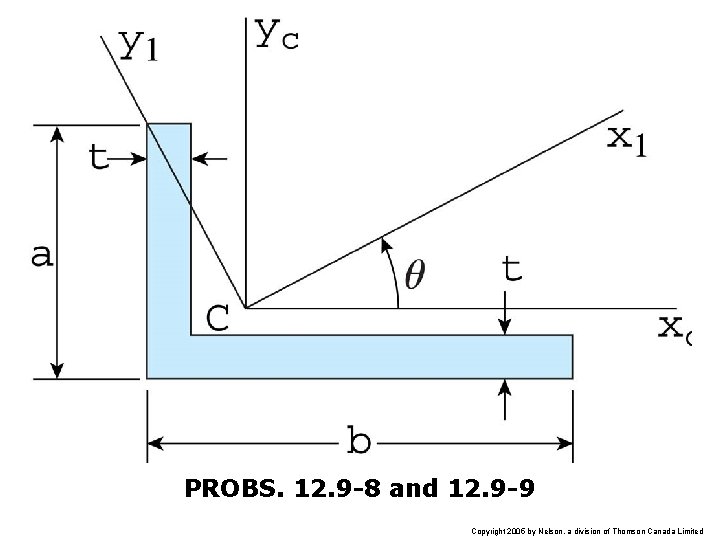
PROBS. 12. 9 -8 and 12. 9 -9 Copyright 2005 by Nelson, a division of Thomson Canada Limited