Figure 5 1 Conversion from decimal to binary

Figure 5. 1. Conversion from decimal to binary.

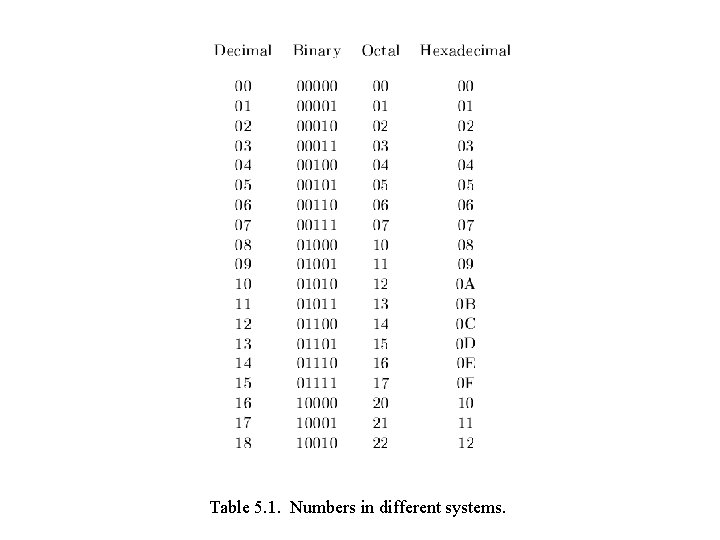
Table 5. 1. Numbers in different systems.

Please see “portrait orientation” Power. Point file for Chapter 5 Figure 5. 2. Half-adder.

Figure 5. 3. An example of addition.

Please see “portrait orientation” Power. Point file for Chapter 5 Figure 5. 4. Full-adder.

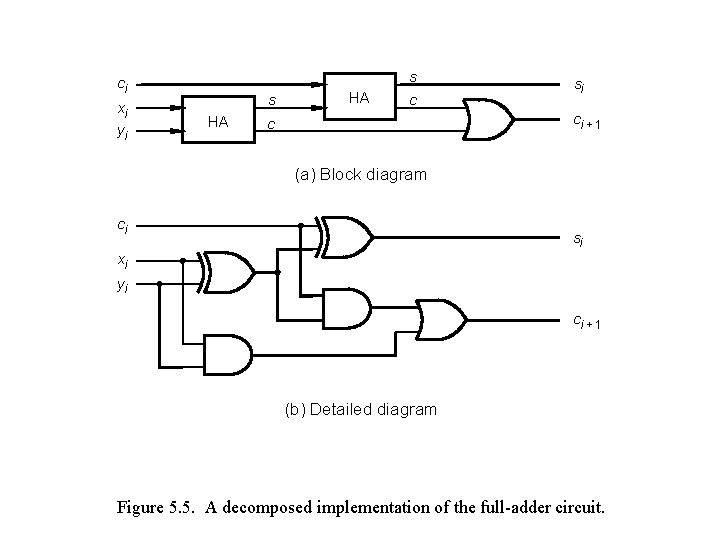
s ci xi yi s HA HA c si ci + 1 c (a) Block diagram ci si xi yi ci + 1 (b) Detailed diagram Figure 5. 5. A decomposed implementation of the full-adder circuit.

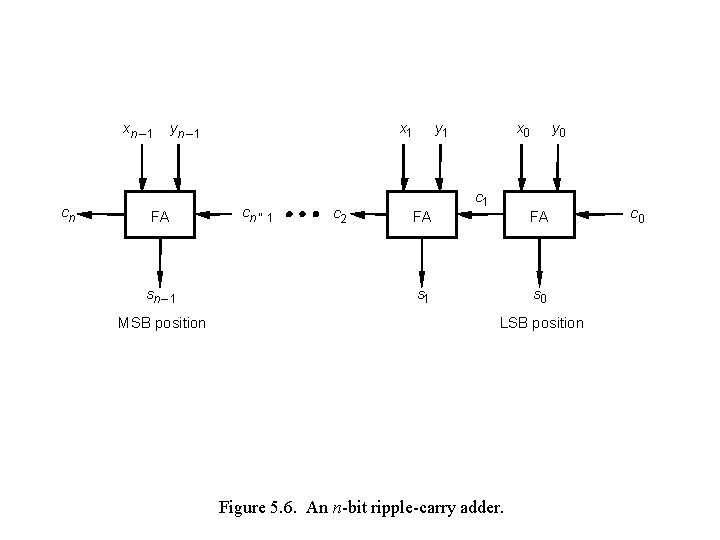
xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn ” 1 c 2 y 1 FA x 0 c 1 y 0 FA s 1 s 0 LSB position Figure 5. 6. An n-bit ripple-carry adder. c 0

Please see “portrait orientation” Power. Point file for Chapter 5 Figure 5. 7. Circuit that multiplies an 8 -bit unsigned number by 3.

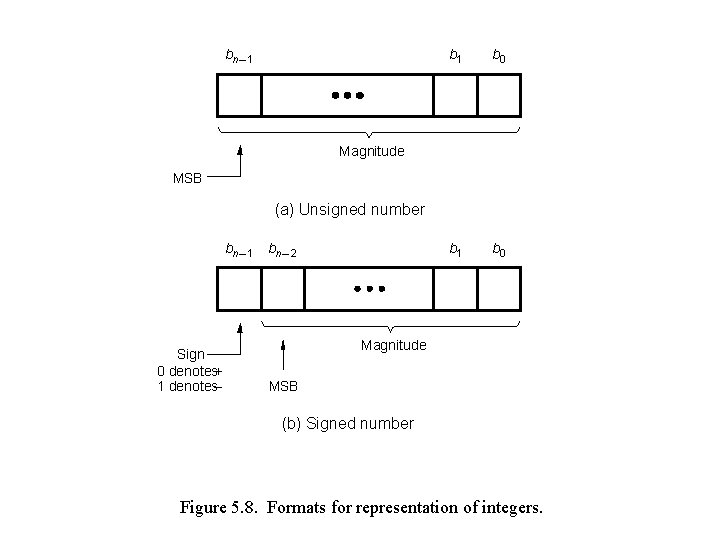
bn – 1 b 0 b 1 b 0 Magnitude MSB (a) Unsigned number bn – 1 bn – 2 Sign 0 denotes+ 1 denotes– Magnitude MSB (b) Signed number Figure 5. 8. Formats for representation of integers.

Table 5. 2. Interpretation of four-bit signed integers.

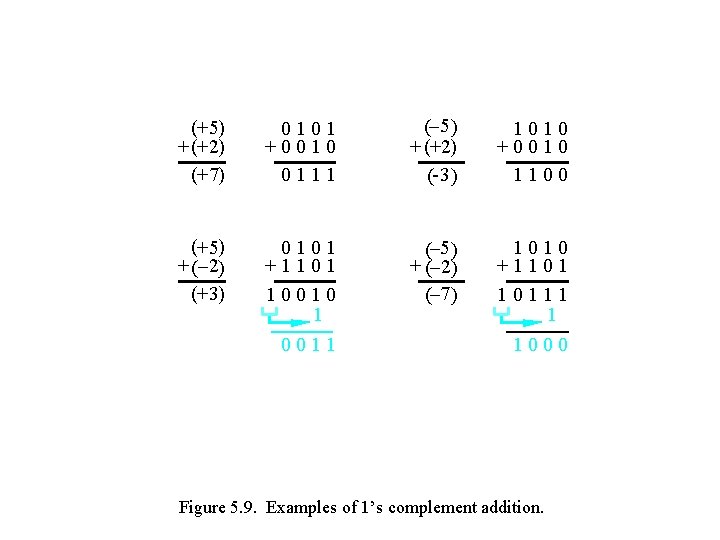
(+ 5) + (+ 2) (+ 7) 0 1 + 0 0 1 1 1 (– 5 ) + (+ 2) (- 3 ) 1 0 + 0 0 1 1 0 0 (+ 5) + (– 2) (+ 3) 0 1 + 1 1 0 0 1 1 (– 5 ) + (– 2 ) (– 7 ) 1 0 + 1 1 0 1 1 1 0 0 0 Figure 5. 9. Examples of 1’s complement addition.

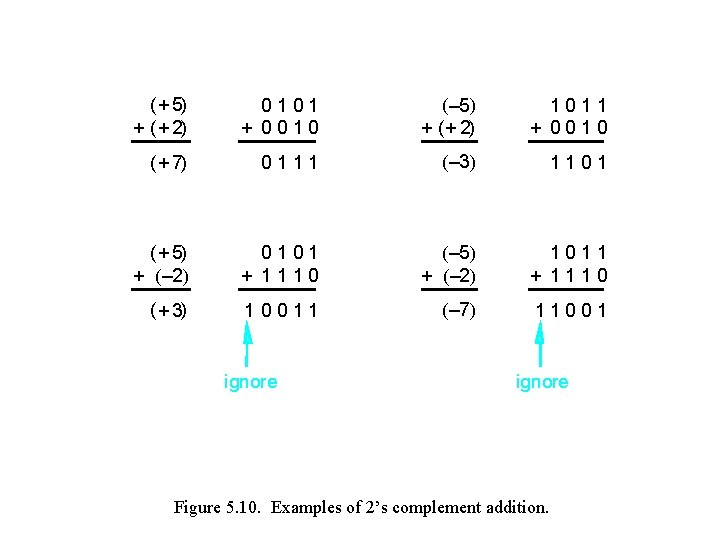
( + 5) + ( + 2) 0101 + 0010 (– 5) + ( + 2) 1011 + 0010 ( + 7) 0111 (– 3) 1101 ( + 5) + (– 2) 0101 + 1110 (– 5) + (– 2) 1011 + 1110 ( + 3) 10011 (– 7) 11 0 0 1 ignore Figure 5. 10. Examples of 2’s complement addition.

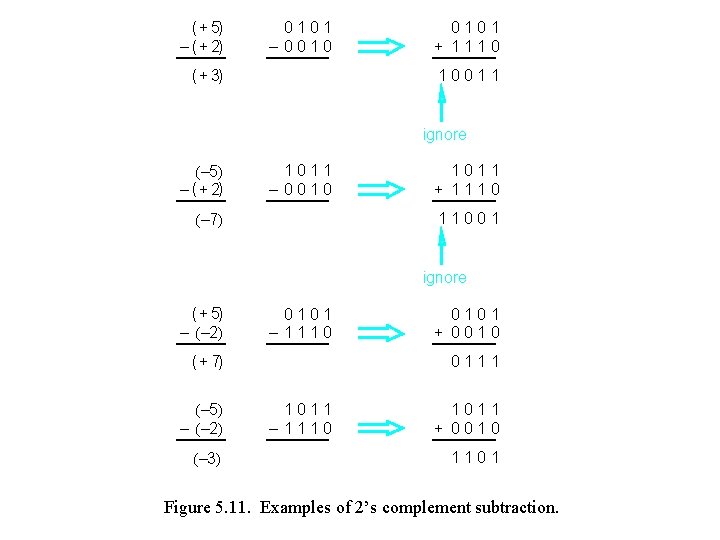
( + 5) – ( + 2) 0101 – 0010 ( + 3) 0101 + 1110 10011 ignore (– 5) – ( + 2) 1011 – 0010 (– 7) 1011 + 1110 11001 ignore ( + 5) – (– 2) 0101 – 1110 ( + 7) (– 5) – (– 2) (– 3) 0101 + 0010 0111 1011 – 1110 1011 + 0010 1101 Figure 5. 11. Examples of 2’s complement subtraction.

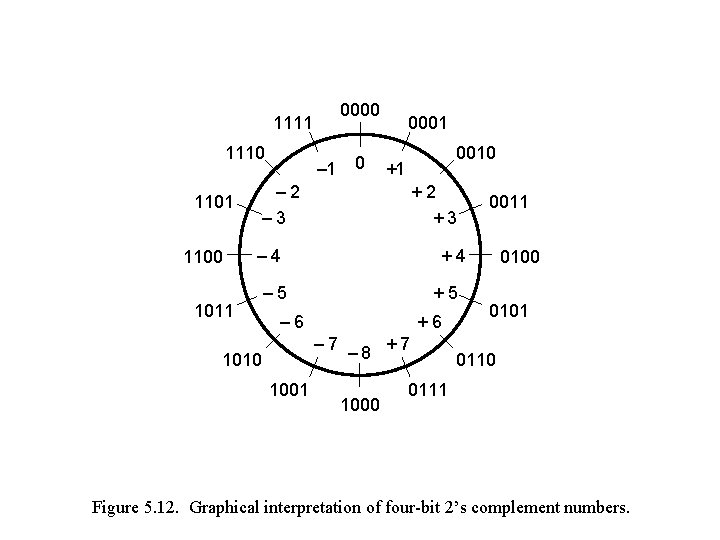
0000 1111 1110 1101 1100 – 1 0 0001 0010 +1 – 2 – 3 +2 +3 – 4 1011 +4 – 5 +5 – 6 +6 – 7 – 8 +7 1010 1001 0011 1000 0101 0110 0111 Figure 5. 12. Graphical interpretation of four-bit 2’s complement numbers.

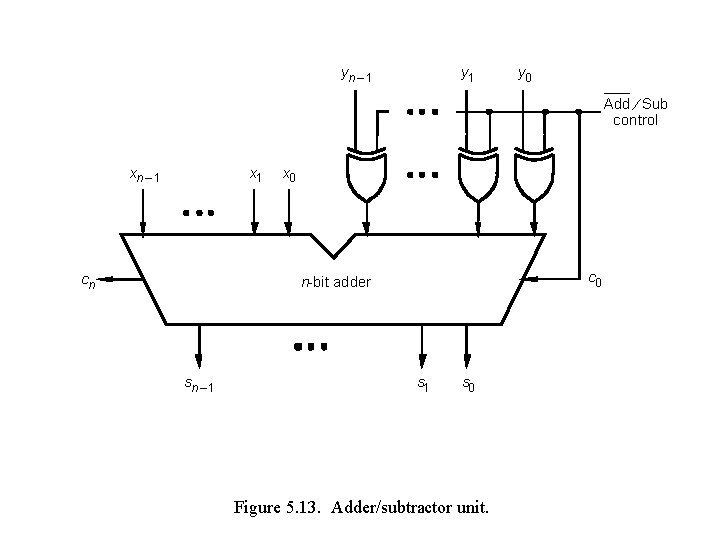
yn – 1 y 0 Add ¤ Sub control xn – 1 x 1 cn x 0 c 0 n-bit adder sn – 1 s 0 Figure 5. 13. Adder/subtractor unit.

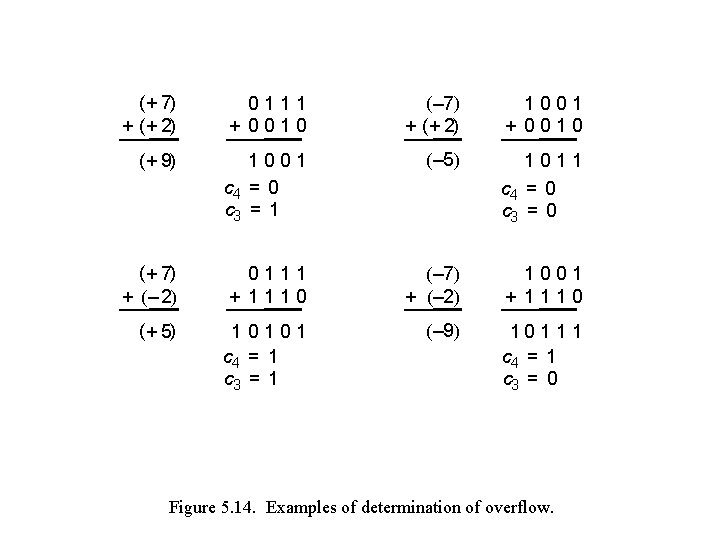
( + 7) + ( + 2) 0111 + 0010 (– 7) + ( + 2) 1001 + 0010 ( + 9) 1001 c 4 = 0 c 3 = 1 (– 5) 1011 c 4 = 0 c 3 = 0 ( + 7) + ( – 2) 0111 + 1110 (– 7) + (– 2) 1001 + 1110 ( + 5) 10101 c 4 = 1 c 3 = 1 (– 9) 10 1 1 1 c 4 = 1 c 3 = 0 Figure 5. 14. Examples of determination of overflow.

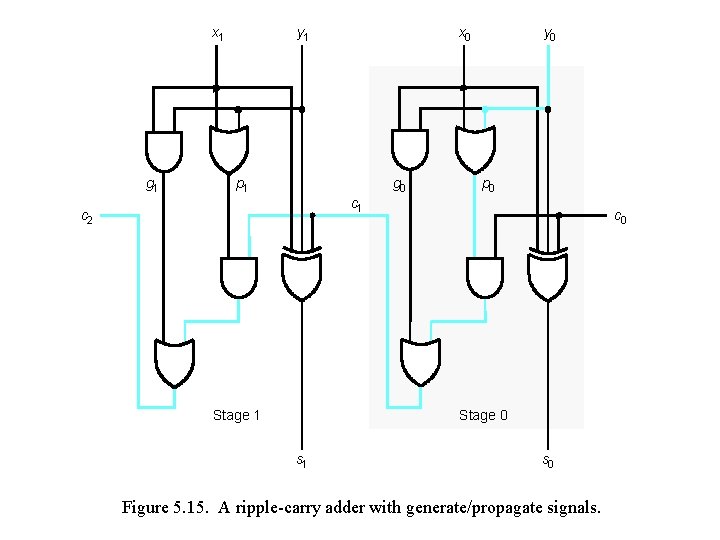
x 1 g 1 y 1 x 0 p 1 g 0 y 0 p 0 c 1 c 2 Stage 1 c 0 Stage 0 s 1 s 0 Figure 5. 15. A ripple-carry adder with generate/propagate signals.

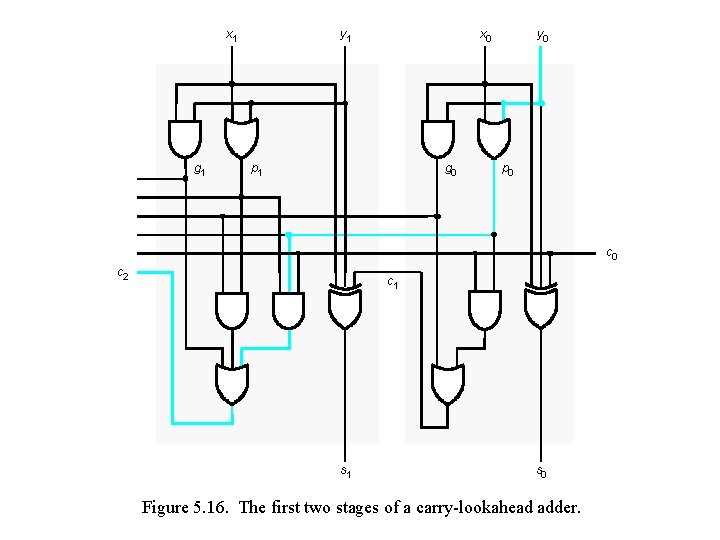
x 1 y 1 x 0 g 1 p 1 y 0 g 0 p 0 c 2 c 1 s 0 Figure 5. 16. The first two stages of a carry-lookahead adder.

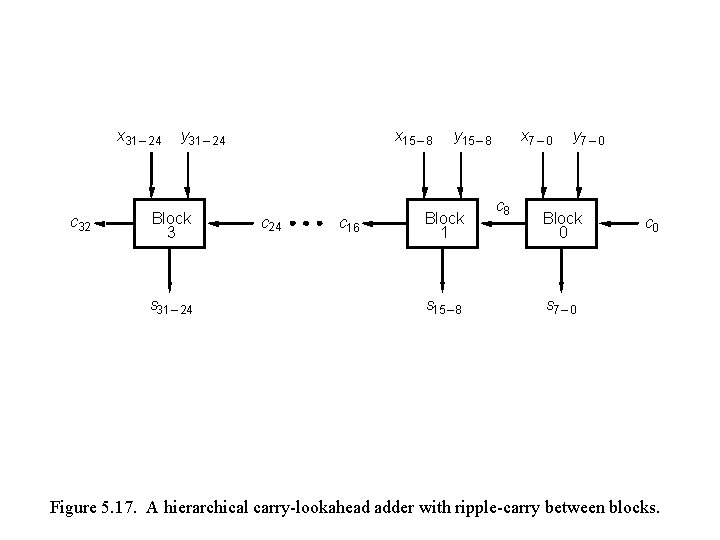
x 31 – 24 c 32 x 15 – 8 y 31 – 24 Block 3 s 31 – 24 c 16 y 15 – 8 Block 1 s 15 – 8 x 7 – 0 c 8 y 7 – 0 Block 0 c 0 s 7 – 0 Figure 5. 17. A hierarchical carry-lookahead adder with ripple-carry between blocks.

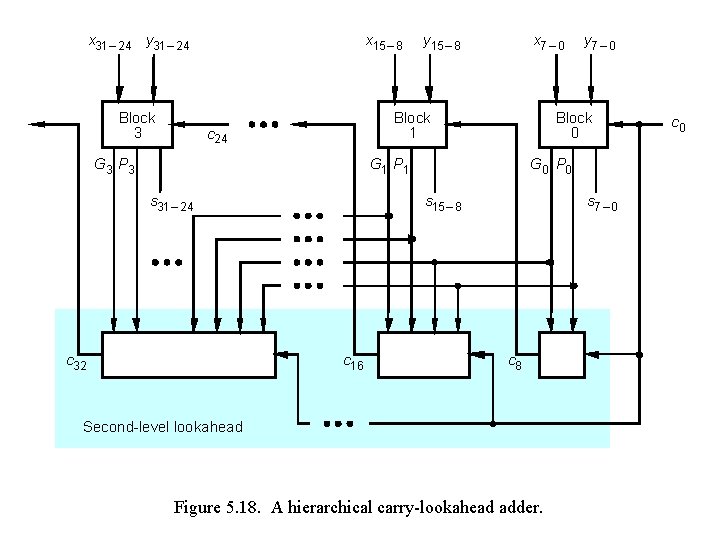
x 31 – 24 y 31 – 24 Block 3 x 15 – 8 y 15 – 8 x 7 – 0 Block 1 c 24 G 3 P 3 Block 0 G 1 P 1 s 31 – 24 c 32 G 0 P 0 s 15 – 8 c 16 y 7 – 0 s 7 – 0 c 8 Second-level lookahead Figure 5. 18. A hierarchical carry-lookahead adder. c 0

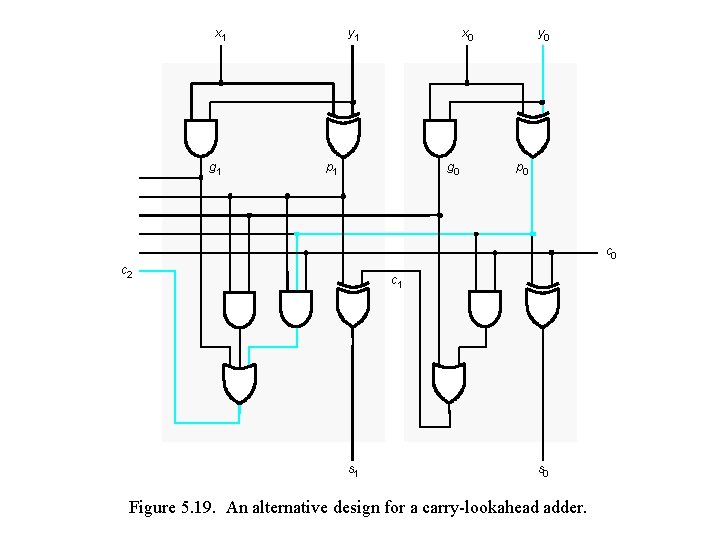
x 1 g 1 y 1 x 0 p 1 g 0 y 0 p 0 c 2 c 1 s 0 Figure 5. 19. An alternative design for a carry-lookahead adder.

Figure 5. 20. Schematic using an LPM adder/subtractor module.

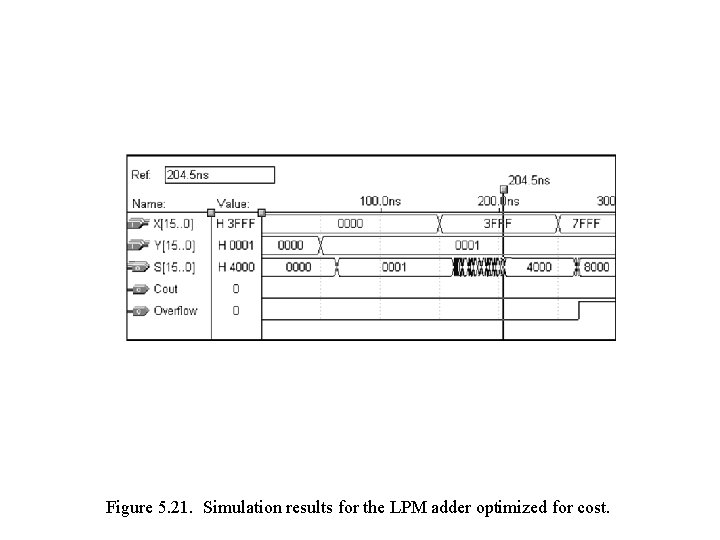
Figure 5. 21. Simulation results for the LPM adder optimized for cost.

Figure 5. 22. Simulation results for the LPM adder optimized for speed.

module fulladd (Cin, x, y, s, Cout); input Cin, x, y; output s, Cout; xor (s, x, y, Cin); and (z 1, x, y); and (z 2, x, Cin); and (z 3, y, Cin); or (Cout, z 1, z 2, z 3); endmodule Figure 5. 23. Verilog code for the full-adder using gate level primitives.

module fulladd (Cin, x, y, s, Cout); input Cin, x, y; output s, Cout; xor (s, x, y, Cin); and (z 1, x, y), (z 2, x, Cin), (z 3, y, Cin); or (Cout, z 1, z 2, z 3); endmodule Figure 5. 24. Another version of Verilog code from Figure 5. 23.

module fulladd (Cin, x, y, s, Cout); input Cin, x, y; output s, Cout; assign s = x ^ y ^ Cin; assign Cout = (x & y) | (x & Cin) | (y & Cin); endmodule Figure 5. 25. Verilog code for the full-adder using continuous assignment.

module fulladd (Cin, x, y, s, Cout); input Cin, x, y; output s, Cout; assign s = x ^ y ^ Cin, Cout = (x & y) | (x & Cin) | (y & Cin); endmodule Figure 5. 26. Another version of Verilog code from Figure 5. 25.

module adder 4 (carryin, x 3, x 2, x 1, x 0, y 3, y 2, y 1, y 0, s 3, s 2, s 1, s 0, carryout); input carryin, x 3, x 2, x 1, x 0, y 3, y 2, y 1, y 0; output s 3, s 2, s 1, s 0, carryout; fulladd stage 0 (carryin, x 0, y 0, s 0, c 1); fulladd stage 1 (c 1, x 1, y 1, s 1, c 2); fulladd stage 2 (c 2, x 2, y 2, s 2, c 3); fulladd stage 3 (c 3, x 3, y 3, s 3, carryout); endmodule fulladd (Cin, x, y, s, Cout); input Cin, x, y; output s, Cout; assign s = x ^ y ^ Cin, assign Cout = (x & y) | (x & Cin) | (y & Cin); endmodule Figure 5. 27. Verilog code for a four-bit adder.

module adder 4 (carryin, X, Y, S, carryout); input carryin; input [3: 0] X, Y; output [3: 0] S; output carryout; wire [3: 1] C; fulladd stage 0 (carryin, X[0], Y[0], S[0], C[1]); fulladd stage 1 (C[1], X[1], Y[1], S[1], C[2]); fulladd stage 2 (C[2], X[2], Y[2], S[2], C[3]); fulladd stage 3 (C[3], X[3], Y[3], S[3], carryout); endmodule Figure 5. 28. A four-bit adder using vectors.

module addern (carryin, X, Y, S, carryout); parameter n=32; input carryin; input [n-1: 0] X, Y; output [n-1: 0] S; output carryout; reg [n-1: 0] S; reg carryout; reg [n: 0] C; integer k; always @(X or Y or carryin) begin C[0] = carryin; for (k = 0; k < n; k = k+1) begin S[k] = X[k] ^ Y[k] ^ C[k]; C[k+1] = (X[k] & Y[k]) | (X[k] & C[k]) | (Y[k] & C[k]); end carryout = C[n]; endmodule Figure 5. 29. A generic specification of a ripple-carry adder.

module addern (carryin, X, Y, S); parameter n = 32; input carryin; input [n-1: 0] X, Y; output [n-1: 0] S; reg [n-1: 0] S; always @(X or Y or carryin) S = X + Y + carryin; endmodule Figure 5. 30. Specification of an n-bit adder using arithmetic assignment.

module addern (carryin, X, Y, S, carryout, overflow); parameter n = 32; input carryin; input [n-1: 0] X, Y; output [n-1: 0] S; output carryout, overflow; reg [n-1: 0] S; reg carryout, overflow; always @(X or Y or carryin) begin S = X + Y + carryin; carryout = (X[n-1] & Y[n-1]) | (X[n-1] & ~S[n-1]) | (Y[n-1] & ~S[n-1]); overflow = carryout ^ X[n-1] ^ Y[n-1] ^ S[n-1]; endmodule Figure 5. 31. An n-bit adder with carry-out and overflow signals.

module addern (carryin, X, Y, S, carryout, overflow); parameter n = 32; input carryin; input [n-1: 0] X, Y; output [n-1: 0] S; output carryout, overflow; reg [n-1: 0] S; reg carryout, overflow; reg [n: 0] Sum; always @(X or Y or carryin) begin Sum = {1'b 0, X} + {1'b 0, Y} + carryin; S = Sum[n-1: 0]; carryout = Sum[n]; overflow = carryout ^ X[n-1] ^ Y[n-1] ^ S[n-1]; endmodule Figure 5. 32. An alternative specification of an n-bit adder with carry-out and overflow signals.

module addern (carryin, X, Y, S, carryout, overflow); parameter n = 32; input carryin; input [n-1: 0] X, Y; output [n-1: 0] S; output carryout, overflow; reg [n-1: 0] S; reg carryout, overflow; always @(X or Y or carryin) begin {carryout, S} = X + Y + carryin; overflow = carryout ^ X[n-1] ^ Y[n-1] ^ S[n-1]; endmodule Figure 5. 33. Simplified complete specification of an n-bit adder.

module fulladd (Cin, x, y, s, Cout); input Cin, x, y; output s, Cout; reg s, Cout; always @(x or y or Cin) {Cout, s} = x + y + Cin; endmodule Figure 5. 34. Behavioral specification of a full-adder.

Please see “portrait orientation” Power. Point file for Chapter 5 Figure 5. 35. Multiplication of unsigned numbers.

Please see “portrait orientation” Power. Point file for Chapter 5 Figure 5. 36. A 4 x 4 multiplier circuit.

Please see “portrait orientation” Power. Point file for Chapter 5 Figure 5. 37. Multiplication of signed numbers.

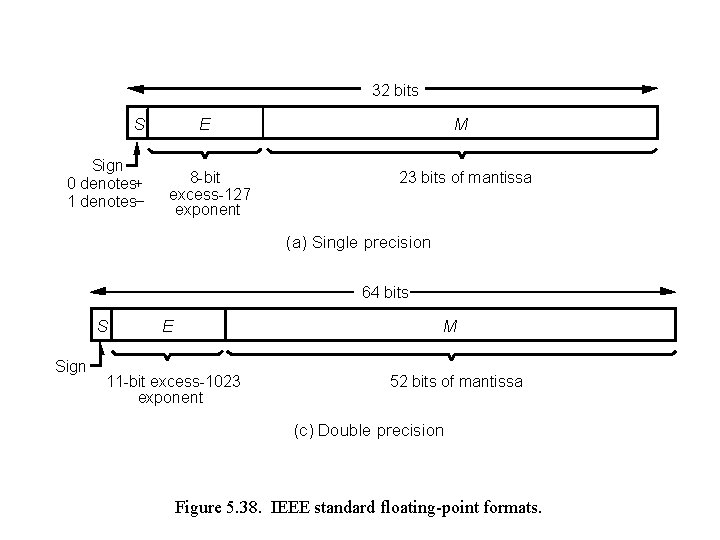
32 bits S Sign 0 denotes+ 1 denotes– E 8 -bit excess-127 exponent M 23 bits of mantissa (a) Single precision 64 bits S Sign M E 11 -bit excess-1023 exponent 52 bits of mantissa (c) Double precision Figure 5. 38. IEEE standard floating-point formats.

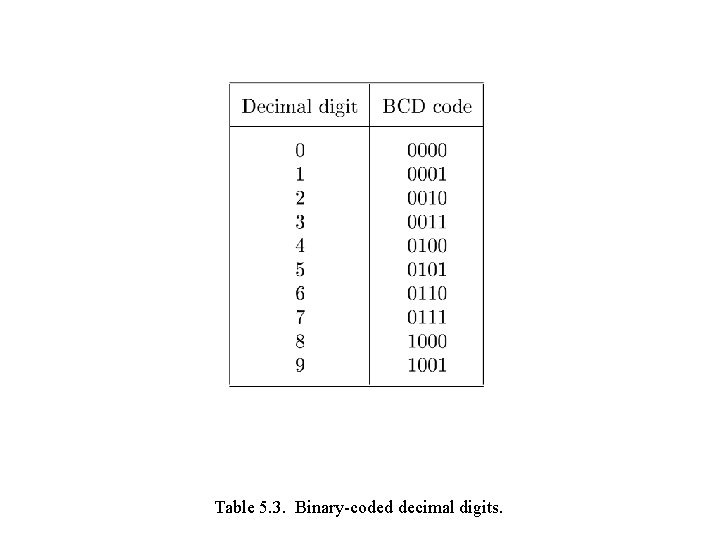
Table 5. 3. Binary-coded decimal digits.

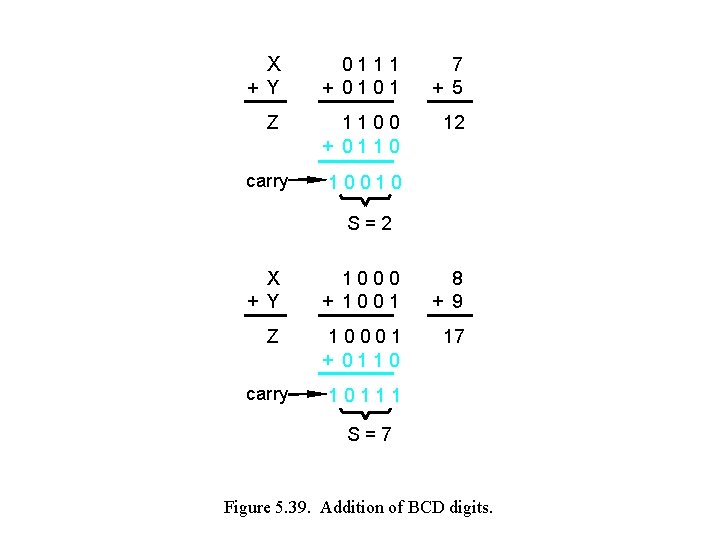
X + Y Z carry 0111 + 0101 7 + 5 1100 + 0110 12 10010 S=2 X + Y 1000 + 1001 8 + 9 Z 10001 + 0110 17 carry 10111 S=7 Figure 5. 39. Addition of BCD digits.

Figure 5. 40. Block diagram for a one-digit BCD adder.

module bcdadd (Cin, X, Y, S, Cout); input Cin; input [3: 0] X, Y; output [3: 0] S; output Cout; reg [3: 0] S; reg Cout; reg [4: 0] Z; always@ (X or Y or Cin) begin Z = X + Y + Cin; if (Z < 10) {Cout, S} = Z; else {Cout, S} = Z + 6; endmodule Figure 5. 41. Verilog code for a one-digit BCD adder.

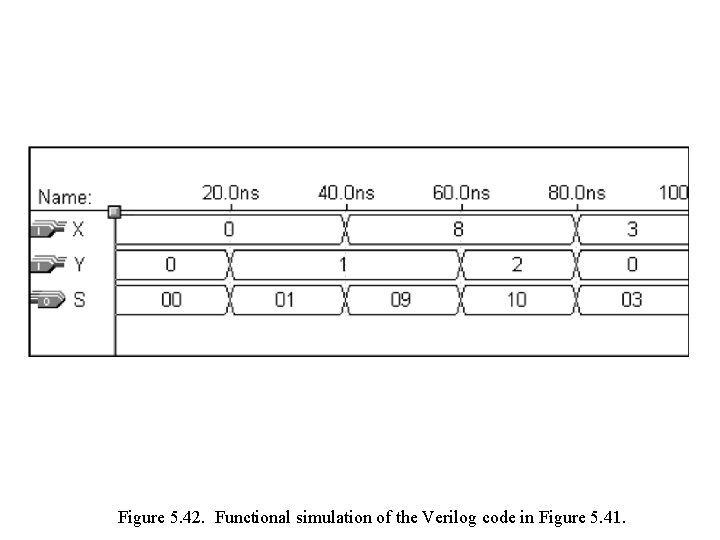
Figure 5. 42. Functional simulation of the Verilog code in Figure 5. 41.

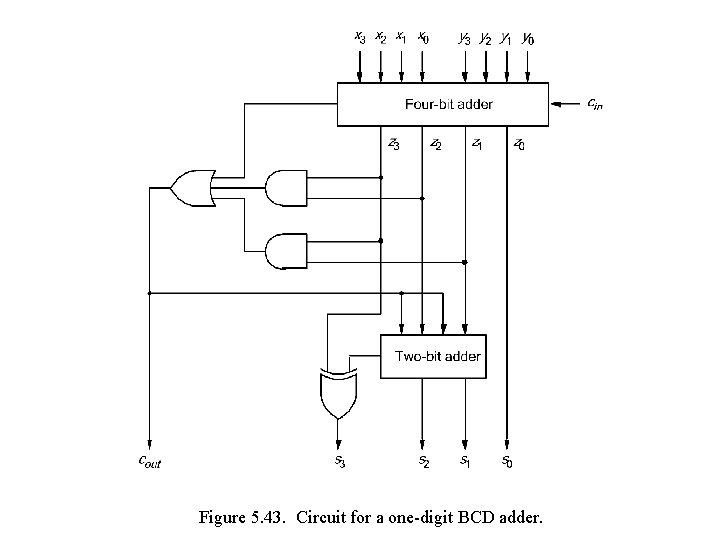
Figure 5. 43. Circuit for a one-digit BCD adder.

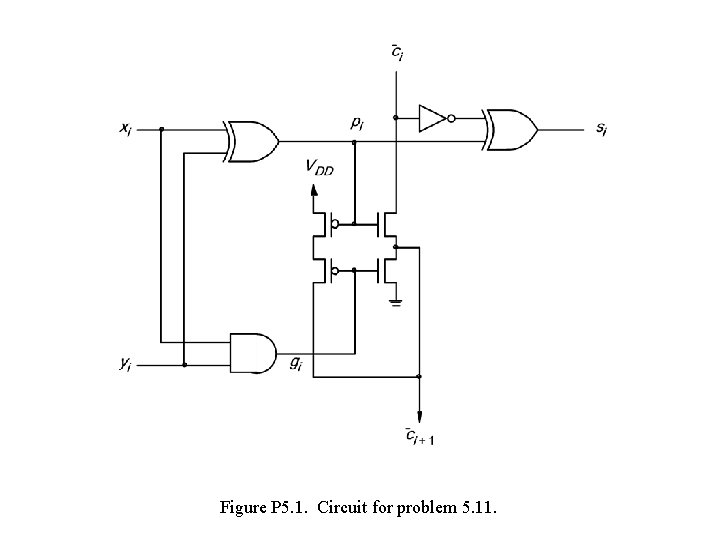
Figure P 5. 1. Circuit for problem 5. 11.

module problem 5_17 (IN, OUT); input [3: 0] IN; output [3: 0] OUT; reg [3: 0] OUT; always @(IN) if (IN == 4'b 0101) OUT = 4'b 0001; else if (IN == 4'b 0110) OUT = 4'b 0010; else if (IN == 4'b 0111) OUT = 4'b 0011; else if (IN == 4'b 1001) OUT = 4'b 0010; else if (IN == 4'b 1010) OUT = 4'b 0100; else if (IN == 4'b 1011) OUT = 4'b 0110; else if (IN == 4'b 1101) OUT = 4'b 0011; else if (IN == 4'b 1110) OUT = 4'b 0110; else if (IN == 4'b 1111) OUT = 4'b 1001; else OUT = 4'b 0000; endmodule Figure P 5. 2. The code for problem 5. 17.

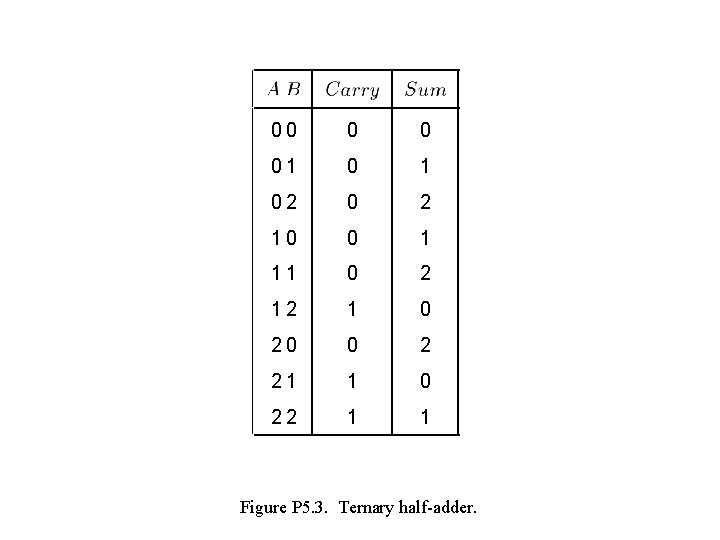
00 0 0 01 0 1 02 0 2 10 0 1 11 0 2 12 1 0 20 0 2 21 1 0 22 1 1 Figure P 5. 3. Ternary half-adder.