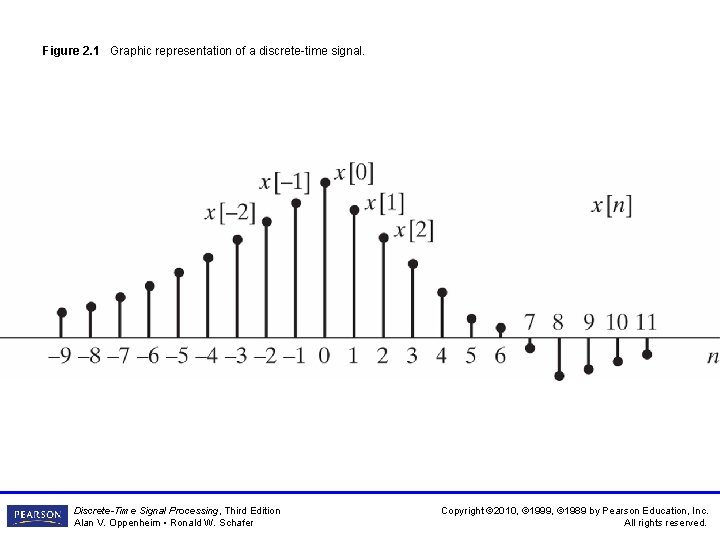
Figure 2 1 Graphic representation of a discretetime


![Figure 2. 9 Forming the sequence h[n − k]. (a) The sequence h[k] as Figure 2. 9 Forming the sequence h[n − k]. (a) The sequence h[k] as](https://slidetodoc.com/presentation_image/33691aff46169078bac5a9a5647b65ed/image-9.jpg)
![Figure 2. 10 Sequence involved in computing a discrete convolution. (a)–(c) The sequences x[k] Figure 2. 10 Sequence involved in computing a discrete convolution. (a)–(c) The sequences x[k]](https://slidetodoc.com/presentation_image/33691aff46169078bac5a9a5647b65ed/image-10.jpg)




![Figure 2. 22 Frequency response for a system with impulse response h[n] = anu[n]. Figure 2. 22 Frequency response for a system with impulse response h[n] = anu[n].](https://slidetodoc.com/presentation_image/33691aff46169078bac5a9a5647b65ed/image-23.jpg)


- Slides: 63

Figure 2. 1 Graphic representation of a discrete-time signal. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Figure 2. 2 (a) Segment of a continuous-time speech signal xa(t ). (b) Sequence of samples x[n] = xa(n. T ) obtained from the signal in part (a) with T = 125 µs. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

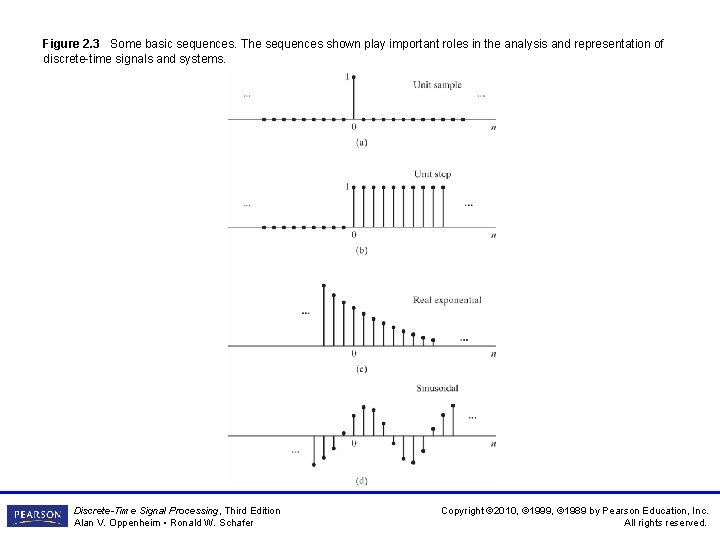
Figure 2. 3 Some basic sequences. The sequences shown play important roles in the analysis and representation of discrete-time signals and systems. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

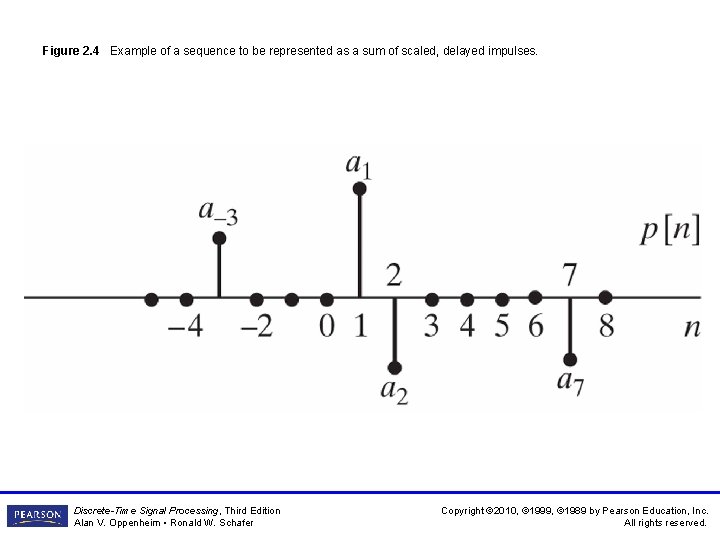
Figure 2. 4 Example of a sequence to be represented as a sum of scaled, delayed impulses. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Figure 2. 5 cos ω0 n for several different values of ω0. As ω0 increases from zero toward π (parts a-d), the sequence oscillates more rapidly. As ω0 increases from π to 2π (parts d-a), the oscillations become slower. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

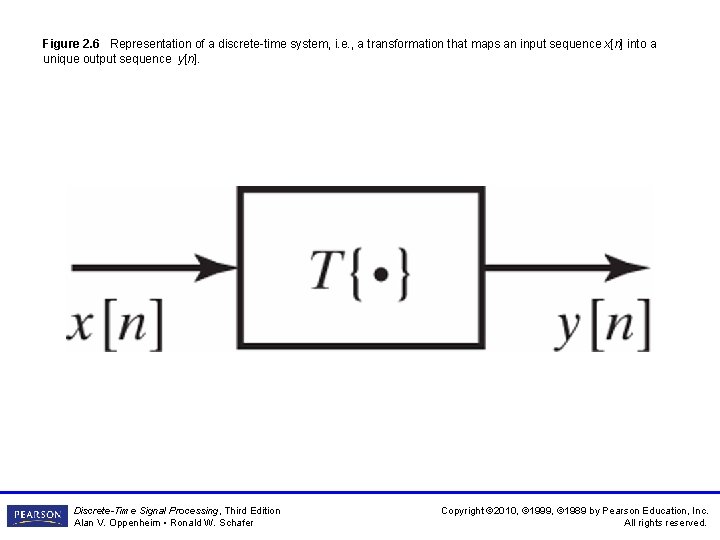
Figure 2. 6 Representation of a discrete-time system, i. e. , a transformation that maps an input sequence x[n] into a unique output sequence y[n]. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

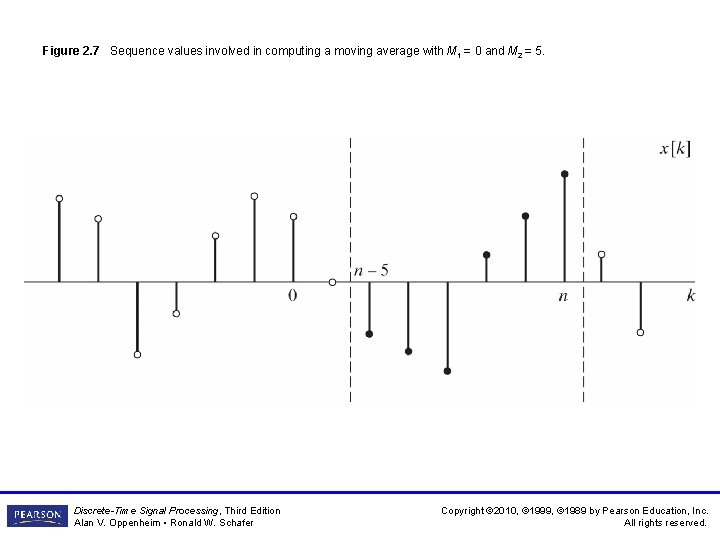
Figure 2. 7 Sequence values involved in computing a moving average with M 1 = 0 and M 2 = 5. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

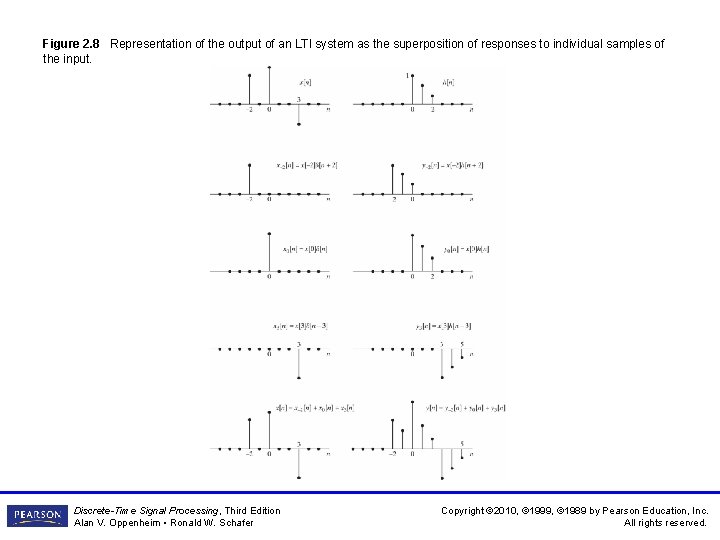
Figure 2. 8 Representation of the output of an LTI system as the superposition of responses to individual samples of the input. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.
![Figure 2 9 Forming the sequence hn k a The sequence hk as Figure 2. 9 Forming the sequence h[n − k]. (a) The sequence h[k] as](https://slidetodoc.com/presentation_image/33691aff46169078bac5a9a5647b65ed/image-9.jpg)
Figure 2. 9 Forming the sequence h[n − k]. (a) The sequence h[k] as a function of k. (b) The sequence h[−k] as a function of k. (c) The sequence h[n − k] = h[ − (k − n)] as a function of k for n = 4. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.
![Figure 2 10 Sequence involved in computing a discrete convolution ac The sequences xk Figure 2. 10 Sequence involved in computing a discrete convolution. (a)–(c) The sequences x[k]](https://slidetodoc.com/presentation_image/33691aff46169078bac5a9a5647b65ed/image-10.jpg)
Figure 2. 10 Sequence involved in computing a discrete convolution. (a)–(c) The sequences x[k] and h[n− k] as a function of k for different values of n. (Only nonzero samples are shown. ) (d) Corresponding output sequence as a function of n. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

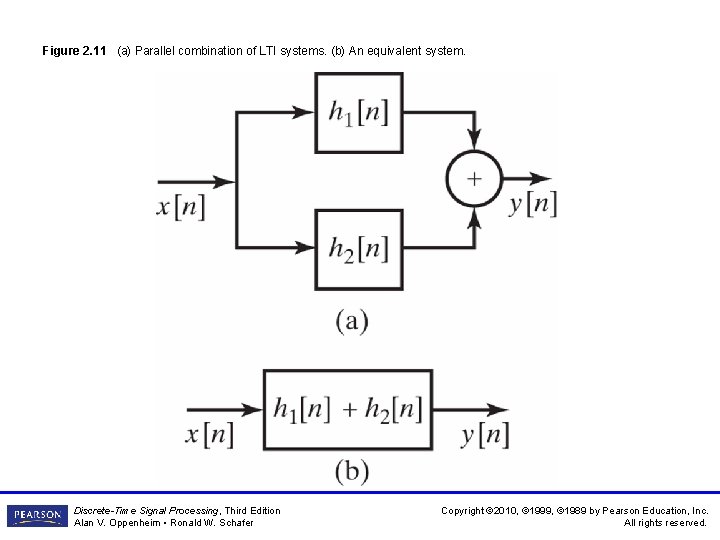
Figure 2. 11 (a) Parallel combination of LTI systems. (b) An equivalent system. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

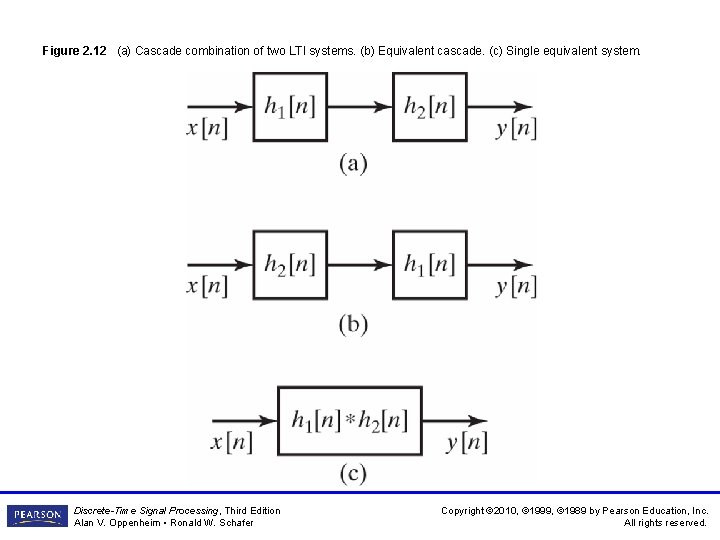
Figure 2. 12 (a) Cascade combination of two LTI systems. (b) Equivalent cascade. (c) Single equivalent system. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

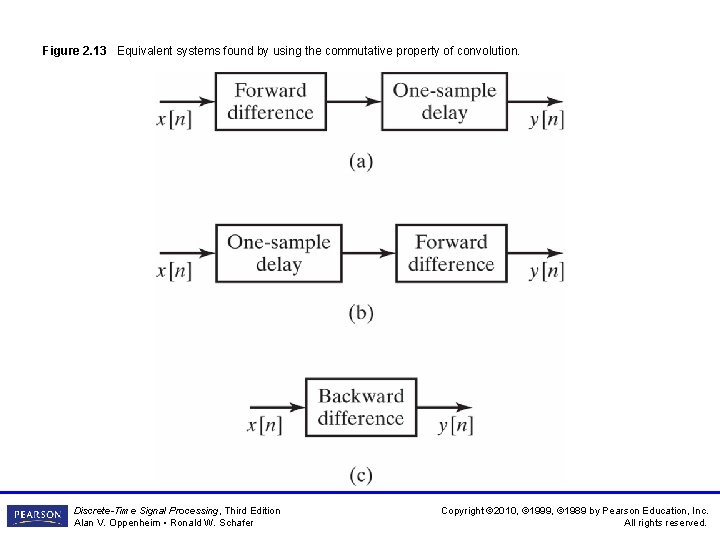
Figure 2. 13 Equivalent systems found by using the commutative property of convolution. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

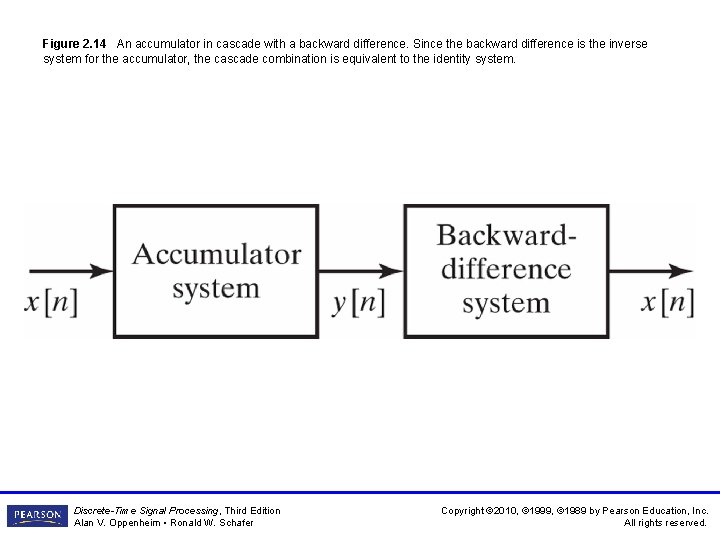
Figure 2. 14 An accumulator in cascade with a backward difference. Since the backward difference is the inverse system for the accumulator, the cascade combination is equivalent to the identity system. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

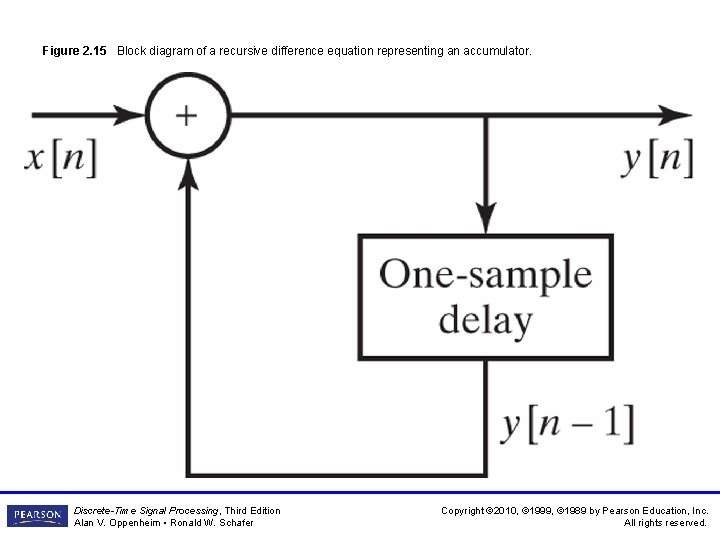
Figure 2. 15 Block diagram of a recursive difference equation representing an accumulator. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

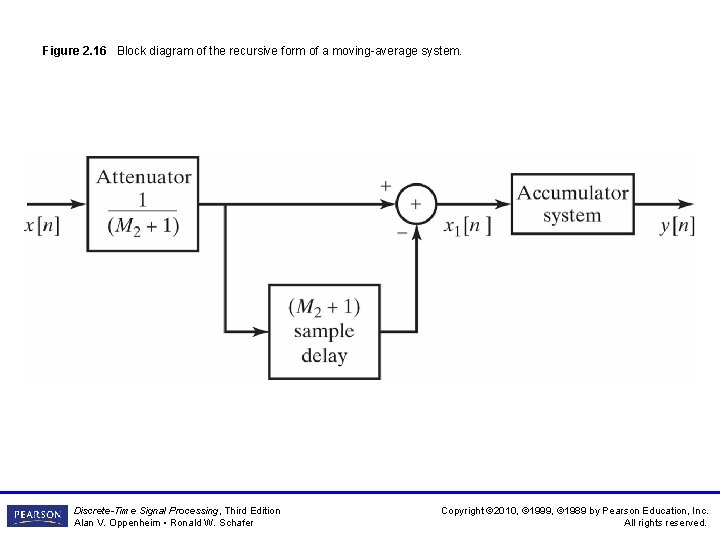
Figure 2. 16 Block diagram of the recursive form of a moving-average system. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

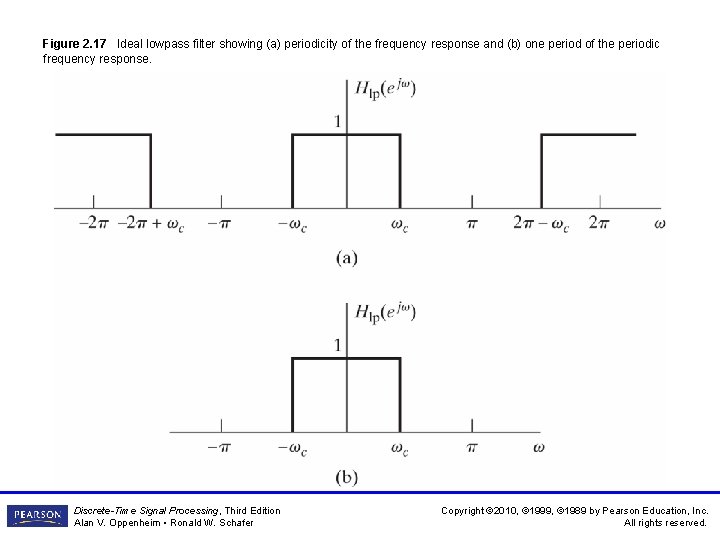
Figure 2. 17 Ideal lowpass filter showing (a) periodicity of the frequency response and (b) one period of the periodic frequency response. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Figure 2. 18 Ideal frequency-selective filters. (a) Highpass filter. (b) Bandstop filter. (c) Bandpass filter. In each case, the frequency response is periodic with period 2π. Only one period is shown. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

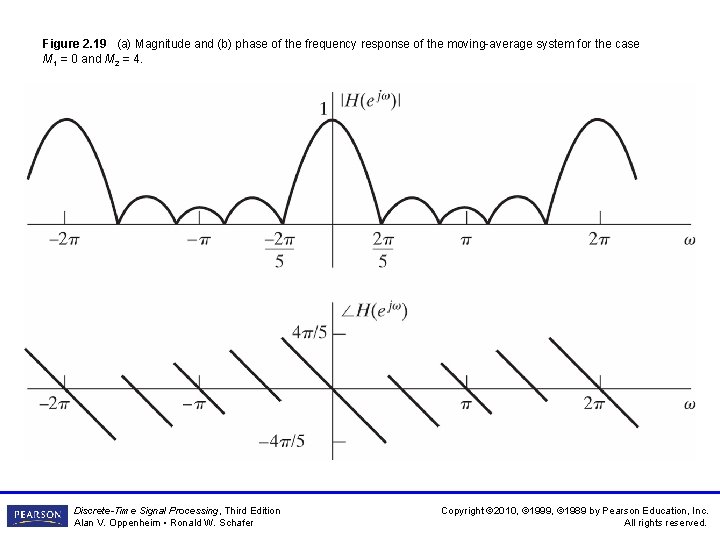
Figure 2. 19 (a) Magnitude and (b) phase of the frequency response of the moving-average system for the case M 1 = 0 and M 2 = 4. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Figure 2. 20 Illustration of a real part of suddenly applied complex exponential input with (a) FIR and (b) IIR. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Figure 2. 21 Convergence of the Fourier transform. The oscillatory behavior at ω = ωc is often called the Gibbs phenomenon. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Table 2. 1 SYMMETRY PROPERTIES OF THE FOURIER TRANSFORM Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.
![Figure 2 22 Frequency response for a system with impulse response hn anun Figure 2. 22 Frequency response for a system with impulse response h[n] = anu[n].](https://slidetodoc.com/presentation_image/33691aff46169078bac5a9a5647b65ed/image-23.jpg)
Figure 2. 22 Frequency response for a system with impulse response h[n] = anu[n]. (a) Real part. a > 0; a = 0. 75 (solid curve) and a = 0. 5 (dashed curve). (b) Imaginary part. (c) Magnitude. a > 0; a = 0. 75 (solid curve) and a = 0. 5 (dashed curve). (d) Phase. Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Table 2. 2 FOURIER TRANSFORM THEOREMS Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

Table 2. 3 FOURIER TRANSFORM PAIRS Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

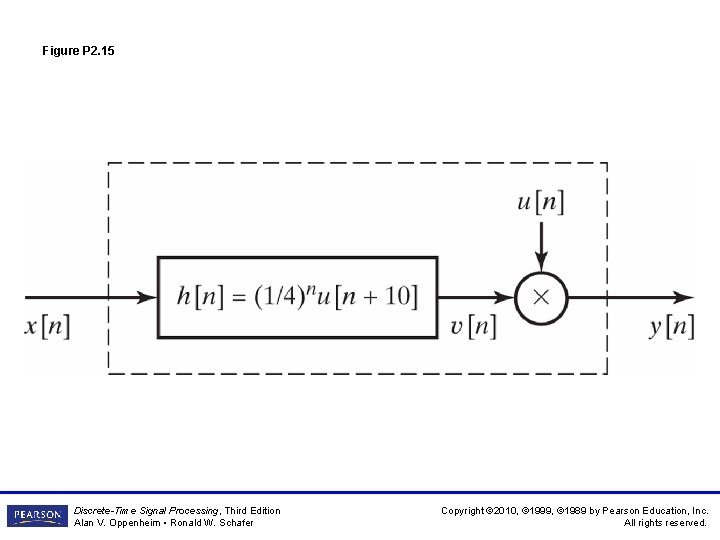
Figure P 2. 15 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

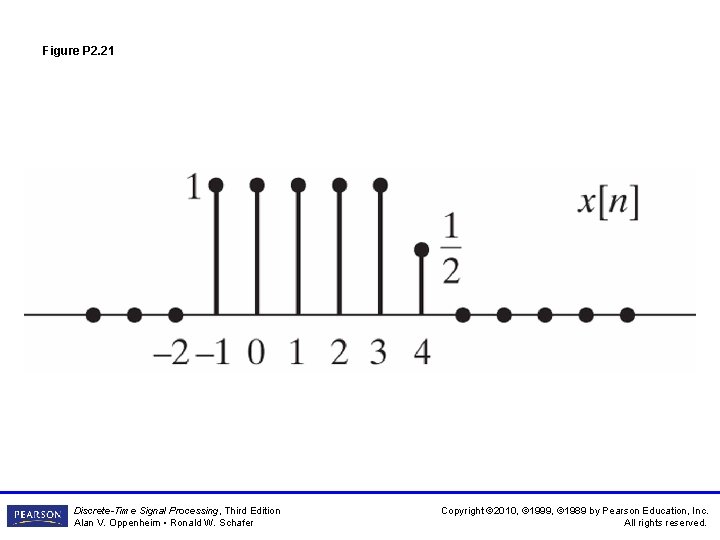
Figure P 2. 21 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

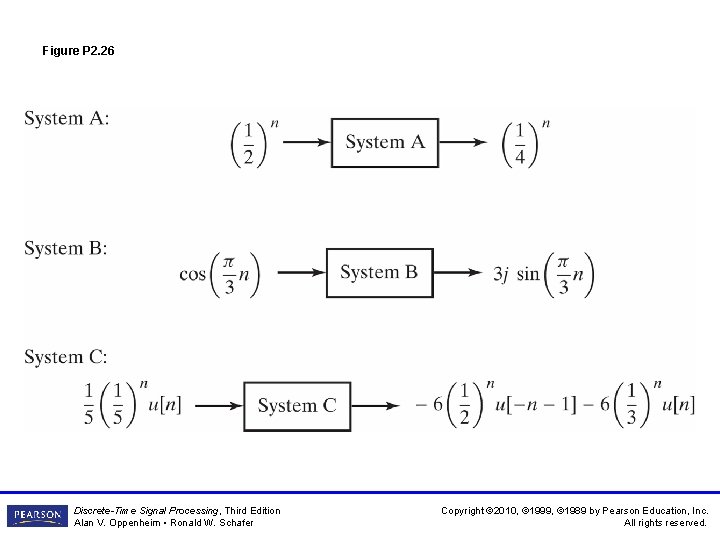
Figure P 2. 26 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

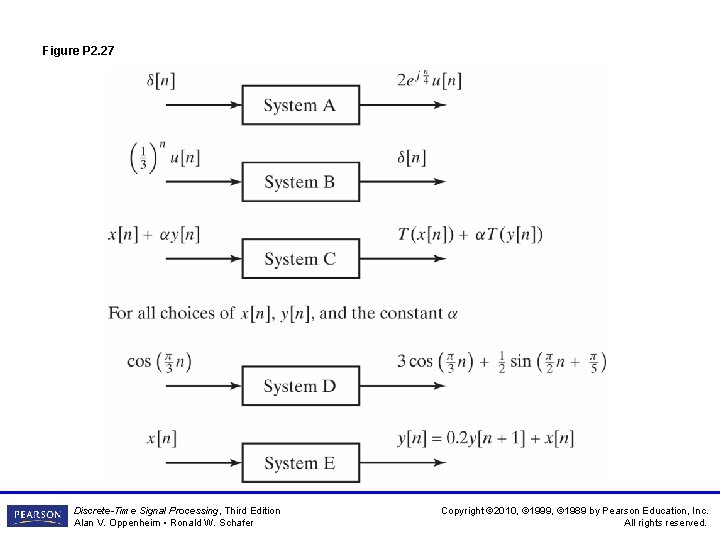
Figure P 2. 27 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

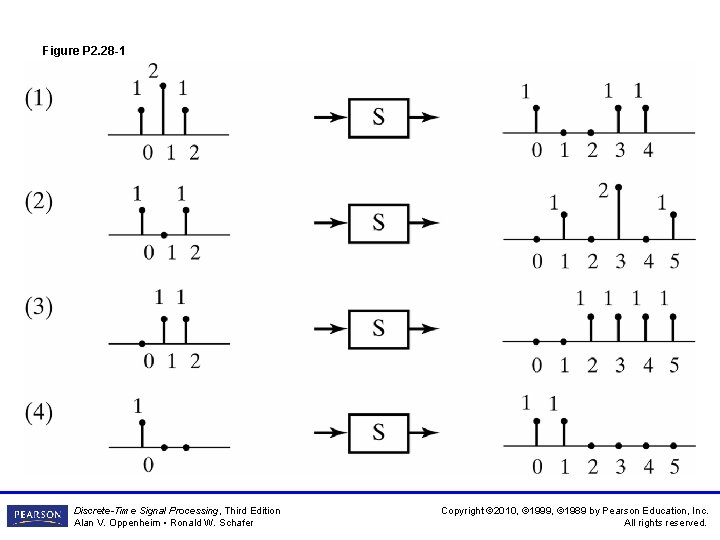
Figure P 2. 28 -1 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

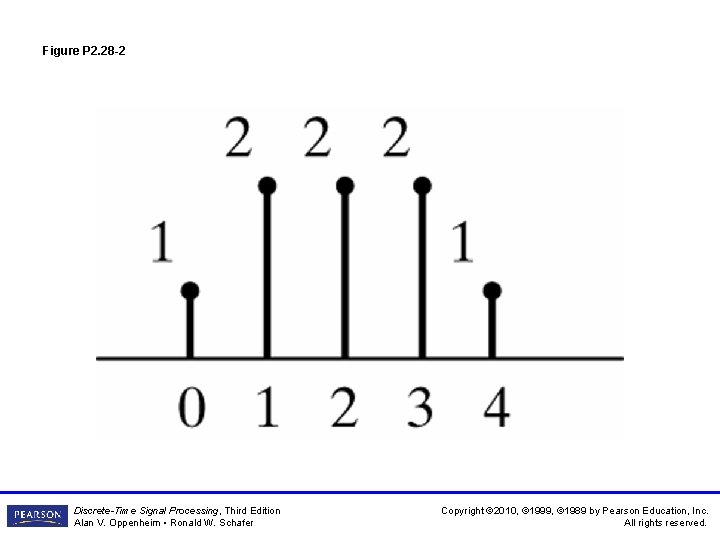
Figure P 2. 28 -2 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

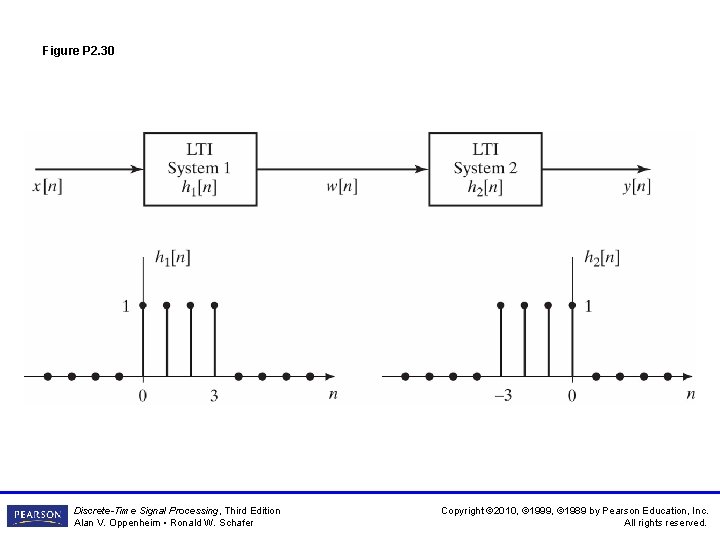
Figure P 2. 30 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

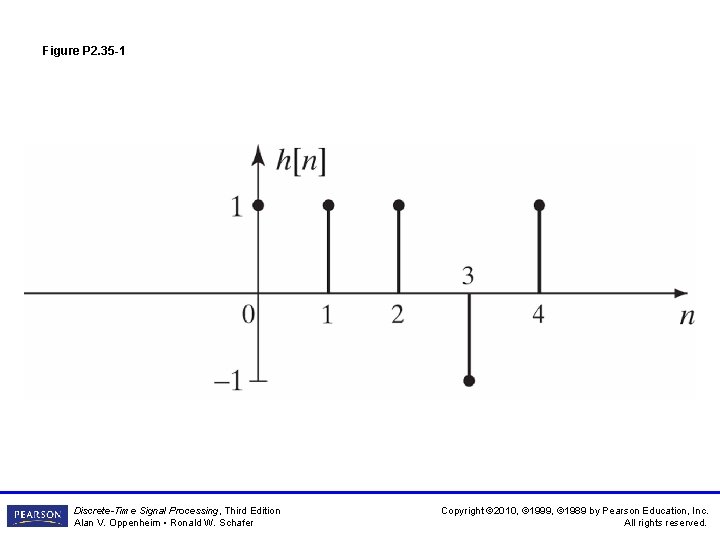
Figure P 2. 35 -1 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

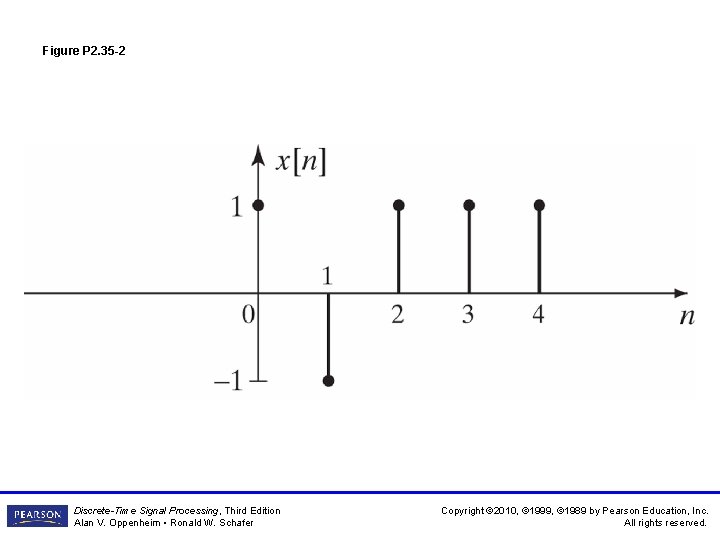
Figure P 2. 35 -2 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

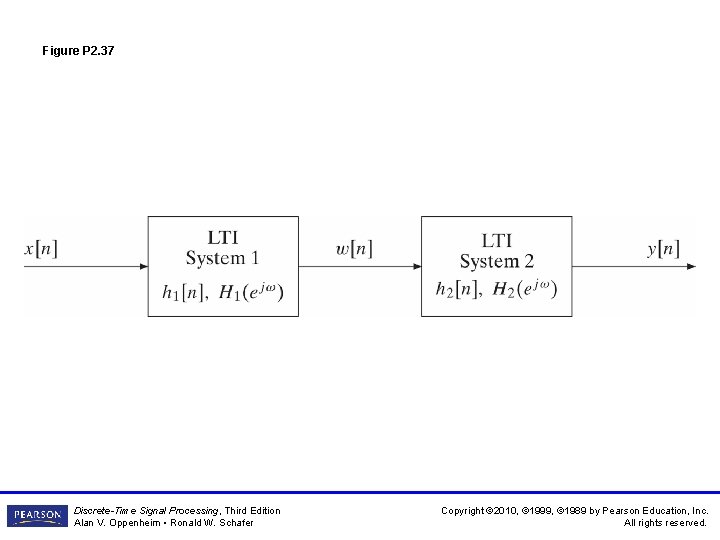
Figure P 2. 37 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

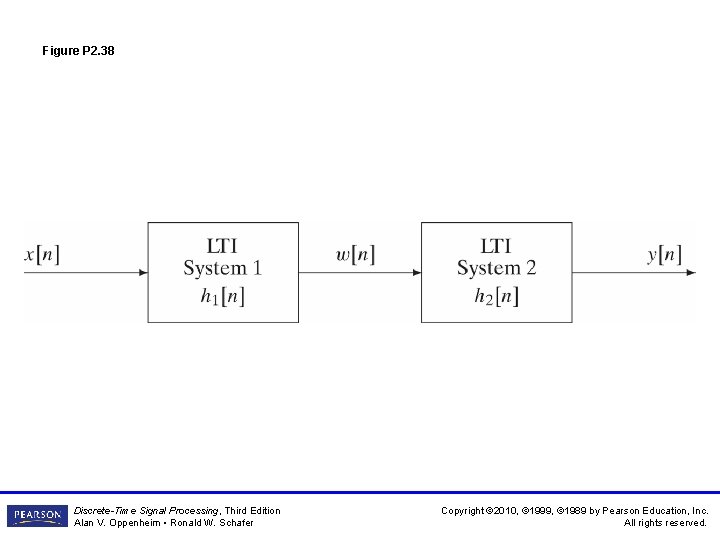
Figure P 2. 38 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

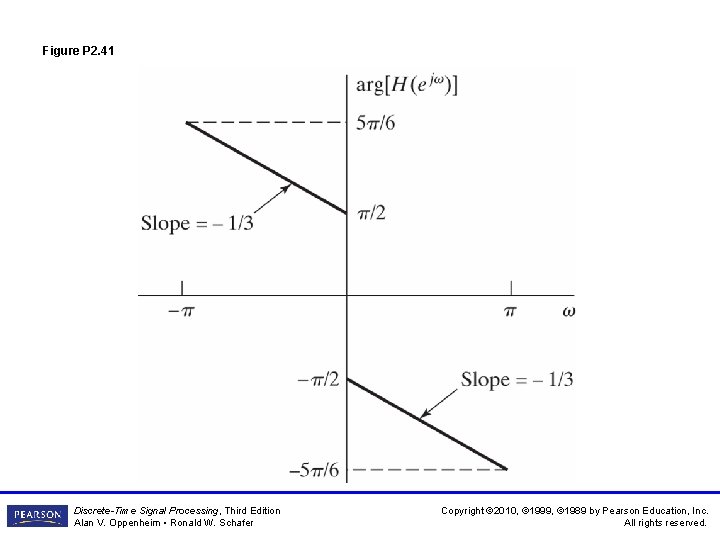
Figure P 2. 41 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

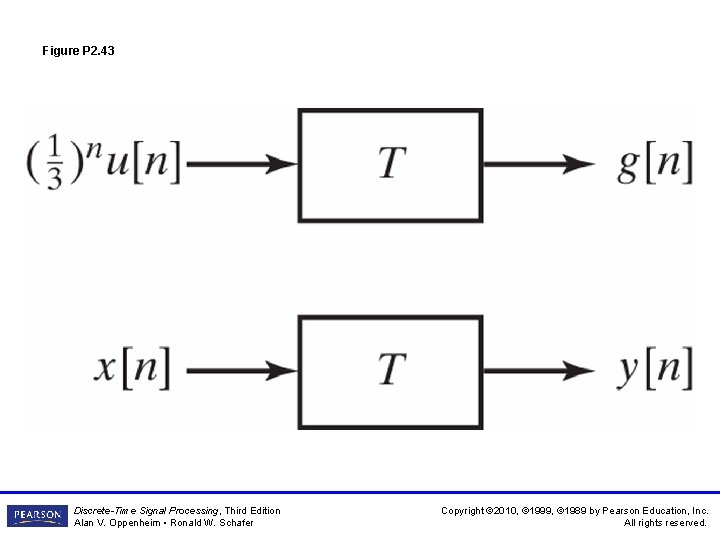
Figure P 2. 43 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

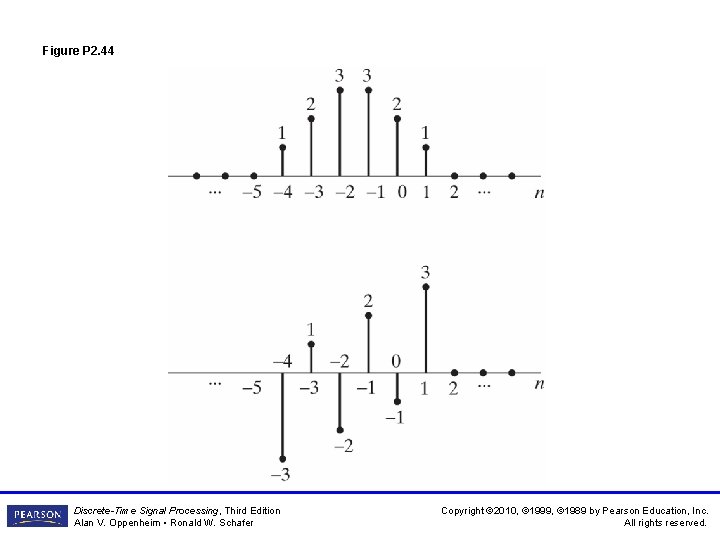
Figure P 2. 44 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

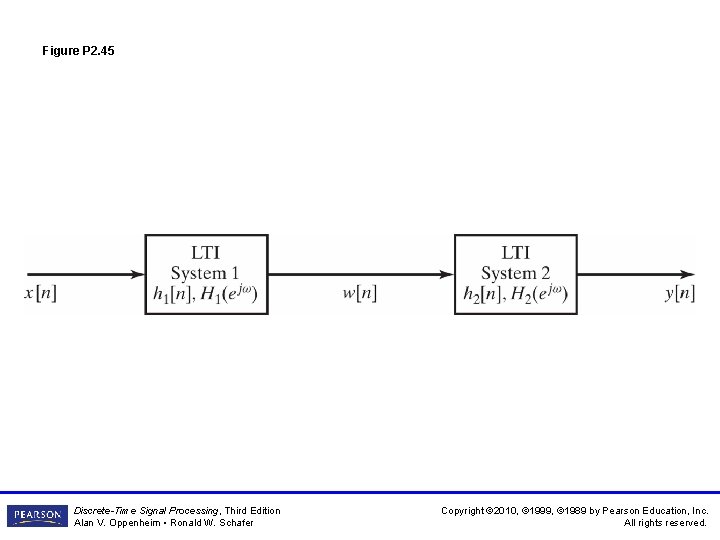
Figure P 2. 45 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

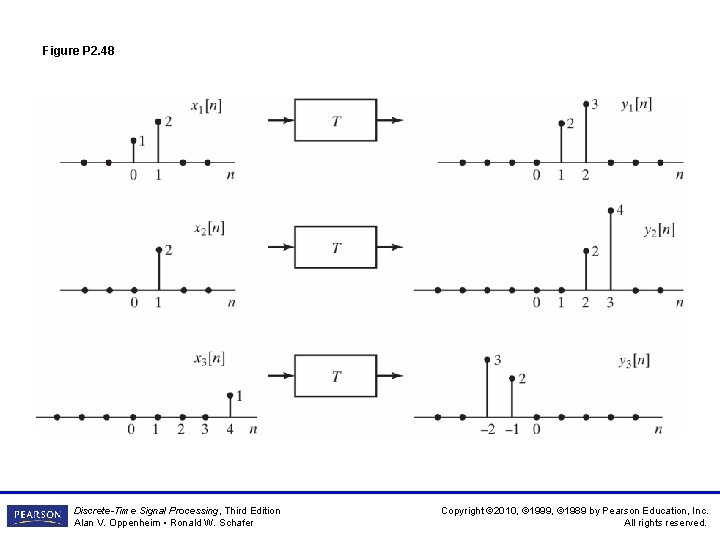
Figure P 2. 48 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

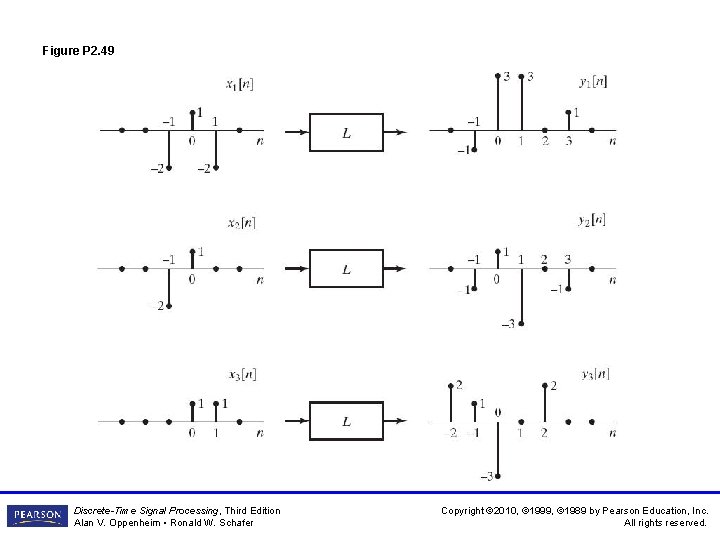
Figure P 2. 49 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

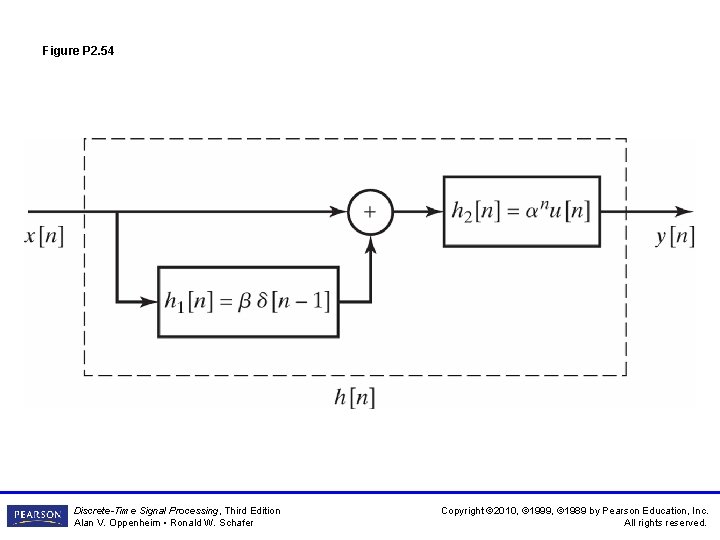
Figure P 2. 54 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

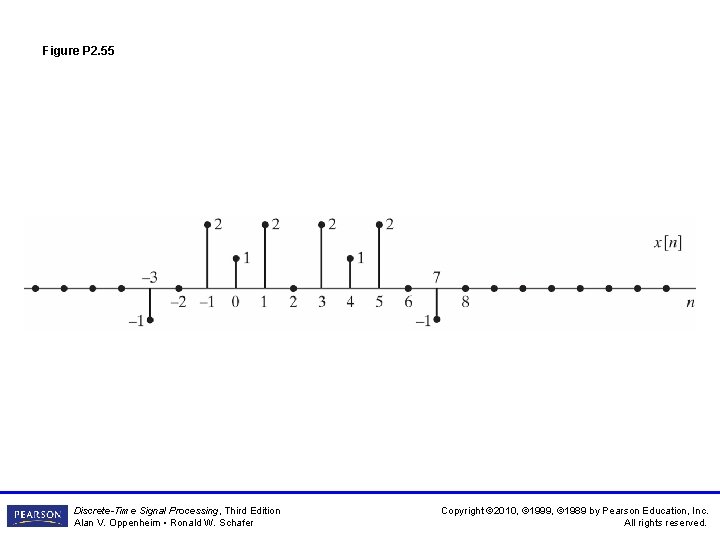
Figure P 2. 55 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

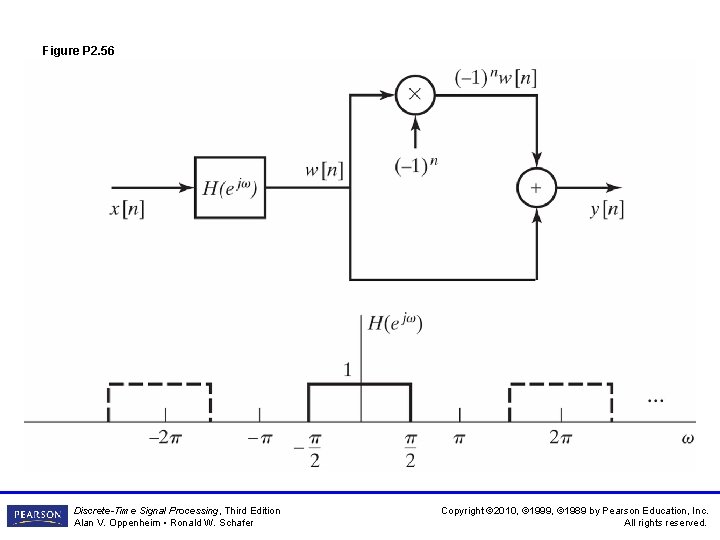
Figure P 2. 56 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

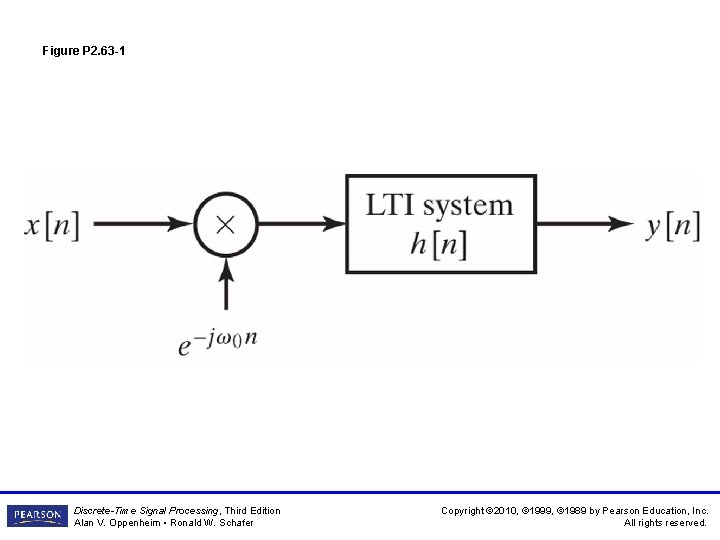
Figure P 2. 63 -1 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

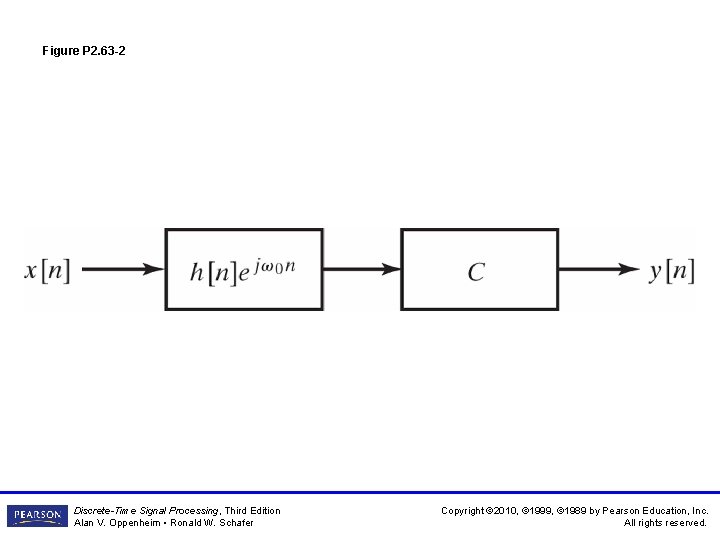
Figure P 2. 63 -2 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

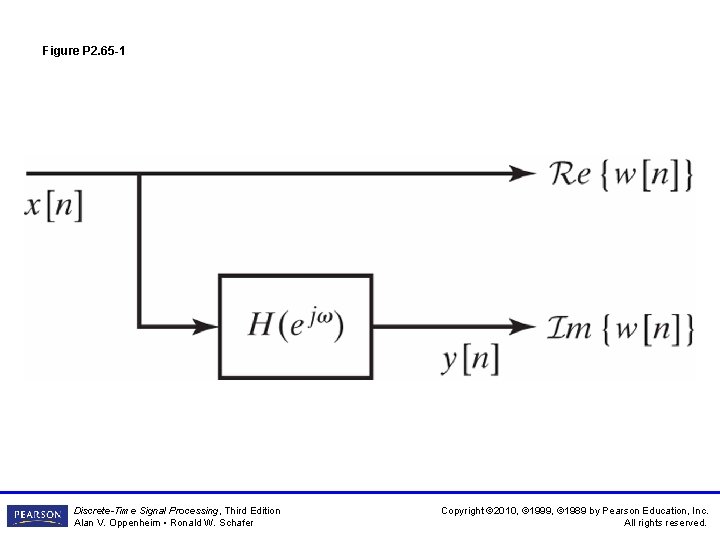
Figure P 2. 65 -1 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

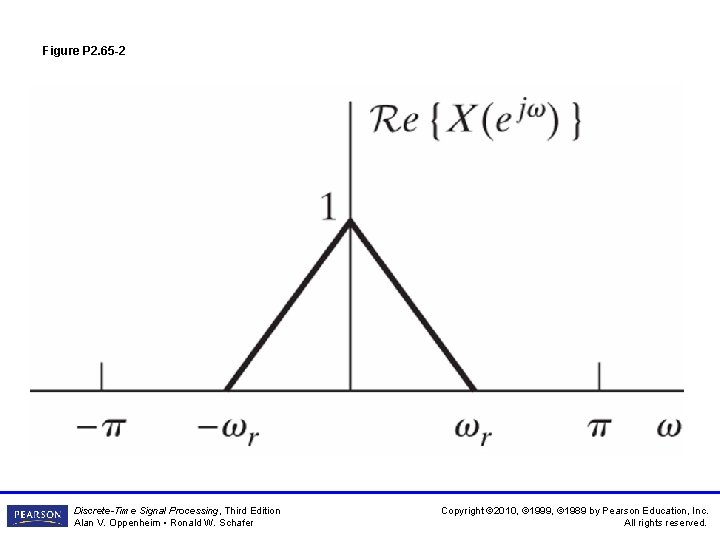
Figure P 2. 65 -2 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

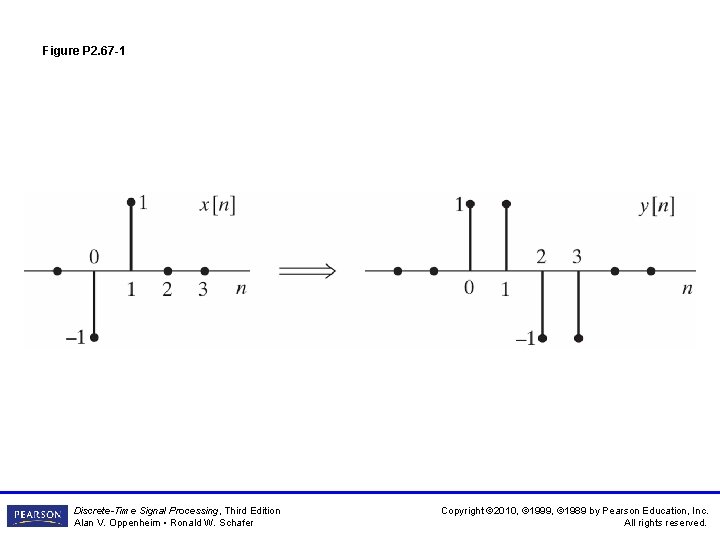
Figure P 2. 67 -1 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

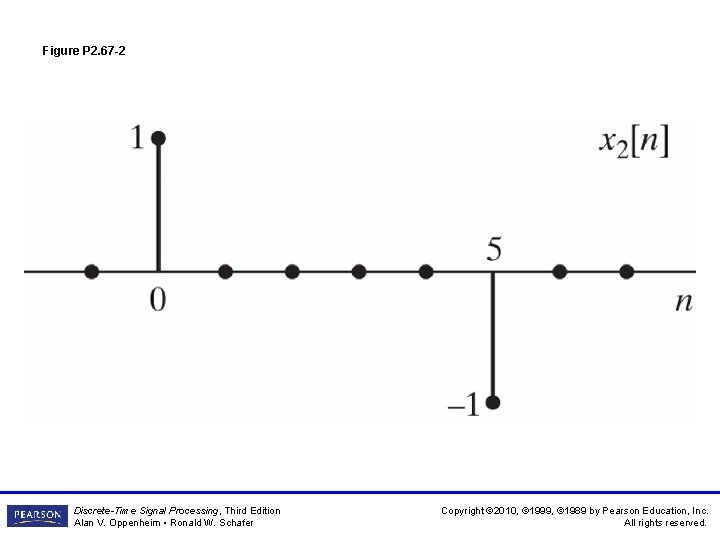
Figure P 2. 67 -2 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

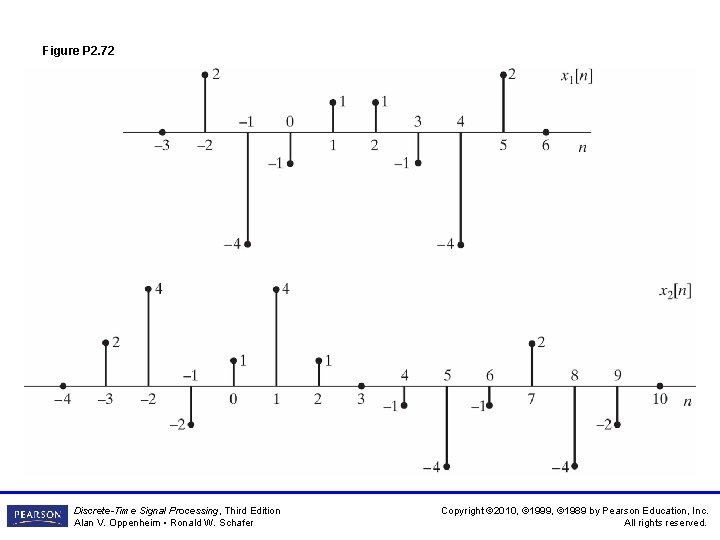
Figure P 2. 72 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

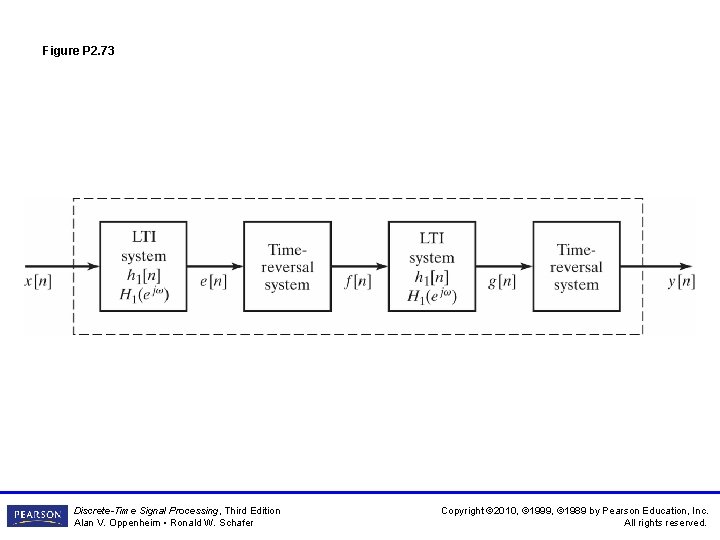
Figure P 2. 73 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

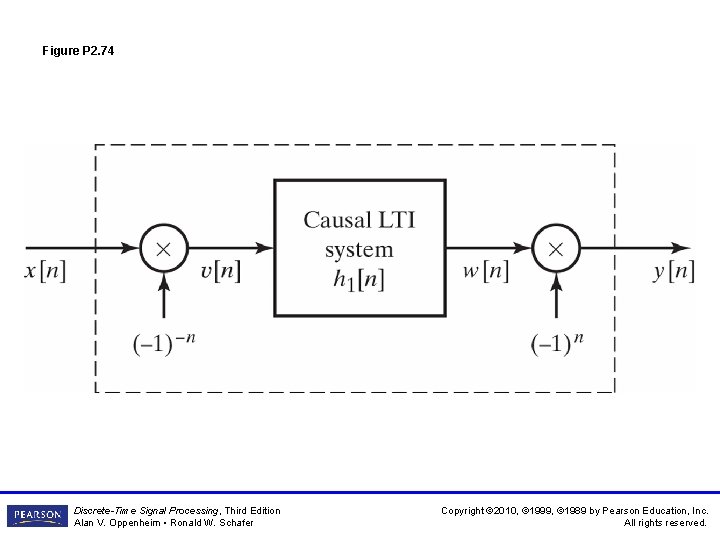
Figure P 2. 74 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

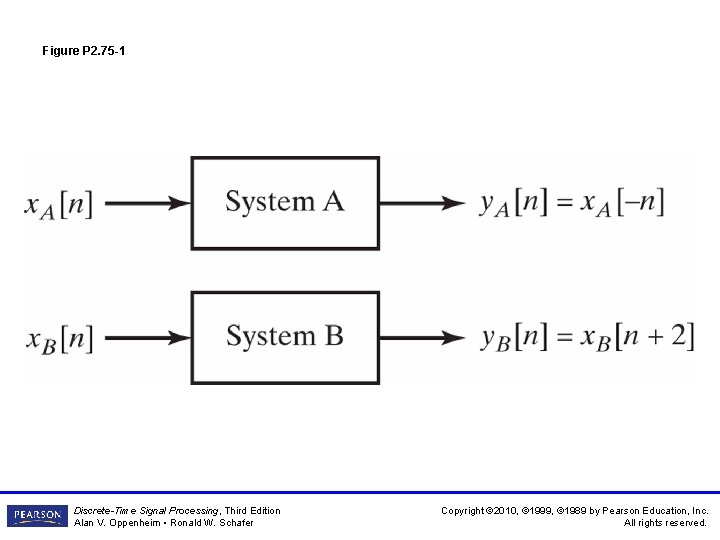
Figure P 2. 75 -1 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

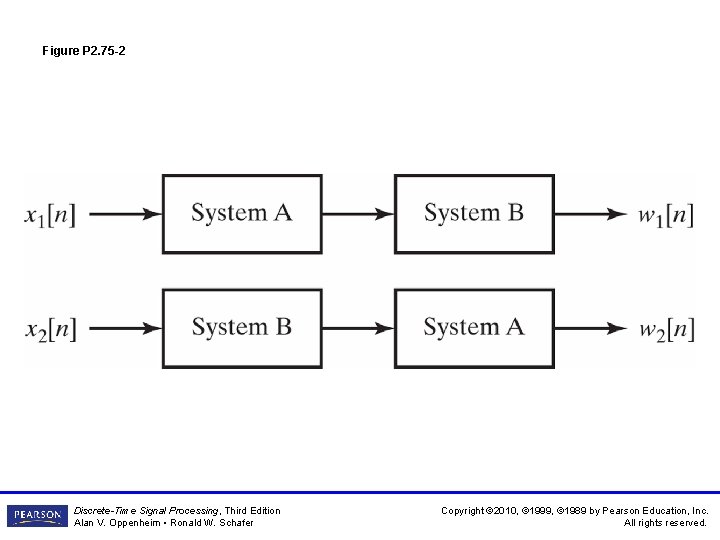
Figure P 2. 75 -2 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

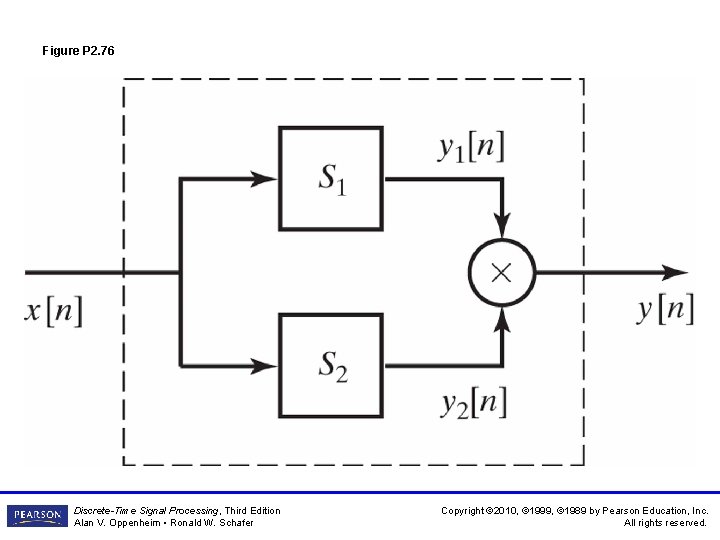
Figure P 2. 76 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

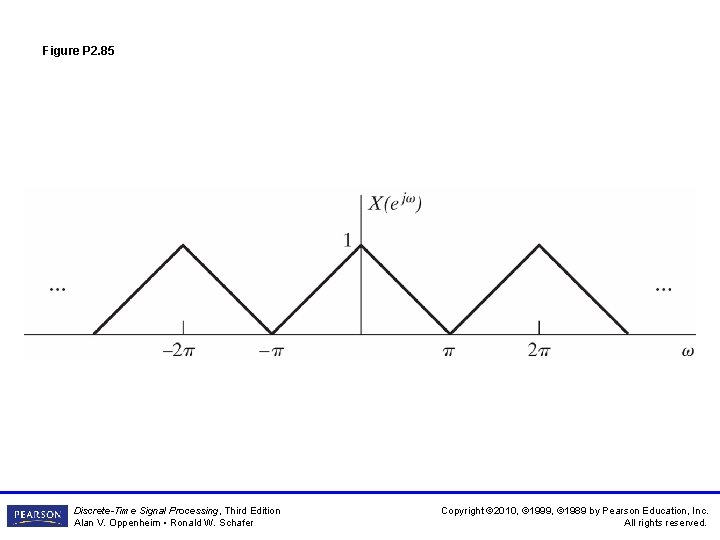
Figure P 2. 85 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

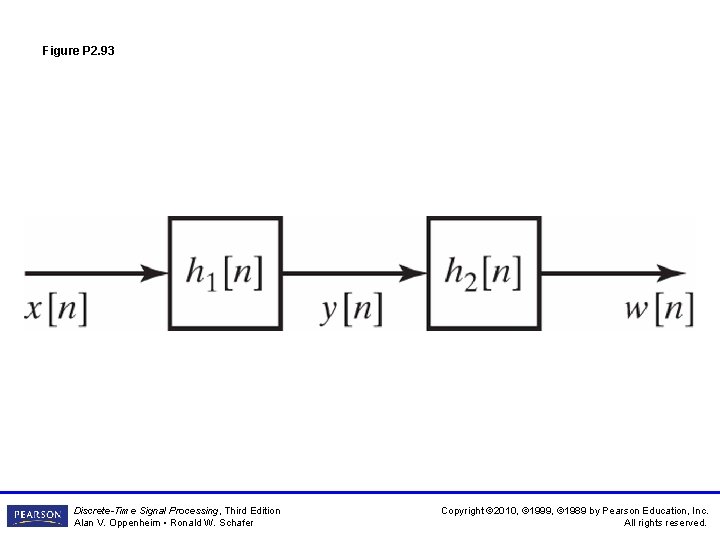
Figure P 2. 93 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

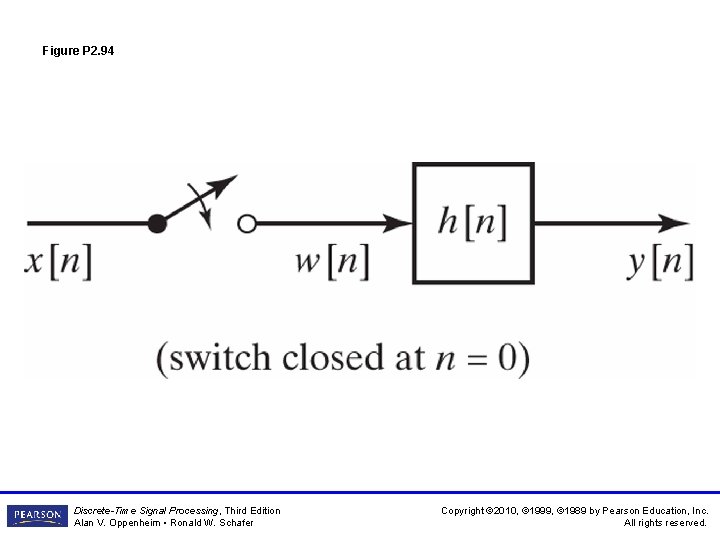
Figure P 2. 94 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

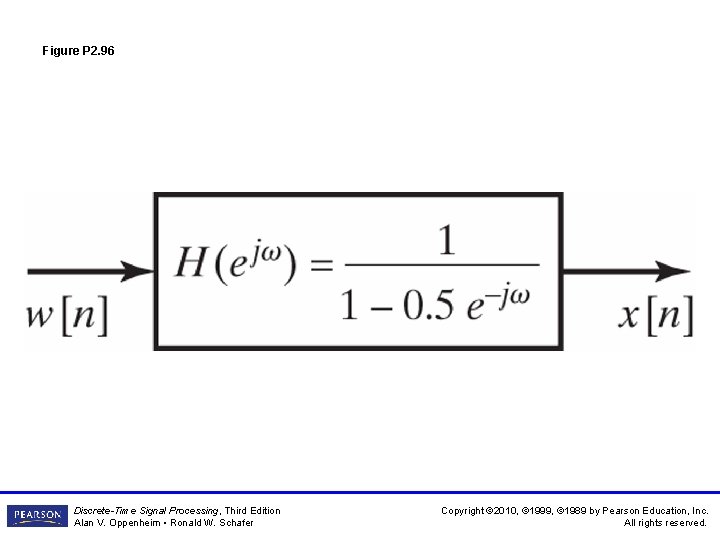
Figure P 2. 96 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

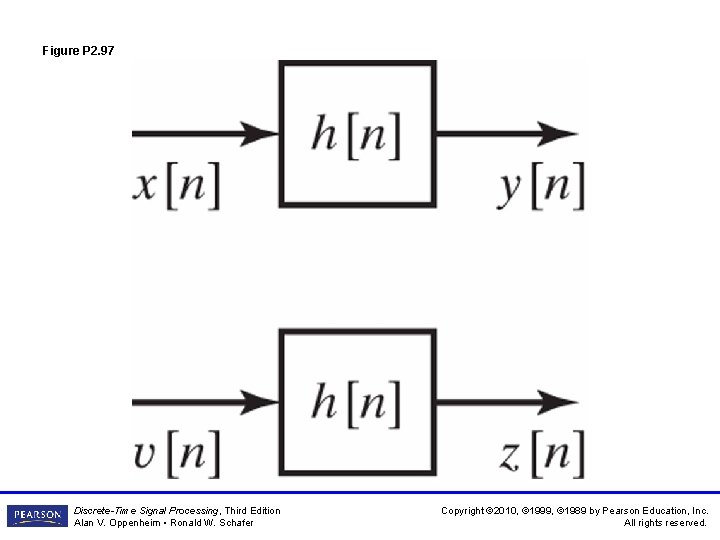
Figure P 2. 97 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.

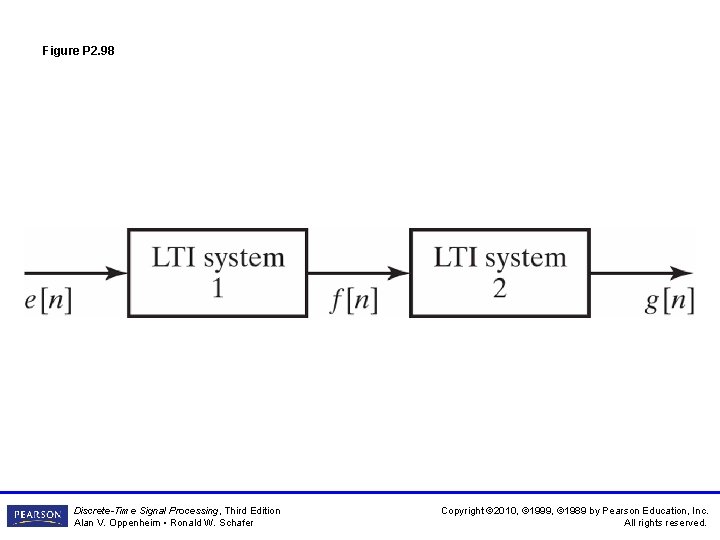
Figure P 2. 98 Discrete-Time Signal Processing, Third Edition Alan V. Oppenheim • Ronald W. Schafer Copyright © 2010, © 1999, © 1989 by Pearson Education, Inc. All rights reserved.