Fifth Grade Math State Test Review Ms Mikalauskas



















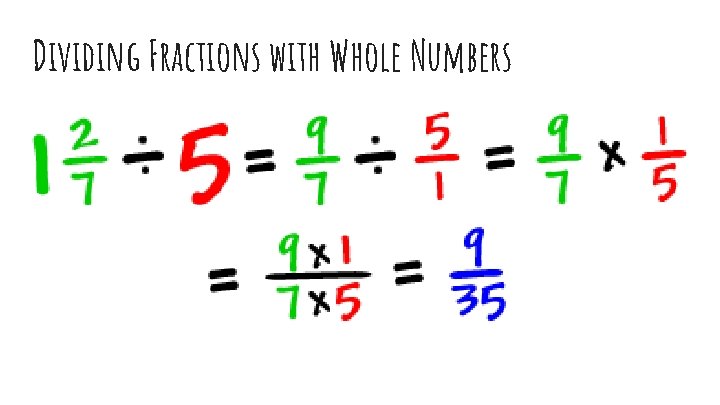




















- Slides: 53

Fifth Grade Math State Test Review Ms. Mikalauskas - St. Ann School

Topic 1: Place Value Systems Standards: 5. NBT. 1, 5. NBT. 2, 5. NBT. 3 ● ● ● Naming place value Rounding numbers according to place value Comparing numbers Expanded, word, and standard form Powers of 10

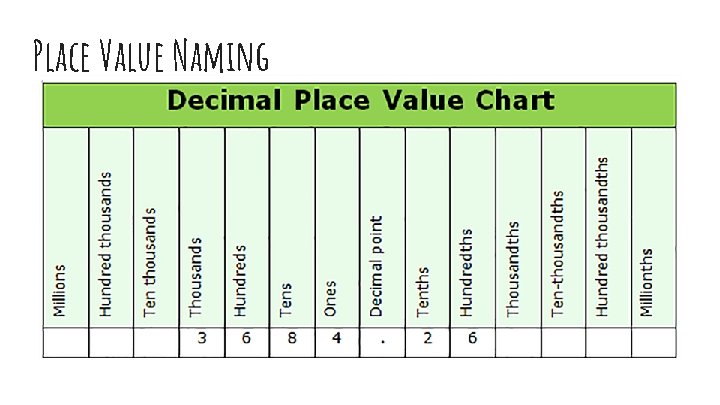
Place Value Naming

Rounding with Place value Example: Round 241. 895 to the nearest: ● ● ● Hundred : 241. 895 ○ The 4 says “leave it” = 200 Tens: 241. 895 ○ The 1 “says leave it” = 240 Ones: 241. 895 ○ The 8 “says add one more” = 242 Tenths : 241. 895 ○ The 9 “says add one more” = 241. 9 Hundredths : 241. 895 ○ The 5 “says add one more” = 241. 90

Comparing Decimals ● If the whole numbers are the same take each number one at a time to the right of the decimal. ● The number with the first larger number is bigger. ● EX: 20. 302 __>__ 20. 349 equal 0 is > 4

Word form When putting numbers in word form, write it the way it would be said out loud. Example: ● ● ● 9. 4 = Nine and four tenths 87. 49 = Eighty-seven and forty-nine hundredths 594. 236 = Five hundred ninety-four and two hundred thirty-six thousandths

Standard Form ● Standard forms is the way a number is expressed simply ● Examples ○ ○ 9. 4 1920 390. 94 1, 000

Expanded Form To put a number in expanded form: ● Take each digit and multiply it by the place value column it is in ● Put addition signs between numbers

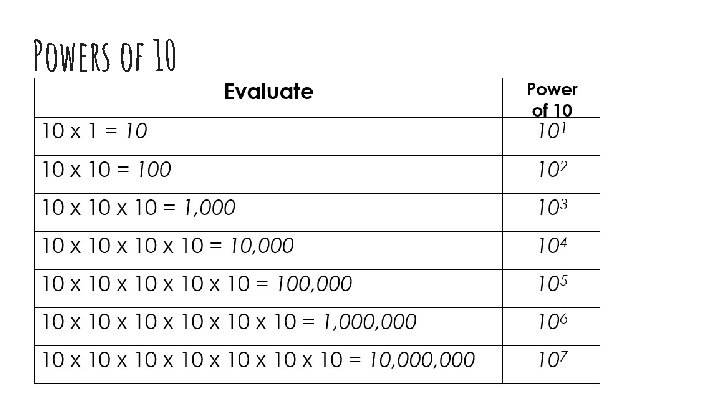
Powers of 10

Multiplying by powers of ten ● When multiplying by a power of ten move the decimal point to the right the number of times in the exponent ● Ex:

Dividing by powers of 10 ● When dividing by a power of ten move the decimal point to the LEFT the number of times in the exponent

Topic 3: Decimals Standards: 5. NBT. 4, 5. NBT. 5, 5. NBT. 6 & 5. NBT. 7 ● ● ● Adding and subtracting Multiplying Dividing Comparing Rounding

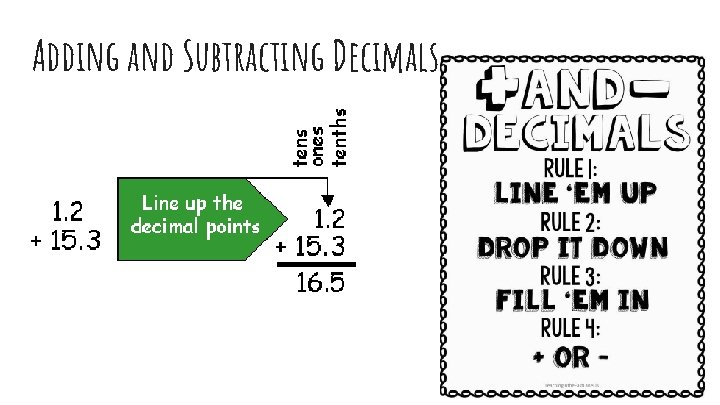
Adding and Subtracting Decimals

Multiplying Decimals

Dividing Decimals

Topic 3: Fractions Standards: 5. NF. 1 -5. NF. 7 ● ● ● ● Least Common Multiple Greatest Common Factor Adding and subtracting fractions Equivalent Fractions Multiplying Fractions Dividing Fractions Working with mixed numbers and improper fractions Simplifying fractions

Least Common Multiple ● Least common multiples are used to find the Least common denominator in order to solve fraction addition and subtraction problems

Greatest Common FActor ● GCF is used when simplifying fractions

Adding and Subtracting Fractions 3 +5 4 6 STEP 1: Find the LCD STEP 2: Stack Fractions and convert to LCD STEP 3: Add or subtract numerators ONLY STEP 4: Denominator stays the same STEP 5: Reduce Fraction Least Common Multiple: 4|4 8 12 16 20 + 1 4 3 6 1 x 3 6| 6 12 18 24 12 9 12 10 / 2 5 12 / 2 = 6 Greatest Common Factor: 10 | 1 2 5 10 12 | 1 2 3 4 6 12

Multiplying Fractions ● STEP 1: Put any whole numbers over 1 ● STEP 2: Multiply the numerators ● STEP 3: Multiply the denominators ● STEP 4: Simplify using the GCF

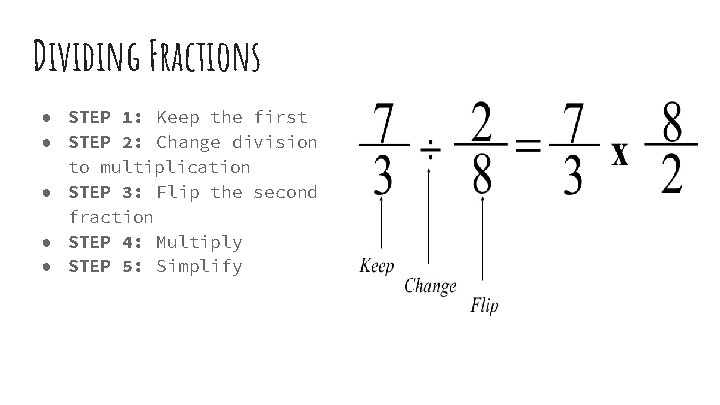
Dividing Fractions ● STEP 1: Keep the first ● STEP 2: Change division to multiplication ● STEP 3: Flip the second fraction ● STEP 4: Multiply ● STEP 5: Simplify

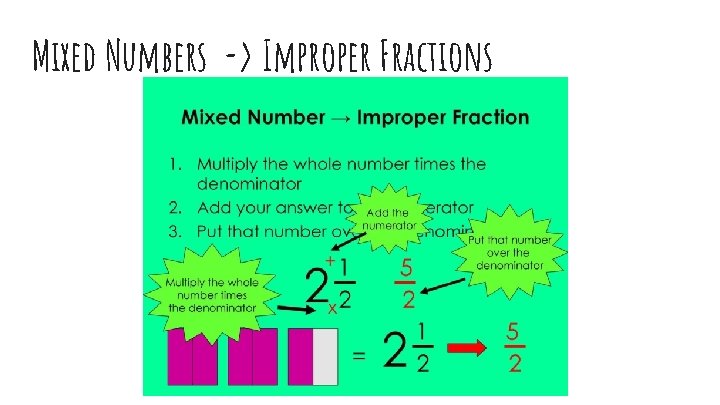
Mixed Numbers -> Improper Fractions

Improper Fractions -> Mixed Numbers

Multiplying Mixed Numbers ● STEP 1: Change Mixed numbers into improper fractions ● STEP 2: Multiply numerators and denominators ● STEP 3: Change improper fraction to mixed number ● STEP 4: Simplify
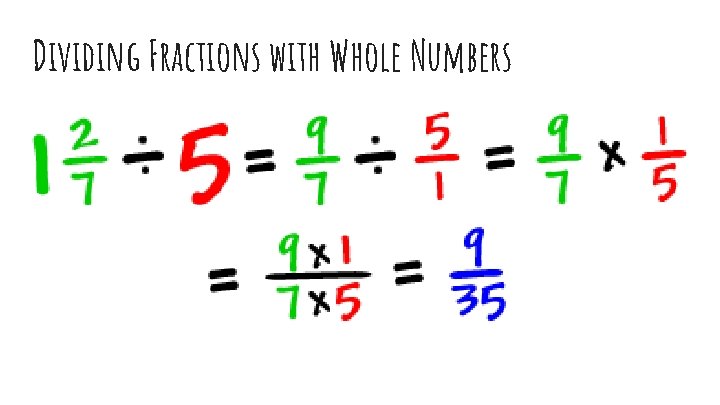
Dividing Fractions with Whole Numbers

Simplifying Fractions

Simplifying Fractions Sometimes we think we found the greatest common factor when we only found a common factor. If you get an answer that still has common factors you must keep dividing until it is in its simplest form.

Topic 5: Number Lines ● Can be used to find order of numbers ● Used when making fraction line plots ● Relates to x and y axis on a coordinate plane

Number Lines ● Not all number lines increase or decrease by intervals of one ● Follow these steps to correctly label number lines:

Integer order ● Listing numbers in least to greatest or greatest to least can be found by using a number line. ● Order from least to greatest: A, E, D, B, C ● Order from greatest to least: C, B, D, E, A

● ● ● The greatest snowfall was 6/8 Most common= 2/8 In total? Add: 1/8 + 2/8 + 5/8 + 6/8 = 31/8 = 3⅞ ● Difference between the least snowfall and the greatest? ○ Subtract 6/8 -1/8= 5/8

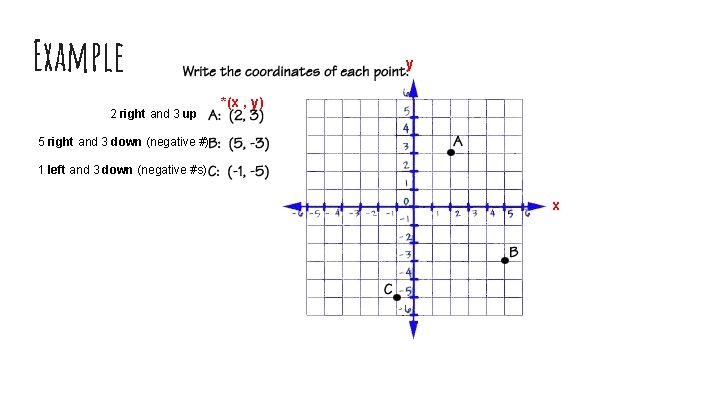
Axis ● The x-axis goes (horizontal) ● The y-axis goes (vertical) ● Coordinates are ● Start at origin left to right across the coordinate plane up and down the coordinate plane always plotted (x, y) (*alphabetical) - move along x and then move along y

Example 2 right and 3 up y *(x , y) 5 right and 3 down (negative #) 1 left and 3 down (negative #s) x

Topic 6: Measurements and Data Standards: 5. MD. 1 - 5. MD. 5 ● Volume relation to addition and subtraction ● Converting measurements within a measurement system ● Measurement conversions

Common Conversions There will be a reference sheet with some of these conversions for you. However, it does not hurt to be familiar with them.


HOW TO CONVERT When converting draw an arrow from what you have to what you are going to. The amount of columns you count is the amount of times you move your decimal. Example: 128. 5 meters converted into: 1. Centimeters (2 columns to the right of meters) - move decimal twice to the right = 128. 5 cm 2. Kilometers (3 columns to the left of meters) - move decimal three times to the left =. 1285 km Example 2: 48 centigrams 1. Kilograms (5 columns to the left of centi) - move decimal 5 times to the left =. 00048 2. Milligrams (1 column to the right of centi) - move decimal once to the right = 480 mg

Topic 7: Volume is used to describe the amount of space taken up by a 3 D object. Our answer is always expressed to the third power called “cubed” We can use cubic units to help us figure out the volume of certain objects.

The volume of the first prism would be found by: 3 x 3 = 27 cubic feet The volume of the second prism would be found by: 2 x 4 x 3 = 24 cubic feet To find the difference we must subtract 27 -24= 3

Topic 8: Operations ● Operations are used to interpret numerical expressions ● We must be able to identify when the correct operation should be used ● Interpret numerical expressions ● Analyze patterns and relationships

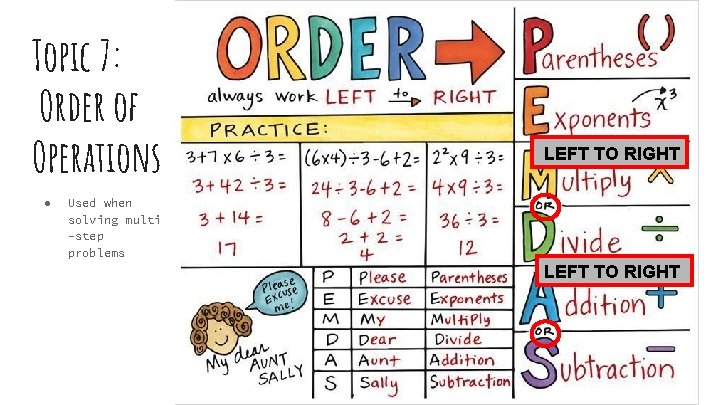
Topic 7: Order of Operations ● LEFT TO RIGHT Used when solving multi -step problems LEFT TO RIGHT

Associative Property Addition: Parenthesis can move without affecting the outcome of your problem Multiplication: Parenthesis can move without affecting the outcome of your problem

Distributive Property

Commutative Property ● The order may change when only one operation is present and the outcome will not change.


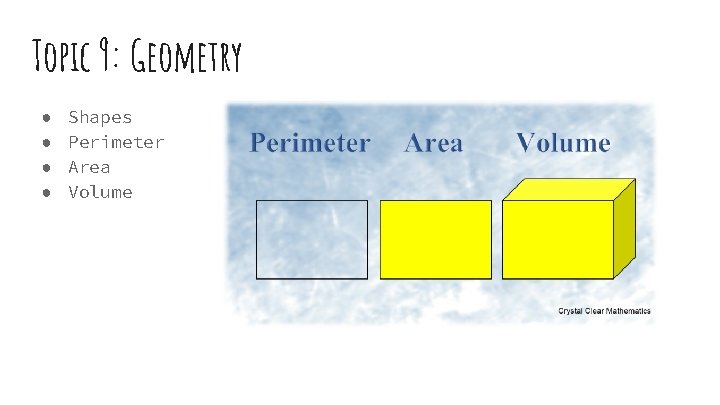
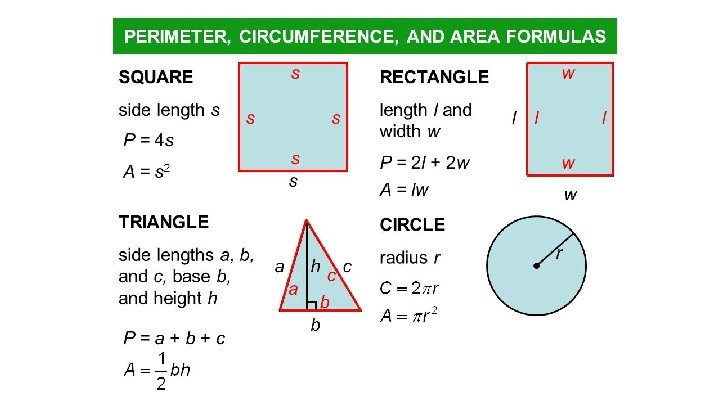
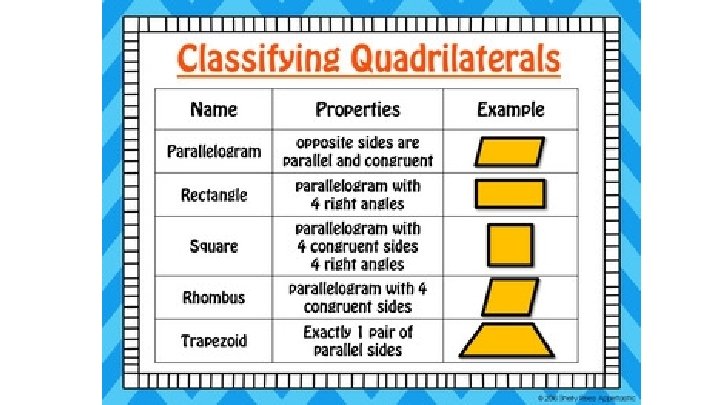
Topic 9: Geometry ● ● Shapes Perimeter Area Volume

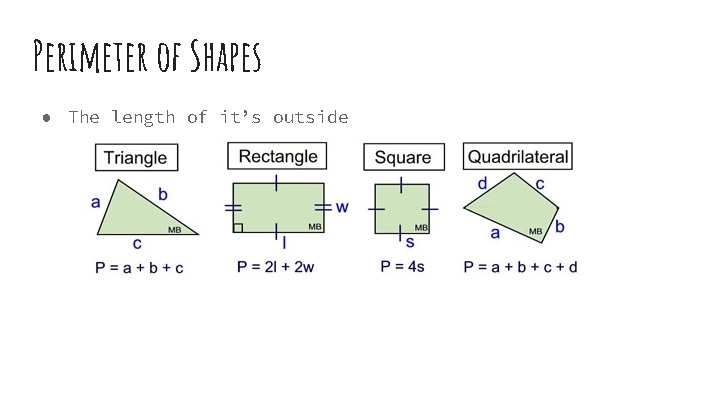
Perimeter of Shapes ● The length of it’s outside

Area of A Rectangle

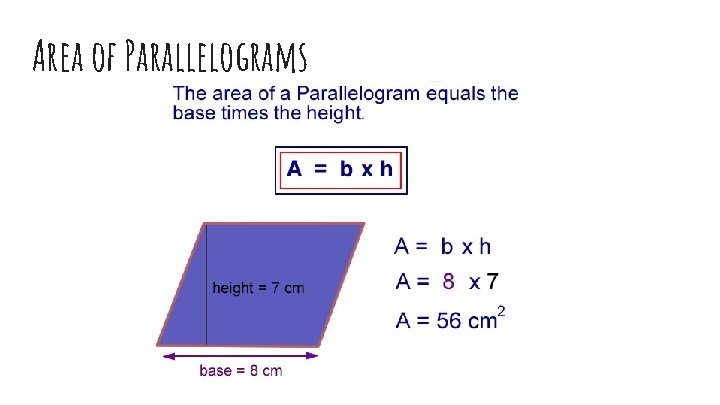
Area of Parallelograms

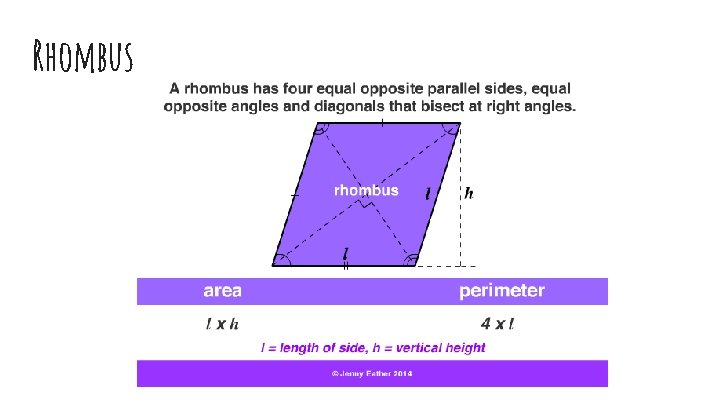
Rhombus


