Field Theory Gravity Take 2 Gravitation Gravitation Austin

Gravitation Austin has a mass of 50 kg while Kevin has a mass of

Gravitational Field The Earth has a mass of 5. 98 x 1024 kg, and

Gravitational Field Visualizing Fields http: //www. falstad. com/vector 3 d/

Gravitational Potential Energy Assumed a uniform force Force is the negative SLOPE of Potential

Gravitational Potential Energy Some Gravity Wells

Gravitational Potential Energy Nick has a mass of 50 kg while Andrew has a

Escape Velocity/ Potential The mass of the sun is approximately 2 e 30 kg.

Escape Velocity/ Potential A 1, 000 kg satellite orbits the Earth at a distance

Coulomb’s Law A hydrogen atom consists of a proton (q= 1. 6 x 10

Electric Fields Exploring Electric Fields

Electric Fields At which point on the diagram to the right is the electric

Electric Potential Energy A fixed charge of +2 n. C rests at the origin.

Electric Potential Given the diagram above, determine in what region the electric field would

Slides: 68

Download presentation

Field Theory

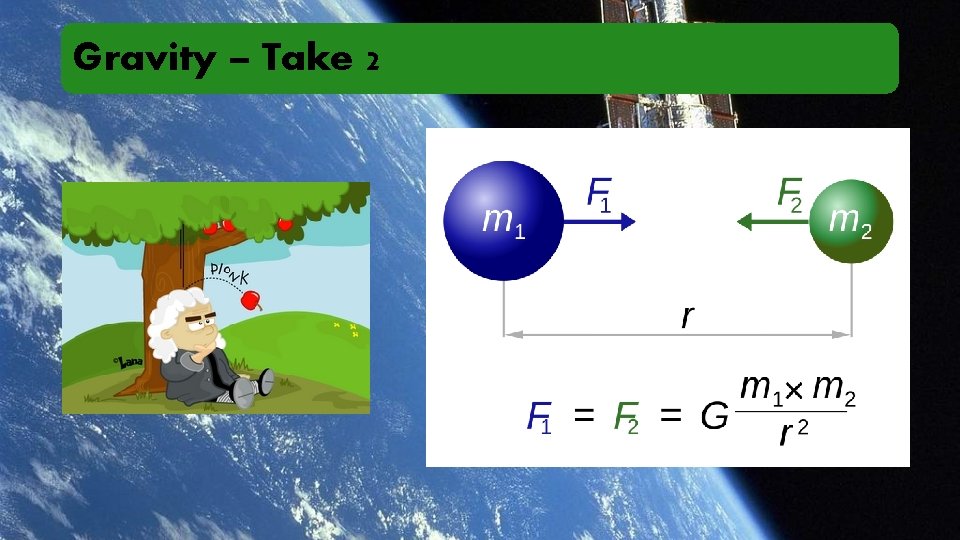
Gravity – Take 2

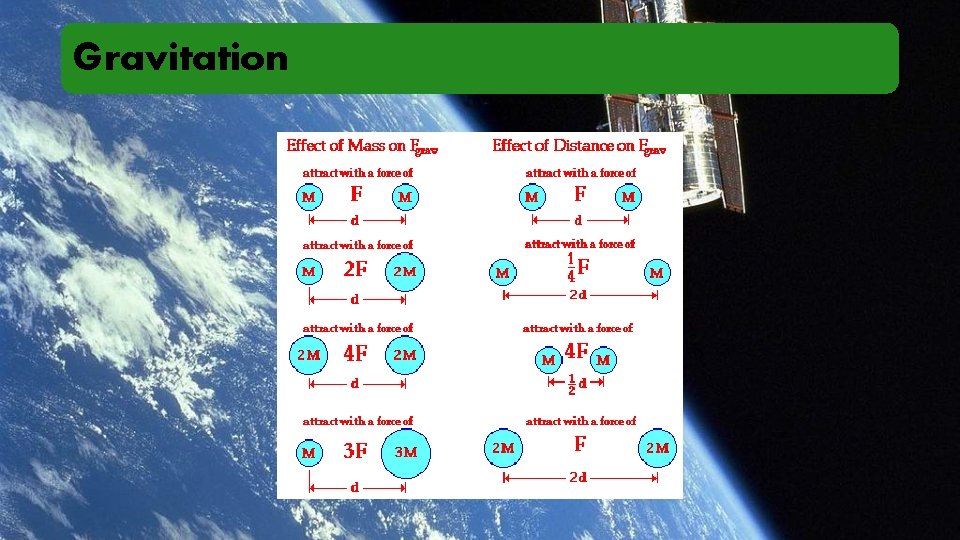
Gravitation

Gravitation Austin has a mass of 50 kg while Kevin has a mass of 60 kg. Sitting a meter apart, they notice they are attracted to each other (gravitationally). • What force does each experience? Which is greater? • In a frictionless world, what acceleration would each experience? Which is greater? Clark (100 kg) accidentally falls out of a building. As expected he accelerates downwards at a rate of 9. 8 ms-2. However, knowing that the radius of Earth is approximately 6, 300 km, his nerdy mind calculates the mass of the Earth and the acceleration of the Earth up to meet him. What are his results?

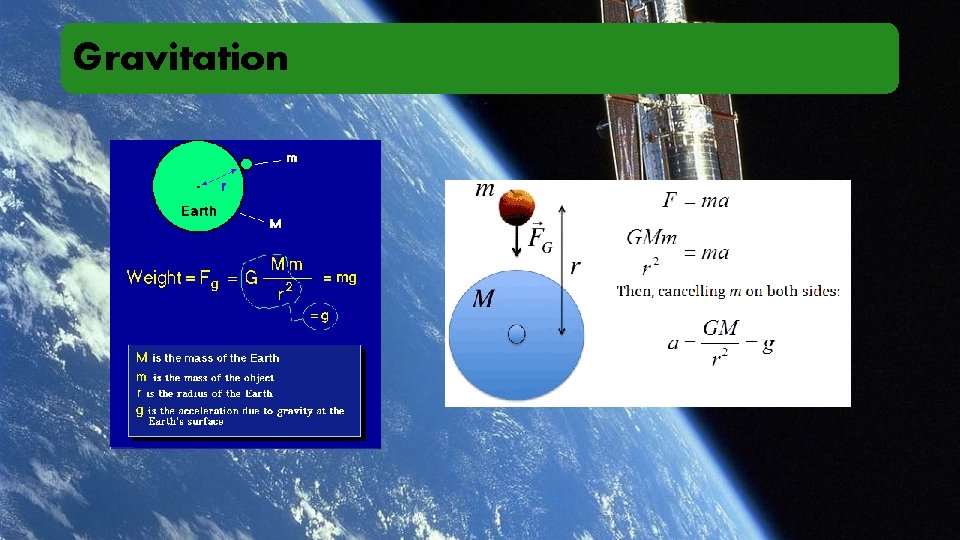
Gravitation

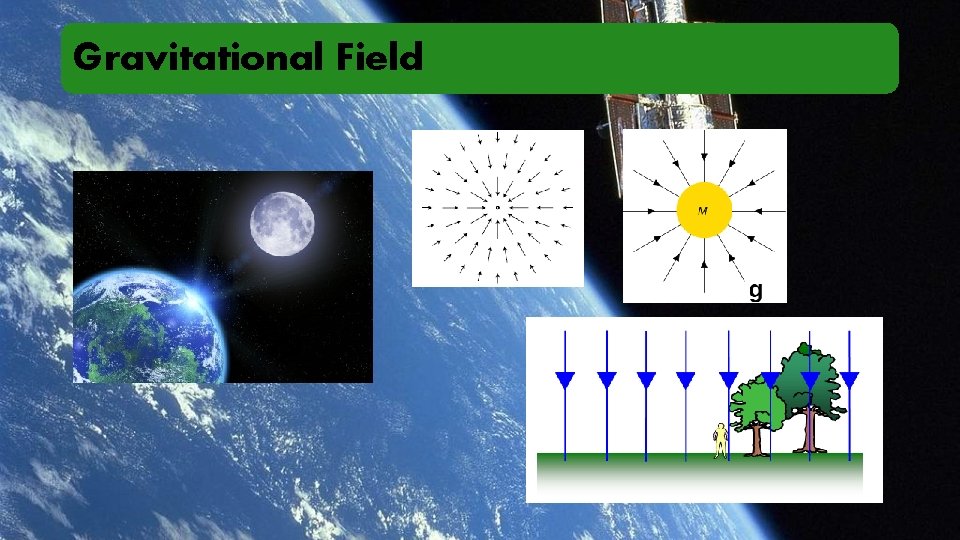
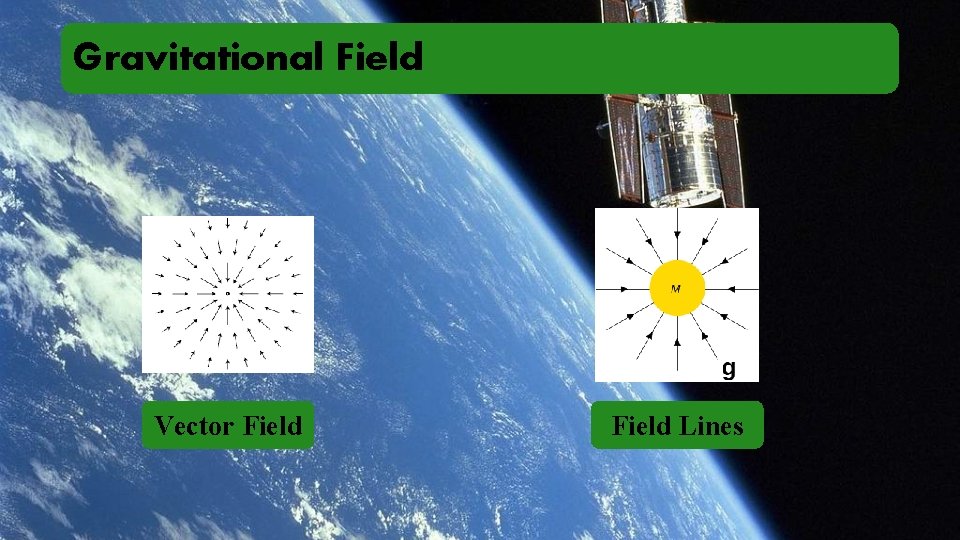
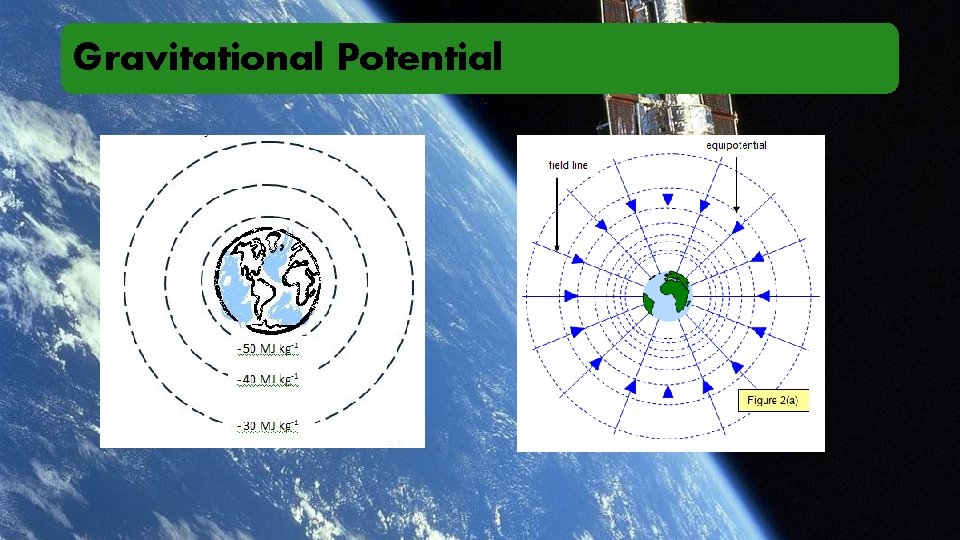
Gravitational Field

Gravitational Field Vector Field Lines

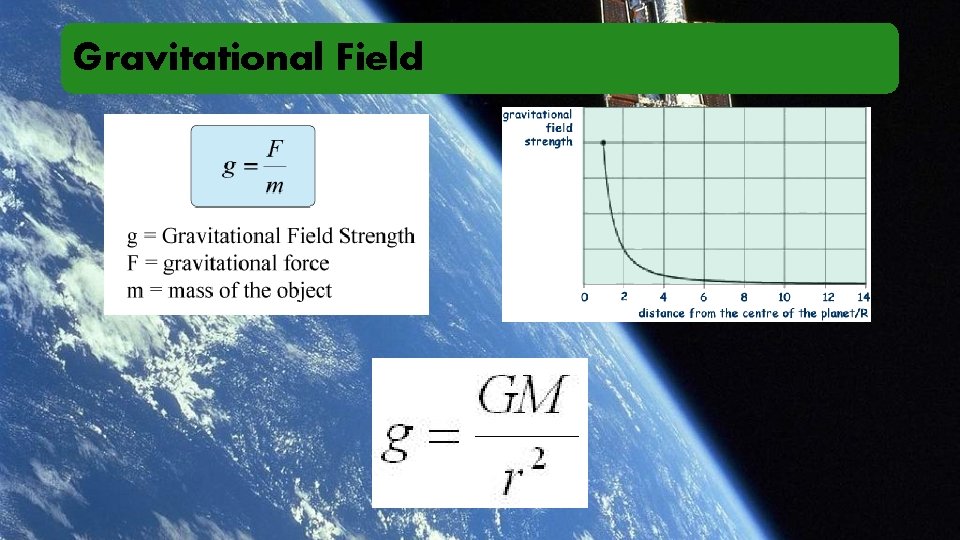
Gravitational Field

Gravitational Field The Earth has a mass of 5. 98 x 1024 kg, and an approximate radius of 6. 37 x 106 m. Determine: The gravitational field due to Earth on its surface. The gravitational field due to Earth on a satellite 35, 786 km above the surface. The gravitational field due to Earth on the Moon’s surface 384 Mm away

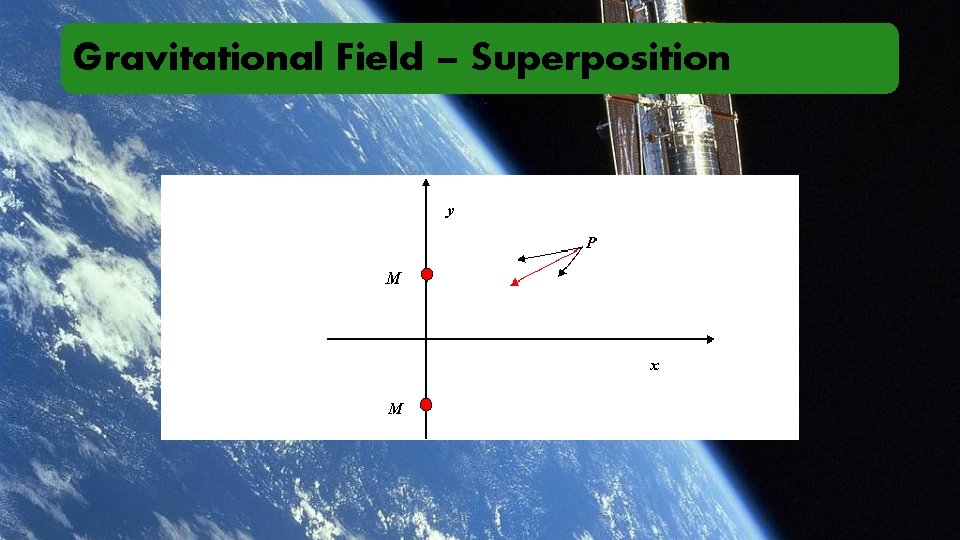
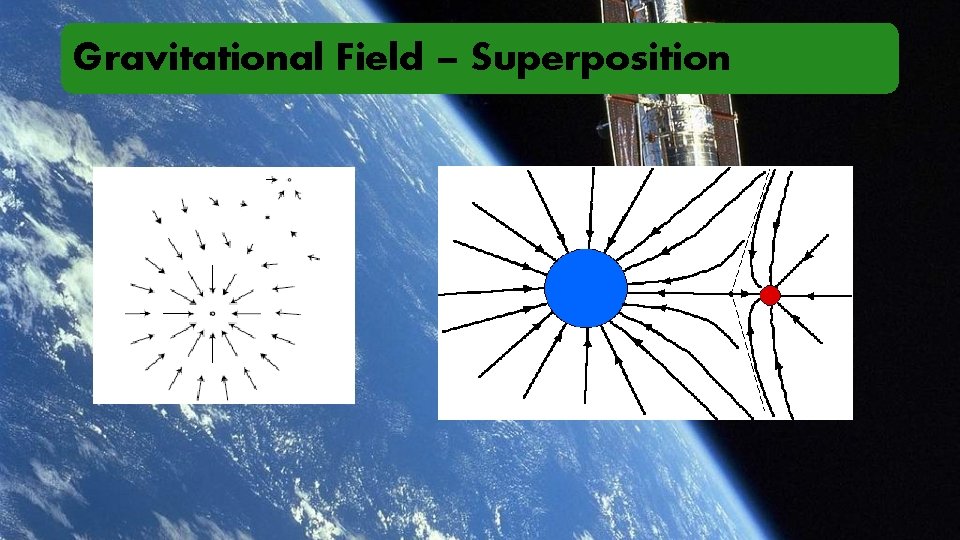
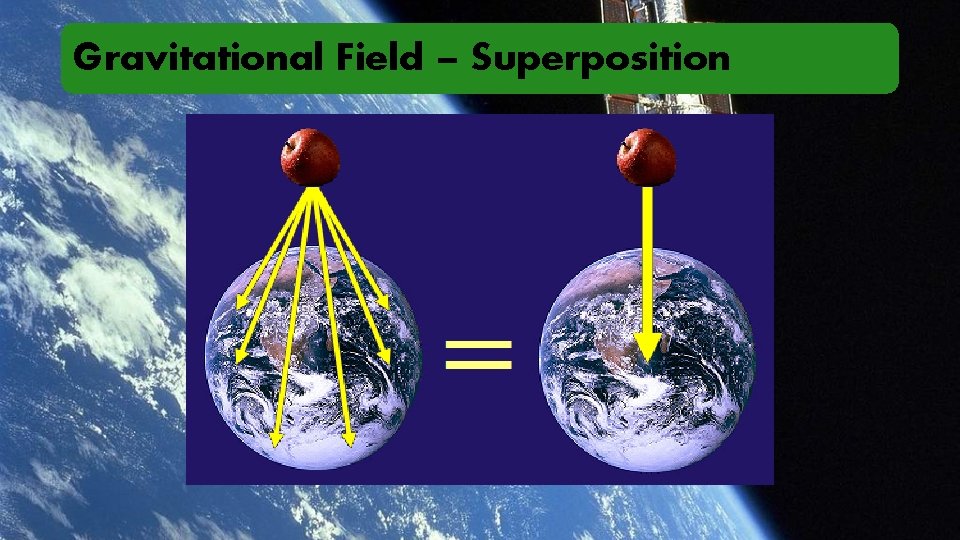
Gravitational Field – Superposition

Gravitational Field Visualizing Fields http: //www. falstad. com/vector 3 d/

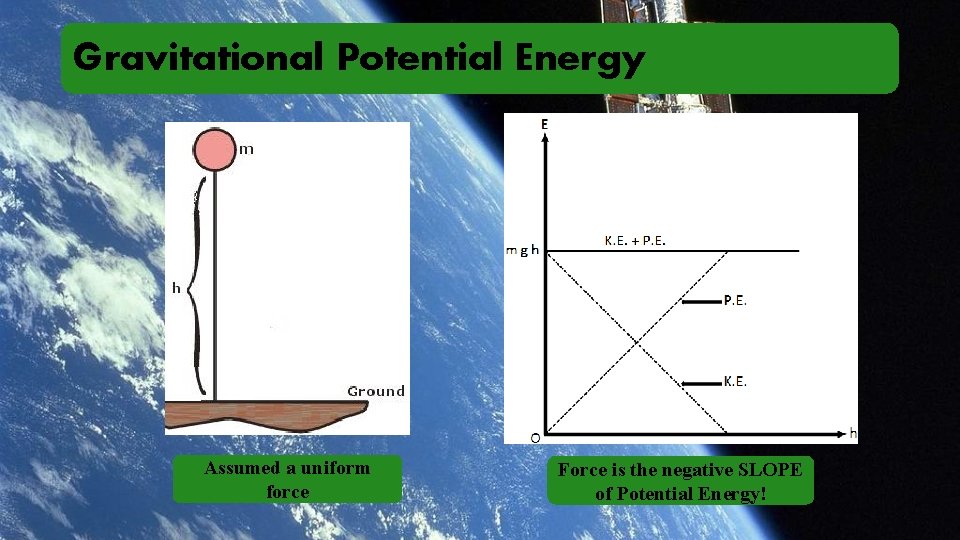
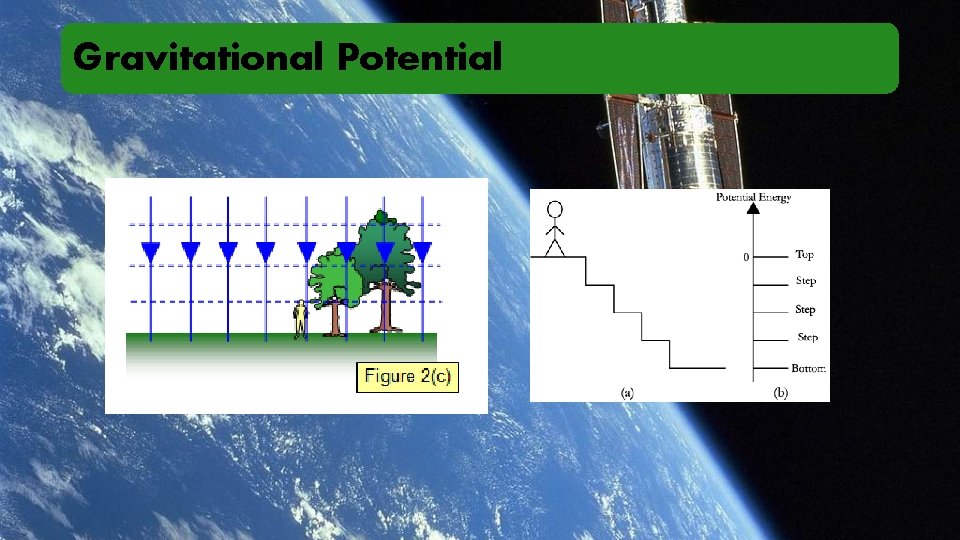
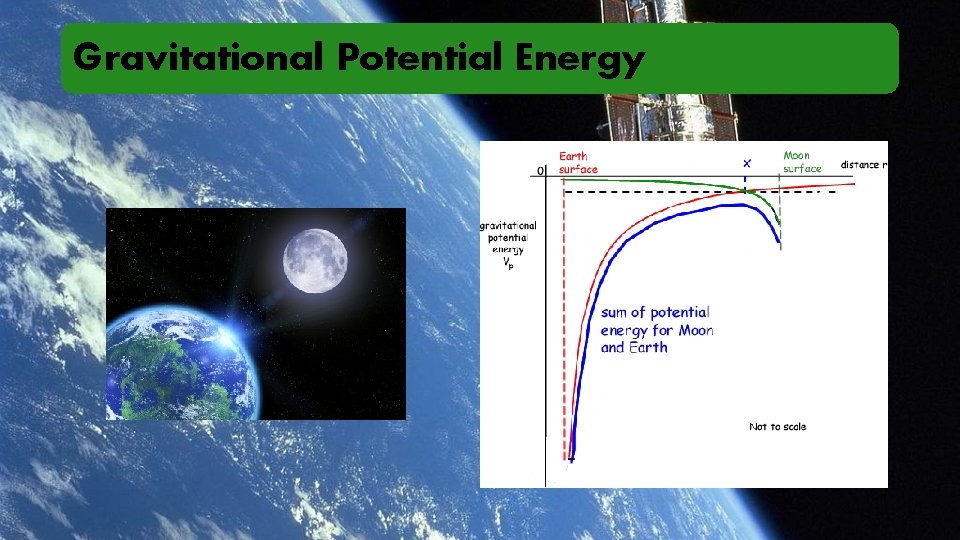
Gravitational Potential Energy Assumed a uniform force Force is the negative SLOPE of Potential Energy!

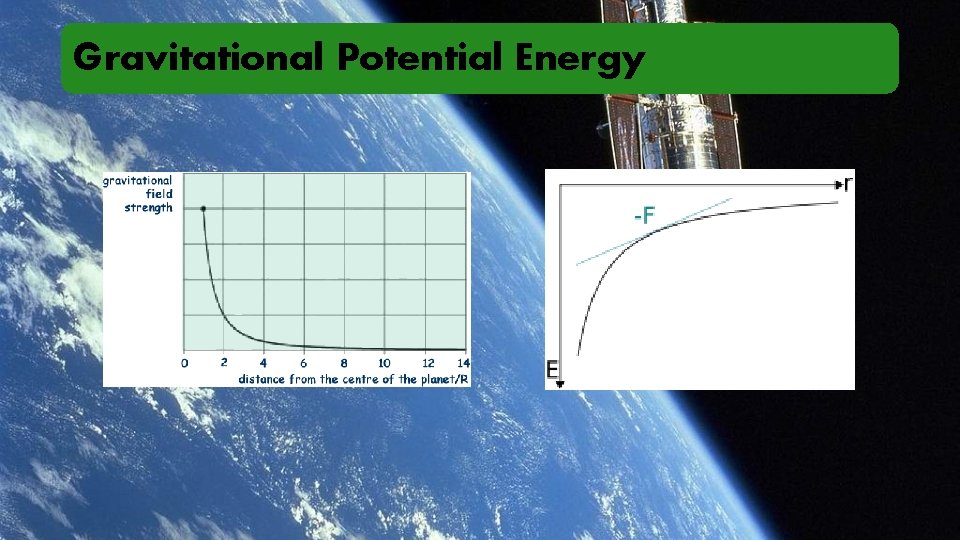
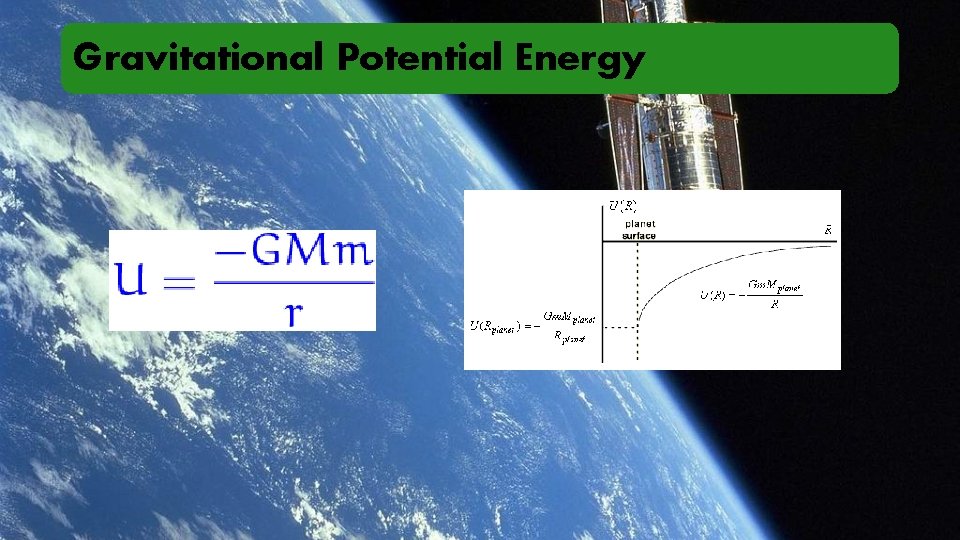
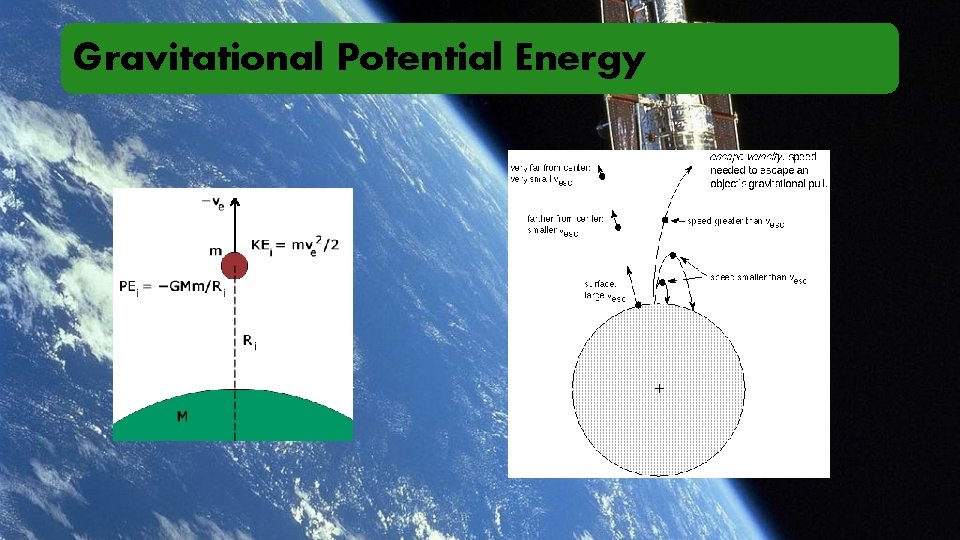
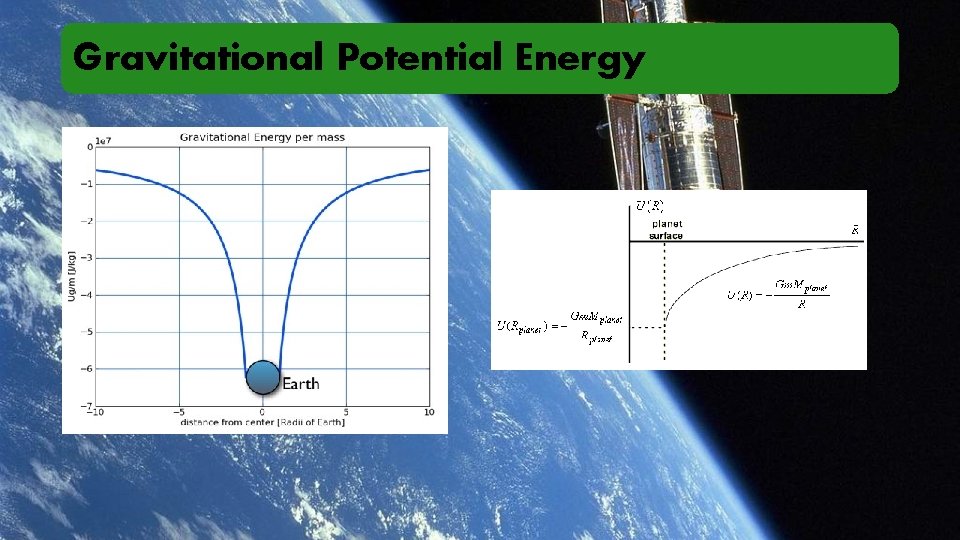
Gravitational Potential Energy

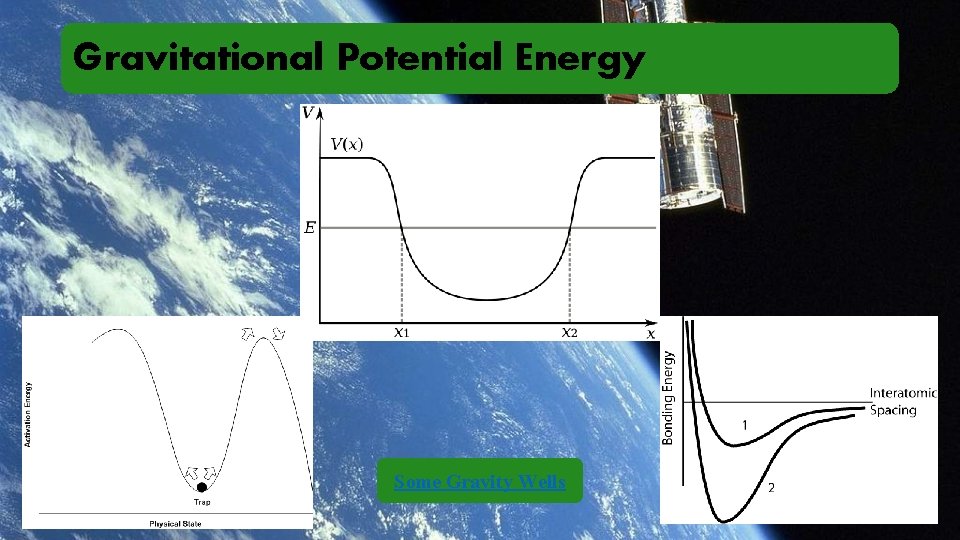
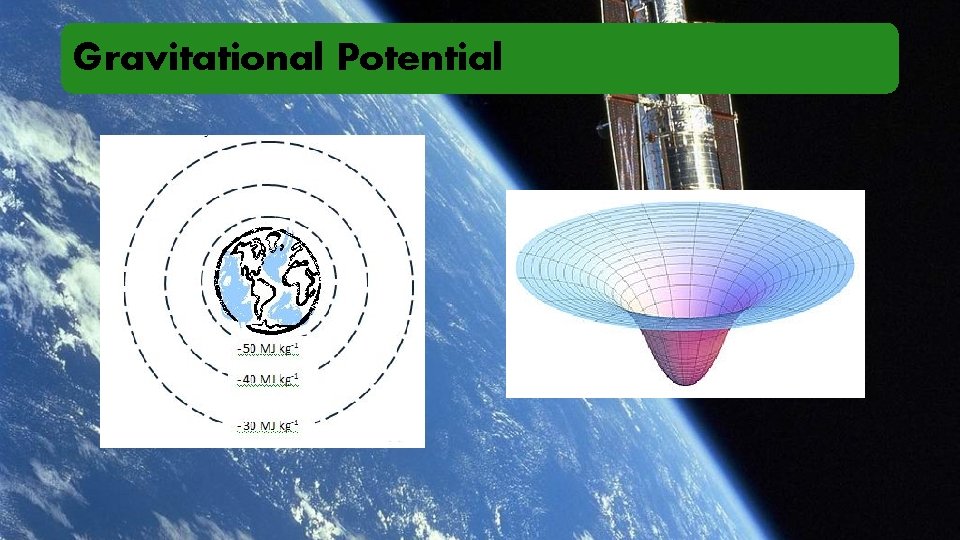
Gravitational Potential Energy Some Gravity Wells

Gravitational Potential Energy Nick has a mass of 50 kg while Andrew has a mass of 60 kg. Sitting a meter apart, they notice they are attracted to each other (gravitationally). • How much potential energy is stored between them? • How much energy needs to be added to allow them to be free from each other? Does it matter which one receives the energy? A rocket containing the world’s cats is shot from the Earth’s surface towards the sun. The Earth has a radius of 6, 370 km and a mass of 5. 98 x 1024 kg. What does the rocket’s velocity need to be to reach the sun and immolate the world’s cat supply.

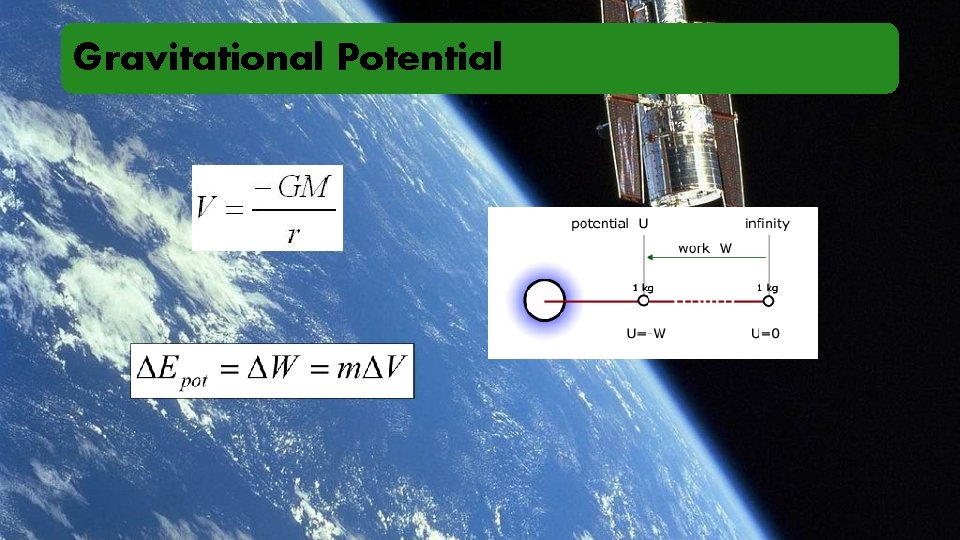
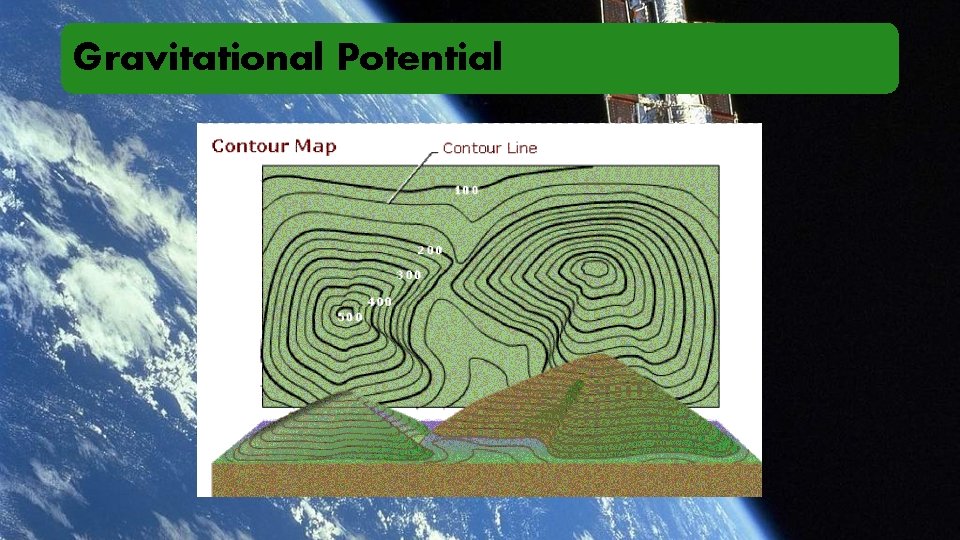
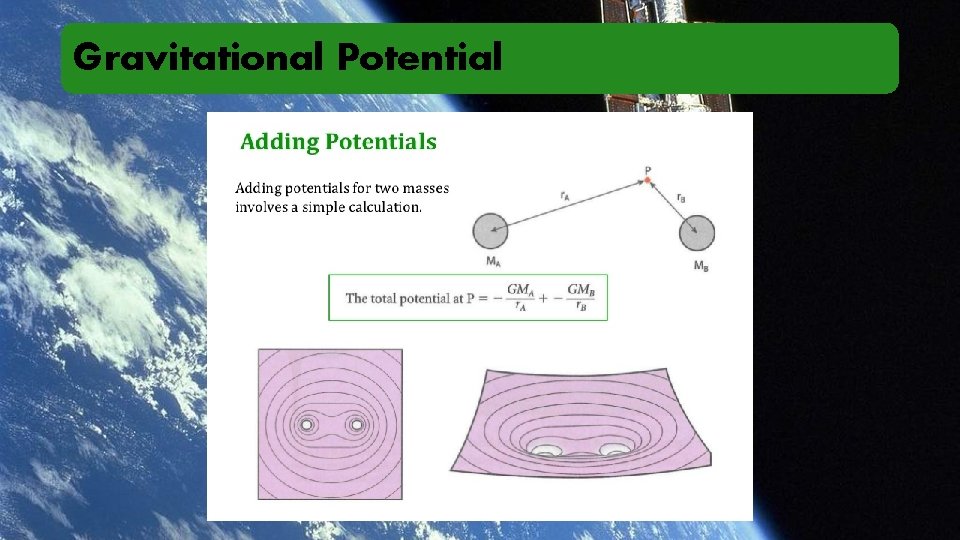
Gravitational Potential

Gravitational Potential Energy

Gravity – Take 2

Gravitational Potential

Escape Velocity/ Potential The mass of the sun is approximately 2 e 30 kg. • Determine the gravitational potential due to the sun at the Earth’s position 1. 5 e 11 m away. • Determine the gravitational potential 2. 28 e 11 m away from the Sun, where Mars is located. • Determine the amount of work needed to move a 250 kg cat from Earth to Mars (solely due to the Sun’s potential). The Earth (5. 98 e 24 kg) and the Moon (7. 35 e 22 kg) are separated by a distance of 384 Mm. Determine: • The net gravitational field mid-way between the moon and Earth. • The net gravitational potential mid-way between the moon and Earth.

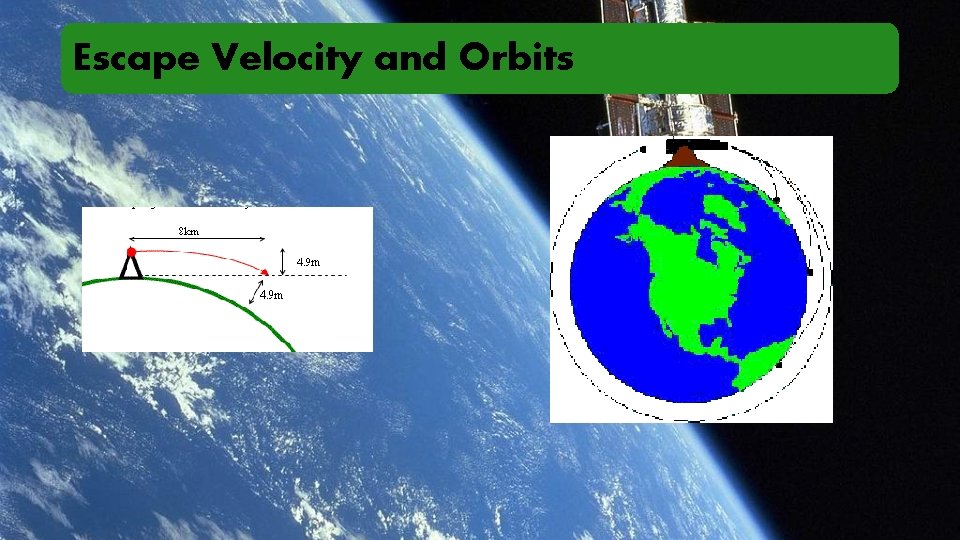
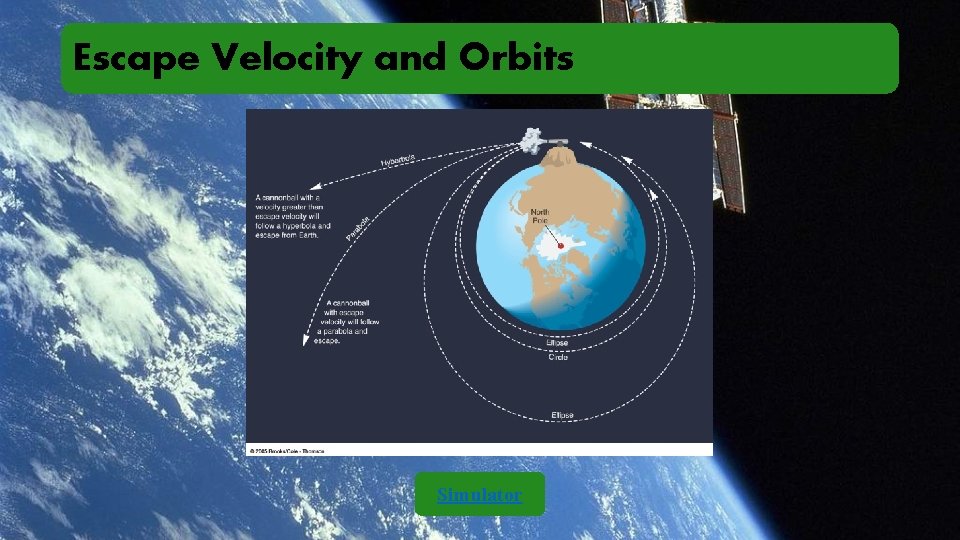
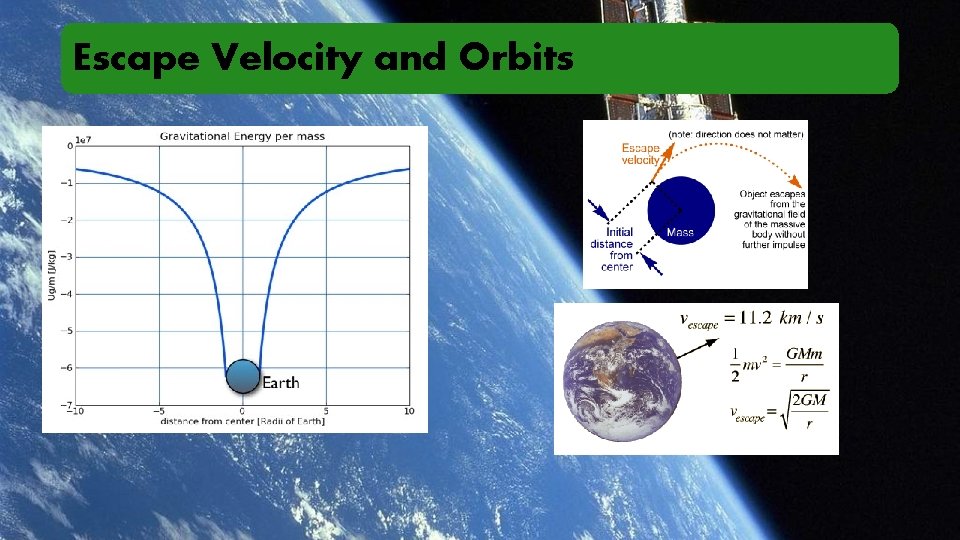
Escape Velocity and Orbits

Escape Velocity and Orbits Simulator

Escape Velocity and Orbits

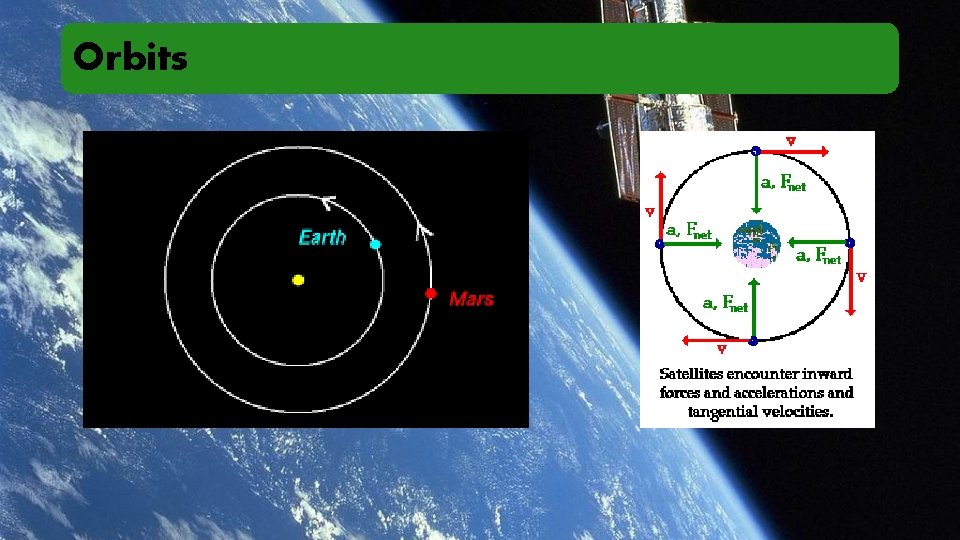
Orbits

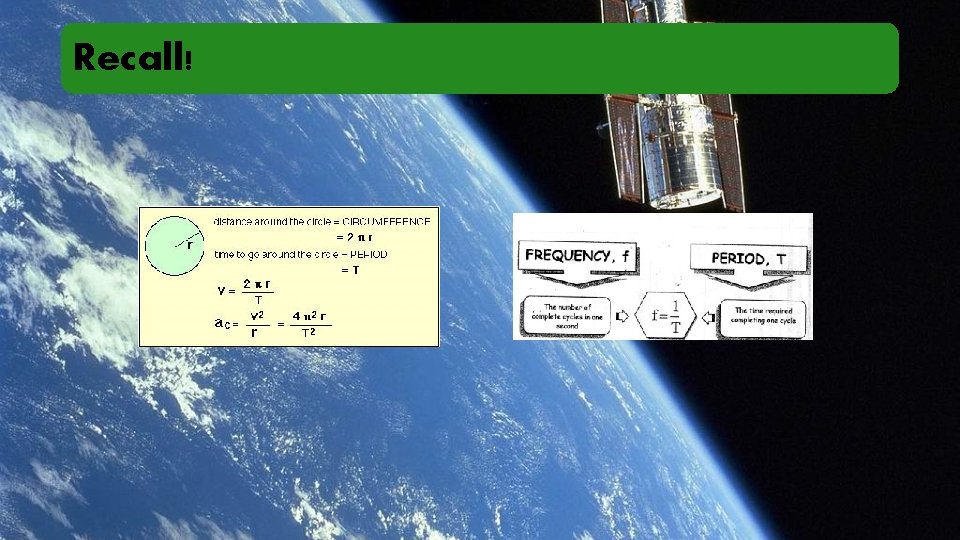
Recall!

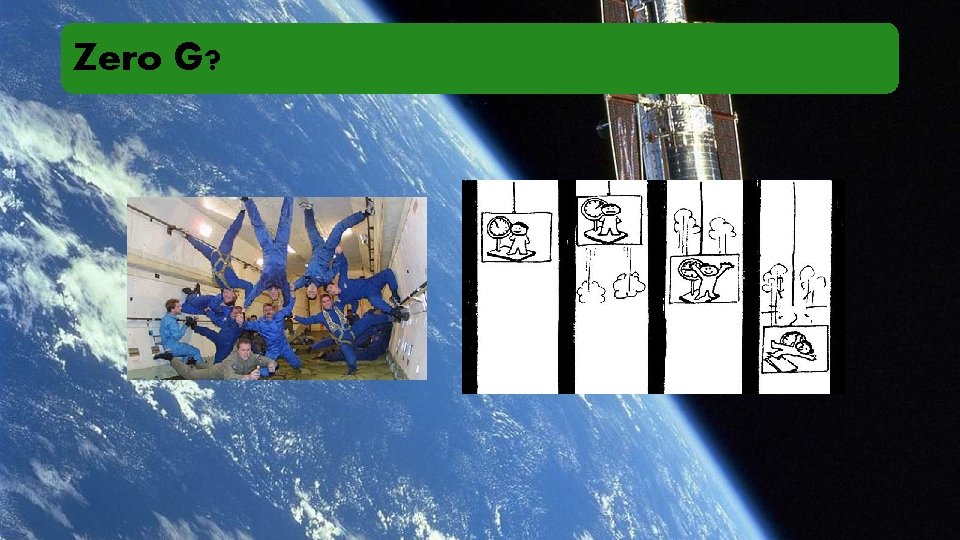
Zero G?

Escape Velocity/ Potential A 1, 000 kg satellite orbits the Earth at a distance of 1, 000 km above the surface. • What is the gravitational field due to Earth at the satellite’s location? • What is the gravitational force on the satellite? • What is the acceleration of the satellite? • What is the velocity of the satellite? • What is the period of and frequency of the satellite’s orbit? • What is the potential energy of the satellite? (HL) • What is the kinetic energy of the satellite? (HL) • What is the total energy of the satellite? (HL)

Checkpoint

Electric Charge

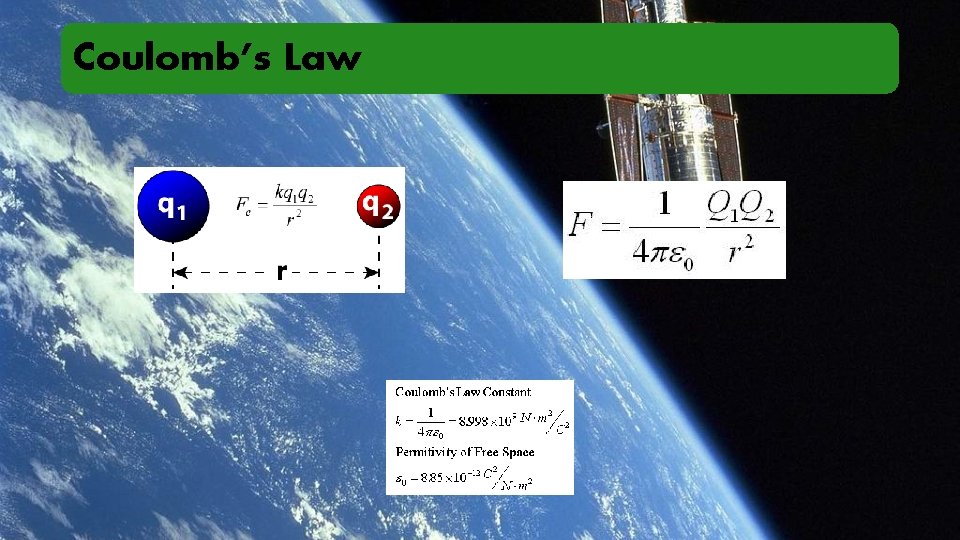
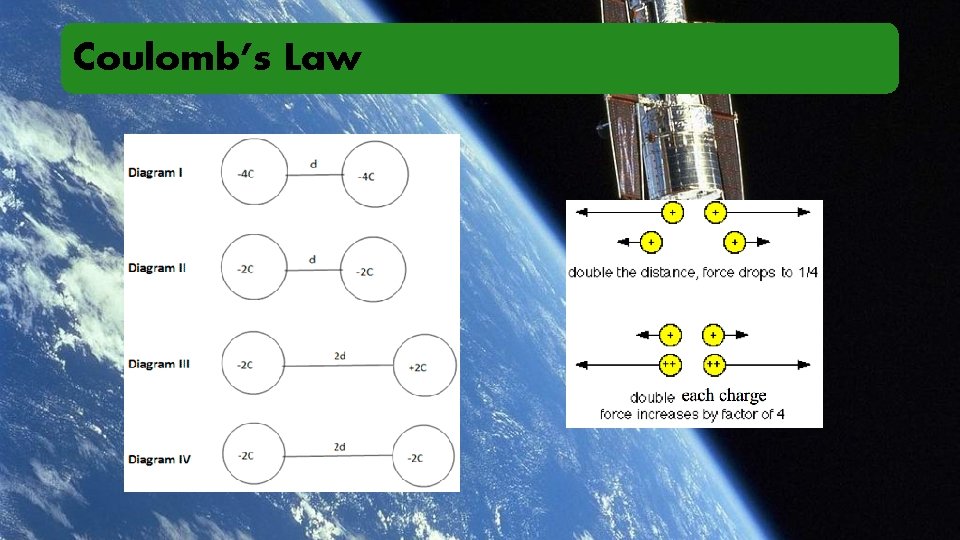
Coulomb’s Law

Coulomb’s Law A hydrogen atom consists of a proton (q= 1. 6 x 10 -19 C, m= 1. 67 x 10 -27 kg) being orbited by an electron (q= -1. 6 x 10 -19 C, m= 9. 11 x 10 -31 kg) at a radius of 0. 529 x 10 -10 m. • Determine the electric force of attraction between the proton and electron. • How many times greater is the electric attraction than the gravitational attraction? • How fast is the electron moving? • Determine the frequency of the electron’s rotation.

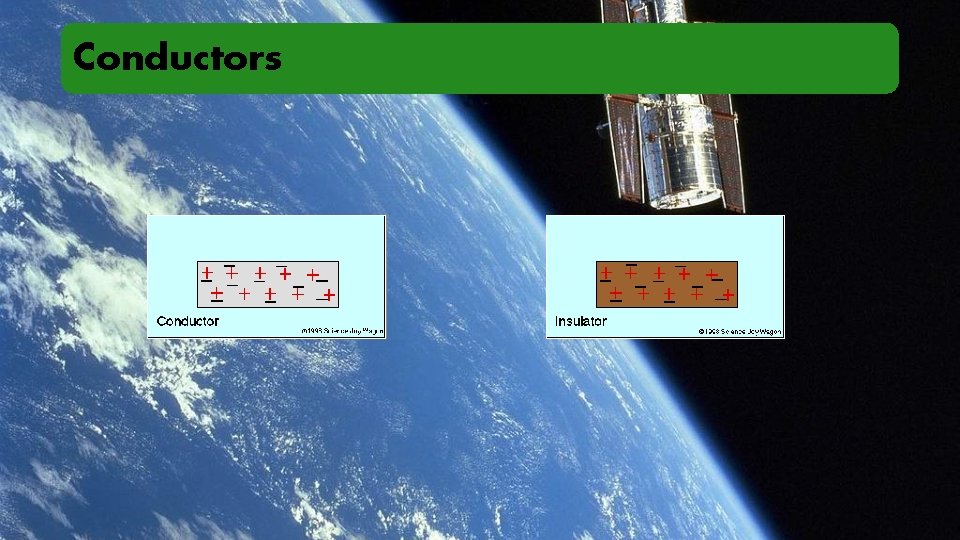
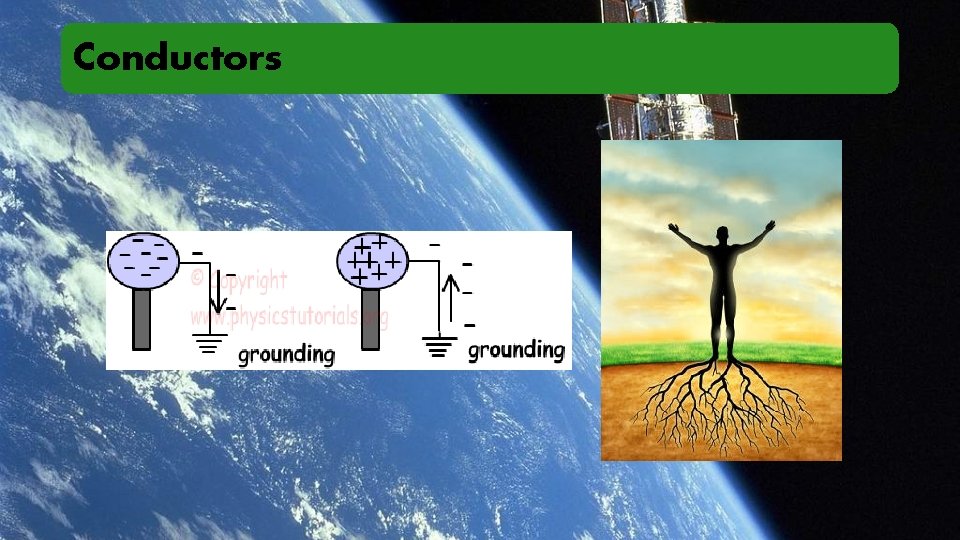
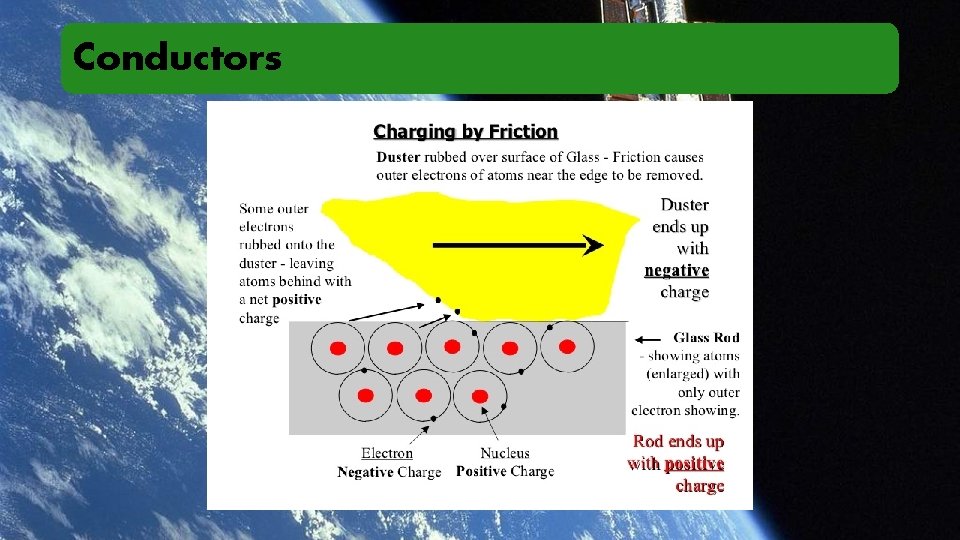
Conductors

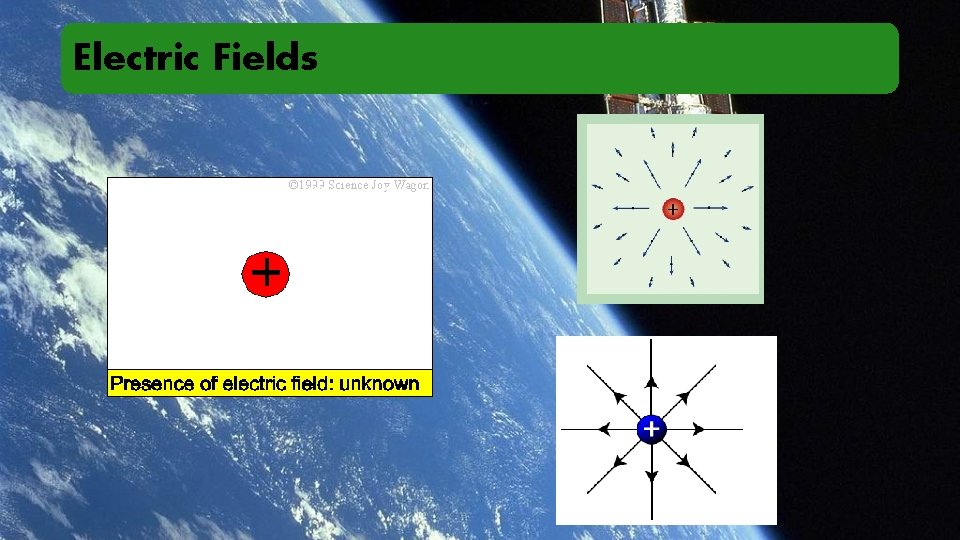
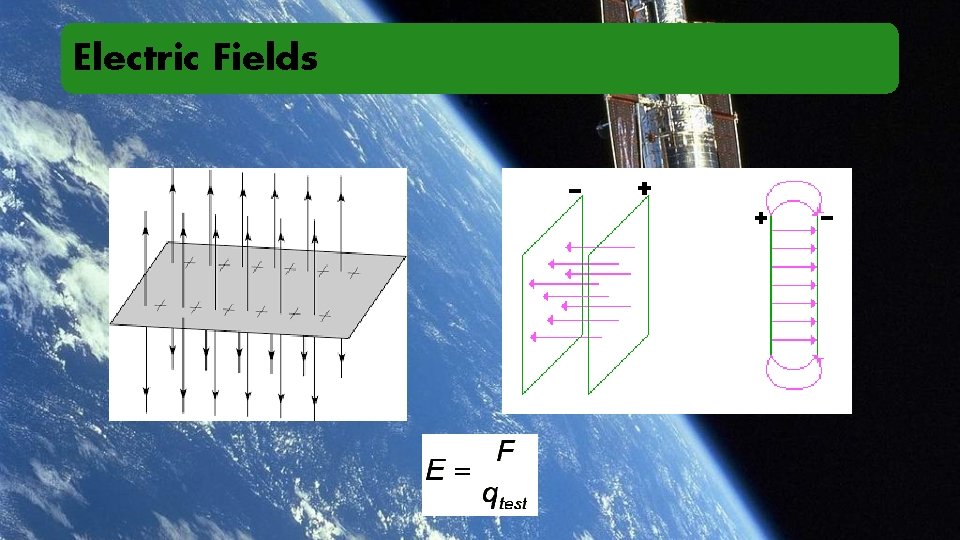
Electric Fields

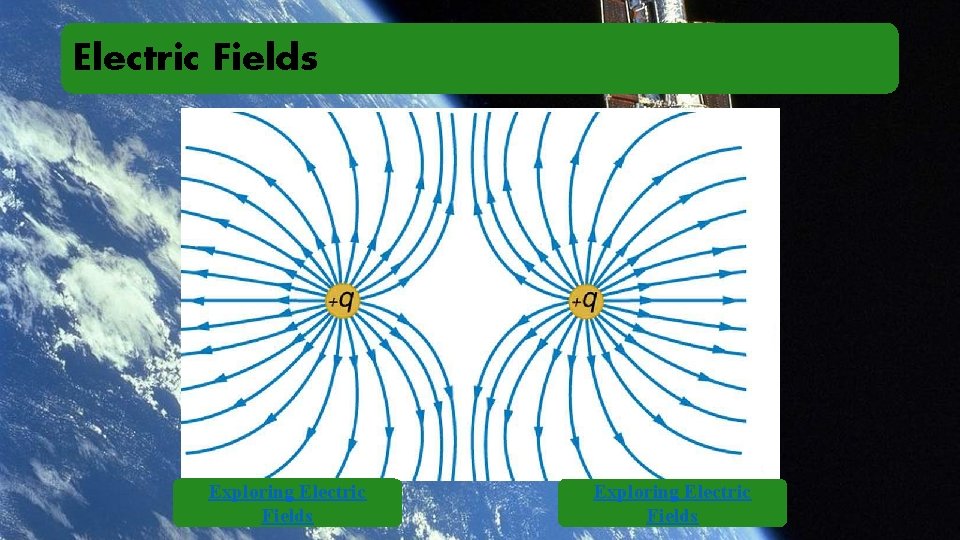
Electric Fields Exploring Electric Fields

Electric Fields

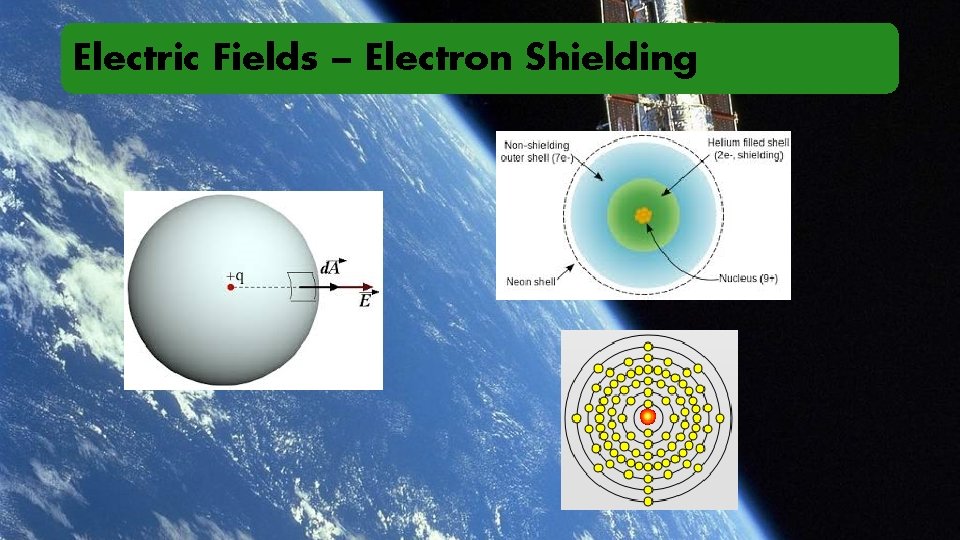
Electric Fields – Electron Shielding

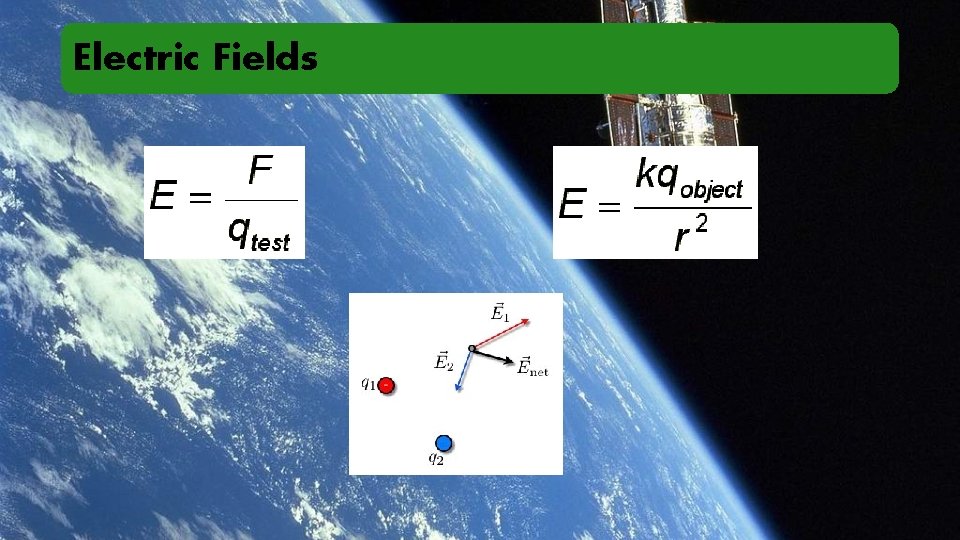
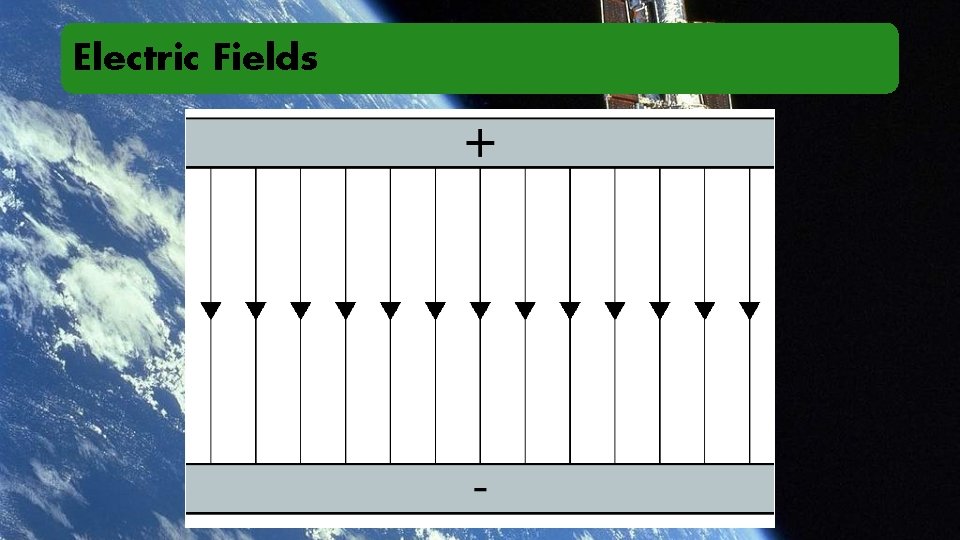
Electric Fields

Electric Fields At which point on the diagram to the right is the electric field zero? An electron is shot into a uniform electric field with a strength of 400 N/C as shown. The length of the field is 2 m and the initial velocity of the electron is 1 km/s. Determine: • The force on the electron. • The acceleration of the electron. • The vertical displacement of the electron when it exits the chamber. • The final velocity of the electron as it exits.

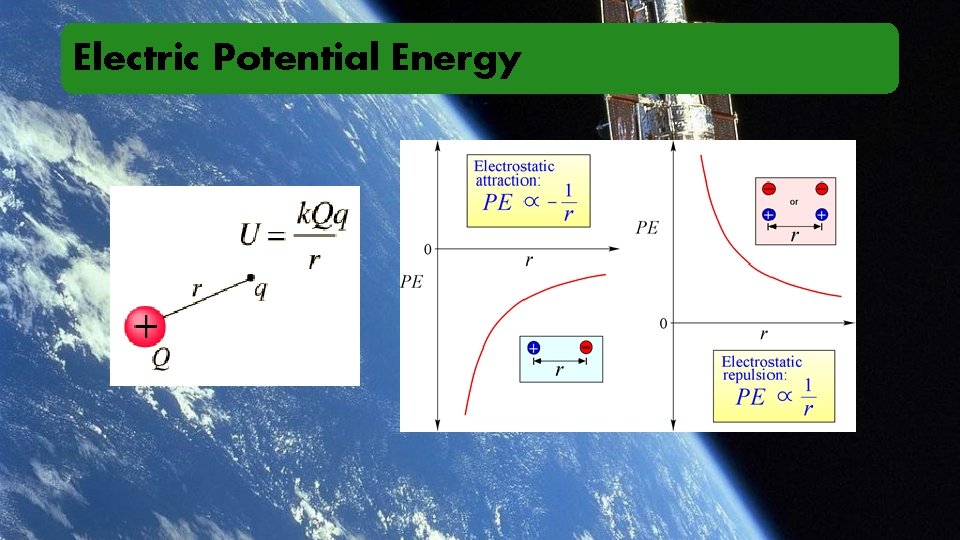
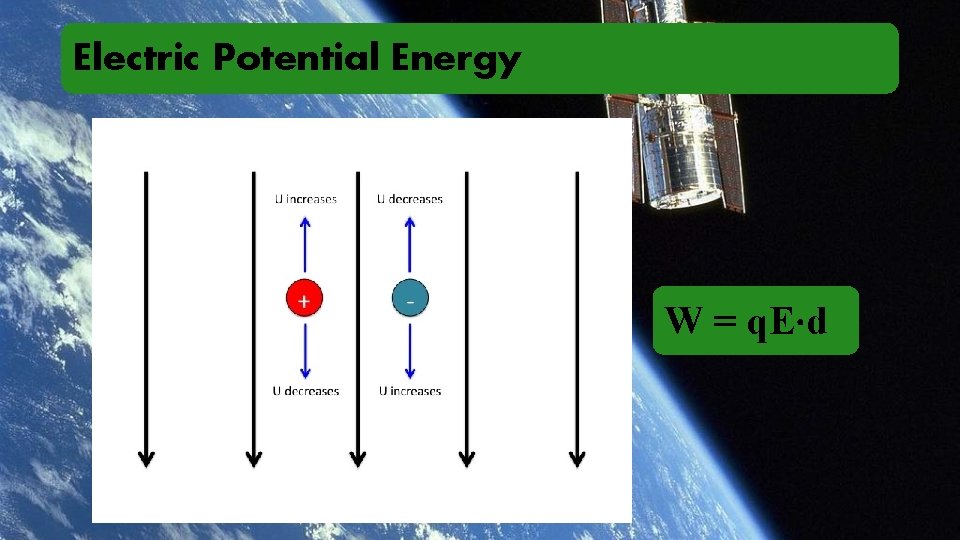
Electric Potential Energy

Electric Potential Energy W = q. E·d

Electric Potential Energy A fixed charge of +2 n. C rests at the origin. A second charge of +2 n. C and mass 0. 001 g is brought within a meter of the fixed charge and released. • Determine the potential energy of the charges when they are 1 m apart. • Determine how fast the second charge is moving when it is 10 m away. • Determine how fast the second charge is moving when it is infinitely far away.

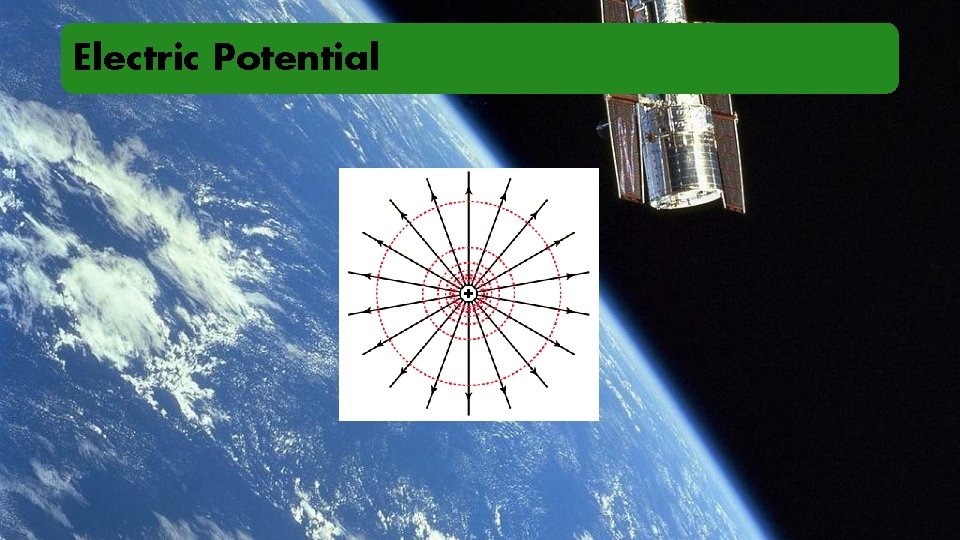
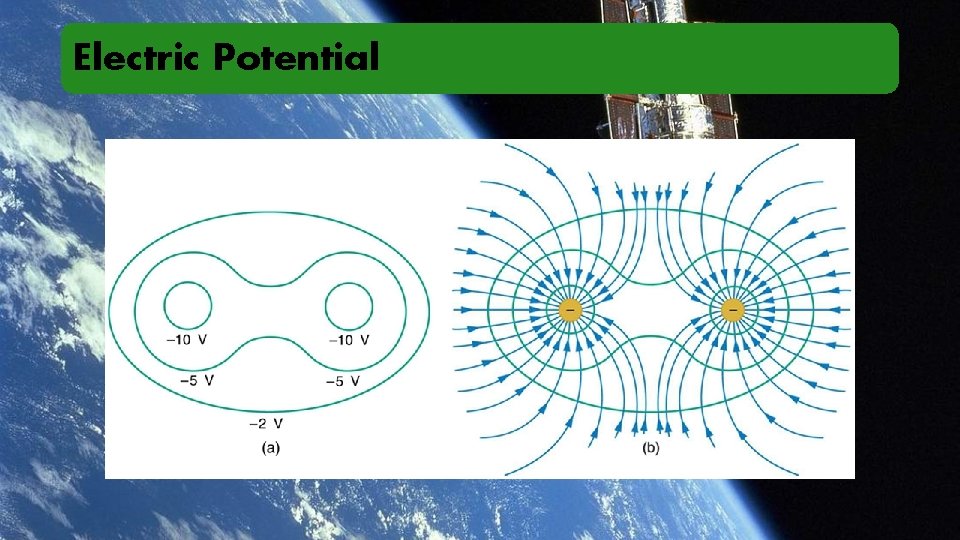
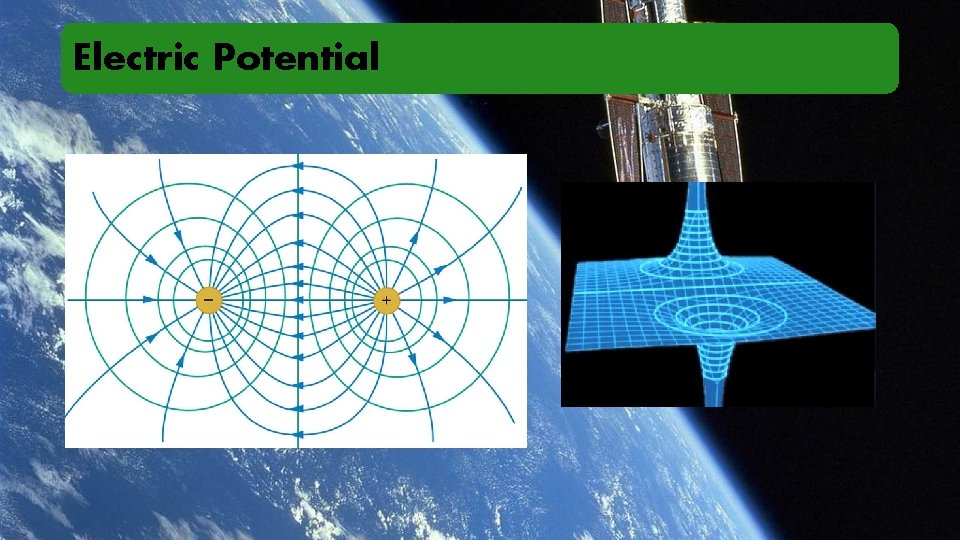
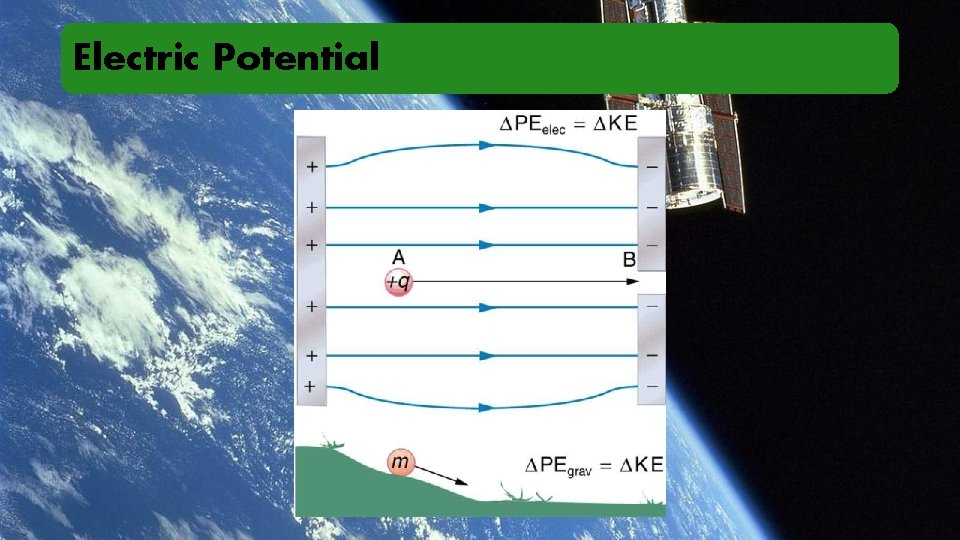
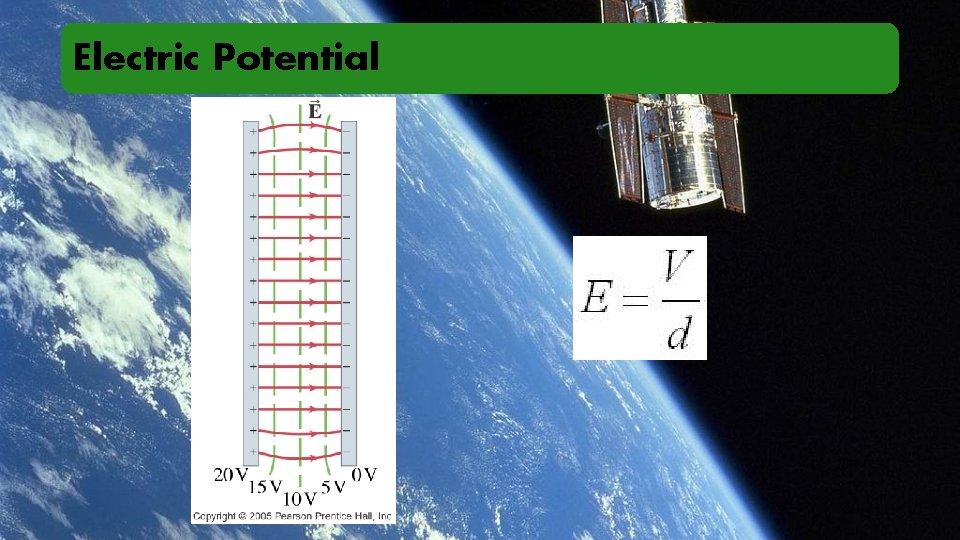
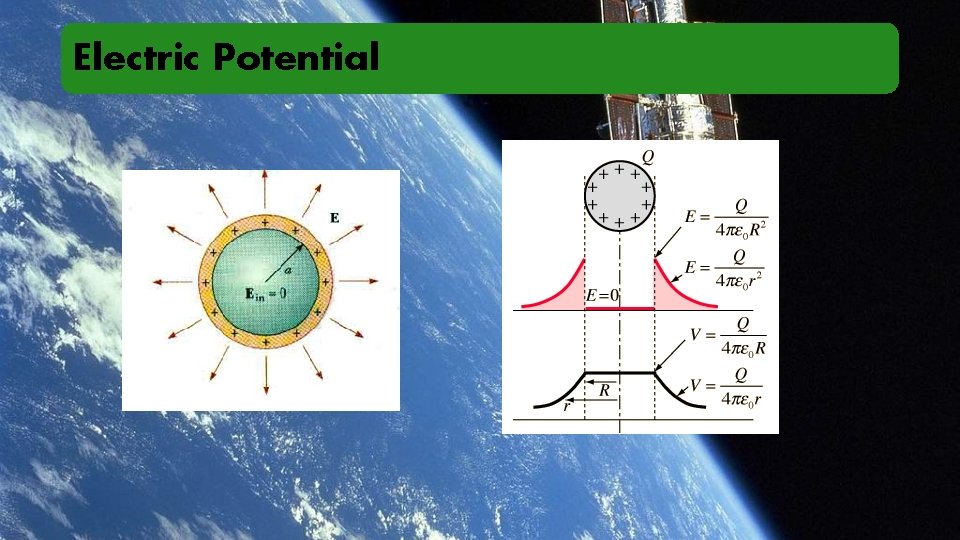
Electric Potential

Field Theory Summary

Electric Potential Given the diagram above, determine in what region the electric field would be zero. Determine in what region the electric potential would be zero. If the – 2 Q charge was replaced with a +2 Q charge, determine in what region the electric field would be zero. Determine in what region the electric potential would be zero. Given the diagram above, rank the points based on: • Electric Potential • Electric Field • Where a proton would have the most potential energy • Where an electron would have the most potential energy

Done!