Fibonacci series is defined as follows fib 0

Fibonacci series is defined as follows: fib (0) = 0 fib(1) = 1 fib(n) = fib(n-1) + fib(n-2) • Find a recursive algorithm for computing fib(n) and analyze its runtime • Find an iterative algorithm for computing fib(n) and analyze its runtime

Fibonacci series rec. Fib(n) { if (n ≤ 1) return n else return rec. Fib(n-1) + rec. Fib(n-2) } : אלגוריתם רקורסיבי קיבלנו נוסחת נסיגה = . 3 = 1∙(2(n-1)/2 -1 -1)/(2 -1) = 2(n-3)/2 -1

Fibonacci series rec. Fib(n) { if (n ≤ 1) return n else return rec. Fib(n-1) + rec. Fib(n-2) } קצב , לאומת 2 קטן פי n הירידה של 2

Fibonacci series iter. Fib (n) { allocate f[0. . n] f[0] = 0 f[1] = 1 for (i=2 ; i ≤ n ; i++) f[i] = f[i-1] + f[i-2] return f[n] } ~ פעולות T(n) פעולות n קיבלנו נוסחת נסיגה

Fibonacci series Recursive solution iter. Fib (n) { allocate f[0. . n] f[0] = 0 f[1] = 1 for (i=2 ; i ≤ n ; i++) f[i] = f[i-1] + f[i-2] return f[n] } ~ rec. Fib(n) { if (n ≤ 1) return n else return rec. Fib(n-1) + rec. Fib(n-2) } ? ? למה כזה הבדל בזמן ריצה . ואיטרציה לא , רקורסיה עושה אותו חישוב יותר מפעם אחת : תשובה

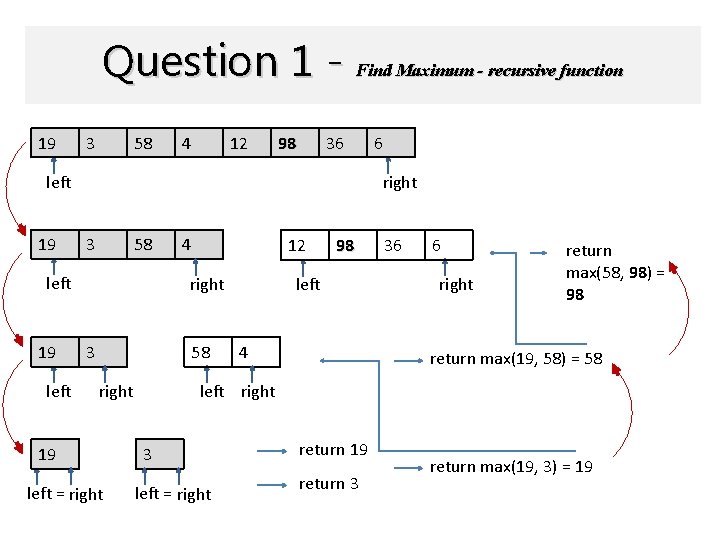
Question 1 - Find Maximum - recursive function 19 3 58 4 12 98 36 left 19 right 3 58 left 19 left 6 4 12 right 3 58 left = right left 4 36 6 right return max(58, 98) = 98 return max(19, 58) = 58 left right 19 98 3 left = right return 19 return 3 return max(19, 3) = 19

Question 1 public static int find. Max(int [ ] arr) { return Find. Max(arr, 0, arr. length-1); Find. Max } פעולות T(n) public static int find. Max( find. Max int a[ ], int left, int right ) { int middle; int max_l, max_r; if ( left == right ) return a[left]; else { middle = (left + right) / 2; פעולות T(n/2) max_l = Find. Max( Find. Max a, left, middle); פעולות T(n/2) max_r = Find. Max( Find. Max a, middle+1, right); return Math. max(max_l, max_r); } קיבלנו נוסחת נסיגה }