Fibonacci Numbers and Binet Formula An Introduction to

Fibonacci Numbers and Binet Formula (An Introduction to Number Theory) By: (The Ladies) 2

Recurrence Sequence • each further term of the sequence is defined as a function of the preceding terms (starting seed and rule) Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55. . . ) Lucas sequence (2, 1, 3, 4, 7, 11, 18, 29, 47, 76) • • • take 3+8 (1+2)+(3+5) (1+3)+(2+5) (4)+(7) - can be shown to hold in general

Mathematical induction • • • Fibonacci (1, 1, 2, 3, 5, 8, 13. . . ) 1, 1+1+2, 1+1+2+3+5, 1+1+2+3+5+8. . . 1, 2, 4, 7, 12, 20. . . +1 to each term 2, 3, 5, 8, 13, 21. . . because 1+1+2+3+5+8 1+1+1+2+3+5+8 (2+1)+2+3+5+8 (3+2)+3+5+8 (5+3)+5+8 (8+5)+8

Fibonacci sequence patterns Fibonacci (1, 1, 2, 3, 5, 8, 13. . . ) neither arithmetic nor geometric so write it in a different way 1/1=1 2/1=(1+1)/1 = (1+(1/1)) 3/2=(2+1)/2=1+(1/2)= 1+ 1/(1+(1/1)) 5/3=(3+2)/3=1+(2/3)=1+ 1/(1+(1/1))) and so on (Golden ratio φ)

Golden Ratio φ φ=1+1/φ φ2=φ+1 quadratic equation φ=(1+sqrt(5))/2 (only the positive answer) φ=1. 618033989. . .

Golden Ratio and practical application • • • most famous and controversial in history human aesthetics Converting between km and miles 1 mile= 1. 6093 km 13 km = 8 miles Fibonacci (1, 1, 2, 3, 5, 8, 13, 21. . . ) OK, using Fibonacci numbers, how many miles are in 50 kilometers? ? (show your work)

Binet Formula • • • A formula to find a term in a Fibonacci numbers without generating previous terms Jacques Binet in 1843 - known to Euler and Bernoulli 100 years before Fibonacci numbers are actually a combo of two geometric progressions • Recall φ2=φ+1 and τ2=τ+1 identities • Use them to come up with a formula for the Fibonacci

Binet Formula φ^n=Fnφ+Fn-1 τ^n=Fnτ+Fn-1 φ^n - τ^n=Fnφ - Fnτ Fn= (φ^n - τ^n) / (φ - τ) remember that φ = (1+sqrt(5))/2 and τ = (1+sqrt(5))/2 therefore (φ - τ) = sqrt (5) Fn= (φ^n - τ^n) / sqrt(5) Fn=(φ^n/sqrt(5)) - (τ^n/sqrt(5)) (two geometric progressions) now for the Fibonacci term 1000 is F 1000= (φ^(10000) - τ^(10000)) / sqrt(5) = 43466557686937456. . . (209 digits)

The Fibonacci Sequence in Nature http: //www. youtube. com/watch? v=ah. XIMUk. SX X 0

Application : The Towers of Hanoi

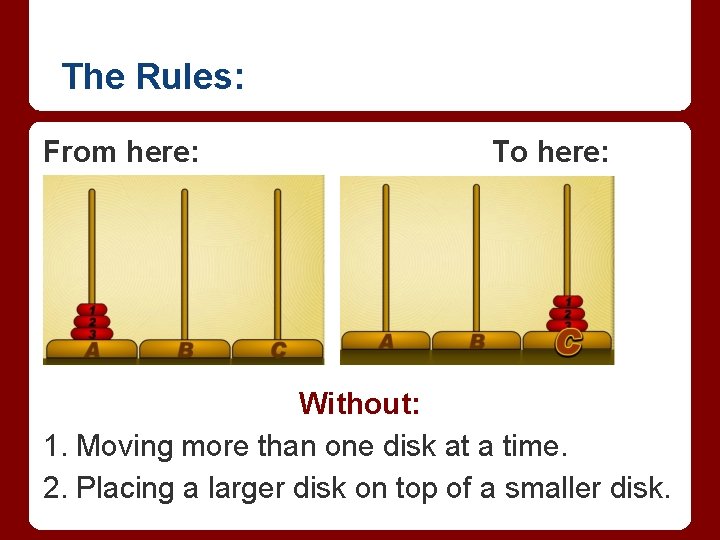
The Rules: From here: To here: Without: 1. Moving more than one disk at a time. 2. Placing a larger disk on top of a smaller disk.

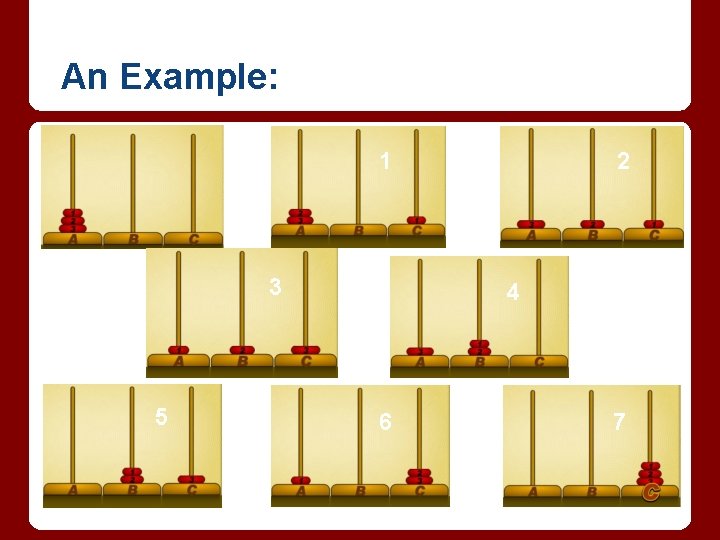
An Example: 1 3 5 2 4 6 7

The Goal: To find the minimum number of moves necessary to complete the puzzle. hn = # of moves required to transfer n disks. Let us find a recurrence rule to predict hn.

What We Know: h 3 = 7 h 7 = 123 h 4 = 15 = 247 h 5 = 31 h 6 = 63 hn = small disks + big disk + small disks hn-1 2 hn-1 +1 +1 + hn-1 h 8

Closed Formula: 3, 7, 15, 31, 63, . . . One less than a power of 2? 3 = 22 - 1 7 = 23 - 1 15 = 24 - 1 hn = 2 n -1

Prediction : End of the World? High on the mountaintops sat a monk who could foretell the end of the world. He had a Tower of Hanoi with 64 gleaming diamond disks and could move one a second. When he stopped the world would end. How long do we have?

Prediction : Solution Number of moves required 264 -1 So. . . roughly 583, 344, 214, 028 years.

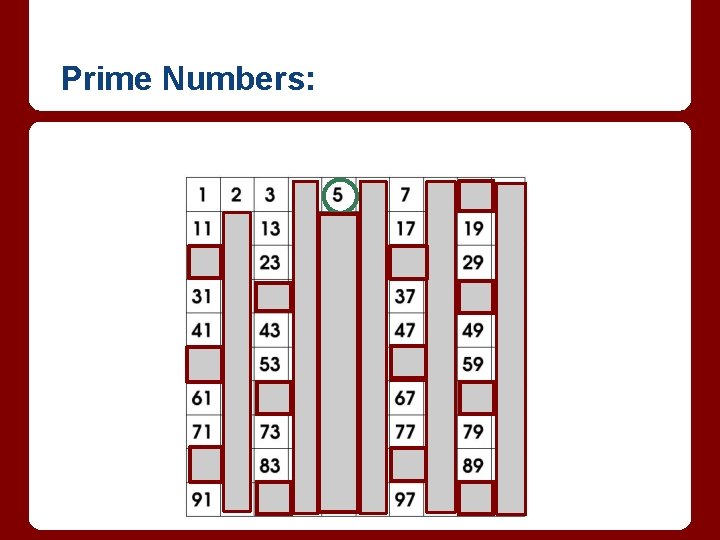
Prime Numbers: How do we find them? 200 B. C. Eratosthenes invented the sieve.

Prime Numbers:

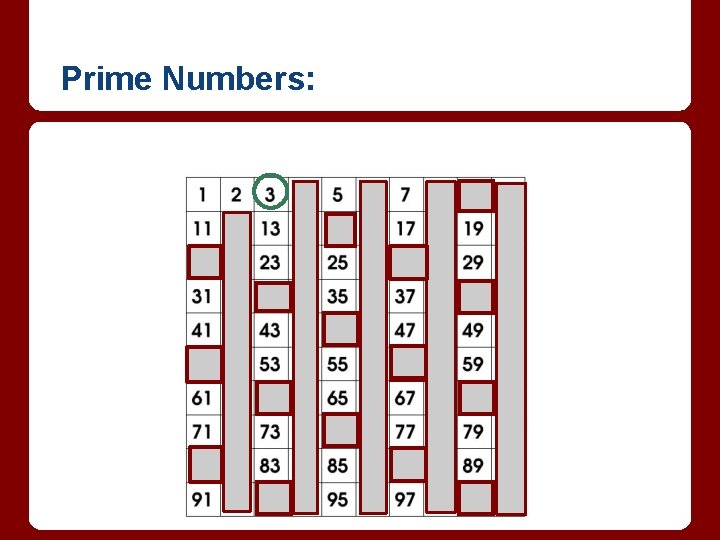
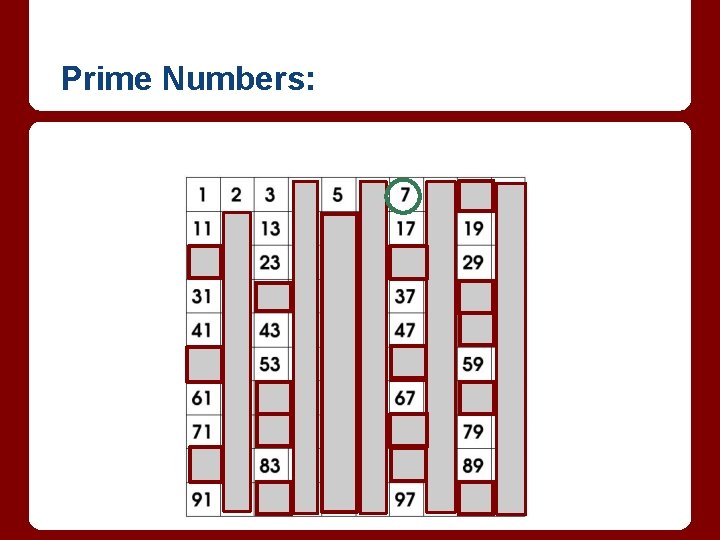
Prime Numbers:

Prime Numbers:

Prime Numbers:

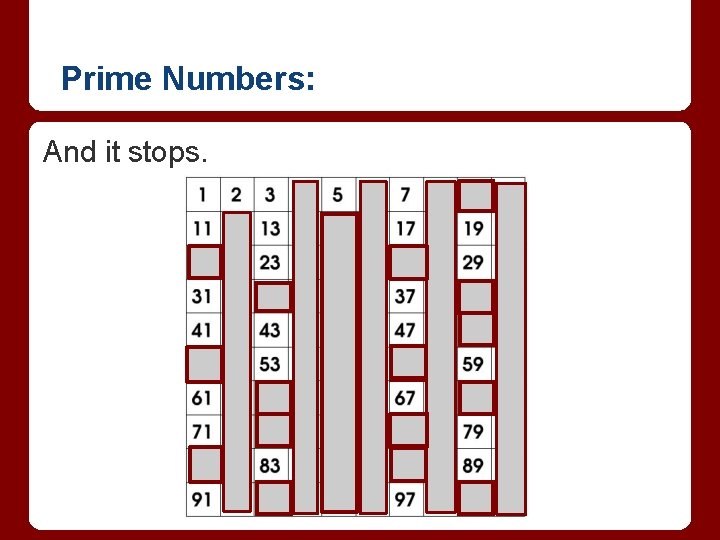
Prime Numbers: And it stops.

Why? The number of tests is the # of primes < testing maximum Proof by contradiction: 1. A composite exists in 11 -100 2. Thus, it is not a multiple of a P < 10 3. Thus, both factors > 10 4. Therefore, the composite > 100

Prime Numbers: How many exist? E = P 1 * P 2 * P 3 * P 4. . . Pn now. . . q = P 1 * P 2 * P 3 * P 4 *. . . * Pn + 1 Following the Composite Theorems (must be factor of unique prime numbers), infinite prime numbers exist.

Where Aren't the Prime Numbers? 2*3 + 2 = composite 2*3 + 3 = K = 2 * 3 * 4 *. . . * (N+1) K+2 = 2 * 3 * 4 *. . . * (N+1) +2 K+3 = 2 * 3 * 4 *. . . * (N+1) + 3 K+(N+1) = 2 * 3 * 4 *. . . * (N+1) + (N+1) K+2, K+3, K+4, K+(N+1) --> all composite,