Fiber tractoriented quantitative analysis of Diffusion Tensor MRI

Fiber tract-oriented quantitative analysis of Diffusion Tensor MRI data Isabelle Corouge Postdoctoral fellow, Dept of Computer Science and Psychiatry, UNC-Chapel Hill NAMIC: UNC – PNL collaboration -1 - October 7, 2005

Motivations • Diffusion Tensor MRI – Study white matter structural properties – Explore relationships between diffusion properties and brain connectivity • Motivations – – Inter-individual comparison Characterization of normal variability Atlas building Pathology (e. g. , tumor, fiber tract disruption) – Early brain development – Connectivity ? FA image NAMIC: UNC – PNL collaboration -2 - October 7, 2005

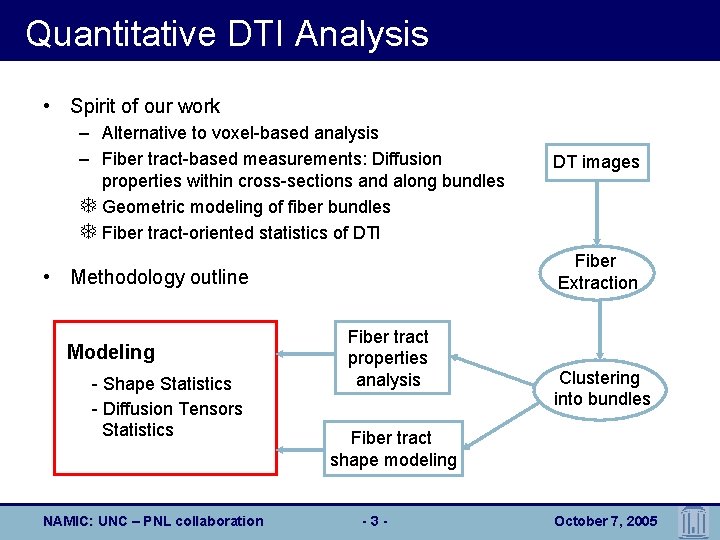
Quantitative DTI Analysis • Spirit of our work – Alternative to voxel-based analysis – Fiber tract-based measurements: Diffusion properties within cross-sections and along bundles T Geometric modeling of fiber bundles T Fiber tract-oriented statistics of DTI Fiber Extraction • Methodology outline Modeling - Shape Statistics - Diffusion Tensors Statistics NAMIC: UNC – PNL collaboration DT images Fiber tract properties analysis Clustering into bundles Fiber tract shape modeling -3 - October 7, 2005

Fiber Extraction • Extraction by tractography [Fillard’ 03] – High resolution DTI data (baseline + 6 directional images, 2 mm 3) – Principal diffusion direction tracking algorithm • Source and target regions of interest • Local continuity constraint, backward tracking, subvoxel precision • “Fibers”: streamlines through the vector field NAMIC: UNC – PNL collaboration -4 - October 7, 2005

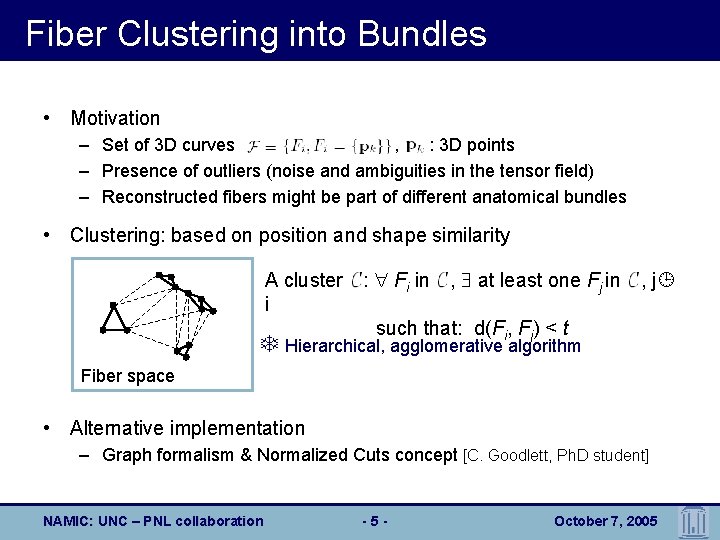
Fiber Clustering into Bundles • Motivation – Set of 3 D curves , : 3 D points – Presence of outliers (noise and ambiguities in the tensor field) – Reconstructed fibers might be part of different anatomical bundles • Clustering: based on position and shape similarity A cluster C: Fi in C, at least one Fj in C, j i such that: d(Fi, Fj) < t T Hierarchical, agglomerative algorithm Fiber space • Alternative implementation – Graph formalism & Normalized Cuts concept [C. Goodlett, Ph. D student] NAMIC: UNC – PNL collaboration -5 - October 7, 2005

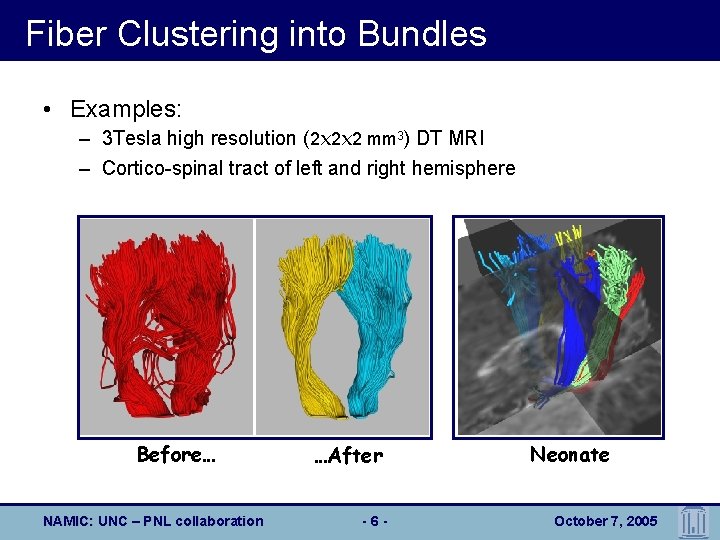
Fiber Clustering into Bundles • Examples: – 3 Tesla high resolution (2 x 2 x 2 mm 3) DT MRI – Cortico-spinal tract of left and right hemisphere Before… NAMIC: UNC – PNL collaboration …After -6 - Neonate October 7, 2005

Fiber Clustering into Bundles • Graph-theoretic approach Longitudinal fasciculus (2312 streamlines) 6 clusters Fornix cluster * Images from Casey Goodlett NAMIC: UNC – PNL collaboration -7 - October 7, 2005

Fiber Tract Properties Analysis • Analysis across fibers – Local shape properties: curvature/torsion – Diffusion properties: FA, MD, … • Matching scheme – Definition of a common origin for each bundle – Parameterization of the fibers: cubic B-splines – Explicit point to point matching according to arclength • Computation of pointwise mean and standard deviation of these features NAMIC: UNC – PNL collaboration -8 - October 7, 2005

Local Shape Properties a b c For each curve Curvature Mean ± σ a a b c Adult 1 Adult 2 NAMIC: UNC – PNL collaboration -9 - c b Neonate October 7, 2005

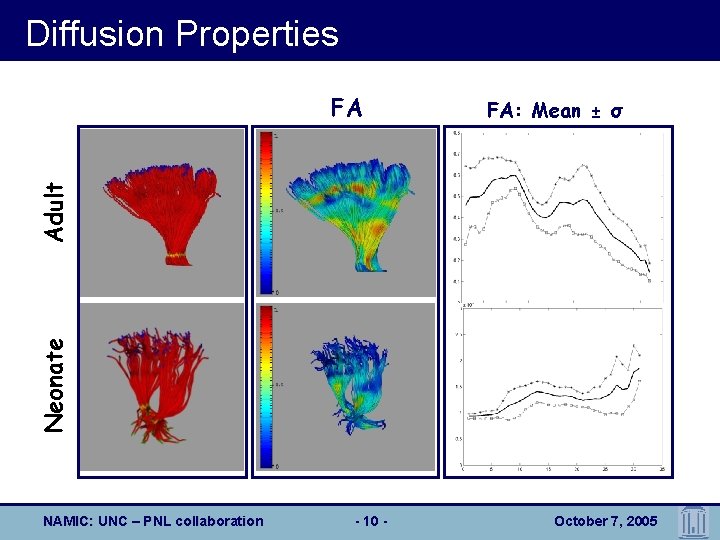
Diffusion Properties FA: Mean ± σ Neonate Adult FA NAMIC: UNC – PNL collaboration - 10 - October 7, 2005

Geometric Modeling of Individual Fiber Tracts • Statistical modeling based on variability learning • Construction of a training set – Parametric data representation – Matching: • Dense point to point correspondence • Pose parameter estimation: Procrustes analysis • Estimation of a template curve: mean shape • Characterization of statistical shape variability – Multidimensional statistical analysis: PCA NAMIC: UNC – PNL collaboration - 11 - October 7, 2005

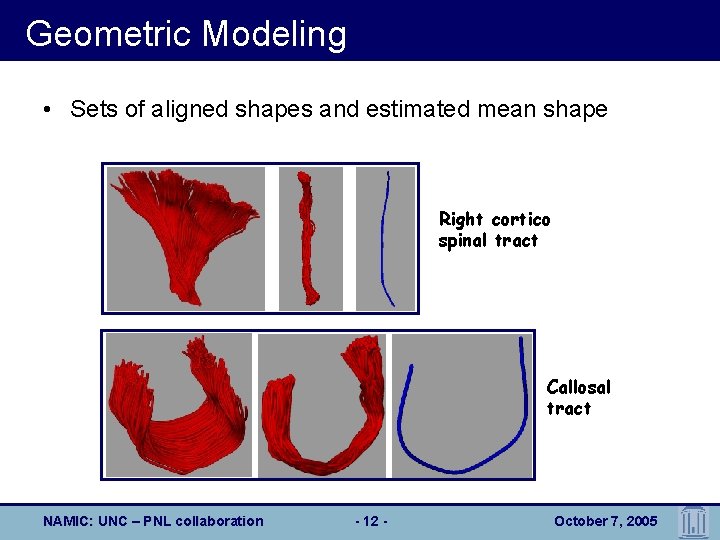
Geometric Modeling • Sets of aligned shapes and estimated mean shape Right cortico spinal tract Callosal tract NAMIC: UNC – PNL collaboration - 12 - October 7, 2005

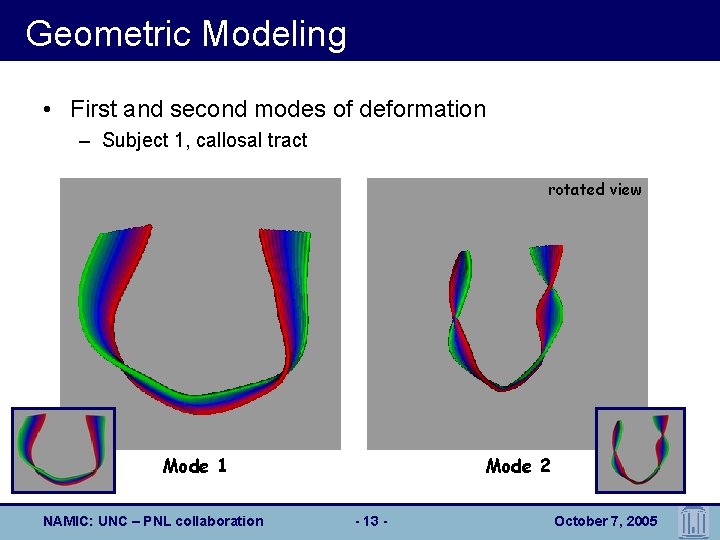
Geometric Modeling • First and second modes of deformation – Subject 1, callosal tract rotated view Mode 2 Mode 1 NAMIC: UNC – PNL collaboration - 13 - October 7, 2005

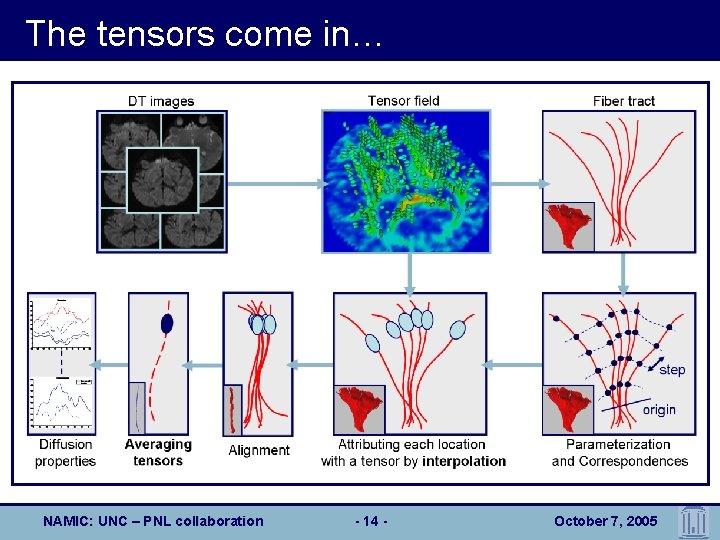
The tensors come in… NAMIC: UNC – PNL collaboration - 14 - October 7, 2005

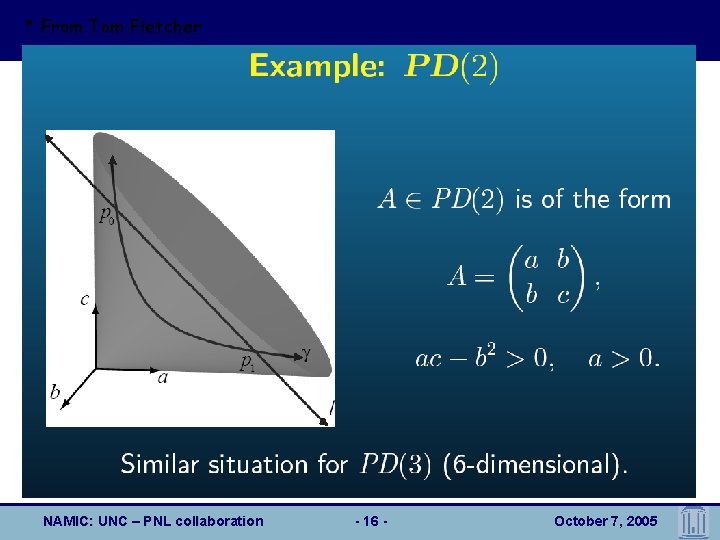
Tensor Statistics and Tensor Interpolation • Tensor: 3 x 3 symmetric definite-positive matrix • PD(3): space of all 3 D tensors – PD(3) is NOT a vector space Þ Linear statistics are not appropriate ! NAMIC: UNC – PNL collaboration - 15 - October 7, 2005

* From Tom Fletcher NAMIC: UNC – PNL collaboration - 16 - October 7, 2005

Tensor Statistics and Tensor Interpolation • Tensor: 3 x 3 symmetric definite-positive matrix • PD(3): space of all 3 D tensors – PD(3) is NOT a vector space Þ Linear statistics are not appropriate ! Linear Properties Positive-definiteness NO Determinant NAMIC: UNC – PNL collaboration NO - 17 - Sym. Space YES October 7, 2005

Tensor Statistics and Tensor Interpolation • Tensor: 3 x 3 symmetric definite-positive matrix • PD(3): space of all 3 D tensors – PD(3) is NOT a vector space Þ Linear operations are not appropriate ! Linear Properties Positive-definiteness NO Determinant NO Sym. Space YES • PD(3) is a Riemannian symmetric space NAMIC: UNC – PNL collaboration - 18 - October 7, 2005

Geodesic distance * From Tom Fletcher • Algebraic computation NAMIC: UNC – PNL collaboration - 19 - October 7, 2005

Tensor Statistics and Tensor Interpolation • Average of a set of tensors • Variance of a set of tensors • Interpolation of tensors: weighted-average NAMIC: UNC – PNL collaboration - 20 - October 7, 2005

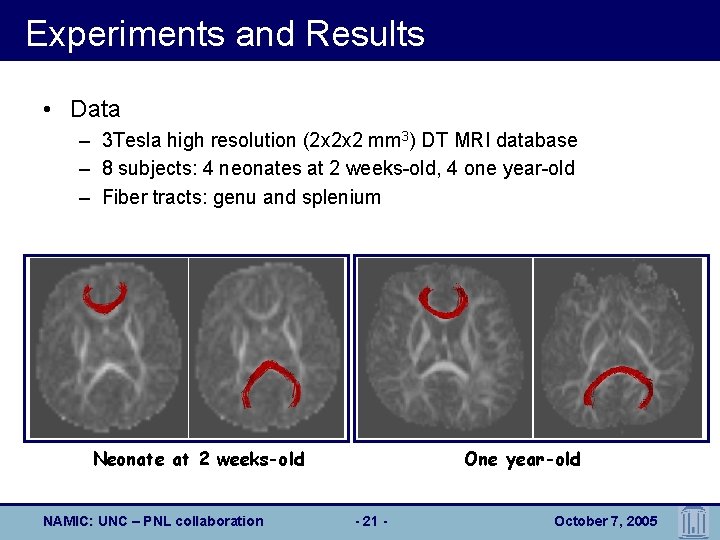
Experiments and Results • Data – 3 Tesla high resolution (2 x 2 x 2 mm 3) DT MRI database – 8 subjects: 4 neonates at 2 weeks-old, 4 one year-old – Fiber tracts: genu and splenium Neonate at 2 weeks-old NAMIC: UNC – PNL collaboration One year-old - 21 - October 7, 2005

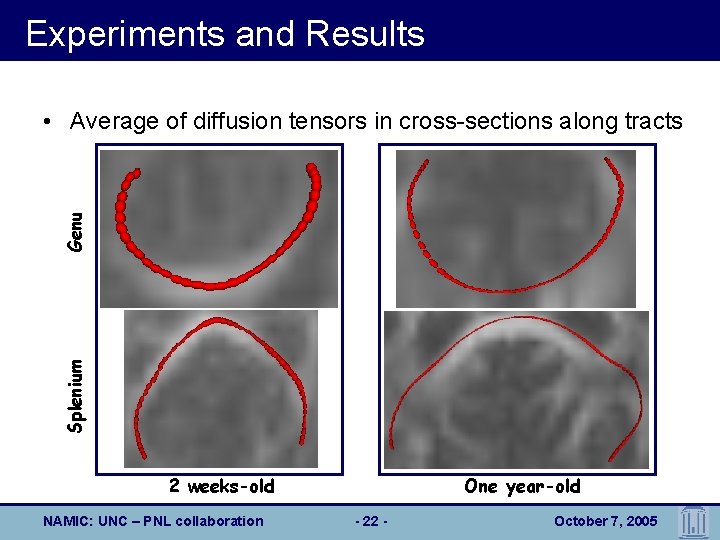
Experiments and Results Splenium Genu • Average of diffusion tensors in cross-sections along tracts 2 weeks-old NAMIC: UNC – PNL collaboration One year-old - 22 - October 7, 2005

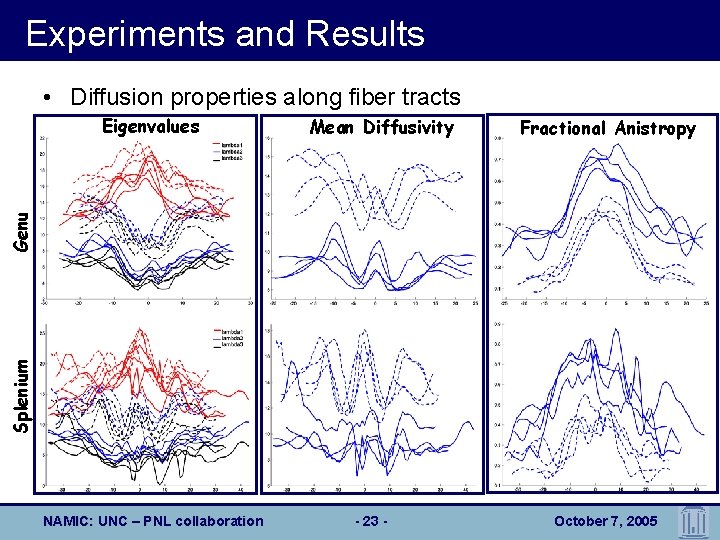
Experiments and Results • Diffusion properties along fiber tracts Mean Diffusivity Fractional Anistropy Splenium Genu Eigenvalues NAMIC: UNC – PNL collaboration - 23 - October 7, 2005

Future Work • Inter-individual comparison – Fiber-tract based coordinate system • Representation of a fiber tract – Prototype curve + space trajectory • Definition of the space trajectory – Representation by cables/ribbon-bundles/manifold • Geodesic anisotropy • Hpothesis testing NAMIC: UNC – PNL collaboration - 24 - October 7, 2005

Acknowledgements • The team – – – – – • Software development – ITK, VTK, Qt – Julien Jomier (UNC) Guido Gerig (UNC) Casey Goodlett (UNC) Weili Lin (UNC) Sampath Vetsa (UNC) Tom Fletcher (Utah) Rémi Jean Matthieu Jomier (France) Sylvain Gouttard (France) Clément Vachet (France) NAMIC: UNC – PNL collaboration - 25 - October 7, 2005