Fggvnyjellemzk A diasorozat az Analzis 1 Mozaik Kiad

Függvényjellemzők A diasorozat az Analízis 1. (Mozaik Kiadó 2005. ) c. könyvhöz készült. Készítette: Dr. Ábrahám István 1

A függvények jellemzői A függvényjellemzők segítségével vizsgálhatjuk a függvények növekedését és csökkenését, optimumokat határozhatunk meg, valamint más fontos ismerethez juthatunk. 1. Korlátosság Az f(x) függvény korlátos, ha minden függvényérték két valós szám között található: (Az egyenlőség nem szükségszerű. ) A korlátossághoz mindkét korlát létezése szükséges. Példa: az y=x 2 nem korlátos, van ugyan alsó korlát (a nulla), de nincs felső korlát. Az y=sinx korlátos, Ka=– 1 és Kf=1. Ha a függvény korlátos, akkor végtelen sok alsó, illetve felső korlátja van. Pontos alsó korlát (alsó határ) a létező alsó korlátok közül a legnagyobb, a felső határ (pontos felső korlát) pedig a lehetséges felső korlátok közül a legkisebb érték. Például: az De az függvénynek nincsenek korlátai: függvény korlátos: Ka=0, 5; Kf=1. Ezt így is jelölhetjük: Ka=min f(x)=f(2)=0, 5, és Kf=max f(x)=f(1)=1. 2

2. Monotonitás Az f(x) függvény szigorúan monoton növekvő, ha bármely x 2>x 1 -re igaz, hogy f(x 2)>f(x 1). (Természetesen az x-ek az értelmezési tartományból származnak. ) Növekvő a függvény, ha „az x-ek növekedtével az y értékek is nagyobbak lesznek. ” Csökkenő a függvény, ha „az x-ek növekedtével az y értékek egyre kisebbek lesznek. ” Monoton növekvő a függvény, ha bármely x 2>x 1 esetén f(x 2) f(x 1), csökkenő: f(x 2) f(x 1). A sorozat jellemzői és a függvényjellemzők között analógia van, hiszen a sorozat tulajdonképpen speciális függvény, ahol az értelmezési tartomány a sorszámok halmaza (N+). Például: az függvény nem monoton, mert az x értékek növekedtével a függvényérték egyszer nőtt, másszor csökkent. Hiszen az x 1=– 1 esetén az f(x 1)=– 1 és az x 2=1 értékénél az f(x 2 )=1, de x 3=2 -nél f(x 3)=0, 5. Ugyanakkor az függvény szigorúan monoton csökken. A monotonitást is gyakran az értelmezési tartomány egy részén, egy adott intervallumon vizsgáljuk. Példa: az f(x)=x 2 a negatív x-ek tartományán csökkenő, a pozitívoknál növekvő. 3 Az f(x)=állandó függvényre (képe az x tengellyel párhuzamos egyenes) nem vezetünk be külön kategóriát, a konstans függvényt egyszerre növekvőnek és csökkenőnek mondjuk.

3. Paritás Elnevezés: ha a függvény értelmezési tartománya olyan, hogy x ÉT esetén mindig –x is eleme az értelmezési tartománynak, valamint minden x-re igaz, hogy: f(x)=f(–x), akkor a függvényt párosnak nevezzük. Az értelmezési tartománynak szimmetrikusnak kell lennie, azaz pozitív és negatív előjellel is szerepelniük kell az azonos abszolút értékű elemeknek. Például: az x 2 függvény páros, mert mindig igaz, hogy: f(–x)=f(x). (Hiszen (–x)2=x 2. ) Vigyázat! Az f: f(x)=x 2, x R+ függvény nem páros, mert az értelmezési tartománya nem szimmetrikus 0 -ra. A páros függvények gráfja az y tengelyre szimmetrikus. Definició: az f függvény páratlan, ha x Df –x Df és az értelmezési tartomány minden x elemére az f(–x)=–f(x) feltétel teljesül. Például: az x 3 függvény páratlan, mert mindig igaz, hogy f(–x) = –f(x). A páratlan függvények gráfja a koordinátarendszer kezdőpontjára (az origóra) szimmetrikus. (Ha x R). A függvények többnyire nem mutatnak paritást, azaz a legtöbb függvény se nem páros, se nem páratlan. Például: az y=x+1 függvény nem mutat paritást. (f(–x) f(x), és f(–x) –f(x). ) 4

4. Periodicitás Csak a függvények néhány típusára jellemző ez a tulajdonság, amelynek lényege az, hogy rendszeres ismétlődéssel azonos függvényértékek fordulnak elő. Elnevezés: az f függvény p szerint periódikus, ha minden x-re igaz, hogy x Df esetén x+kp Df és f(x)=f(x+kp), ahol p>0 és k Z. Példaként leggyakrabban a trigonometrikus függvényeket említjük, hiszen ismert, hogy: sinx=sin(x+2 k ), vagy tgx=tg(x+ k ), ahol k Z. Léteznek olyan periodikus függvények is, amelyek nem trigonometrikusak, például: y={x}, x R+. A függvények alaposabb vizsgálatánál néhány további, főként a függvény vizsgálatához, ábrázolásához kapcsolódó jellemzőt is tárgyalni fogunk. Ilyen például a függvény vonalának görbülete, vagy az aszimptoták). Igen lényeges jellemzője a függvényeknek a határérték és a folytonosság. 5. A függvény határértéke Bevezetőül: 1. Bármely x 0 számhoz (a számegyenesen egy ponthoz) meg tudunk adni hozzá konvergáló, valós számokból álló sorozatot. Például: az f: f(x)=2 x+1 függvénynél az x 0=3 ponthoz konvergáló sorozat: 2. Bármely számhoz végtelen sok, hozzá konvergáló sorozat adható meg, 5 például úgy, hogy a számhoz hozzáadunk egy tetszőleges nullsorozatot.

Például: az f(x)=2 x+1 függvénynél az x 0 =3 és legyen: Ekkor az függvényérték sorozat elemei: és így tovább. f(4)=9; A függvény utasításába (vedd a független változó kétszeresét és adj hozzá 1 -et) helyettesíthetjük az (xn) sorozat elemeit. A függvényértékek sorozatának is lehet határértéke. Ha általánosan, n-nel írjuk fel a 3 -hoz tartó sorozatot, akkor a függvényértékek sorozata: , akkor: Igaz: A függvényérték sorozat határértéke tehát 7. Eredményünket így is írhatjuk: Definíció: az f(x) függvénynek az x 0 helyen határértéke az A, ha minden (xn) sorozatra Feltétel még: a függvény az x 0 környezetében értelmezve legyen. A függvényhatárérték jelölése: 6

A definícióban szereplő minden (xn) sorozatnak ténylegesen tetszőlegesnek kell lennie. Tehát az x 0 -hoz a sorozat nemcsak jobbról, vagy balról konvergálhat, hanem egyszerre mindkét oldalról. Például: az x 0=3 -hoz jobbról konvergál az sorozat. A kapott függvényérték sorozat határértékét jobboldali határértéknek nevezzük. Jelölése: Másképp: Az x 0+0 csupán jelölés, a jobbról való közeledést fejezi ki. Értelmezhetjük a függvény baloldali határértékét: Ha az x 0 -hoz minden balról konvergáló (xn) sorozat esetén (ekkor a sorozat minden tagjára: xn< x 0) a függvényértékek sorozata tart Ab-hez, akkor Ab baloldali határérték. Jelölése: Az x 0– 0 szintén csupán jelölés, a balról való közeledést fejezi ki. Ahhoz, hogy a függvény határértéke létezzen az x 0 helyen, szükséges és elegendő, hogy mind a baloldali, mind a jobboldali határértékek létezzenek és megegyezzenek. Nemcsak az 1/n sorozattal lehet az adott x 0 -hoz balról-, illetve jobbról konvergáló sorozatot készíteni. Legtöbbször azonban dolgozhatunk az egyszerű, „jól kiismert” 1/n sorozattal. Például: az f: f(x)=2 x+1 függvénynek a 3 helyen vett jobboldali határértékéhez: Ekkor: A baloldalihoz: A bal- és jobboldali határértékek megegyeznek, tehát: 7

Például: legyen Számoljuk ki az x 0=1 helyen a határértéket! A baloldali határértékhez: Ekkor: A jobboldali határértékhez: Ekkor: Látható, hogy Ab Aj, ezért a függvényünknek az x 0=1 helyen nincs határértéke. A határértéket általában speciális esetekben is számolhatjuk sorozatok segítségével. Speciális eseten a függvény szakadási helyein, illetve a +, vagy – végtelenben vett határértéket értjük. Például: mi a határértéke az függvénynek a 0 helyen? Legyen: A jobboldali határérték kiszámolása: A bal- és jobboldali határérték nem egyezik meg, tehát a függvényünknek nincs határ 8 értéke a 0 helyen.

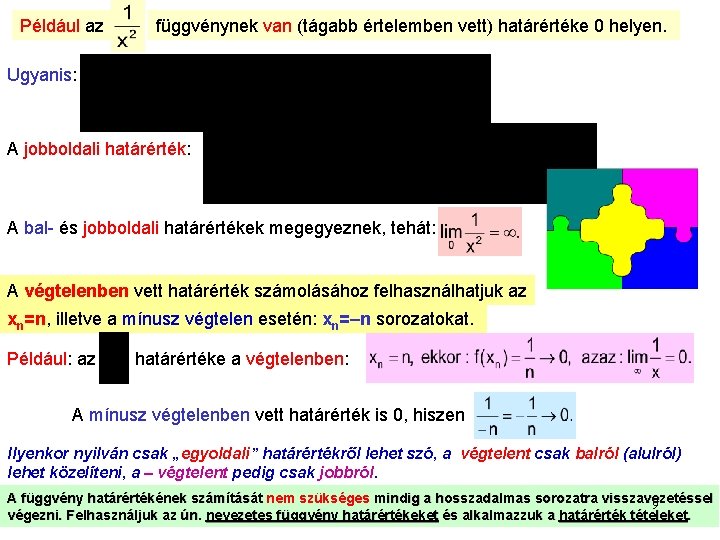
Például az függvénynek van (tágabb értelemben vett) határértéke 0 helyen. Ugyanis: A jobboldali határérték: A bal- és jobboldali határértékek megegyeznek, tehát: A végtelenben vett határérték számolásához felhasználhatjuk az xn=n, illetve a mínusz végtelen esetén: xn=–n sorozatokat. Például: az határértéke a végtelenben: A mínusz végtelenben vett határérték is 0, hiszen Ilyenkor nyilván csak „egyoldali” határértékről lehet szó, a végtelent csak balról (alulról) lehet közelíteni, a – végtelent pedig csak jobbról. A függvény határértékének számítását nem szükséges mindig a hosszadalmas sorozatra visszavezetéssel 9 végezni. Felhasználjuk az ún. nevezetes függvény határértékeket és alkalmazzuk a határérték tételeket.

Határérték tételek 1. A határérték képzés művelettartó. Ez azt jelenti, hogy ha: akkor: és hasonlóan igaz a művelettartás a szorzásra, az osztásra, sőt, a függvényutasítások egymásutánjára (összetett függvény!) is. (Természetesen bizonyos feltételekkel, tehát például a hányados képzésnél a nevezőben nem lehet 0, vagy az összetett függvénynél nem lehet „baj” az értelmezési tartománnyal. ) Az összefüggések analógok a sorozatoknál megismertekkel, azok igazolása is a sorozatokra visszavezetve egyszerű. Például: láttuk korábban, hogy A művelettartás miatt ekkor: 2. Érvényes a „rendőr szabály” is, azaz ha: valamint a h(x) olyan függvény, hogy f(x) h(x) g(x), akkor: A „közrefogott” függvény határértéke megegyezik a közrefogó függvények közös határértékével (ha az értelmezési tartományokkal sincs probléma). A szabály igazolása sorozatokkal egyszerű. 10

Nevezetes függvényhatárértékek 1. A „sorozat-analóg” határértékek: Következmény: az e számhoz konvergáló sorozatot átírhatjuk: , hiszen ha Ebből: (Az x>– 1 a logaritmálás miatt). Emlékszünk: ha a logaritmus alapja az e szám, akkor ln a logaritmus jele. 2. Exponenciális és lineáris függvény hányadosára: Bizonyítás: lásd tankönyv. Bizonyítás: válasszuk az x-eket a ] 0; /2 [ szakaszból. Rajzolhatunk: Az OAB háromszögben: AB=sinx (mert OB=1), a CB ív hossza x (radián), az OCD háromszögben: DC=tgx (mert OC=1). Felírható (látható is): Osztunk a (pozitív) sinx-szel és reciprokot képezünk: Ebből: (Művelettartás, rendőrszabály 11 miatt. )

A 3. tétel levezetésben kapott határérték jobboldali, hiszen a pozitív x-ek felől közelítettük a nullát. De ismert: tehát a fenti igazolás a negatív x-ekre hasonlóan elvégezhető, a baloldali határérték is 1, így általánosan igaz az állítás. Példa: mert (bizonyítható) a sin(„valami”) osztva ugyanazzal a „valami”-vel határértékben 1, ha az a „valami” tart 0 -hoz. A határérték számolásnál néha trükköket alkalmazunk. Példa: Igaz: Ezt felhasználva: Megjegyzés: a függvényhatárérték számolásnál meghatározóan fontos, hogy hol, milyen változó értéknél vesszük a határértéket. Tehát, ha a lim „alá” nem írunk semmit, akkor a határérték nem számolható! Mást jelent és nem nevezetes például a határérték, ha például a 2 helyen vesszük: 12

6. A függvény folytonossága A matematikában a függvény folytonosságát pontbeli tulajdonságként értelmezzük. Definíció: az f(x) függvény folytonos egy x 0 pontban, ha egyszerre eleget tesz a következő 3 feltételnek: a függvényt értelmeztük az x 0 -ban és annak környezetében (van helyettesítési érték); van határértéke a függvénynek az x 0 pontban; a határérték megegyezik a helyettesítési értékkel, azaz: Fontos! A függvény gráfját (vonalát, görbéjét, képét) legtöbbször folyamatos „vonalhúzással” állítottuk elő. Ez a gyakorlat nem mindig követhető! Például: Például Ha a függvényutasítás: a függvényérték f(x)=1, ha x racionális szám. Ebben a függvényértékek „végtelenül közel” vannak egymáshoz, hiszen bármely racionális számhoz végtelenül közel végtelen sok racionális szám van. Ugyanakkor minden (x; f(x)) függvénypont között „lyuk” van, mert bármely két racionális szám között van irracionális szám, tehát a definiált függvénypontok nem köthetők össze! Értelmezés: az f(x) függvény az x 0 pontban balról folytonos, ha „csak” a baloldali határérték egyezik meg a helyettesítési értékkel: 13

A jobboldali folytonosságnál: Például: az f(x)=[x] (egész rész függvény) az x 0=2 helyen: A függvény helyettesítési értéke: f(2)=2, a baloldali határérték 1, a jobboldali határérték 2, így a függvény jobbról folytonos, balról nem. Definíció: az f(x) függvény az értelmezési tartományának egy szakaszán (egy intervallumon) folytonos, ha az intervallum minden pontjában folytonos. A függvény folytonos lehet a teljes értelmezési tartományán is. Nevezetes folytonos függvények 1. A hatványfüggvények (f: f(x)=xn), ha n pozitív egész, mindenütt folytonosak. Példa: az f(x)=x függvénynél az értelmezési tartomány tetszőleges x 0 pontjában a helyettesítési érték: f(x 0). A határérték: A határérték egyenlő a helyettesítési értékkel, tehát a függvény folytonos. Tétel: A hatványfüggvények minden más n kitevő értéknél is folytonosak minden olyan A tételt nem bizonyítjuk. helyen, ahol nincs szakadási helyük. Az igazolásokat az f(x)=x-nél látottakhoz hasonlóan egyszerűen elvégezhetjük. 14

2. A trigonometrikus függvények (sinx, cosx, tgx, ctgx) folytonosak mindenütt, ahol nincs szakadásuk. 3. Az exponenciális (y=ax) és logaritmus függvények is teljes értelmezési tartományukon folytonosak. Az alapfüggvények folytonosságának ismerete a határérték számítást is egyszerűsíti: ha tudjuk, hogy a függvény x 0 pontban folytonos, akkor a helyettesítési értéke lesz egyúttal a határérték. Például: az f(x)=x 6 határértéke az x 0=2 pontban: Tétel: A folytonosság művelettartó. Tehát: Tehát két folytonos függvénnyel műveletet végezve (alapműveletek, összetett függvény képzés) a kapott új függvény is folytonos lesz, mindazokon a helyeken, ahol a művelettel az értelmezési tartomány nem sérül, nem szűkül, a művelettel nem keletkezik szakadása. Példa: az f(x)=x 2– 5 x+6 valamint a g(x)=x 2– 4 mindenütt folytonosak, összegük, különbségük, szorzatuk szintén, de a hányadosuk nem mindenütt! Ugyanis: Ez a hányadosfüggvény nem folytonos ott, ahol a nevező: x 2 -4= 0. Az x=2 helyen (itt megszűntethető a szakadás, a nevezőt „nullává tevő” tényező ugyanolyan alakban szerepel a számlálóban is), és az x=– 2 helyen, itt a szakadás nem megszűntethető. 15

Gyakorló feladat: adott az függvény. Milyen értékeket adjunk az a, b és c számoknak, ha azt akarjuk, hogy a függvényünk minden valós számra folytonos legyen? A tört két folytonos függvény hányadosa, ami folytonos, ahol a nevező nem nulla. Átalakítás: Tehát nem folytonos a függvényünk az x 1=0, az x 2=1 és az x 3=-1 helyeken. Olyan függvényértékeket kell megadnunk az adott pontokban, hogy megszűntessük a „folytonosság hiányát”, azaz a helyettesítési érték a határértékkel egyezzen meg. Az x 1=0 helyen legyen Ekkor: A bal- és jobboldali határérték nem egyezik meg, tehát nincs határérték, így folytonossá 16 sem tehető a függvény az x 1=0 pontban.

Az x 2=1 helyen a határérték képzés előtt elvégezhető a következő átalakítás: A képlettel adott függvényünknek megszűntethető szakadása van az x 2=1 pontban. Ez azt jelenti, hogy az folytonos ezen a helyen, így: Ha úgy döntünk, hogy az x=1 helyen a függvényérték -1, 5 legyen, akkor ott a függvény folytonos lesz (a függvényérték egyenlő lesz a határértékkel). Az x 3=– 1 helyen szintén az igaz, hogy a baloldali határérték nem egyezik meg a jobboldalival, tehát nincs határérték, azaz folytonossá sem tehető a függvény. A fejezet tárgyalását befejeztük. 17