FFT in Hardware and Software Background Core Algorithm

FFT in Hardware and Software

Background • Core Algorithm • Original Algorithm, the DFT, O(n 2) complexity • New Algorithm, the FFT (Fast Fourier Transform), O(nlog 2(n)) depending on implementation.

DFT Computation • A summation over the whole input array for every single element in the output array. • A VERY computationally inefficient algorithm to implement.

FFT Computation • A much more computationally efficient algorithm • Works using the divide and conquer principle. • First developed by Cooley and Tukey in 1965!

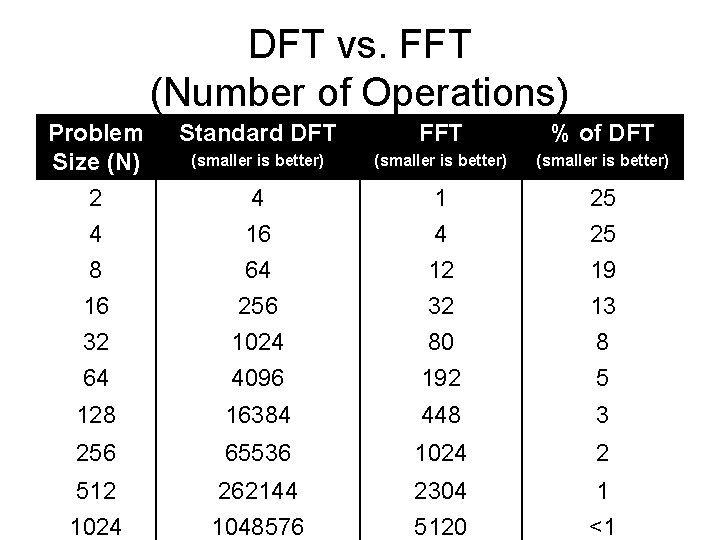
DFT vs. FFT (Number of Operations) Problem Size (N) 2 4 Standard DFT FFT % of DFT (smaller is better) 4 16 1 4 25 25 8 16 32 64 64 256 1024 4096 12 32 80 192 19 13 8 5 128 16384 448 3 256 65536 1024 2 512 1024 262144 1048576 2304 5120 1 <1

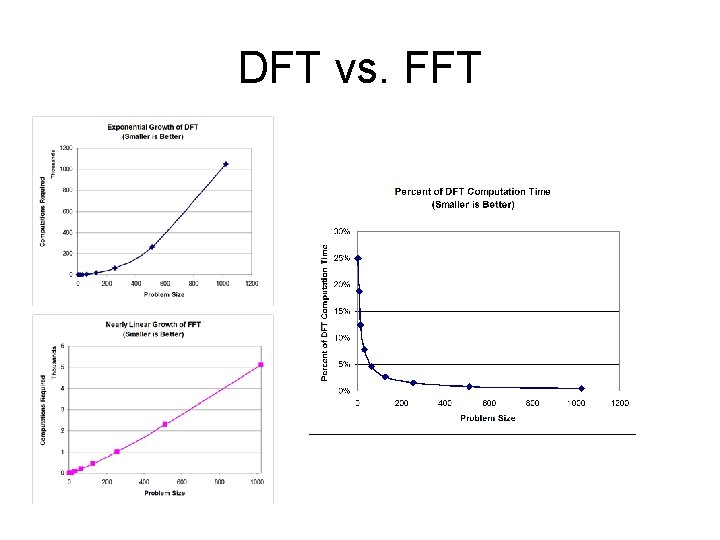
DFT vs. FFT

FFT Butterfly Operations • Butterfly arrangement of computations • Repeated on successive pairs of input data • Then half as many times on alternating pairs • Then half again as many times on every fourth element • …

The Butterfly • Simple operations repeated many times xe[n] X[n] Wn. N xo[n] X[n+N/2] -Wn. N

8 -point FFT Demonstration The Entire Calculation Output Input Array x[0] + + X[0] x[4] + + X[1] x[2] + + X[2] x[6] + + X[3] x[1] + + X[4] x[5] + + X[5] x[3] + + X[6] x[7] + + X[7] Multiplication by W factor + Addition

8 -point FFT Demonstration Input Array Output x[0] + + X[0] x[4] + + X[1] x[2] + + X[2] x[6] + + X[3] x[1] + + X[4] x[5] + + X[5] x[3] + + X[6] x[7] + + X[7] Multiplication by W factor + Addition

Why Hardware? • Even more speed for FFT • Extremely parallelizable • A whole layer can be done in two FPGA clock cycles – 1 multiply cycle – 1 add cycle – (Assuming sufficient multipliers)

Hardware Problems • • Complexity Input speed Output speed If the FPGA takes 24. 4 ns but takes 20 s to transfer the input data, what gain is there? – i. e. 24. 4 ns + 20 s = ~40 s!

Mitigation of Hardware Problems – Use a faster bus • AMD Opteron’s Hypertransport – 20. 8 GB/s (166. 4 Gb/s) per Link (V. 3) – Modules that fit into an AMD 64 -bit Opteron Socket – http: //www. drccomputer. com/pages/modules. html - xilinx based module – http: //www. xtremedatainc. com/xd 1000_brief. h tml - altera based module

Mitigation of Hardware Problems – Put the FPGA on the die with the DSP • Need silicon vendor support • FPGA can access memory on a very wide bus (i. e. 128 bits per cycle) – Implement the entire project in FPGA • Time consuming to program • Possibly insufficient room on the FPGA

8 -point FFT Demonstration In Hardware Input Array Output x[0] + + X[0] x[4] + + X[1] x[2] + + X[2] x[6] + + X[3] x[1] + + X[4] x[5] + + X[5] x[3] + + X[6] x[7] + + X[7] Multiplication by W factor + Addition

Why Not Software? • Each butterfly must be done sequentially • Only slight parallelism enabled by a DSP like the Tiger. SHARC • Each Butterfly can be done in 2 cycles (after optimization).

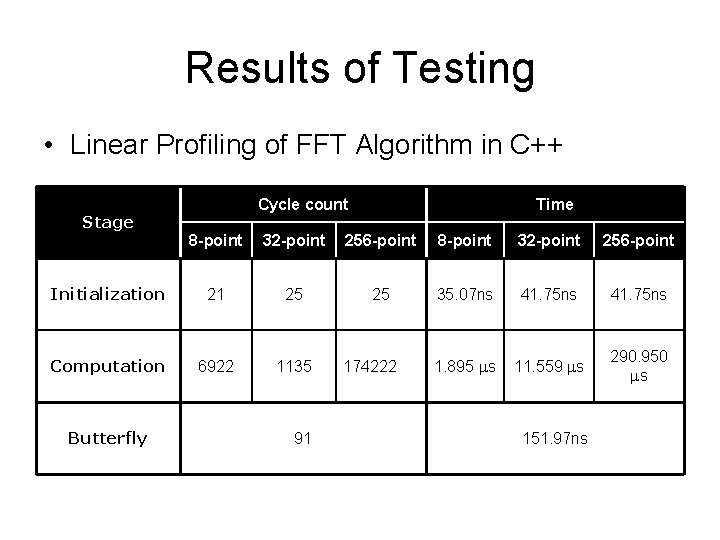
Results of Testing • Linear Profiling of FFT Algorithm in C++ Stage Cycle count Time 8 -point 32 -point 256 -point Initialization 21 25 25 35. 07 ns 41. 75 ns Computation 6922 1135 1. 895 s 11. 559 s 290. 950 s Butterfly 91 174222 151. 97 ns

Results of Testing • Profiling of VHDL on FPGA • Butterfly takes 24. 377 ns to execute – 62% is computational, 38% is routing on FPGA

Product Offerings • • Most DSP Vendors Many FPGA Vendors (IP – Intellectual Property) Microcontroller Vendors (i. e. Blackfin) FFTW – The Fastest Fourier Transform in the West • AMD Math Core Library • Intel Library • Highly Optimized for the expected hardware

Published Results • The Radix 4 version delivers a 1 K points complex processing time of 25 microseconds at 200 -MHz system speeds and uses only about 10 percent of the resources in a mid-range Stratix device. The Radix 2 is half the size of the Radix 4 and offers a 1 K points complex processing time of 50 microseconds at 200 MHz system speeds. Additional versions of the new cores are under development. [6] FFT IP Core Published Results [7] Texas Instruments C 6713 Single 4 DSP FFT core (Smaller is Better) Quad 4 DSP FFT core (Smaller is Better) 256 12. 3µs 3. 68µs 920 ns 512 27. 3µs 6. 24µs 1. 56µs 1024 60. 2µs 11. 4µs 2. 85µs FFT/IFFT length

References [1] Signals Systems and Transforms [2] James W. Cooley and John W. Tukey, "An algorithm for the machine calculation of complex Fourier series, " Math. Comput. 19, 297– 301 (1965). [3] http: //www. drccomputer. com/pages/modules. html - xilinx based module [4] http: //www. xtremedatainc. com/xd 1000_brief. html - altera based module [5] http: //www. amd. com/usen/Processors/Develop. With. AMD/0, , 30_2252_2353, 00. ht ml [6] http: //www. us. design-reuse. com/news 5650. html [7] http: //www. 4 dsp. com/fft. htm