Fermi Gas Model Heisenberg Uncertainty Principle Particle in

Fermi Gas Model

Heisenberg Uncertainty Principle Particle in dx will have a minimum uncertainty in px of dpx px dx Next particle in dx will have a momentum px Particles with px in dpx have minimum x-separation dx

Heisenberg Uncertainty Principle Identical conditions apply for the y, py, and z, pz -Therefore, in a fully degenerate system of fermions, (i. e. , all fermions in their lowest energy state), we have 1 particle in each 6 -dimensionl volume -- Phase space = volume Spatial Momentum volume

Heisenberg Uncertainty Principle In some d. Vps the maximum number d. N of unique quantum states (fermions) is pz p py px Number of states in a shell in p-space between p and p + dp Only Heisenberg uncertainty principle; completely general

FGM for the nucleus Treat protons & neutrons separately Consider a simple model for nucleus--

FGM for the nucleus Total energy eigenvalue degenerate eigenvalues unique states

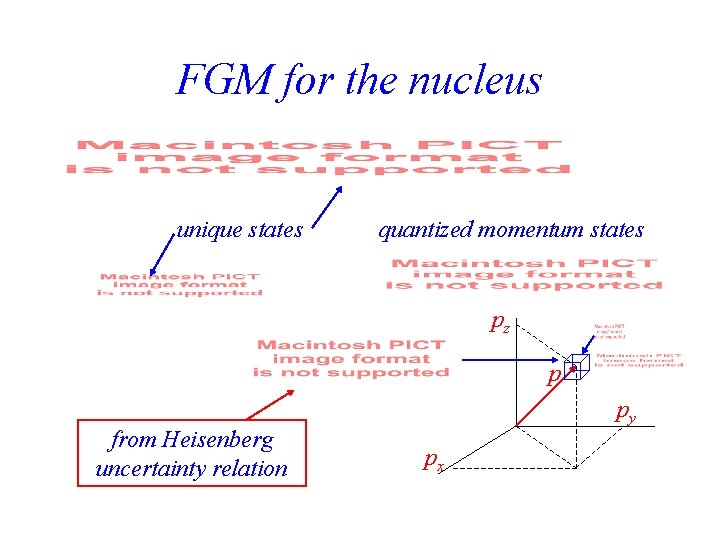
FGM for the nucleus unique states quantized momentum states pz p from Heisenberg uncertainty relation py px

FGM for the nucleus Assume extreme degeneracy all low levels filled up to a maximum -- called the Fermi level (EF) All momentum states up to p. F are filled (occupied) We want to estimate EF and p. F for nuclei -The number N of momentum states within the momentum-sphere up to p. F is -- p one p-state per dp 3 1/8 of sphere because nx, ny, nz > 0 pz py px

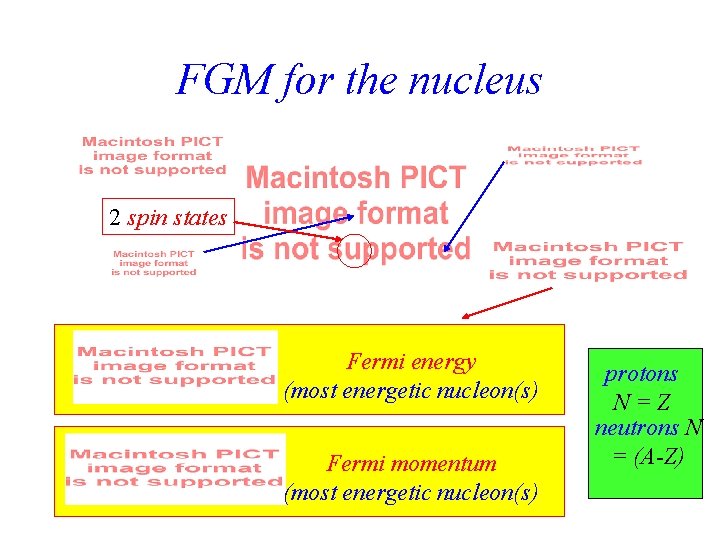
FGM for the nucleus 2 spin states Fermi energy (most energetic nucleon(s) Fermi momentum (most energetic nucleon(s) protons N=Z neutrons N = (A-Z)

FGM for the nucleus Protons Neutrons Assume Z = N

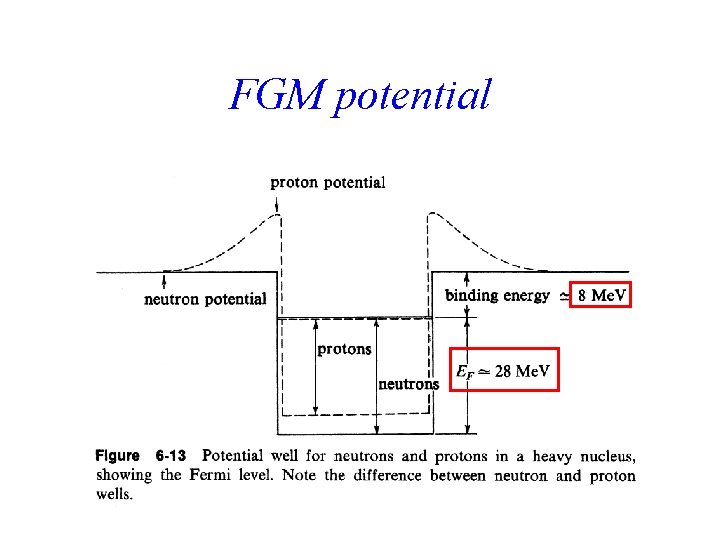
FGM potential

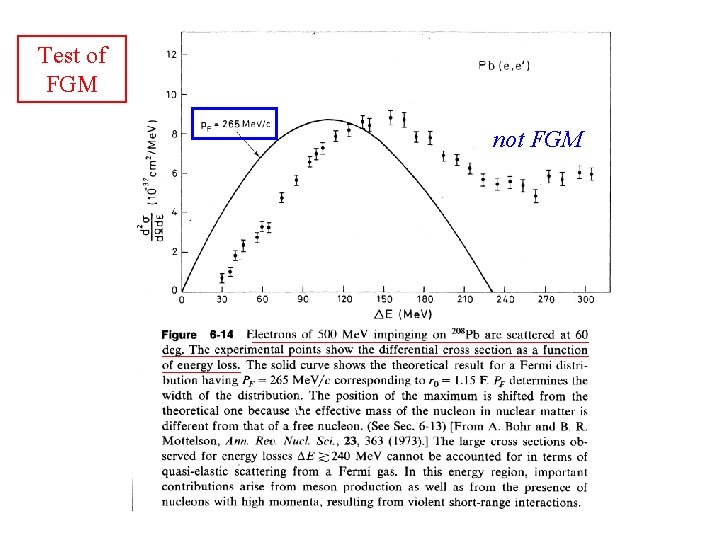
Test of FGM not FGM