Feedback Principles Analysis Dr John Choma Jr Professor

Feedback: Principles & Analysis Dr. John Choma, Jr. Professor of Electrical Engineering University of Southern California Department of Electrical Engineering-Electrophysics University Park; Mail Code: 0271 Los Angeles, California 90089 -0271 213 -740 -4692 [OFF] 626 -915 -7503 [HOME] 626 -915 -0944 [FAX] johnc@almaak. usc. edu (E-MAIL) EE 448 Feedback Principles & Analysis Fall 2001

Overview Of Lecture • Feedback § System Representation § System Analysis • High Frequency Dynamics § Open And Closed Loop Damping Factor § Open And Closed Loop Undamped Natural Frequency § Frequency Response §Phase Margin • High Speed Transient Dynamics § § Step Response Rise Time Settling Time Overshoot 65

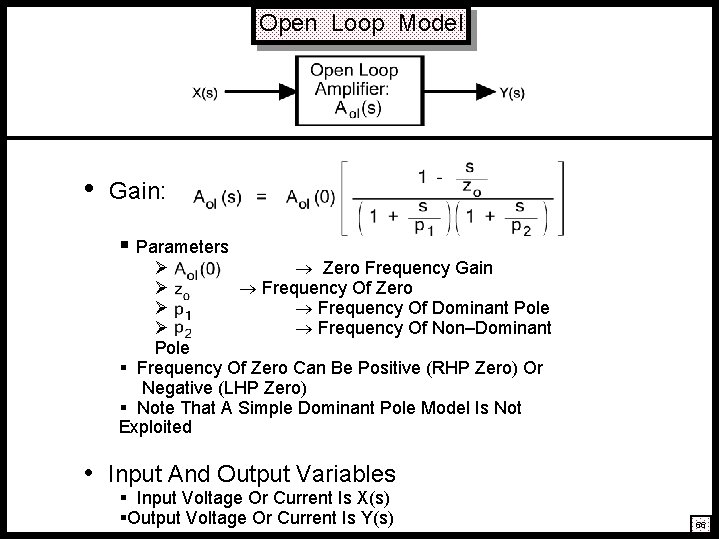
Open Loop Model • Gain: § Parameters Ø Zero Frequency Gain Ø Frequency Of Zero Ø Frequency Of Dominant Pole Ø Frequency Of Non–Dominant Pole § Frequency Of Zero Can Be Positive (RHP Zero) Or Negative (LHP Zero) § Note That A Simple Dominant Pole Model Is Not Exploited • Input And Output Variables § Input Voltage Or Current Is X(s) §Output Voltage Or Current Is Y(s) 663

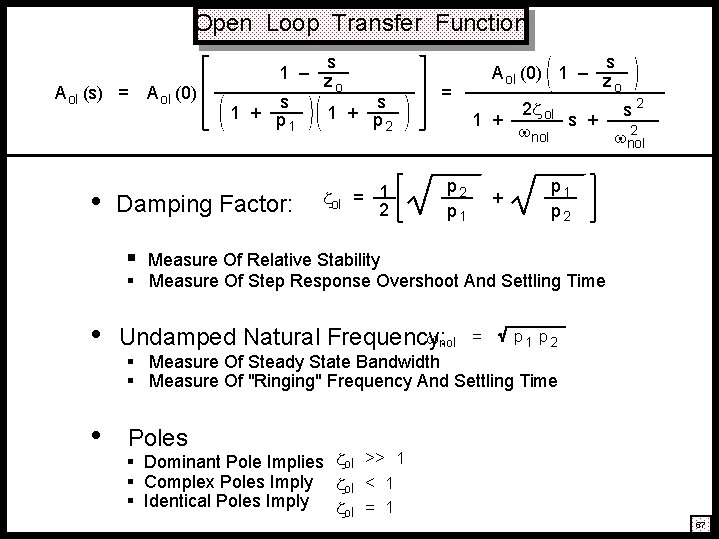
Open Loop Transfer Function A ol (s) = • A ol (0) s 1 – z o s s 1 + p 1 2 Damping Factor: ol = 1 2 = s A ol (0) 1 – z o 2 ol s 2 1 + s + 2 nol p 2 p 1 + p 1 p 2 § Measure Of Relative Stability § Measure Of Step Response Overshoot And Settling Time • • nol Undamped Natural Frequency: = p 1 p 2 § Measure Of Steady State Bandwidth § Measure Of "Ringing" Frequency And Settling Time Poles § Dominant Pole Implies ol >> 1 § Complex Poles Imply ol < 1 § Identical Poles Imply = 1 ol 674

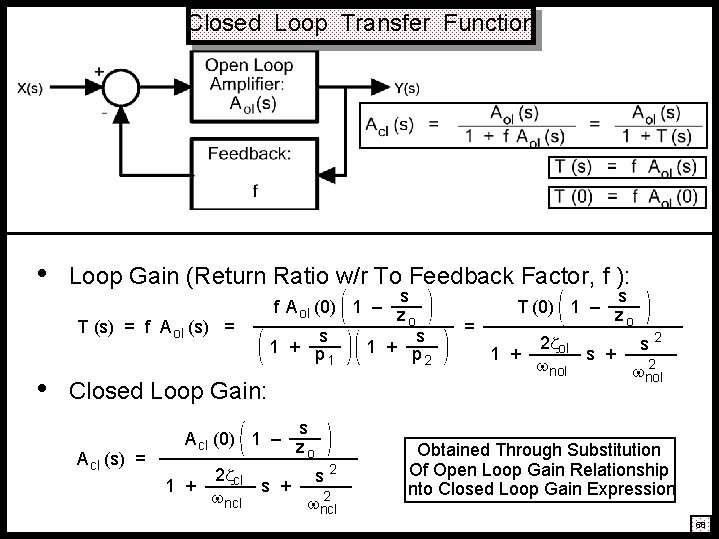
Closed Loop Transfer Function • Loop Gain (Return Ratio w/r To Feedback Factor, f ): T (s) = f A ol (s) = • s f A ol (0) 1 – z o s s 1 + p 1 2 Closed Loop Gain: A cl (s) = s A cl (0) 1 – z o 2 cl s 2 1 + s + 2 ncl = s T (0) 1 – z o 2 ol s 2 1 + s + 2 nol Obtained Through Substitution Of Open Loop Gain Relationship Into Closed Loop Gain Expression 68

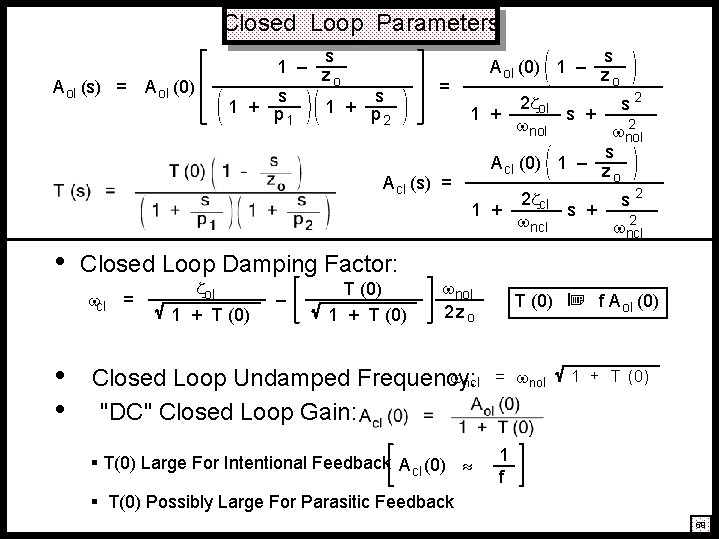
Closed Loop Parameters A ol (s) = A ol (0) s 1 – z o s s 1 + p 1 2 = A cl (s) = • Closed Loop Damping Factor: • • ol 1 + T (0) – T (0) 1 + T (0) 2 ol s 2 1 + s + 2 nol s A cl (0) 1 – z o 2 cl s 2 1 + s + 2 ncl nol 2 zo T (0) ncl Closed Loop Undamped Frequency: "DC" Closed Loop Gain: = nol § T(0) Large For Intentional Feedback A cl (0) 1 f cl = s A ol (0) 1 – z o f A ol (0) 1 + T (0) § T(0) Possibly Large For Parasitic Feedback 69

Closed Loop General Comments cl = • – T (0) 1 + T (0) nol 2 zo ncl = nol 1 + T (0) Damping Factor § Potential Instability Increases With Diminishing Damping Factor § Potential Instability Strongly Aggravated By Large Loop Gain § • ol 1 + T (0) Ø Note: Open Loop Damping Attenuation By Factor Of Square Root Of One Plus "DC" Loop Gain Ø For Intentional Feedback Having Closed Loop Gain Of (1/f ), Worst Case Is Unity Gain (f = 1), Corresponding To Maximal T(0) Open Loop Zero Ø Closed Loop Damping Diminished, Thus Potential Instability Aggravated, For Right Half Plane Open Loop Zero Ø Closed Loop Damping Increased, Thus Potential Instability Diminished, For Left Half Plane Open Loop Zero Undamped Frequency § Measure Of Closed Loop Bandwidth § Closed Loop Bandwidth Increases By Square Root Of One Plus "DC" Loop Gain, In Contrast To Increase By One Plus "DC" Loop Gain Predicted By Dominant Pole Analysis 70

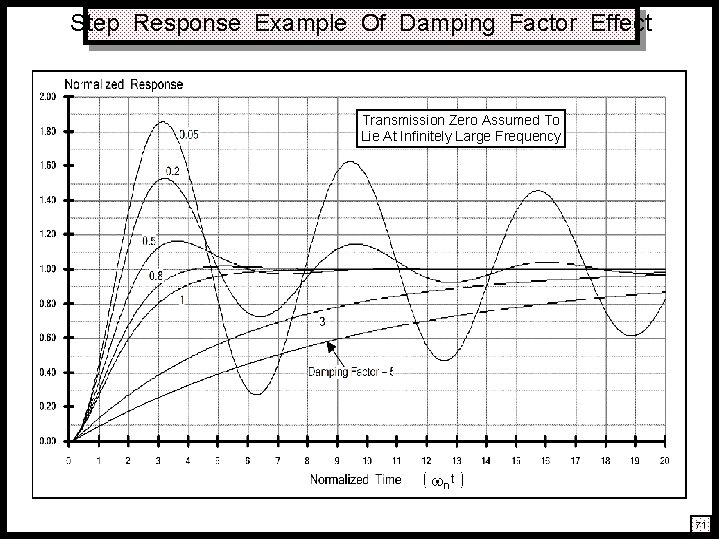
Step Response Example Of Damping Factor Effect Transmission Zero Assumed To Lie At Infinitely Large Frequency n t 71

Phase Margin (v ) = – tan • zo – tan p 1 – tan – 1 p 2 Unity Loop Gain Frequency § u T(0) p 1 § Assumes Frequencies Of Zero And Second Pole Are Larger Than u kpko – 1 Substitutions: p 2 = k p u z o = k o u k kp + ko Phase Margin § Difference Between Actual Loop Gain Phase Angle And – 180 ; • • – 1 A Safety Margin For Closed Loop Stability § Approximate Phase Margin: m tan § Since § Result Is Meaningful Only For k o – 1 1 + k T(0) – k tan – 1 (k) Can Be Negative, k Can Be A Negative Number kp > 1 72

Phase Margin Characteristic 120 Phase Margin (deg. ) 100 T(0) = 1 80 60 T(0) = 5 40 20 T(0) = 100 0 -1 -0. 8 -0. 6 -0. 4 -0. 2 0 -20 k 0. 2 0. 4 0. 6 0. 8 1 1. 2 1. 4 1. 6 1. 8 2 2. 4 2. 6 2. 8 3 -40 -60 73

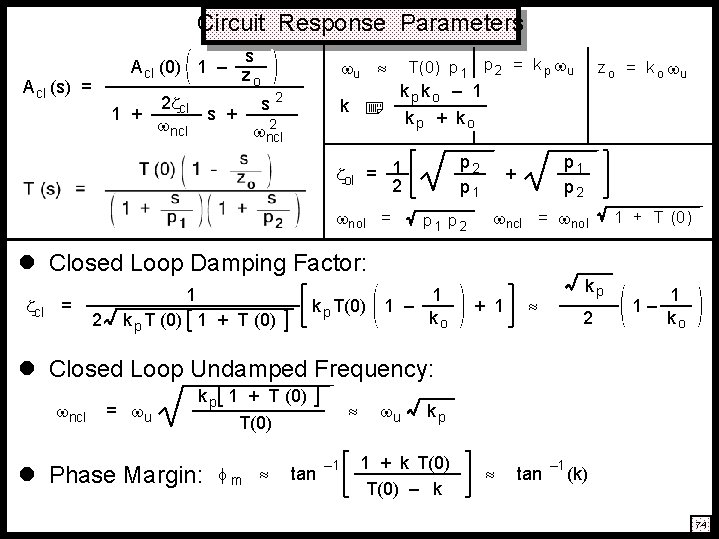
Circuit Response Parameters s A cl (0) 1 – z o 2 cl s 2 1 + s + 2 ncl k A cl (s) = T(0) p 1 p 2 = k p u u kpko – 1 kp + ko p 2 p 1 ol = 1 2 nol = p 1 p 2 + ncl = nol l Closed Loop Damping Factor: cl = 1 2 k p T(0) k p T (0) 1 + T (0) z o = k o u 1 1 – ko + 1 tan kp 2 1 + T (0) 1– 1 ko l Closed Loop Undamped Frequency: ncl = u k p 1 + T (0) T(0) l Phase Margin: m tan – 1 u kp 1 + k T(0) – k – 1 (k) 74

Closed Loop Example Calculation • Given: • Desire Maximally Flat Closed Loop Response, > 1/ Which cl Implies • Computations: kp cl § 2 k pk o – 1 kp + ko k = § • 1– 2 1 ko § m tan k p > 3. 125 k = 1. 8 Requisite Phase + k T(0) – 1 1 Margin: f 1 2 T(0) – k f m 63. 28 § In Practical Electronics, Phase Margins In The 60 s Of Degrees Are Usually Mandated, Which Requires That The Non. Dominant 75

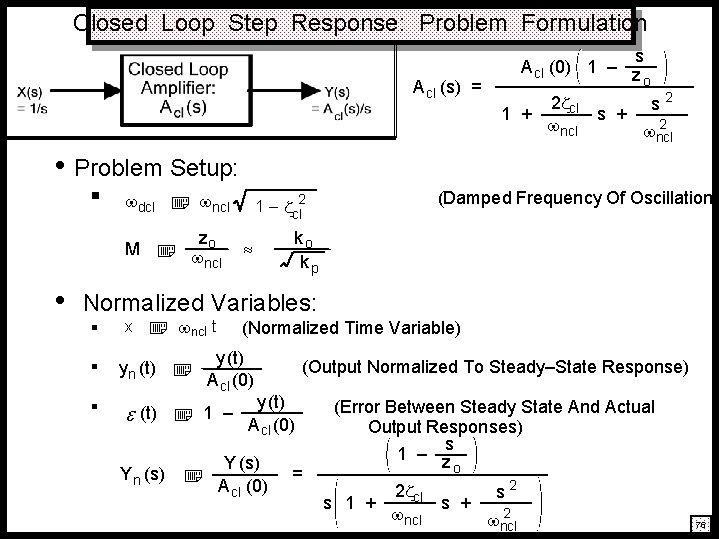
Closed Loop Step Response: Problem Formulation A cl (s) = s A cl (0) 1 – z o 2 cl s 2 1 + s + 2 ncl • Problem Setup: dcl • M § ncl zo ncl 1 – cl 2 (Damped Frequency Of Oscillation) ko kp Normalized Variables: x § § (t) 1 – Y n (s) y (t) A cl (0) yn (t) (Normalized Time Variable) § ncl t (Output Normalized To Steady–State Response) y (t) A cl (0) Y (s) A cl (0) = (Error Between Steady State And Actual Output Responses) s 1 – z o 2 cl s 2 s 1 + s + 2 ncl 76

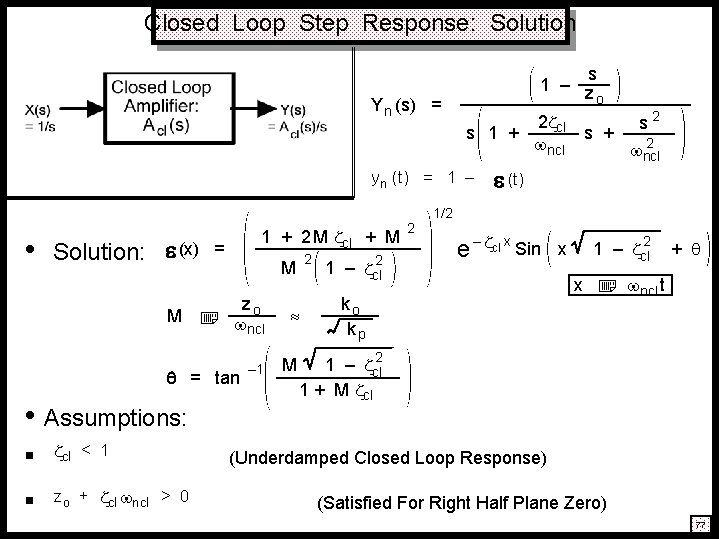
Closed Loop Step Response: Solution Y n (s) = s 1 – z o 2 cl s 2 s 1 + s + 2 ncl y n (t) = 1 – • Solution: (x) = M zo ncl – 1 M = tan • Assumptions: § cl < 1 § zo + cl ncl > 0 2 1 – 2 cl 2 1/2 e – cl x Sin ko kp 1 – cl 2 x x M 1 + 2 M cl + M (t) + ncl t 1 – cl 2 1 + M cl (Underdamped Closed Loop Response) (Satisfied For Right Half Plane Zero) 77

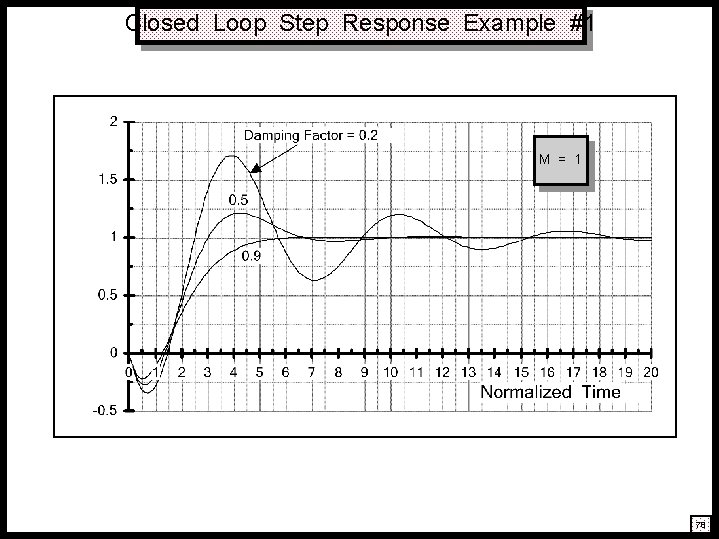
Closed Loop Step Response Example #1 M = 1 78

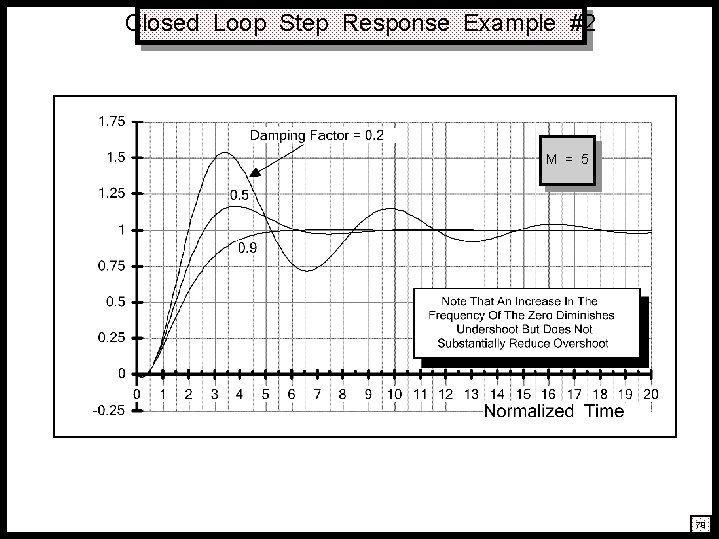
Closed Loop Step Response Example #2 M = 5 79

Closed Loop Settling Time (x) = 1 + 2 M cl + M M 2 1 – • Observations • Procedure § § § 2 cl 2 1/2 e – cl x Sin x 1 – cl 2 + y n (x) = 1 – (x) Magnitude Of Error Term Decreases Monotonically With x Maxima Of Error Determined By Setting Derivative Of Error Term With Respect To x To Zero Maxima Are Periodic With Period First Maximum Of Error Establishes Undershoot Point Determine Second Maximum And Constrain To Desired Minimal Error § Let Be The Normalized Time Corresponding To Second Error Maximum m § Let m Be The Magnitude Of Error Correspondingx. To xm § If m Is The Desired Settling Error, Represents The Settling Time Of the Circuit 80

Closed Loop Settling Time Results (x) = 1 + 2 M cl + M M 2 1 – 2 1/2 2 cl e – cl x Sin y n (x) = 1 – • Results: xm m • 1 = – cl 2 1 – cl 2 x + (x) + tan 2 1 + 2 M cl + M M 1 – cl 2 cl + M – 1 – x e cl m For Large M (Far Right Half Plane Zero): xm m 1 – cl 2 exp – 2 4 – kp kp 4 – kp 81

Closed Loop Settling Time Example • Requirements • Computations § Settling To Within One Percent In 1 n. SEC § Assume Zero Is In Far Right Half Plane (Reasonable Approximation For Common Gate And Compensated Source Follower; First Order Approximation For Common Source) § Assume Very Large "DC" Loop Gain § m exp – kp 0. 01 k p > 2. 73 ; 4 – kp Second Pole Must Be At Least 2. 7 Times Larger Than Unity Gain Frequency § 2 4 – kp x m = ncl t m ncl u kp = 5. 575 ncl 2 (887. 2 MHz) ; u 2 (537 MHz) § Required Phase Margin: f m tan – 1 (k p ) = 69. 9 82