Feedback Control Systems Lecture 8 Dr Ing Erwin

Feedback Control Systems Lecture 8 Dr. -Ing. Erwin Sitompul President University http: //zitompul. wordpress. com 2 0 2 1 President University Erwin Sitompul FCS 8/1

Feedback Control Systems Chapter 5 The Root-Locus Design Method President University Erwin Sitompul FCS 8/2

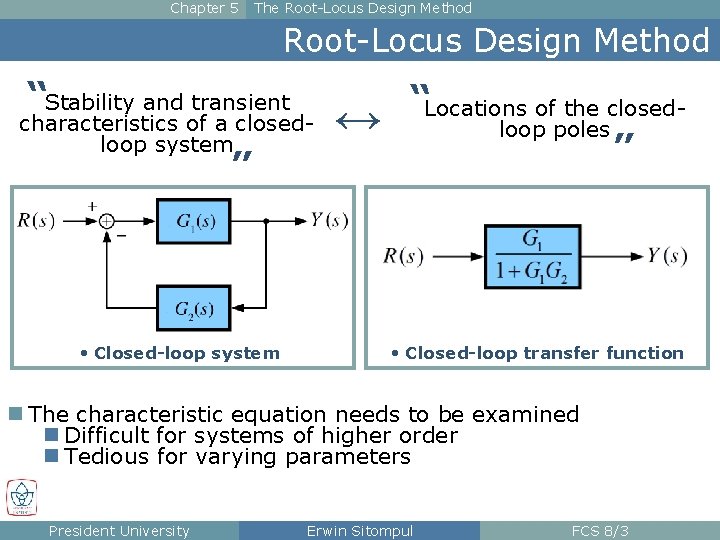
Chapter 5 The Root-Locus Design Method “Stability and transient characteristics of a closedloop system ” • Closed-loop system ↔ “Locations of the closedloop poles ” • Closed-loop transfer function n The characteristic equation needs to be examined n Difficult for systems of higher order n Tedious for varying parameters President University Erwin Sitompul FCS 8/3

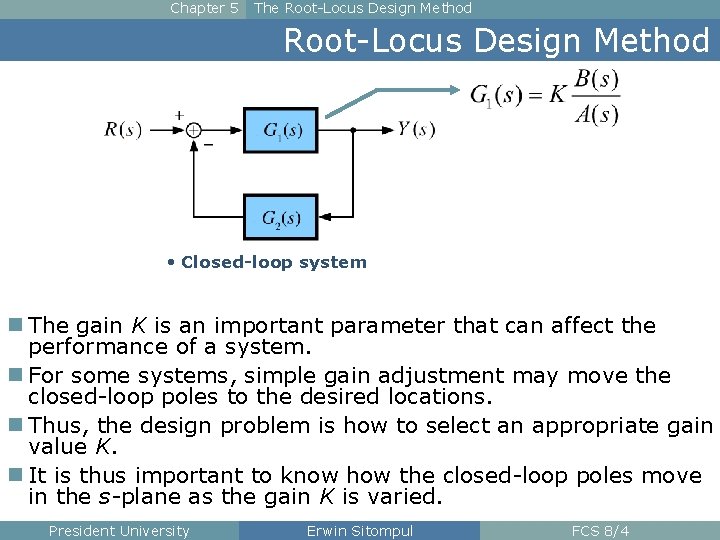
Chapter 5 The Root-Locus Design Method • Closed-loop system n The gain K is an important parameter that can affect the performance of a system. n For some systems, simple gain adjustment may move the closed-loop poles to the desired locations. n Thus, the design problem is how to select an appropriate gain value K. n It is thus important to know how the closed-loop poles move in the s-plane as the gain K is varied. President University Erwin Sitompul FCS 8/4

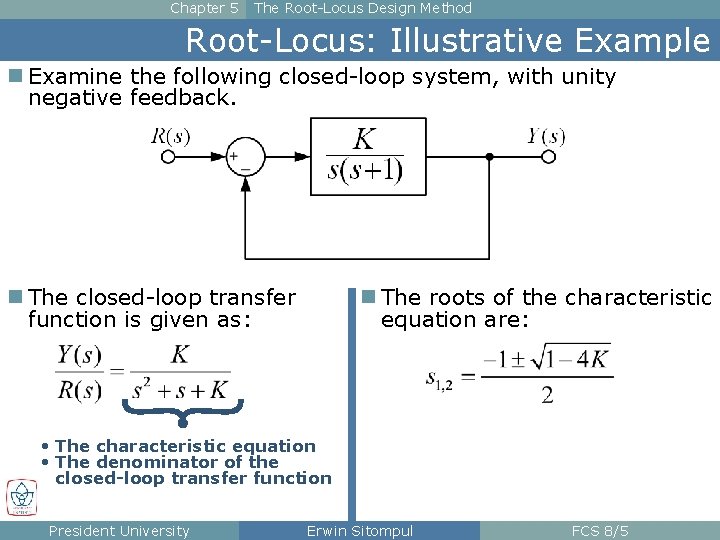
Chapter 5 The Root-Locus Design Method Root-Locus: Illustrative Example n Examine the following closed-loop system, with unity negative feedback. n The closed-loop transfer function is given as: n The roots of the characteristic equation are: • The characteristic equation • The denominator of the closed-loop transfer function President University Erwin Sitompul FCS 8/5

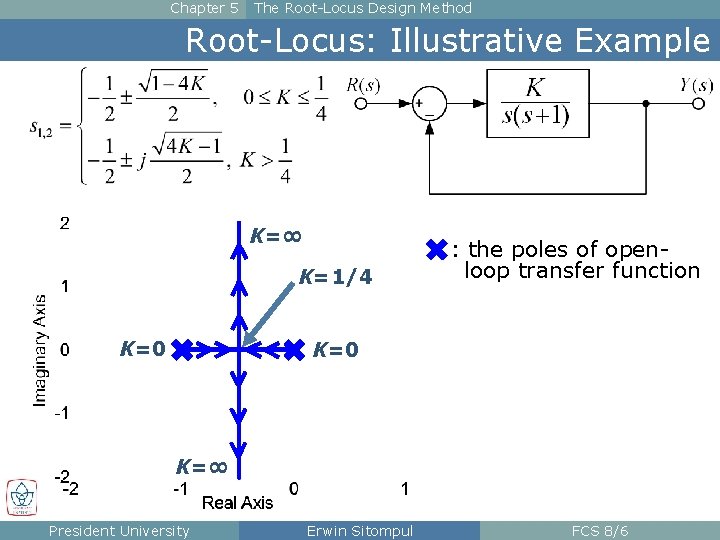
Chapter 5 The Root-Locus Design Method Root-Locus: Illustrative Example K=∞ K=1/4 K=0 : the poles of openloop transfer function K=0 K=∞ President University Erwin Sitompul FCS 8/6

Chapter 5 The Root-Locus Design Method Root-Locus: Illustrative Example n Where are the location of the closed-loop roots when K=1? K=1 – 0. 5 President University 0. 866 – 0. 866 There is a relation between gain K and the position of closed-loop poles, which also affects the dynamic properties of the system (ζ and ωd). Erwin Sitompul FCS 8/7

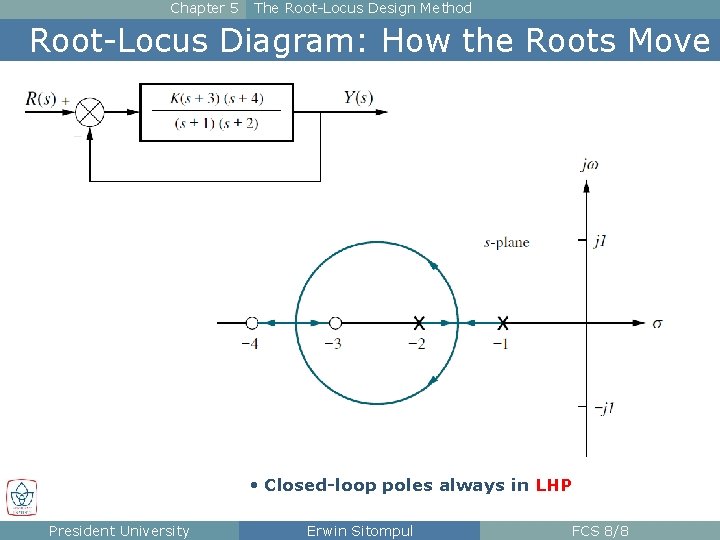
Chapter 5 The Root-Locus Design Method Root-Locus Diagram: How the Roots Move • Closed-loop poles always in LHP President University Erwin Sitompul FCS 8/8

Chapter 5 The Root-Locus Design Method Root-Locus Diagram: How the Roots Move • Closed-loop poles will crossover to RHP if gain is increased President University Erwin Sitompul FCS 8/9

Chapter 5 The Root-Locus Design Method Root-Locus of a Basic Feedback System n The closed-loop transfer function of the basic feedback system above is: n The characteristic equation, whose roots are the poles of this transfer function, is: President University Erwin Sitompul FCS 8/10

Chapter 5 The Root-Locus Design Method Root-Locus of a Basic Feedback System n To put the characteristic equation in a form suitable for study of the roots as a parameter changes, it is rewritten as: where n K is the gain of controller-plant-sensor combination. n K is selected as the parameter of interest. n W. R. Evans (in 1948, at the age of 28) suggested to plot the locus (location) of all possible roots of the characteristic equation as K varies from zero to infinity Root-Locus plot. n The resulting plot is to be used as an aid in selecting the best value of K. President University Erwin Sitompul FCS 8/11

Chapter 5 The Root-Locus Design Method Root-Locus of a Basic Feedback System n The Root-Locus problem shall now be expressed in several equivalent but useful ways. n The equations above are sometimes referred to as “the Root. Locus form of a characteristic equation. ” n The Root-Locus is the set of values of s for which the above equations hold for some positive real value of K. President University Erwin Sitompul FCS 8/12

Chapter 5 The Root-Locus Design Method Root-Locus of a Basic Feedback System n Explicit solutions are difficult to obtain for higher-order system General rules for the construction of a Root-Locus were developed by Evans. n With the availability of MATLAB, plotting a Root-Locus becomes very easy. It can be done simply by using the command “rlocus(num, den)” and “rlocfind(num, den)”. n However, in control design we are also interested in how to modify the dynamic response so that a system can meet the specifications for good control performance. n For this purpose, it is very useful to be able to roughly sketch a Root-Locus which will be used to examine a system and to evaluate the consequences of possible compensation alternatives. n Also, it is important to be able to quickly evaluate the correctness of a MATLAB-generated locus to verify that what is plotted is in fact what was meant to be plotted. President University Erwin Sitompul FCS 8/13

Chapter 5 The Root-Locus Design Method Guidelines for Sketching a Human Face President University Erwin Sitompul FCS 8/14

Chapter 5 The Root-Locus Design Method Guideines for Sketching a Root-Locus n Deriving using the Root-Locus form of characteristic equation, n Taking the polynomial a(s) and b(s) to be monic, i. e. , the coefficient of the highest power of s equals 1, they can be factorized as: n If any s = s 0 fulfills the equation above, then s 0 is said to be on the Root-Locus. President University Erwin Sitompul FCS 8/15

Chapter 5 The Root-Locus Design Method Guideines for Sketching a Root-Locus n The magnitude condition implies: Magnitude Condition n The phase condition implies: Phase Condition n Defining and can be rewritten as: President University Erwin Sitompul , the phase condition FCS 8/16

Chapter 5 “ The Root-Locus Design Method Guideines for Sketching a Root-Locus The Root-Locus is the set of values of s for which 1 + KL(s) = 0 is satisfied as the real parameter K varies from 0 to ∞. Typically, 1 + KL(s) = 0 is the characteristic equation of the system, and in this case the roots on the locus are the closed-loop poles of that system. ” “ The Root-Locus of L(s) is the set of points in the splane where the phase of L(s) is 180°. If the angle to a test point from a zero is defined as ψi and the angle to a test point from a pole as Φi, then the Root-Locus of L(s) is expressed as those points in the s-plane where, for integer l, Σψi – ΣΦi = 180° + 360°(l– 1). ” President University Erwin Sitompul FCS 8/17

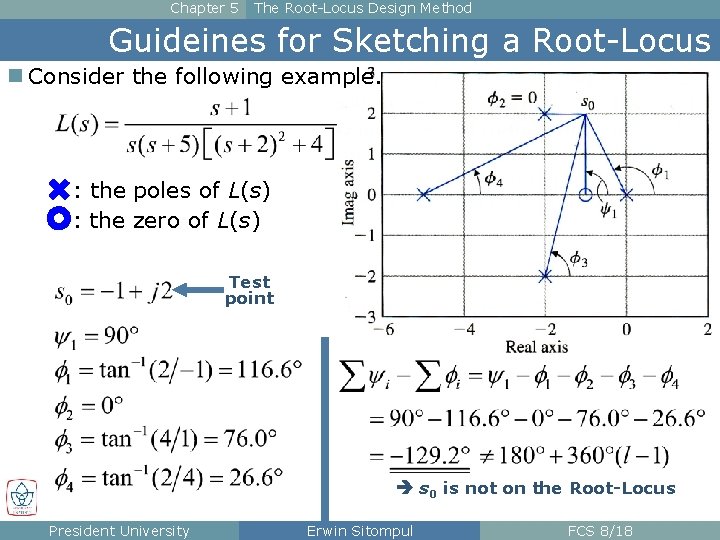
Chapter 5 The Root-Locus Design Method Guideines for Sketching a Root-Locus n Consider the following example. : the poles of L(s) : the zero of L(s) Test point s 0 is not on the Root-Locus President University Erwin Sitompul FCS 8/18

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus RULE 1: The n branches of the locus start at the poles of L(s) and m of these branches end on the zeros of L(s), while n–m branches terminate at infinity along asymptotes. Recollecting The Root-Locus starts at K = 0 at the poles of L(s) and ends at K = ∞ on the zeros of L(s) President University Erwin Sitompul FCS 8/19

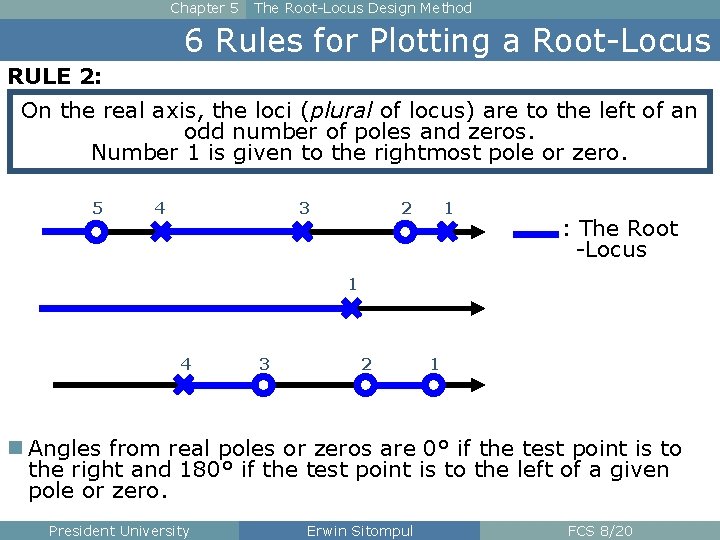
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus RULE 2: On the real axis, the loci (plural of locus) are to the left of an odd number of poles and zeros. Number 1 is given to the rightmost pole or zero. 5 4 3 2 1 : The Root -Locus 1 4 3 2 1 n Angles from real poles or zeros are 0° if the test point is to the right and 180° if the test point is to the left of a given pole or zero. President University Erwin Sitompul FCS 8/20

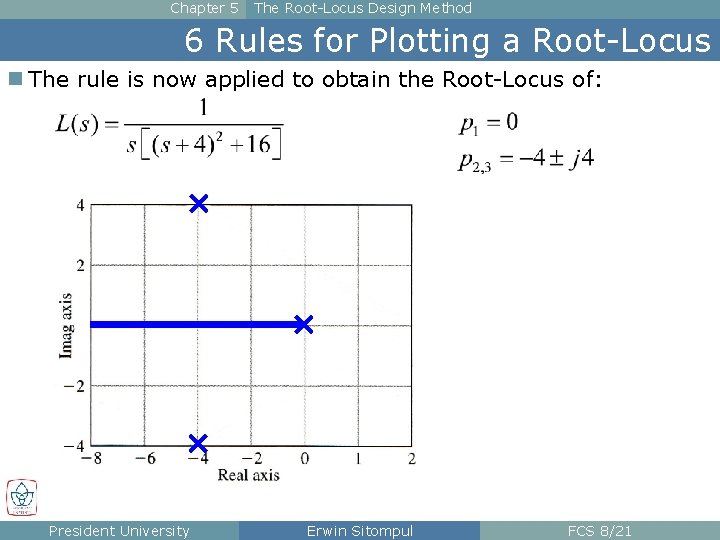
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n The rule is now applied to obtain the Root-Locus of: President University Erwin Sitompul FCS 8/21

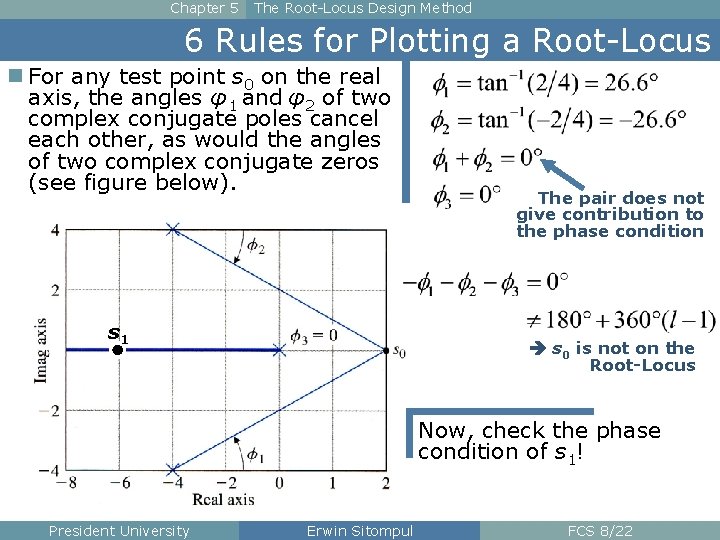
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n For any test point s 0 on the real axis, the angles φ1 and φ2 of two complex conjugate poles cancel each other, as would the angles of two complex conjugate zeros (see figure below). s 1 The pair does not give contribution to the phase condition s 0 is not on the Root-Locus Now, check the phase condition of s 1! President University Erwin Sitompul FCS 8/22

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus RULE 3: For large s and K, n–m of the loci are asymptotic to lines at angles Φl radiating out from the point s = a on the real axis, where: Angles of Asymptotes Center of Asymptotes President University Erwin Sitompul FCS 8/23

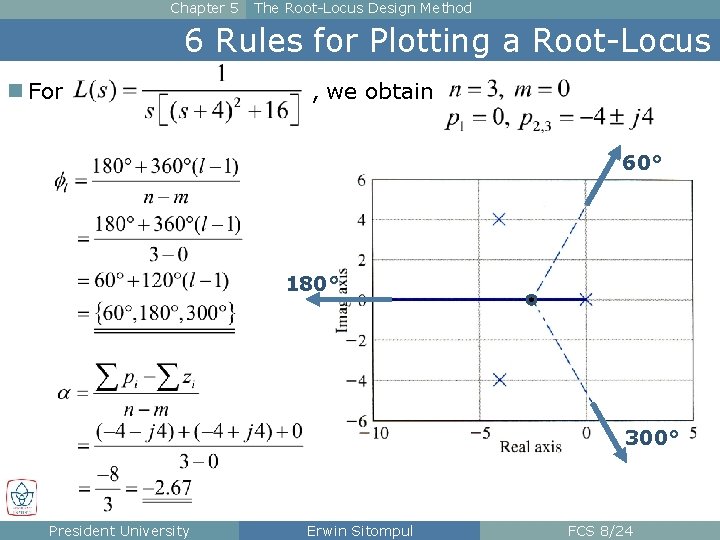
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n For , we obtain 60° 180° – 2. 67 300° President University Erwin Sitompul FCS 8/24

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus RULE 4: The angle of departure of a branch of a locus from a complex pole is given by: and the angle of arrival of a branch of a locus to a complex zero is given by: President University Erwin Sitompul FCS 8/25

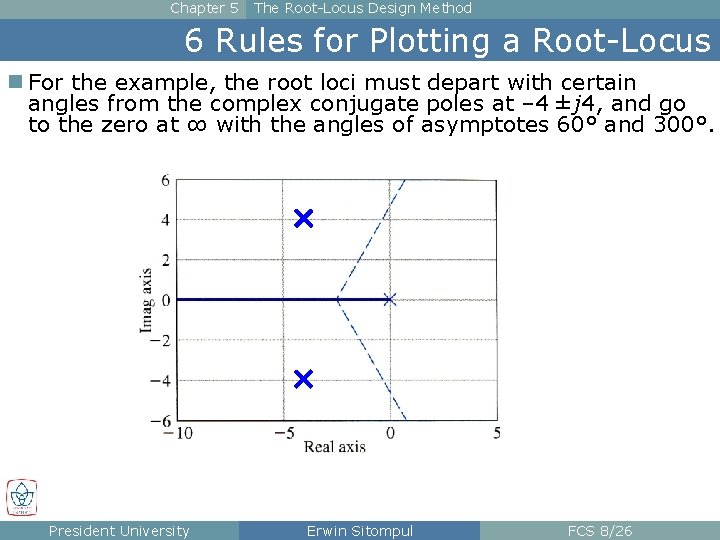
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n For the example, the root loci must depart with certain angles from the complex conjugate poles at – 4 ± j 4, and go to the zero at ∞ with the angles of asymptotes 60° and 300°. President University Erwin Sitompul FCS 8/26

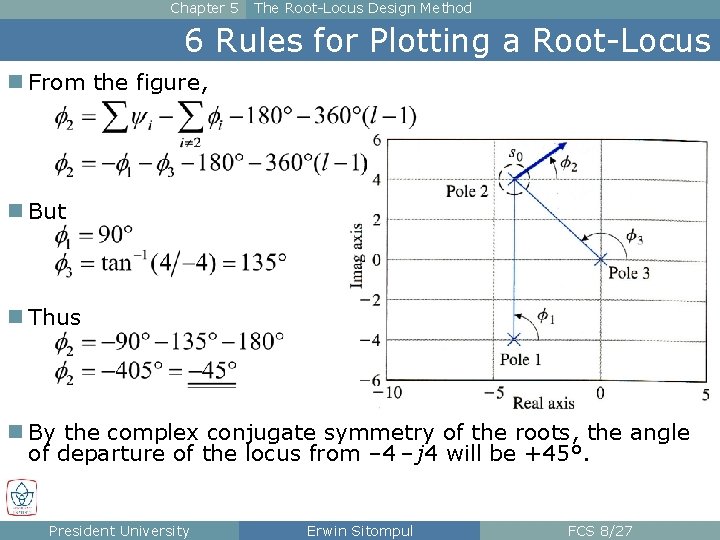
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n From the figure, n But n Thus n By the complex conjugate symmetry of the roots, the angle of departure of the locus from – 4 – j 4 will be +45°. President University Erwin Sitompul FCS 8/27

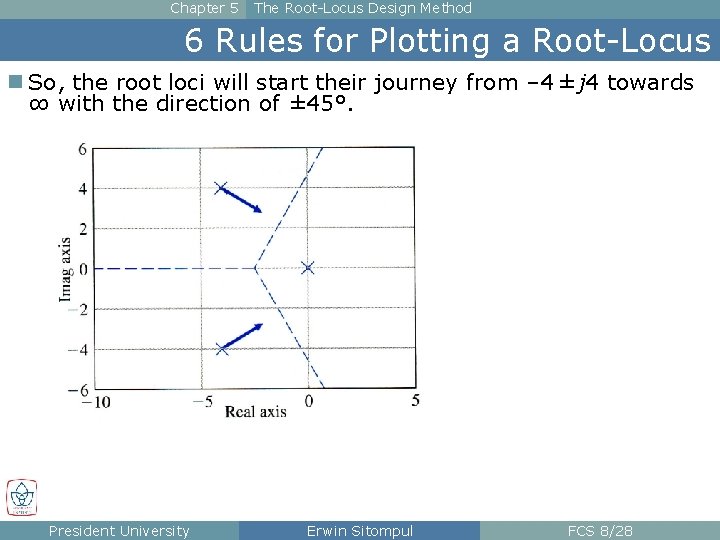
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n So, the root loci will start their journey from – 4 ± j 4 towards ∞ with the direction of ± 45°. President University Erwin Sitompul FCS 8/28

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus RULE 5: The locus crosses the jω axis (imaginary axis, border between LHP and RHP) at points where: n The Routh criterion shows a transition from roots in the left half-plane to roots in the right half-plane. n This transition means that the closed-loop system is becoming unstable. n This fact can be tested by Routh’s stability criterion, with K as the parameter, where an incremental change of K will cause the sign change of an element in the first column of Routh’s array. n The values of s = ± jω0 are the solution of the characteristic equation in Root-Locus form, 1 + KL(s) = 0. n The points ± jω0 are the points of cross-over on the imaginary axis. President University Erwin Sitompul FCS 8/29

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n For the example, the characteristic equation can be written as: • The closed-loop system is stable for K > 0 and K < 256 for 0 < K < 256. • For K > 256 there are 2 roots in the RHP (two sign changes in the first column). • For K = 256 the roots must be on the imaginary axis. President University Erwin Sitompul FCS 8/30

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n The characteristic equation is now solved using K = 256. Points of Cross-over n Another way to solve for ω0 is by simply replacing any s with jω0 without finding the value of K first. ≡ 0 President University ≡ 0 Same results for K and ω0 Erwin Sitompul FCS 8/31

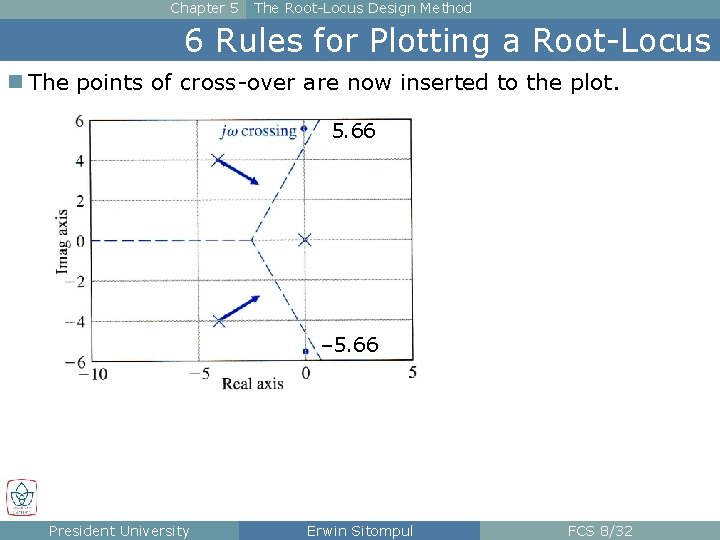
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n The points of cross-over are now inserted to the plot. 5. 66 – 5. 66 President University Erwin Sitompul FCS 8/32

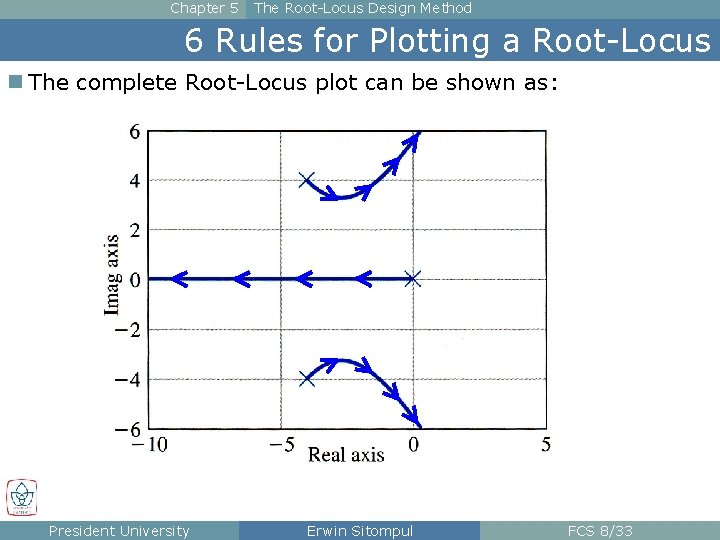
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n The complete Root-Locus plot can be shown as: President University Erwin Sitompul FCS 8/33

Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus RULE 6: The locus will have multiple roots at points (break-away or break-away points, on real axis) on the locus where: The branches will approach and depart a point of q roots at angles separated by: President University Erwin Sitompul FCS 8/34

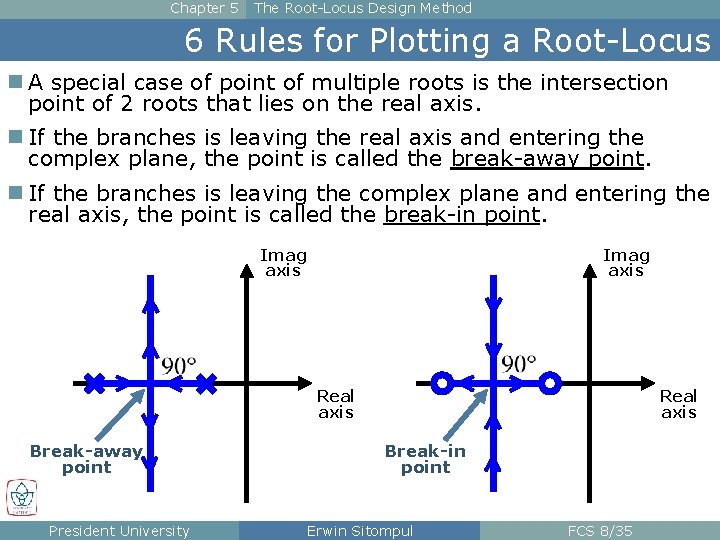
Chapter 5 The Root-Locus Design Method 6 Rules for Plotting a Root-Locus n A special case of point of multiple roots is the intersection point of 2 roots that lies on the real axis. n If the branches is leaving the real axis and entering the complex plane, the point is called the break-away point. n If the branches is leaving the complex plane and entering the real axis, the point is called the break-in point. Imag axis Real axis Break-away point President University Real axis Break-in point Erwin Sitompul FCS 8/35

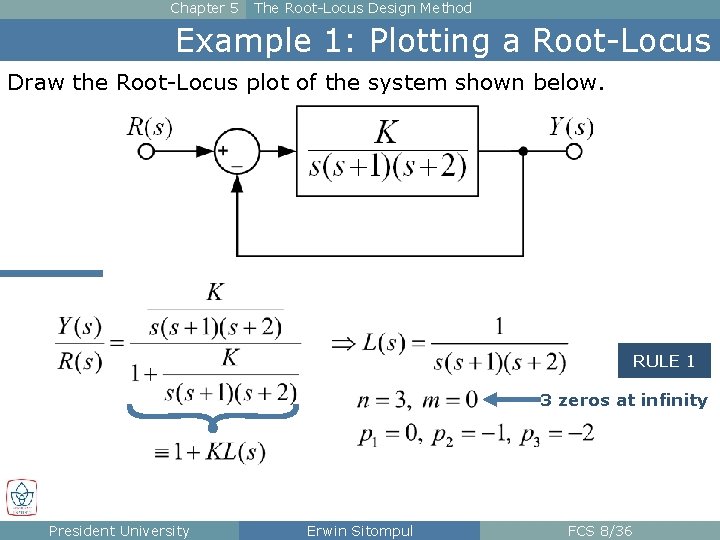
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus Draw the Root-Locus plot of the system shown below. RULE 1 3 zeros at infinity President University Erwin Sitompul FCS 8/36

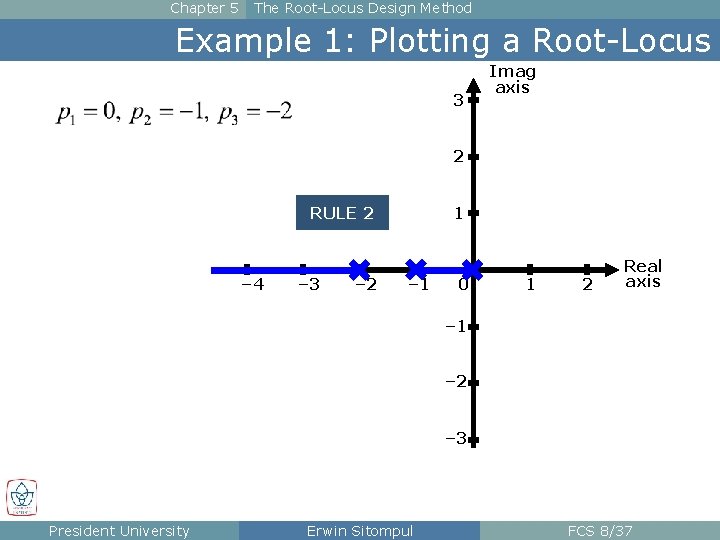
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus 3 Imag axis 2 1 RULE 2 – 4 – 3 – 2 – 1 0 1 2 Real axis – 1 – 2 – 3 President University Erwin Sitompul FCS 8/37

Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus Angles of Asymptotes Center of Asymptotes President University Erwin Sitompul FCS 8/38

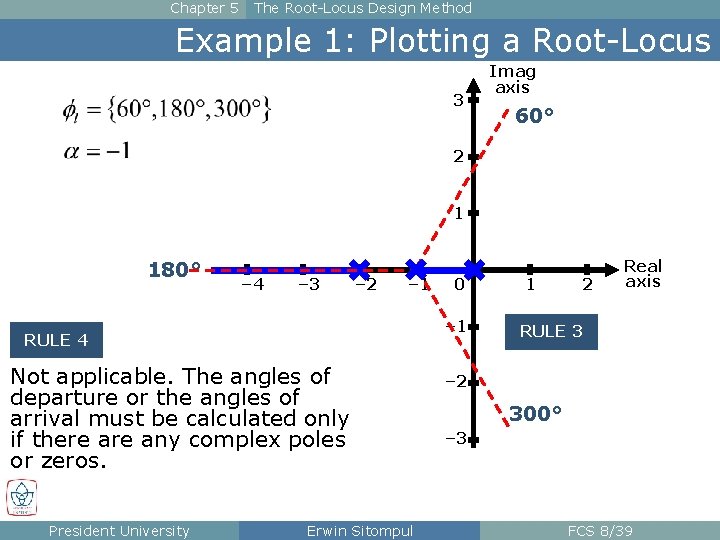
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus 3 Imag axis 60° 2 1 180° – 4 – 3 – 2 – 1 RULE 4 Not applicable. The angles of departure or the angles of arrival must be calculated only if there any complex poles or zeros. President University 0 Erwin Sitompul 1 2 Real axis RULE 3 – 2 300° – 3 FCS 8/39

Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus Replacing s with jω0, ≡ 0 President University ≡ 0 Points of Cross-over Erwin Sitompul FCS 8/40

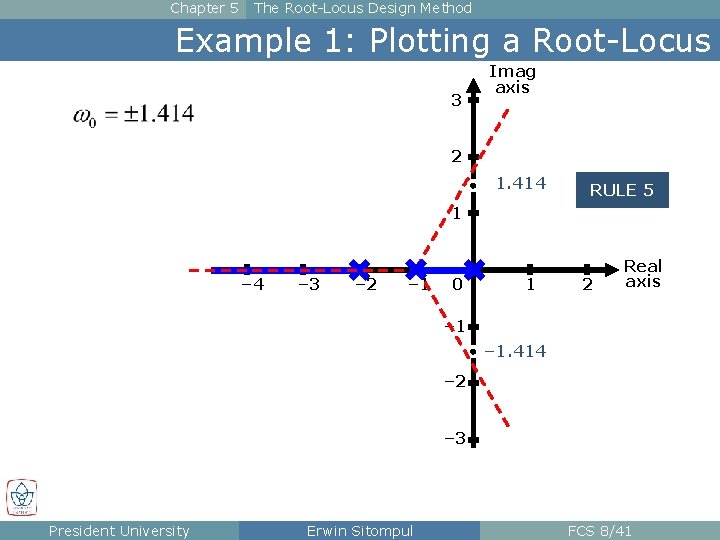
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus 3 Imag axis 2 1. 414 RULE 5 1 – 4 – 3 – 2 – 1 0 1 2 Real axis – 1. 414 – 2 – 3 President University Erwin Sitompul FCS 8/41

Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus The Root-Locus must have a break-away point on the real axis, between – 1 and 0. It can be found by solving: President University Erwin Sitompul FCS 8/42

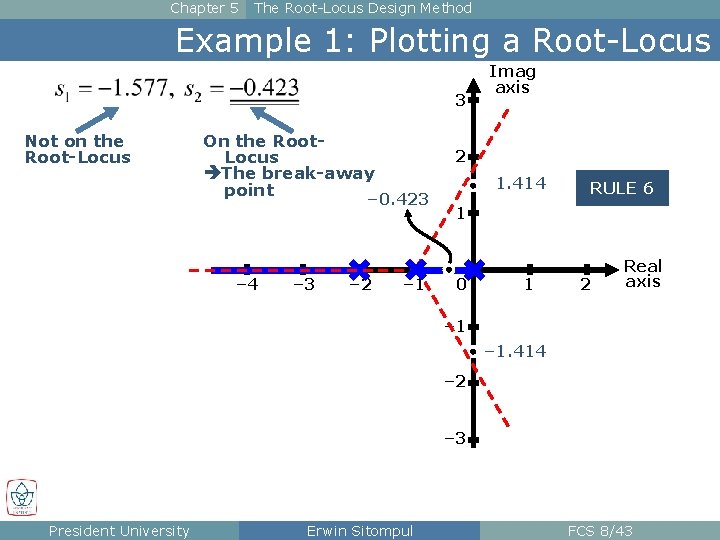
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus 3 Not on the Root-Locus On the Root. Locus The break-away point 2 – 0. 423 – 4 – 3 – 2 Imag axis – 1 1. 414 RULE 6 1 0 1 2 Real axis – 1. 414 – 2 – 3 President University Erwin Sitompul FCS 8/43

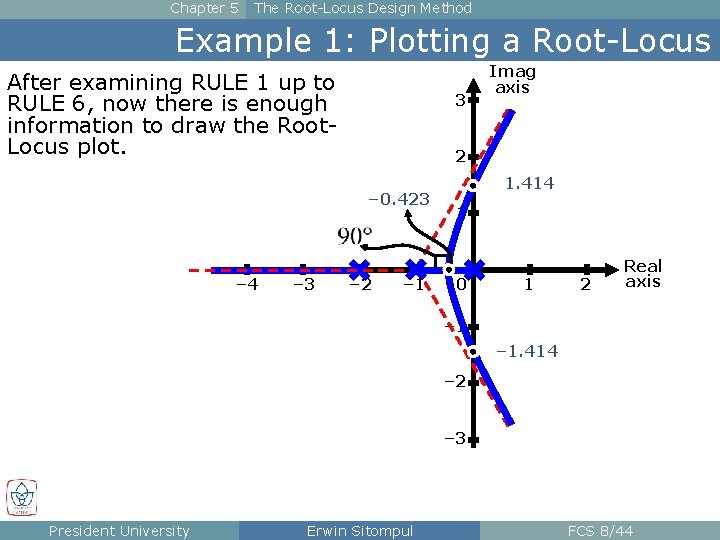
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus After examining RULE 1 up to RULE 6, now there is enough information to draw the Root. Locus plot. 3 2 – 0. 423 – 4 – 3 Imag axis – 2 – 1 1. 414 1 0 1 2 Real axis – 1. 414 – 2 – 3 President University Erwin Sitompul FCS 8/44

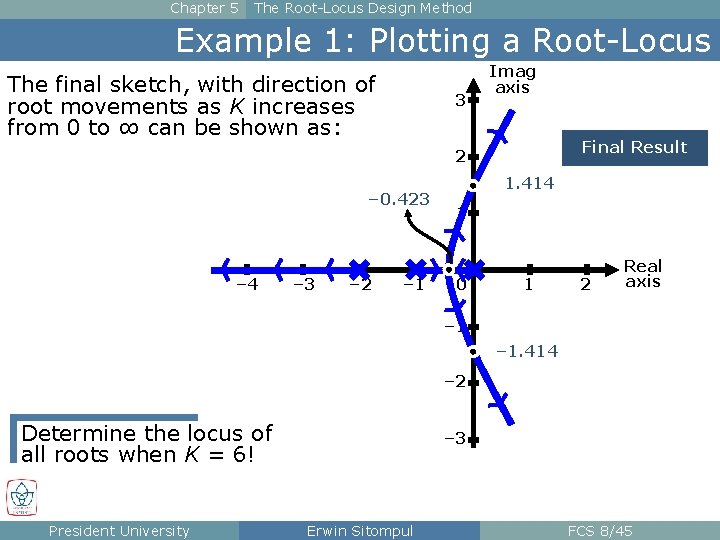
Chapter 5 The Root-Locus Design Method Example 1: Plotting a Root-Locus The final sketch, with direction of root movements as K increases from 0 to ∞ can be shown as: 3 Imag axis Final Result 2 – 0. 423 – 4 – 3 – 2 – 1 1. 414 1 0 1 2 Real axis – 1. 414 – 2 Determine the locus of all roots when K = 6! President University – 3 Erwin Sitompul FCS 8/45

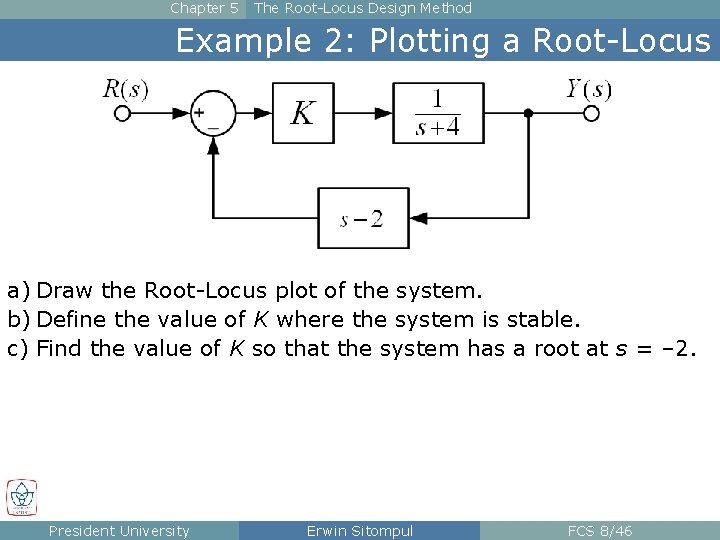
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus a) Draw the Root-Locus plot of the system. b) Define the value of K where the system is stable. c) Find the value of K so that the system has a root at s = – 2. President University Erwin Sitompul FCS 8/46

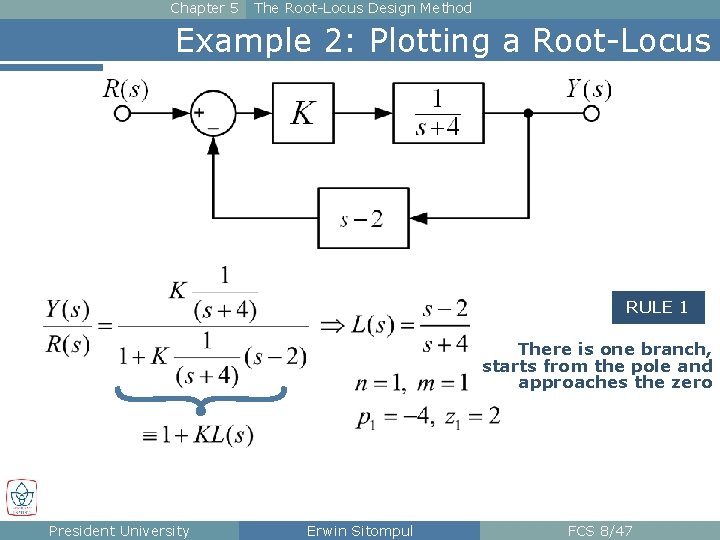
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus RULE 1 There is one branch, starts from the pole and approaches the zero President University Erwin Sitompul FCS 8/47

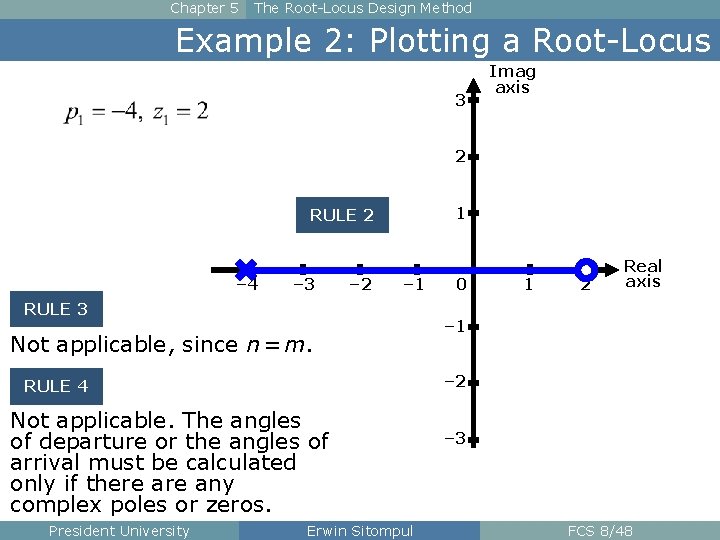
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus 3 Imag axis 2 1 RULE 2 – 4 – 3 – 2 – 1 RULE 3 Not applicable, since n = m. 1 2 – 1 – 2 RULE 4 Not applicable. The angles of departure or the angles of arrival must be calculated only if there any complex poles or zeros. President University 0 Real axis Erwin Sitompul – 3 FCS 8/48

Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus Replacing s with jω0, ≡ 0 President University ≡ 0 Points of Cross-over Erwin Sitompul FCS 8/49

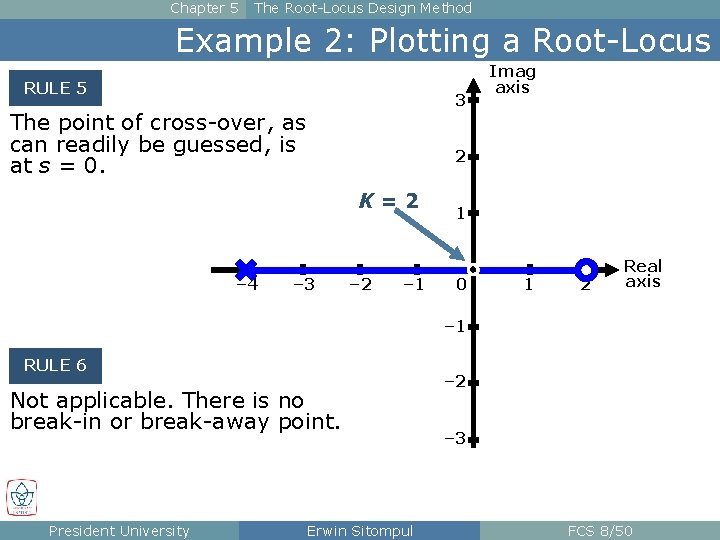
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus RULE 5 3 The point of cross-over, as can readily be guessed, is at s = 0. 2 K=2 – 4 Imag axis – 3 – 2 – 1 1 0 1 2 Real axis – 1 RULE 6 Not applicable. There is no break-in or break-away point. President University Erwin Sitompul – 2 – 3 FCS 8/50

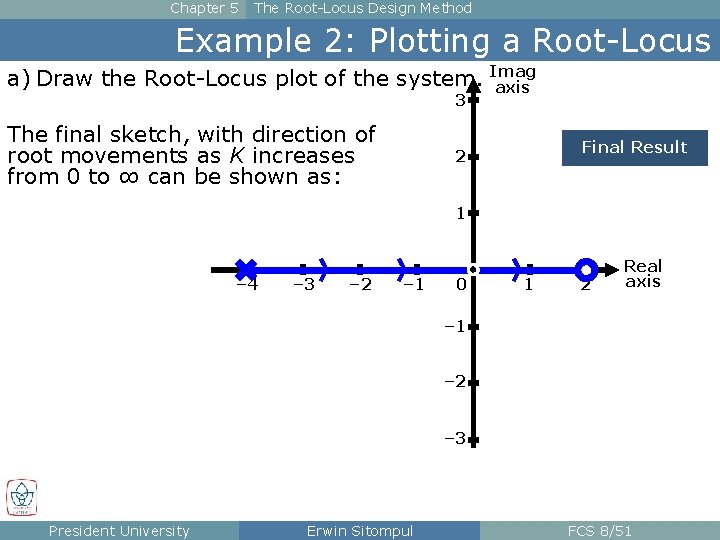
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus a) Draw the Root-Locus plot of the system. Imag axis 3 The final sketch, with direction of root movements as K increases from 0 to ∞ can be shown as: Final Result 2 1 – 4 – 3 – 2 – 1 0 1 2 Real axis – 1 – 2 – 3 President University Erwin Sitompul FCS 8/51

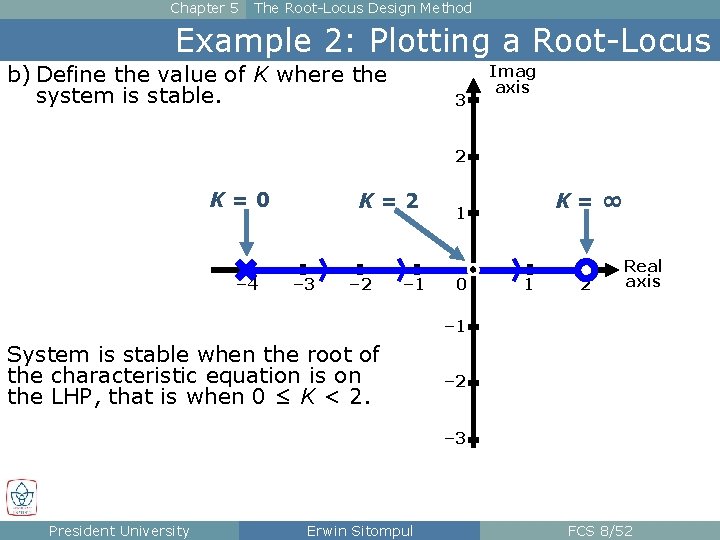
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus b) Define the value of K where the system is stable. 3 Imag axis 2 K=0 – 4 K=2 – 3 – 2 – 1 K=∞ 1 0 1 2 Real axis – 1 System is stable when the root of the characteristic equation is on the LHP, that is when 0 ≤ K < 2. – 2 – 3 President University Erwin Sitompul FCS 8/52

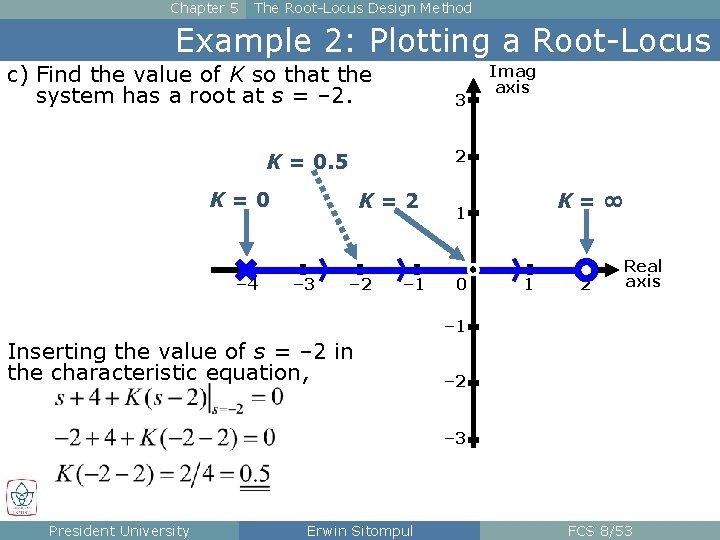
Chapter 5 The Root-Locus Design Method Example 2: Plotting a Root-Locus c) Find the value of K so that the system has a root at s = – 2. 3 2 K = 0. 5 K=0 – 4 K=2 – 3 Imag axis – 2 – 1 K=∞ 1 0 1 2 Real axis – 1 Inserting the value of s = – 2 in the characteristic equation, – 2 – 3 President University Erwin Sitompul FCS 8/53

Chapter 5 The Root-Locus Design Method Example 3: Plotting a Root-Locus For a system with a unity feedback forward-path transfer function a) Determine the break-in/ break-away points. b) Determine the range of steady-state error for a unit ramp input if the system is underdamped. c) Draw the root-locus sketch of the sytem. President University Erwin Sitompul FCS 8/54

Chapter 5 The Root-Locus Design Method Example 4: Plotting a Root-Locus Draw the root-locus plot of the following system. President University Erwin Sitompul FCS 8/55

Chapter 5 The Root-Locus Design Method Homework 8 (1/3) n No. 1, FPE (6 th Ed. ), 5. 2. Hint: Easier way is to assign reasonable values for the zeros and poles in each figure. Later, use MATLAB to draw the Root-Locus. Submit the plot from MATLAB. n No. 2, FPE (6 th Ed. ), 5. 7. (b) Hint: After completing the hand sketch, verify your result using MATLAB. Try to play around with Data Cursor. n No. 3 Sketch the Root-Locus diagram of the following closed-loop system as accurate as possible. n Deadline: One day before the next lecture. President University Erwin Sitompul FCS 8/56

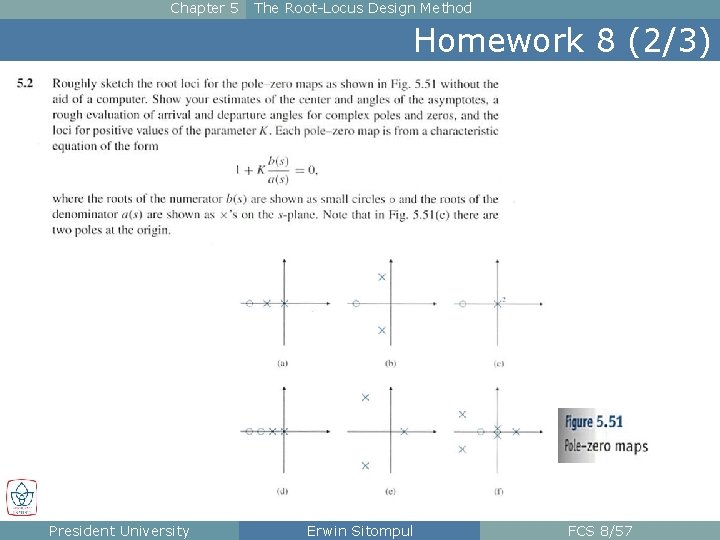
Chapter 5 The Root-Locus Design Method Homework 8 (2/3) President University Erwin Sitompul FCS 8/57

Chapter 5 The Root-Locus Design Method Homework 8 (3/3) President University Erwin Sitompul FCS 8/58