Feedback Control Systems FCS Lecture14 15 State Space

Feedback Control Systems (FCS) Lecture-14 -15 State Space Canonical forms Dr. Imtiaz Hussain email: imtiaz. hussain@faculty. muet. edu. pk URL : http: //imtiazhussainkalwar. weebly. com/

Lecture Outline – Canonical forms of State Space Models • Phase Variable Canonical Form • Controllable Canonical form • Observable Canonical form – Similarity Transformations • Transformation of coordinates – Transformation to CCF – Transformation OCF

Canonical Forms • Canonical forms are the standard forms of state space models. • Each of these canonical form has specific advantages which makes it convenient for use in particular design technique. • There are several canonical forms of state space models – – – Phase variable canonical form Controllable Canonical form Companion forms Observable Canonical form Diagonal Canonical form Modal forms Jordan Canonical Form • It is interesting to note that the dynamics properties of system remain unchanged whichever the type of representation is used.

Phase Variable Canonical form • The method of phase variables possess mathematical advantage over other representations. • This type of representation can be obtained directly from differential equations. • Decomposition of transfer function also yields Phase variable form.

Phase Variable Canonical form • Consider an nth order linear plant model described by the differential equation • Where y(t) is the plant output and u(t) is the plant input. • A state model for this system is not unique but depends on the choice of a set of state variables. • A useful set of state variables, referred to as phase variables, is defined as:

Phase Variable Canonical form • Taking derivatives of the first n-1 state variables, we have

Phase Variable Canonical form • Output equation is simply

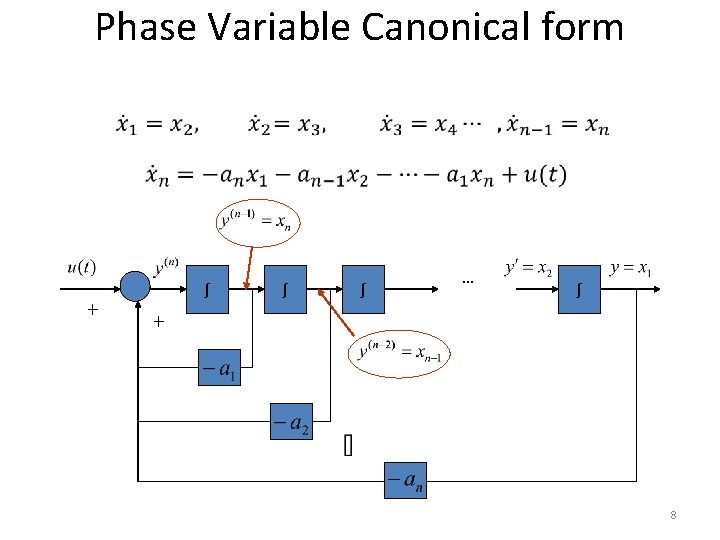
Phase Variable Canonical form ∫ ＋ ∫ ∫ … ∫ ＋ 8

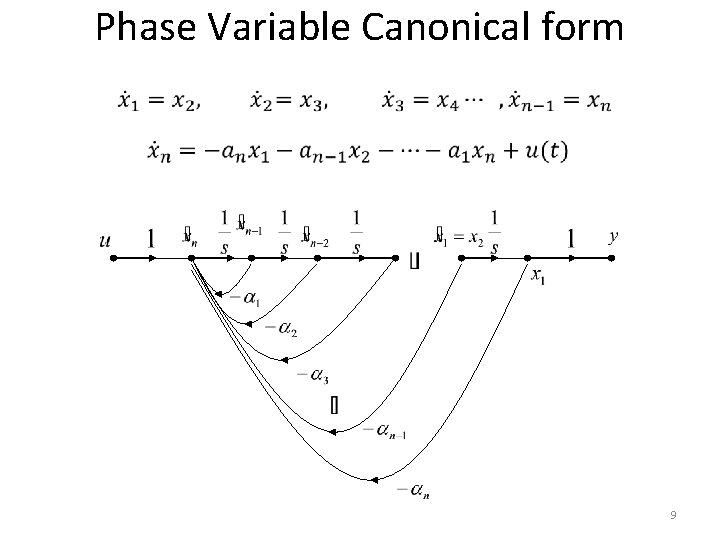
Phase Variable Canonical form 9

Phase Variable Canonical form (Example 1) • Obtain the state equation in phase variable form for the following differential equation, where u(t) is input and y(t) is output. • The differential equation is third order, thus there are three state variables: • And their derivatives are (i. e state equations)

Phase Variable Canonical form (Example 1) • In vector matrix form Home Work: Draw Sate diagram

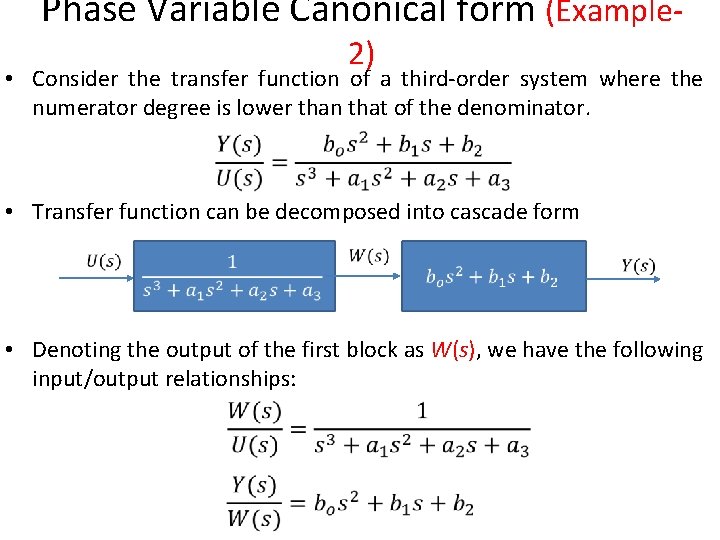
Phase Variable Canonical form (Example 2) • Consider the transfer function of a third-order system where the numerator degree is lower than that of the denominator. • Transfer function can be decomposed into cascade form • Denoting the output of the first block as W(s), we have the following input/output relationships:

Phase Variable Canonical form (Example 2) • Re-arranging above equation yields • Taking inverse Laplace transform of above equations. • Choosing the state variables in phase variable form

Phase Variable Canonical form (Example • State Equations are given as • And the output equation is 1)

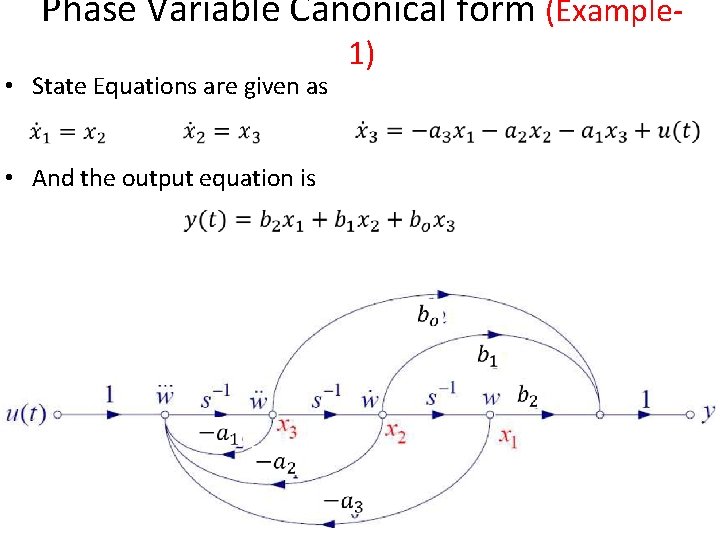
Phase Variable Canonical form (Example • State Equations are given as • And the output equation is 1)

Phase Variable Canonical form (Example • State Equations are given as • And the output equation is • In vector matrix form 1)

Companion Forms • Consider a system defined by • where u is the input and y is the output. • This equation can also be written as • We will present state-space representations of the system defined by above equations in controllable canonical form and observable canonical form.

Controllable Canonical Form • The following state-space representation is called a controllable canonical form:

Controllable Canonical Form

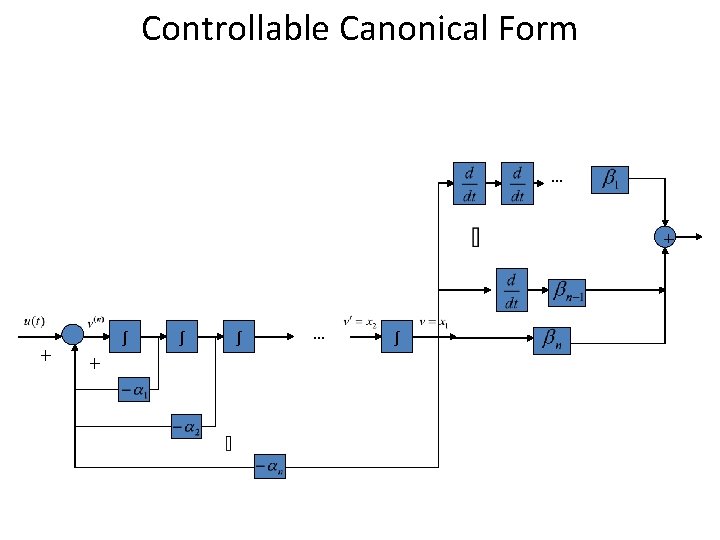
Controllable Canonical Form … ＋ ＋ ∫ ∫ … ∫

Controllable Canonical Form (Example) • Let us Rewrite the given transfer function in following form

Controllable Canonical Form (Example)

Controllable Canonical Form (Example) • By direct decomposition of transfer function • Equating Y(s) with numerator on the right hand side and U(s) with denominator on right hand side.

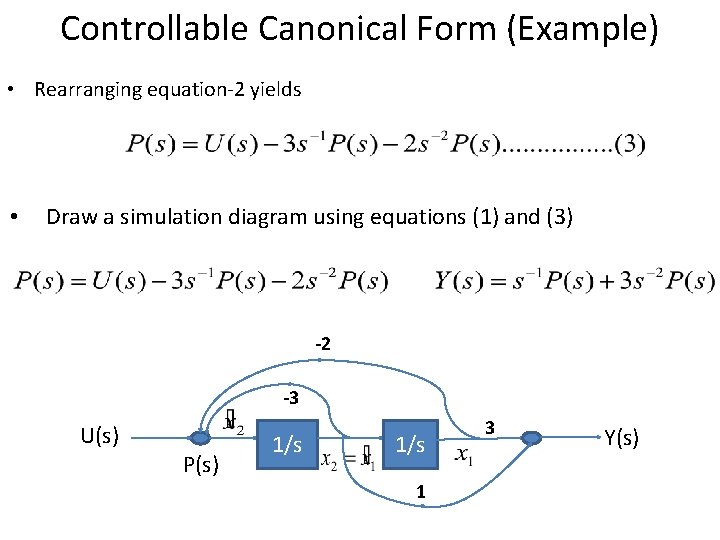
Controllable Canonical Form (Example) • Rearranging equation-2 yields • Draw a simulation diagram using equations (1) and (3) -2 -3 U(s) P(s) 1/s 1 3 Y(s)

Controllable Canonical Form (Example) -2 -3 U(s) P(s) 1/s 3 Y(s) 1 • State equations and output equation are obtained from simulation diagram.

Controllable Canonical Form (Example) • In vector Matrix form

Observable Canonical Form • The following state-space representation is called an observable canonical form:

Observable Canonical Form

Observable Canonical Form (Example) • Let us Rewrite the given transfer function in following form

Observable Canonical Form (Example)

Similarity Transformations •

Similarity Transformations •

Similarity Transformations •

Similarity Transformations •

Similarity Transformations • Following relations are used to preform transformation of coordinates algebraically

Similarity Transformations • Invariance of Eigen Values

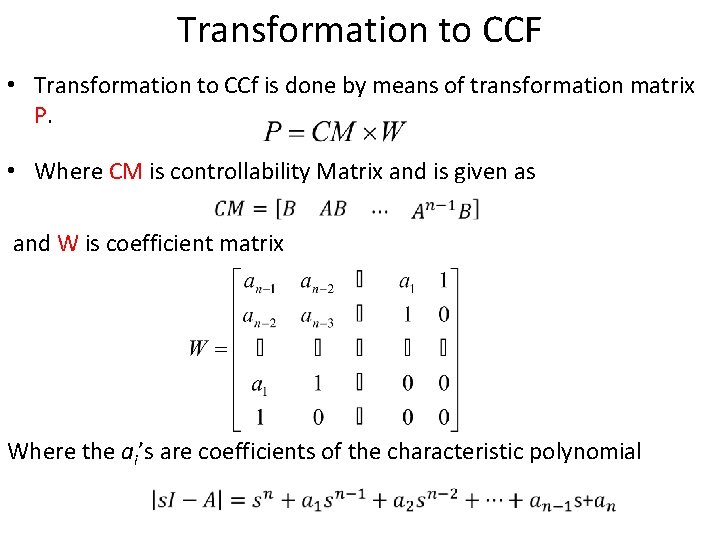
Transformation to CCF • Transformation to CCf is done by means of transformation matrix P. • Where CM is controllability Matrix and is given as and W is coefficient matrix Where the ai’s are coefficients of the characteristic polynomial

Transformation to CCF • Once the transformation matrix P is computed following relations are used to calculate transformed matrices.

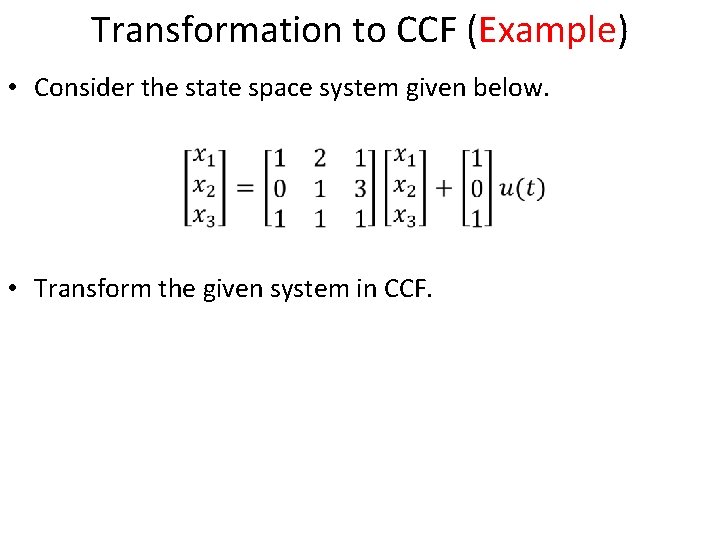
Transformation to CCF (Example) • Consider the state space system given below. • Transform the given system in CCF.

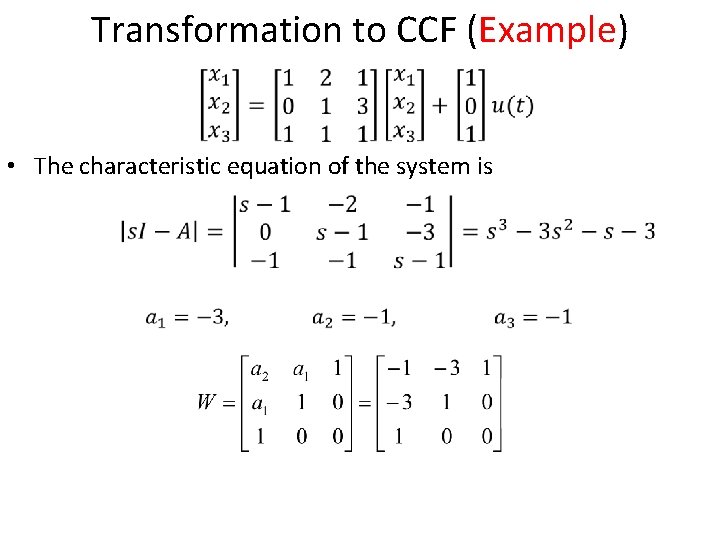
Transformation to CCF (Example) • The characteristic equation of the system is

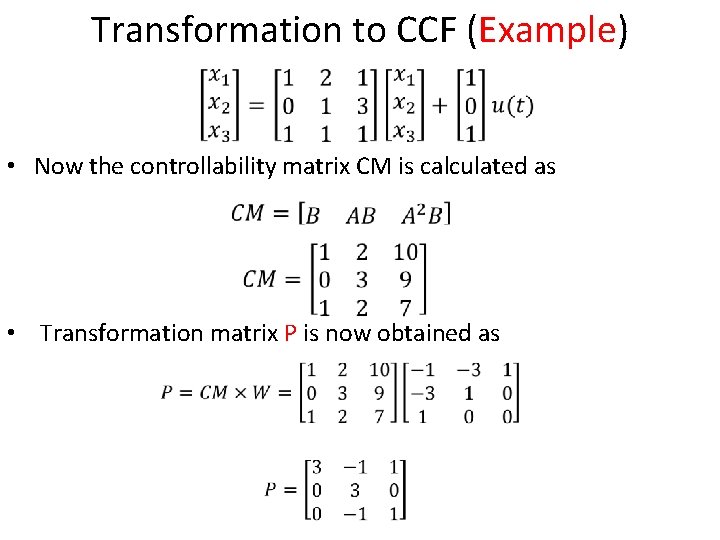
Transformation to CCF (Example) • Now the controllability matrix CM is calculated as • Transformation matrix P is now obtained as

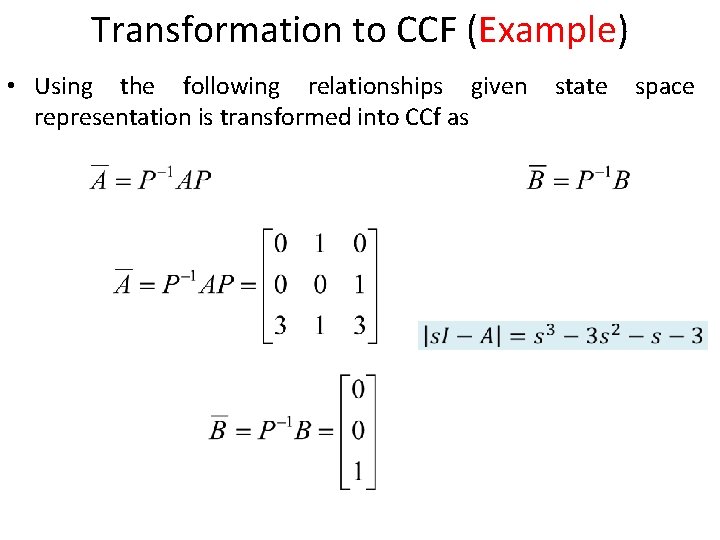
Transformation to CCF (Example) • Using the following relationships given representation is transformed into CCf as state space

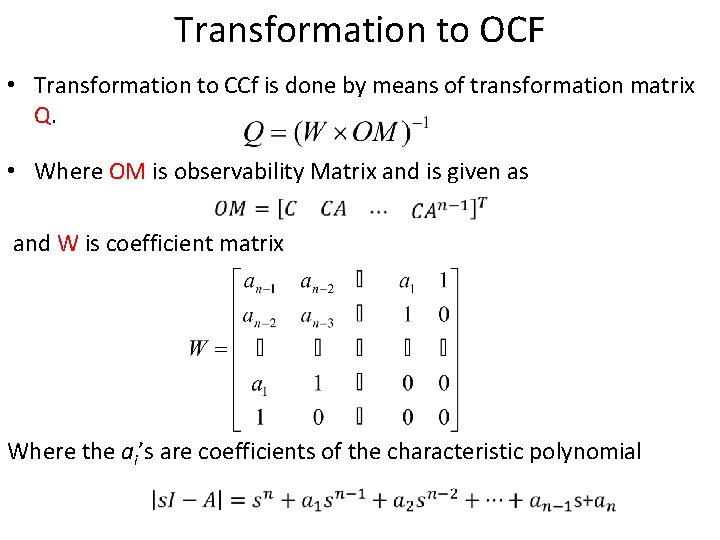
Transformation to OCF • Transformation to CCf is done by means of transformation matrix Q. • Where OM is observability Matrix and is given as and W is coefficient matrix Where the ai’s are coefficients of the characteristic polynomial

Transformation to OCF • Once the transformation matrix Q is computed following relations are used to calculate transformed matrices.

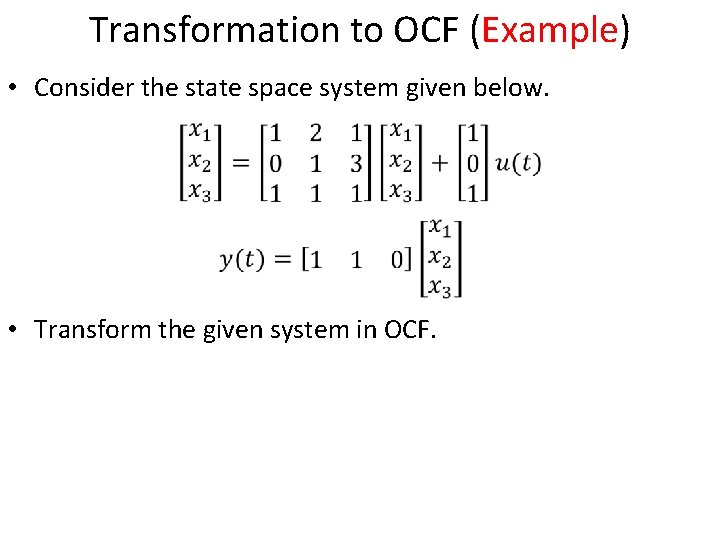
Transformation to OCF (Example) • Consider the state space system given below. • Transform the given system in OCF.

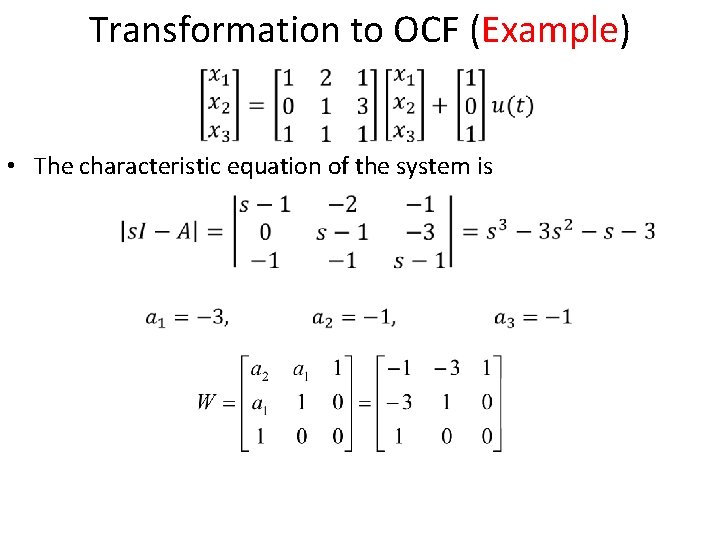
Transformation to OCF (Example) • The characteristic equation of the system is

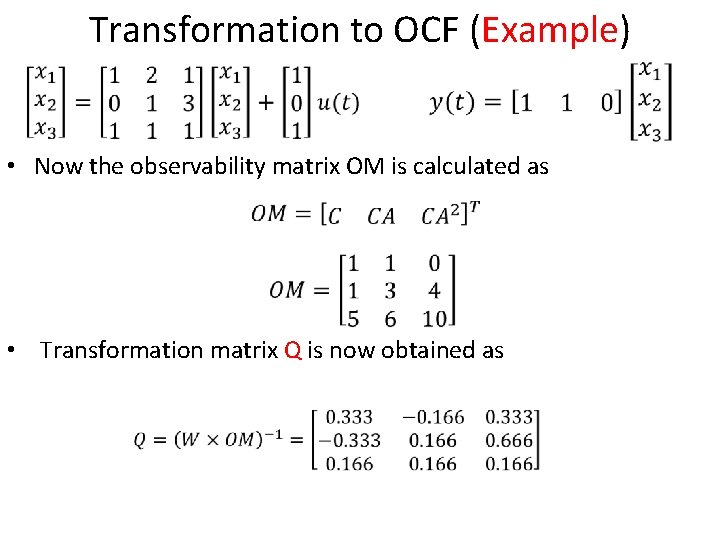
Transformation to OCF (Example) • Now the observability matrix OM is calculated as • Transformation matrix Q is now obtained as

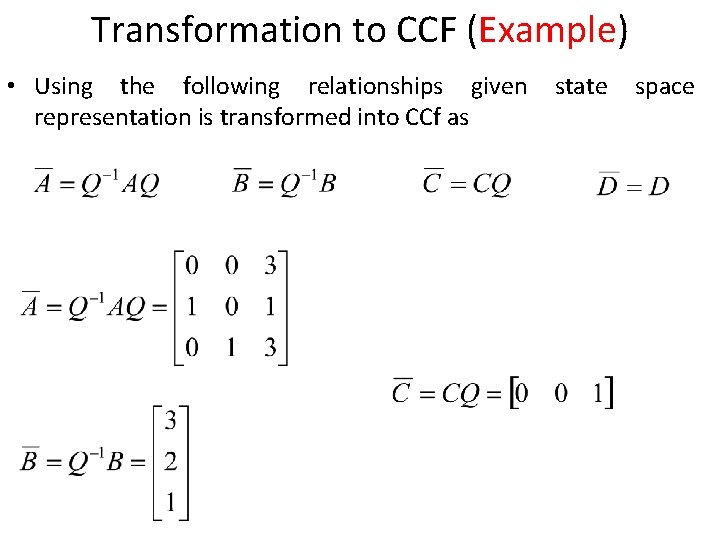
Transformation to CCF (Example) • Using the following relationships given representation is transformed into CCf as state space

Home Work • Obtain state space representation of following transfer function in Phase variable canonical form, OCF and CCF by – Direct Decomposition of Transfer Function – Similarity Transformation – Direct Approach

To download this lecture visit http: //imtiazhussainkalwar. weebly. com/ END OF LECTURES-14 -15