FEEDBACK CONTROL SYSTEMS Dr Basil Hamed Key Words

FEEDBACK CONTROL SYSTEMS Dr. Basil Hamed

Key Words: • • • Feedback Systems Automatic Control Estimation & Identification Mathematical Modeling Process Optimization Decision Making
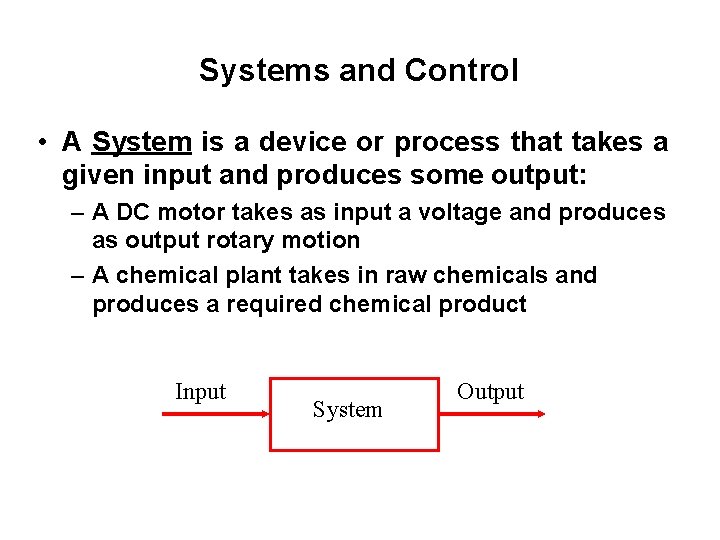
Systems and Control • A System is a device or process that takes a given input and produces some output: – A DC motor takes as input a voltage and produces as output rotary motion – A chemical plant takes in raw chemicals and produces a required chemical product Input System Output
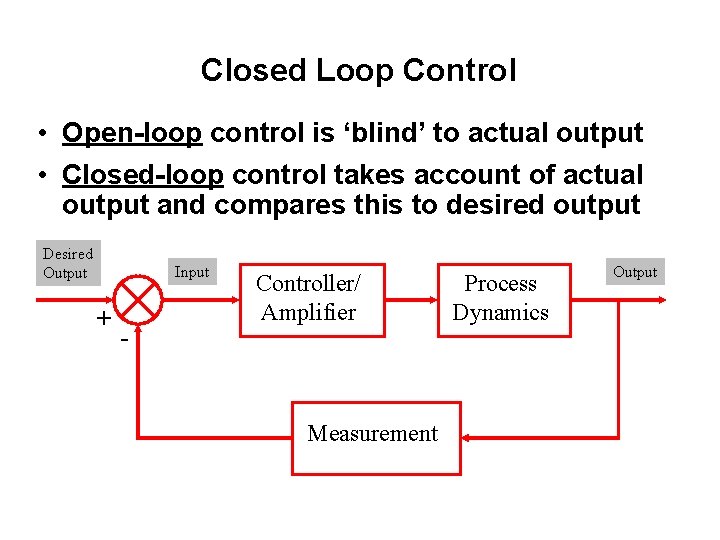
Closed Loop Control • Open-loop control is ‘blind’ to actual output • Closed-loop control takes account of actual output and compares this to desired output Desired Output Input + - Controller/ Amplifier Measurement Process Dynamics Output

An Open-Loop Control System • The controlled ‘output’ is the resulting toast • System does not reject changes in component characteristics
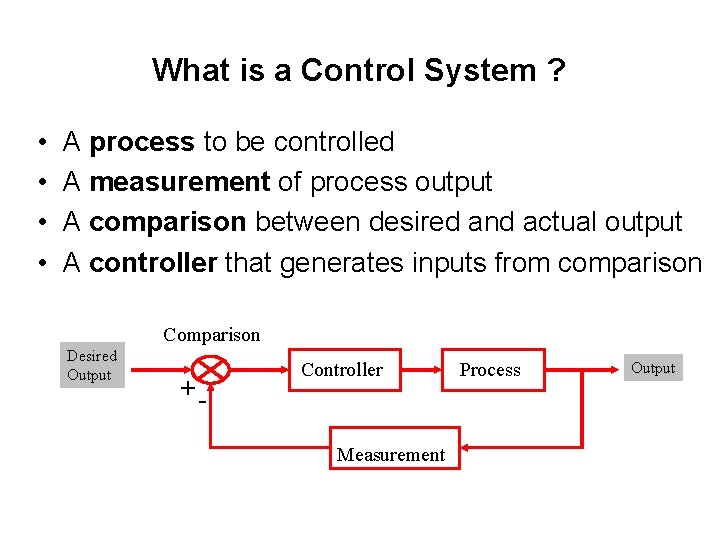
What is a Control System ? • • A process to be controlled A measurement of process output A comparison between desired and actual output A controller that generates inputs from comparison Comparison Desired Output +- Controller Measurement Process Output
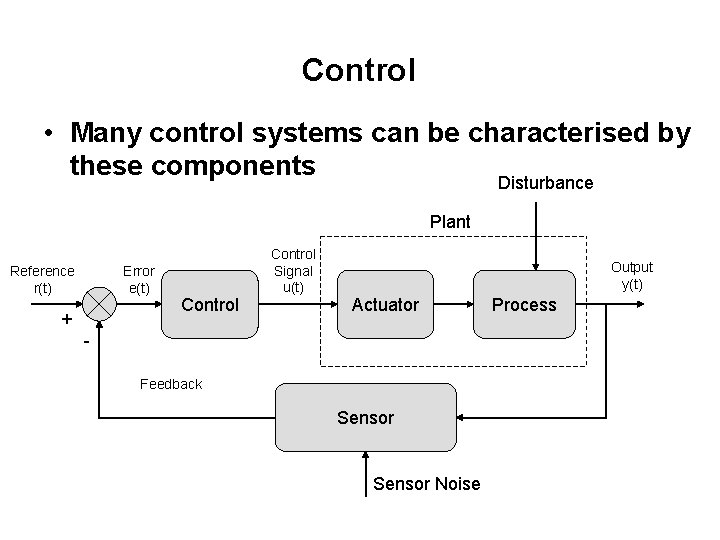
Control • Many control systems can be characterised by these components Disturbance Plant Reference r(t) Error e(t) + Control Signal u(t) Output y(t) Actuator Feedback Sensor Noise Process

Actuation • A device for acting on the environment

Sensing • A device for measuring some aspect of the environment
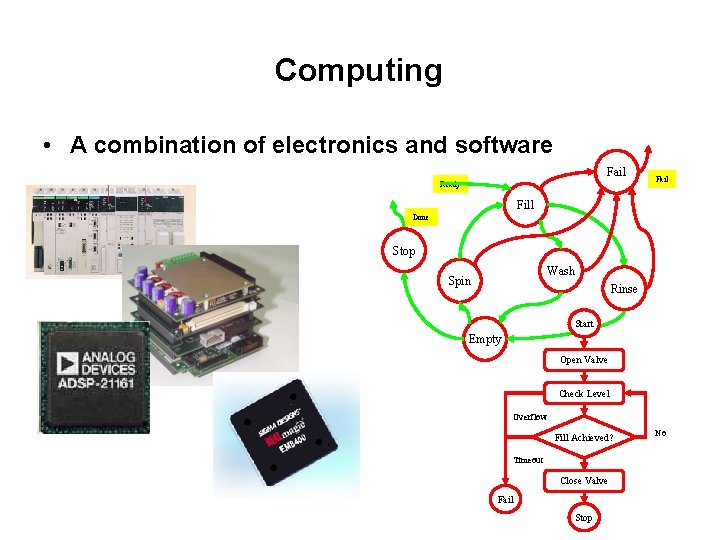
Computing • A combination of electronics and software Fail Ready Fail Fill Done Stop Wash Spin Rinse Start Empty Open Valve Check Level Overflow Fill Achieved? Timeout Yes Close Valve Fail Stop No

Examples of Control Applications Biological Systems: Central Nervous System is the controller for the body Robotics: Robots perform automated tasks in assembly lines, where precision is important and dangerous tasks physically impossible for humans
Examples of Control Applications Aerospace Applications: Aircraft or missile guidance and control Space vehicles and structures

Examples : Washing Machine • System Requirements – Understanding of load sizes – Receptacle to hold clothes – ‘Plumbing’ – Agitation of drum – Ease of use, Reliability – Low Cost • Actuators – AC or DC Motors – Water inlet/drain • Sensors – Water level – Load speed/balance • Control – Choice depends on design

Examples : The CD Player • A CD player is an example of control system • Requires – Accurate positioning of the laser read head – Precise control of media speed – Conversion of digital data to analogue signal

Examples : Hard Drive • A computer disk drive is another example of a rotary control system • Requires – Accurate positioning of the magnetic read head – Precise control of media speed – Extraction of digital data from magnetic media

Examples : Modern Automobiles • Modern Automobiles are controlled by a number of computer components • Requires – Control of automobile sub systems • • • Brakes and acceleration Cruise control ABS Climate control GPS – Reliability – Low cost – Ease of use

Example: DC Motor Speed Control • Desired speed wd • • Actual speed w Tachometer measurements plus noise Control signal is a voltage Variations in Load Torque wd + - Controller Power Amplifier Actual Speed Measurement Tacho Motor w Load Torque
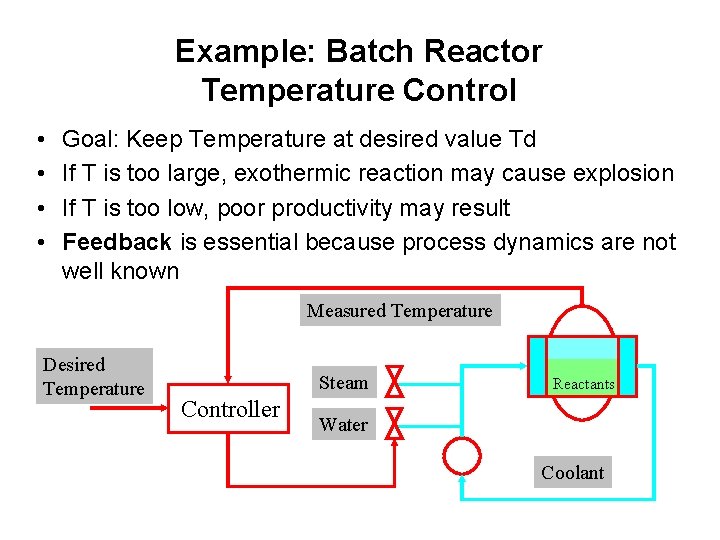
Example: Batch Reactor Temperature Control • • Goal: Keep Temperature at desired value Td If T is too large, exothermic reaction may cause explosion If T is too low, poor productivity may result Feedback is essential because process dynamics are not well known Measured Temperature Desired Temperature Steam Controller Reactants Water Coolant
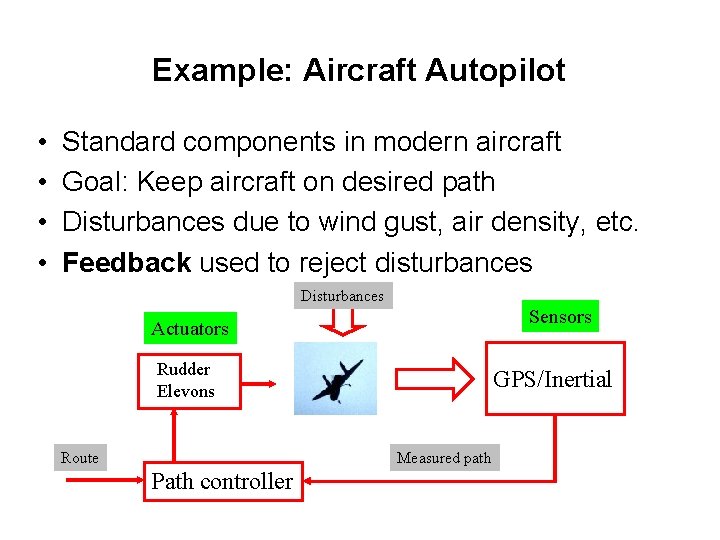
Example: Aircraft Autopilot • • Standard components in modern aircraft Goal: Keep aircraft on desired path Disturbances due to wind gust, air density, etc. Feedback used to reject disturbances Disturbances Sensors Actuators Rudder Elevons Route GPS/Inertial Measured path Path controller
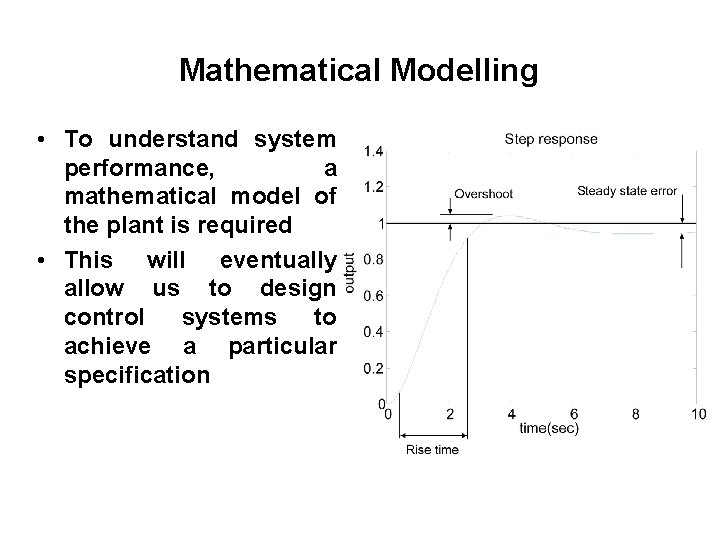
Mathematical Modelling • To understand system performance, a mathematical model of the plant is required • This will eventually allow us to design control systems to achieve a particular specification

Block Diagrams • Formalise control systems as ‘pictures’ • Components can be combined to produce an overall mathematical description of systems • Interaction between elements is well defined

Block Diagrams: Summation • Ideal, no delay or dynamics • Two inputs: • Three or more:
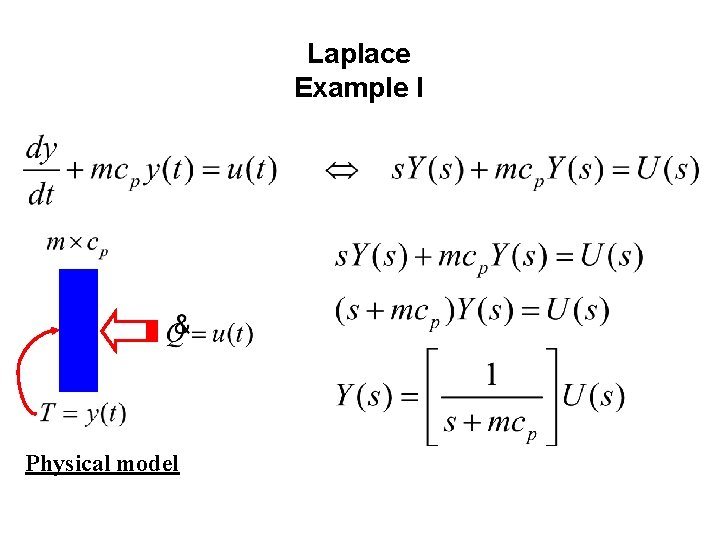
Laplace Example I Physical model
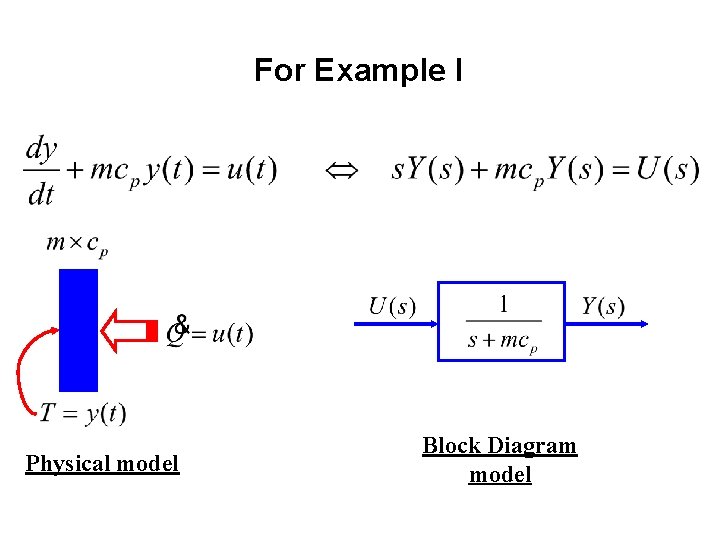
For Example I Physical model Block Diagram model
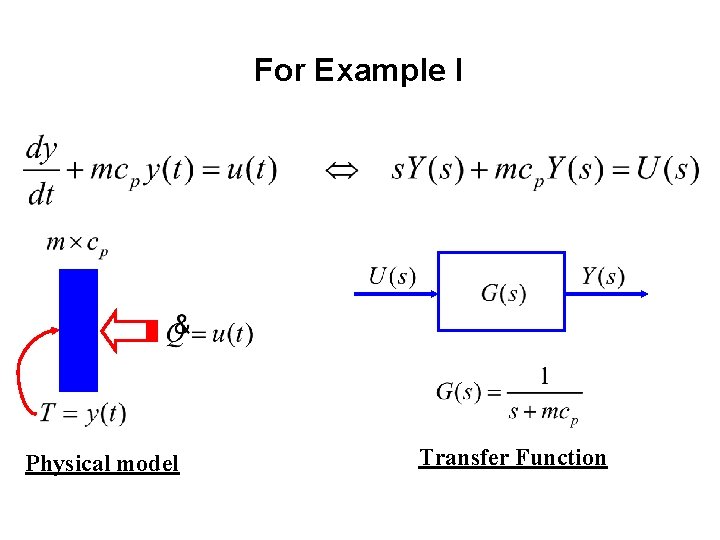
For Example I Physical model Transfer Function
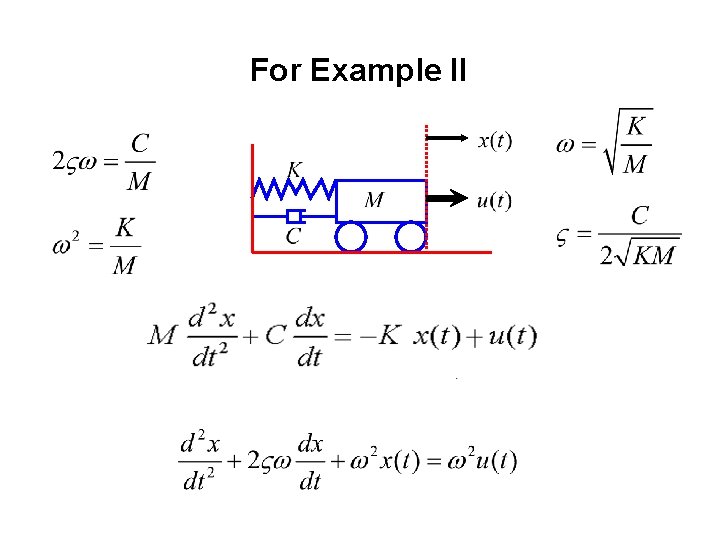
For Example II

For Example II Laplace Transform
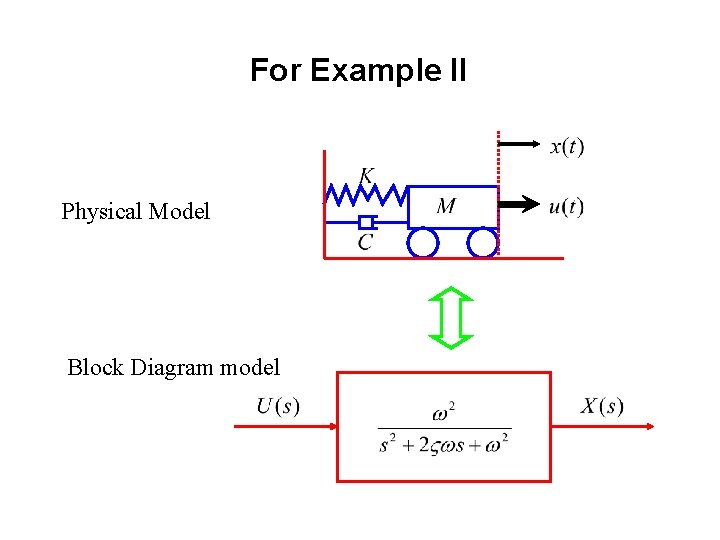
For Example II Physical Model Block Diagram model
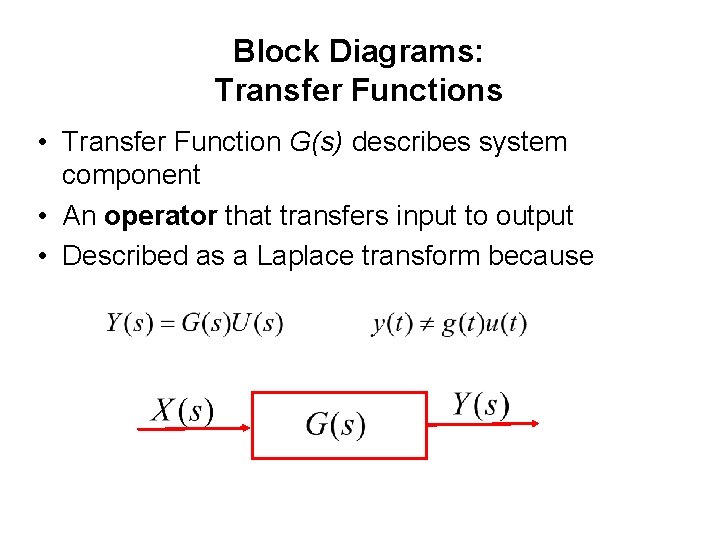
Block Diagrams: Transfer Functions • Transfer Function G(s) describes system component • An operator that transfers input to output • Described as a Laplace transform because
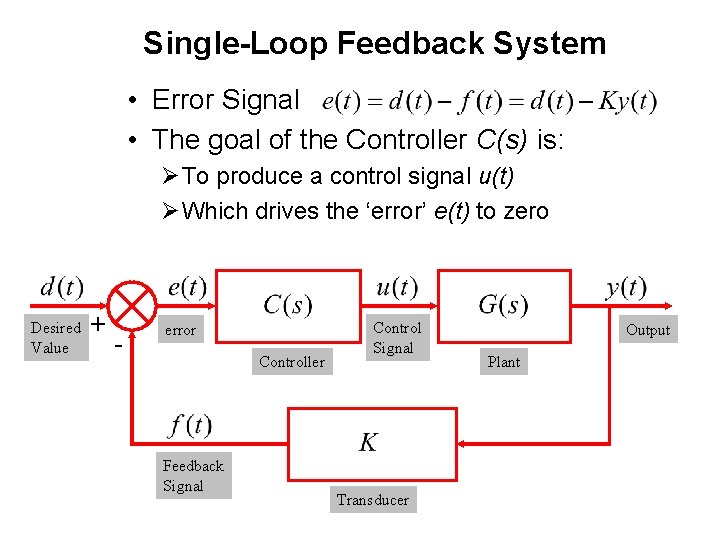
Single-Loop Feedback System • Error Signal • The goal of the Controller C(s) is: Ø To produce a control signal u(t) Ø Which drives the ‘error’ e(t) to zero Desired Value + - error Controller Feedback Signal Control Signal Transducer Output Plant

Controller Objectives • Controller cannot drive error to zero instantaneously as the plant G(s) has dynamics • Clearly a ‘large’ control signal will move the plant more quickly • The gain of the controller should be large so that even small values of e(t) will produce large values of u(t) • However, large values of gain will cause instability

Control Criteria • Speed of Response • Robustness to unknown plant and load • Stability

Response of a First-Order System General Solution:
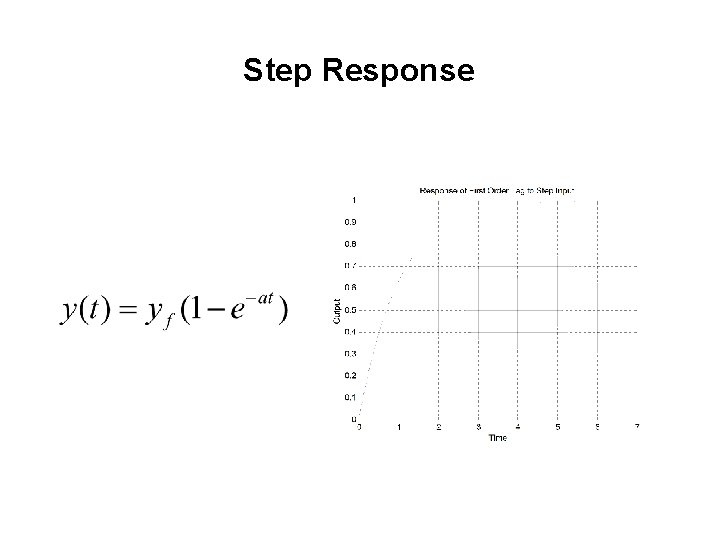
Step Response
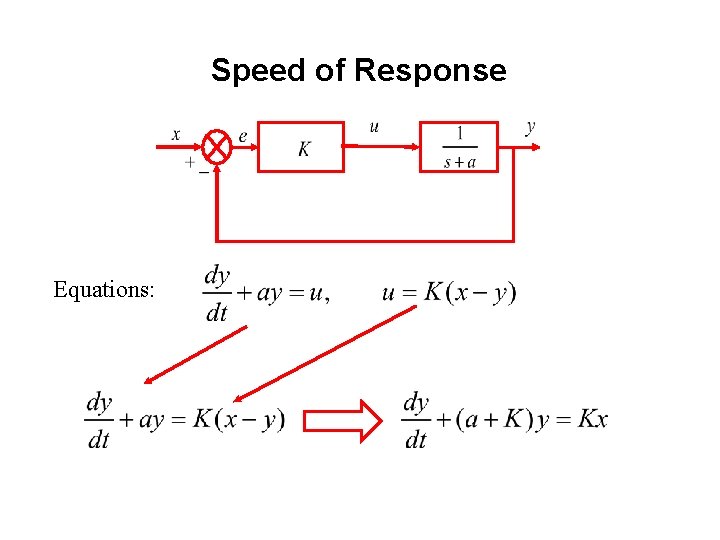
Speed of Response Equations:
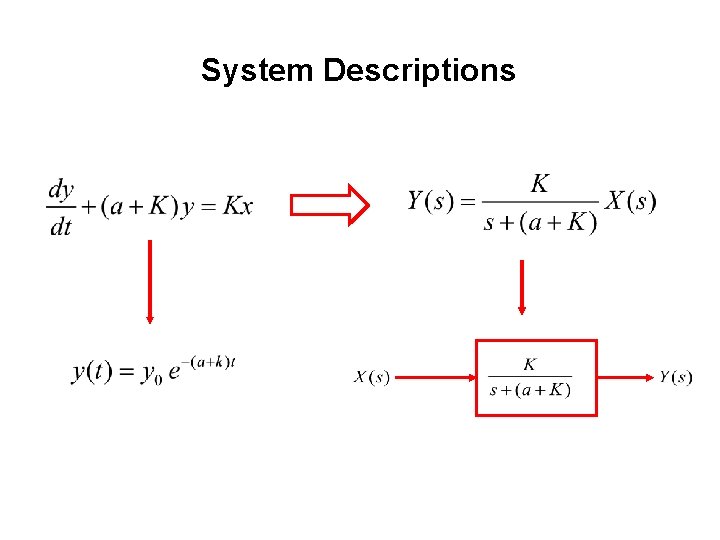
System Descriptions
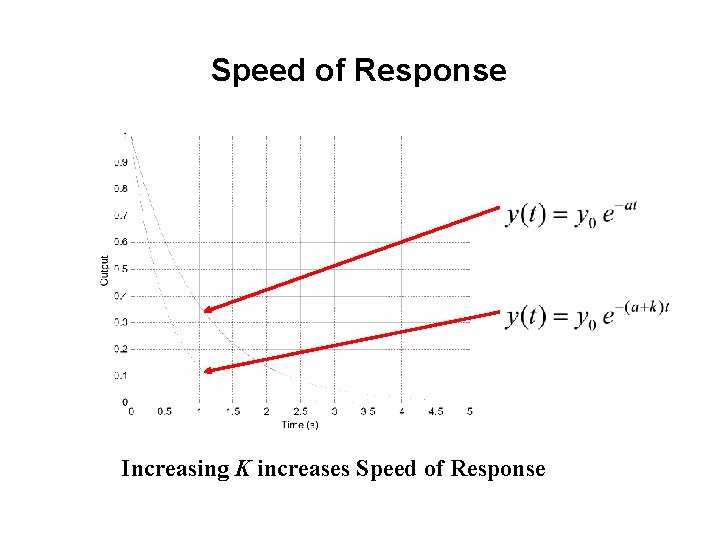
Speed of Response Increasing K increases Speed of Response
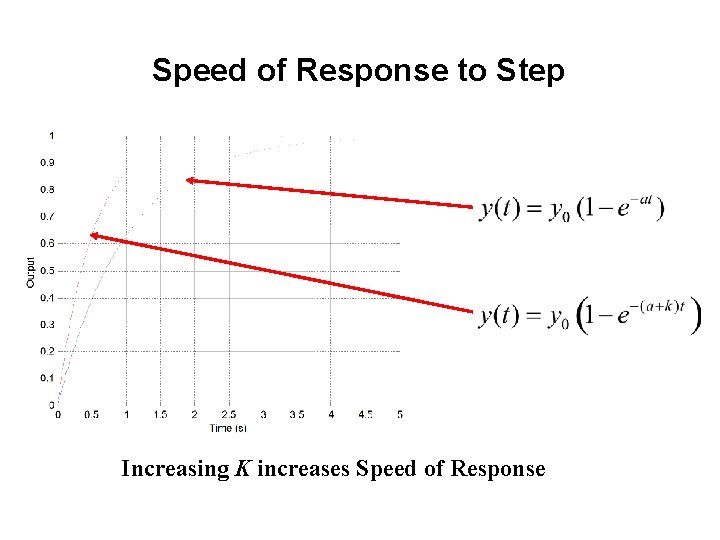
Speed of Response to Step Increasing K increases Speed of Response
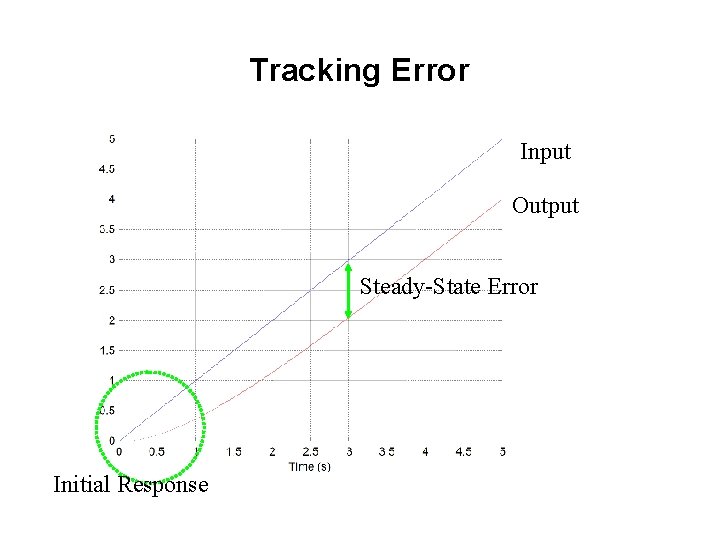
Tracking Error Input Output Steady-State Error Initial Response
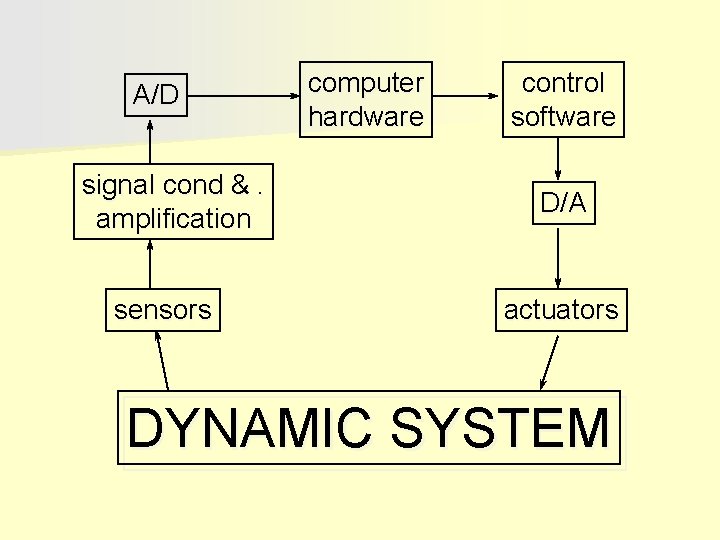
A/D signal cond &. amplification sensors computer hardware control software D/ A actuators DYNAMIC SYSTEM
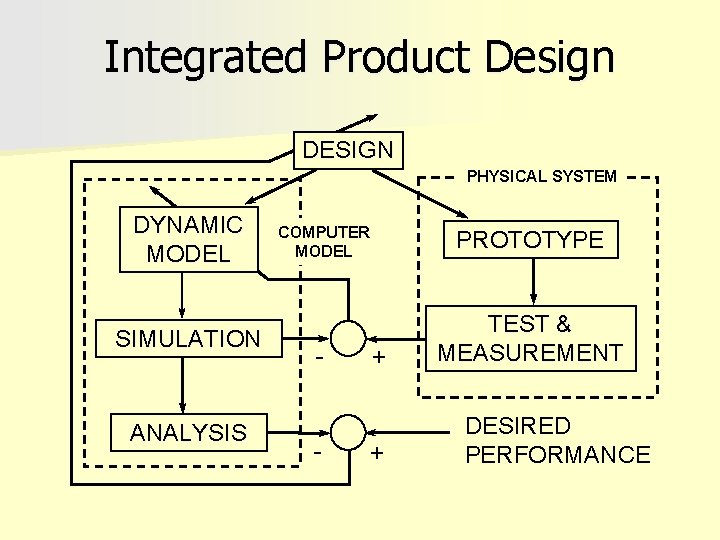
Integrated Product Design DESIGN PHYSICAL SYSTEM DYNAMIC MODEL SIMULATION ANALYSIS COMPUTER MODEL PROTOTYPE - TEST & MEASUREMENT - + + DESIRED PERFORMANCE

A Word About Stability Bigger here Start here BANG ! 180 o phase inversion Another phase inversion If G is such that input is phase reversed (180 o out of phase) for any frequency, then input will be back in phase If System is unstable for one input, it will be unstable for all inputs 42 If loop gain >1 then system will be unstable

Thank you and good luck in your Final Exams
- Slides: 43