Feedback Control System Dr Ing Erwin Sitompul Textbook

Feedback Control System Dr. -Ing. Erwin Sitompul

Textbook and Syllabus Textbook: Gene F. Franklin, J. David Powell, Abbas Emami-Naeini, “Feedback Control of Dynamic Systems”, 6 th Edition, Pearson International Edition. Syllabus: 1. 2. 3. 4. 5. 6. IDR 192, 000 Introduction Dynamic Models Dynamic Response A First Analysis of Feedback The Root-Locus Design Method The Frequency-Response Design Method USD 112. 50 Erwin Sitompul Feedback Control System 1/2

Grade Policy Final Grade = 10% Homework + 20% Quizzes + 30% Midterm Exam + 40% Final Exam + Extra Points § Homeworks will be given in fairly regular basis. The average of homework grades contributes 10% of final grade. § Homeworks are to be written on A 4 papers, otherwise they will not be graded. § Homeworks must be submitted on time. If you submit late, < 10 min. No penalty 10 – 60 min. – 20 points > 60 min. – 40 points § There will be 3 quizzes. Only the best 2 will be counted. The average of quiz grades contributes 20% of final grade. Erwin Sitompul Feedback Control System 1/3

Grade Policy § Midterm and final exam schedule will be announced in time. § Make up of quizzes and exams will be held one week after the schedule of the respective quizzes and exams, at the latest. § The score of a make up quiz or exam can be multiplied by 0. 9 (the maximum score for a make up is 90). § Extra points will be given every time you solve a problem in front of the class. You will earn 1 or 2 points. Erwin Sitompul Feedback Control System 1/4

Chapter 1 INTRODUCTION Feedback Control System Dr. -Ing. Erwin Sitompul

Introduction • Control is a series of actions directed for making a system variable adheres to a reference value (can be either constant or variable). • The reference value when performing control is the desired output variable. • Process, as it is used and understood by control engineers, means the component to be controlled. Fundamental structures of control are classified based on the information used along the control process: 1. Open-loop control / Feedforward control 2. Closed-loop control / Feedback control Erwin Sitompul Feedback Control System 1/6

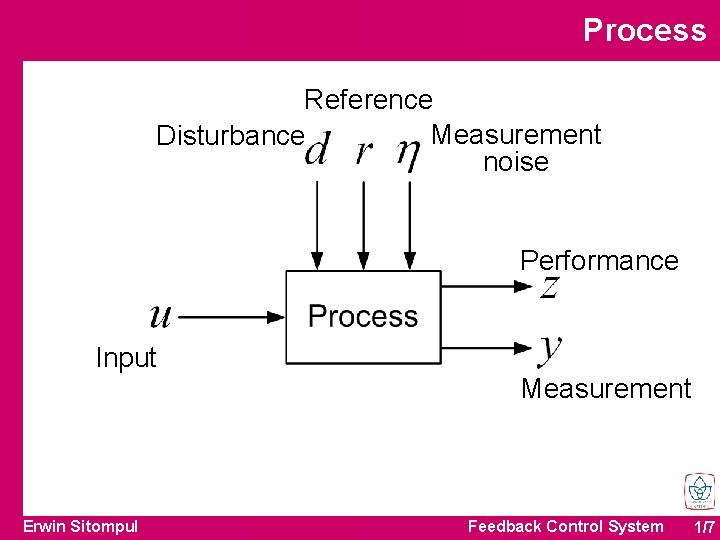
Process Reference Measurement Disturbance noise Performance Input Erwin Sitompul Measurement Feedback Control System 1/7

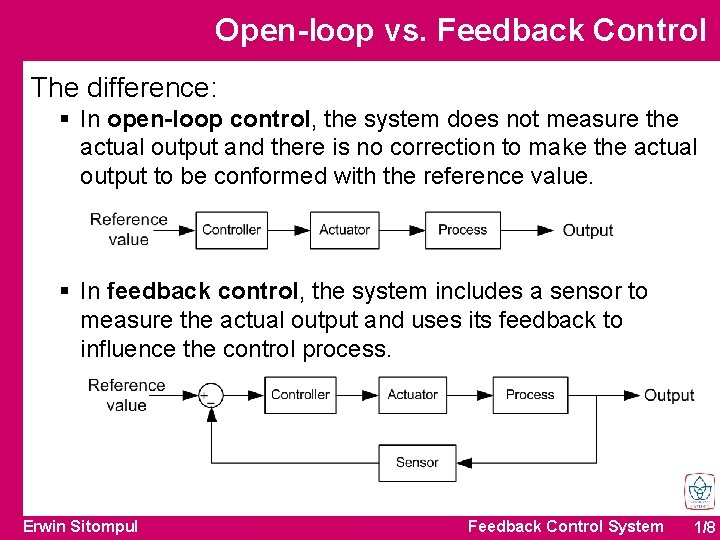
Open-loop vs. Feedback Control The difference: § In open-loop control, the system does not measure the actual output and there is no correction to make the actual output to be conformed with the reference value. § In feedback control, the system includes a sensor to measure the actual output and uses its feedback to influence the control process. Erwin Sitompul Feedback Control System 1/8

Examples Open-loop control Feedback control Example: an electric toaster, a standard gas stove. Example: automated filling up system, magic jar, etc. • The controller is constructed based on knowledge or experience. • The process output is not used in control computation. • The output is fed back for control computation. Erwin Sitompul Feedback Control System 1/9

Plus-Minus of Open-loop Control + Generally simpler than closed-loop control + Does not require sensor to measure the output + Does not, of itself, introduce stability problem – Has lower performance to match the desired output compared to closed-loop control Erwin Sitompul Feedback Control System 1/10

Plus-Minus of Feedback Control – – More complex than open-loop control May have steady-state error Depends on the accuracy of the sensor May have stability problem + Process controlled by well designed feedback control can respond to unforeseen events, such as: disturbance, change of process due to aging, wear, etc. + Eliminates the need of human to adjust the control variable reduce human workload + Gives much better performance than what is possibly given by open loop control: ability to meet transient response objectives and steady-state error objectives Erwin Sitompul Feedback Control System 1/11

Chapter 2 DYNAMIC MODELS Feedback Control System Dr. -Ing. Erwin Sitompul

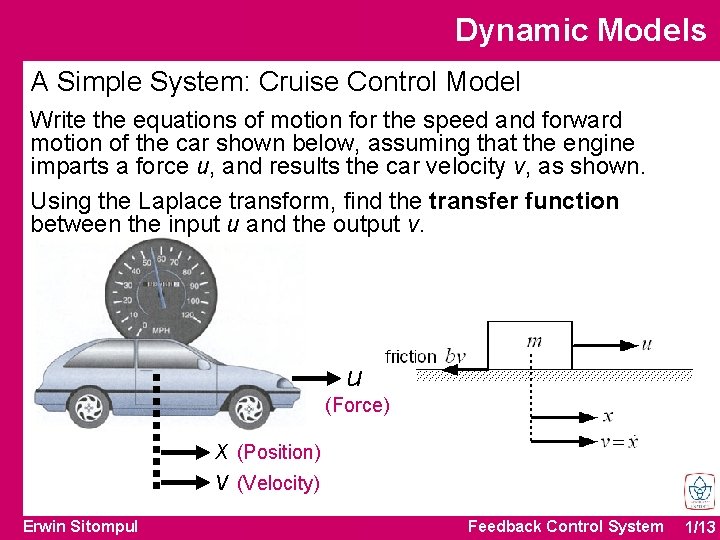
Dynamic Models A Simple System: Cruise Control Model Write the equations of motion for the speed and forward motion of the car shown below, assuming that the engine imparts a force u, and results the car velocity v, as shown. Using the Laplace transform, find the transfer function between the input u and the output v. u (Force) x (Position) v (Velocity) Erwin Sitompul Feedback Control System 1/13

Dynamic Models Applying the Newton’s Law for translational motion yields: MATLAB (Matrix Laboratory) is the standard software used in control engineering: In the end of this course, you are expected to be able to know how to use MATLAB for basic applications. Erwin Sitompul Feedback Control System 1/14

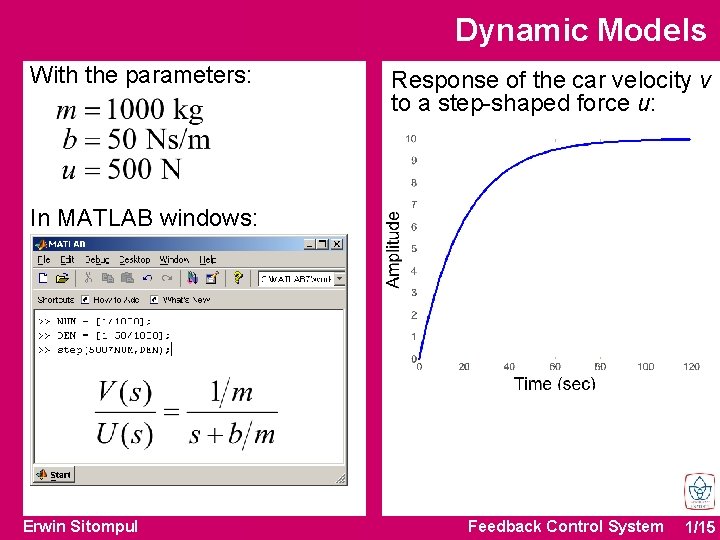
Dynamic Models With the parameters: Response of the car velocity v to a step-shaped force u: In MATLAB windows: Erwin Sitompul Feedback Control System 1/15

Dynamic Models A Two-Mass System: Suspension Model m 1 : mass of the wheel m 2 : mass of the car x, y : displacements from equilibrium r : distance to road surface Equation for m 1: Equation for m 2: Rearranging: Erwin Sitompul Feedback Control System 1/16

Dynamic Models Using the Laplace transform: to transfer from time domain to frequency domain yields: Erwin Sitompul Feedback Control System 1/17

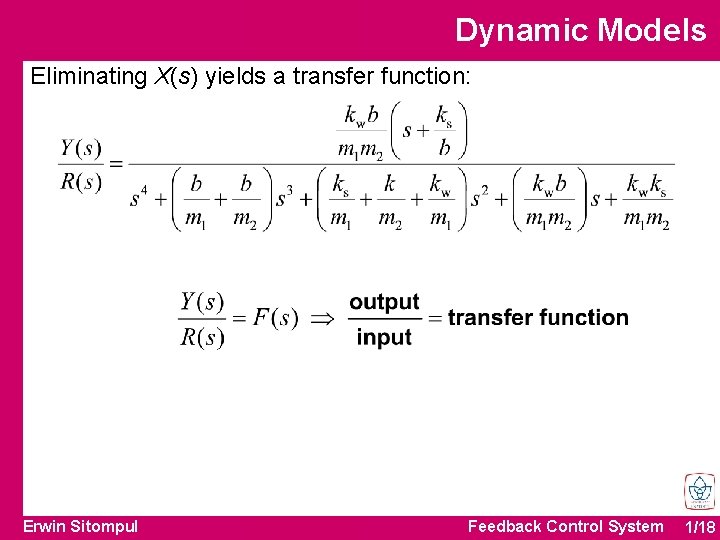
Dynamic Models Eliminating X(s) yields a transfer function: Erwin Sitompul Feedback Control System 1/18

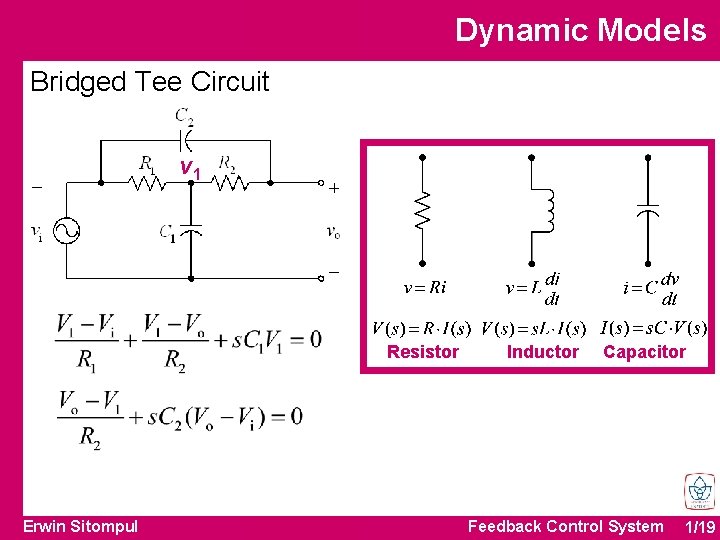
Dynamic Models Bridged Tee Circuit v 1 Resistor Erwin Sitompul Inductor Capacitor Feedback Control System 1/19

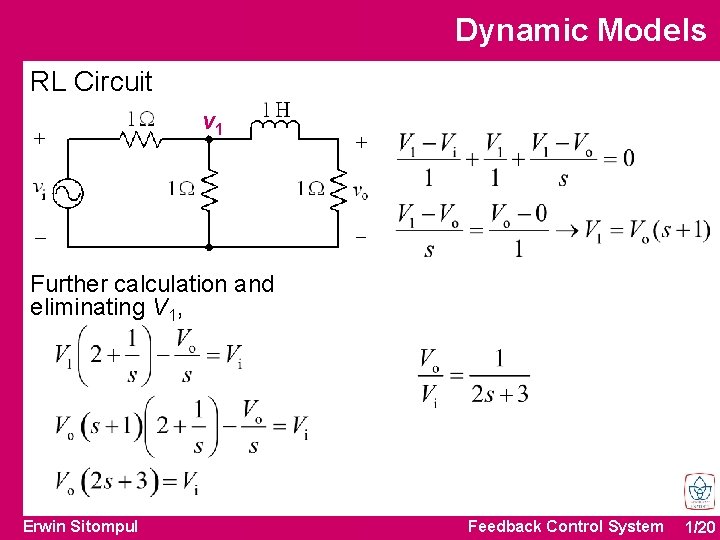
Dynamic Models RL Circuit v 1 Further calculation and eliminating V 1, Erwin Sitompul Feedback Control System 1/20

Chapter 3 DYNAMIC RESPONSE Feedback Control System Dr. -Ing. Erwin Sitompul

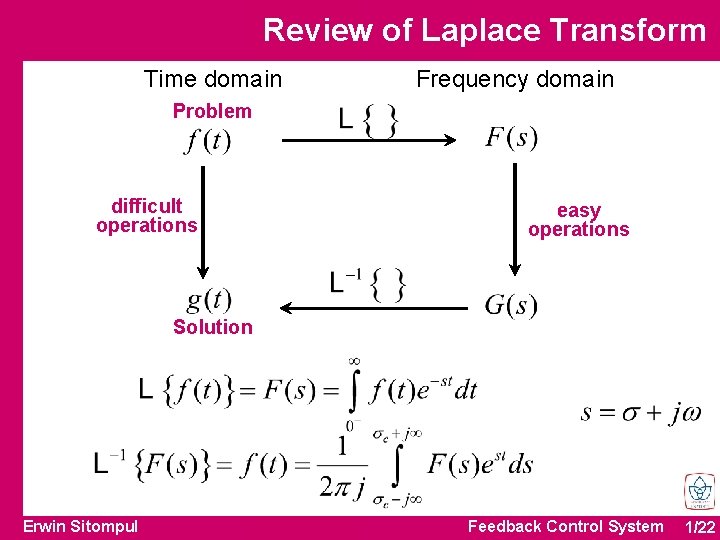
Review of Laplace Transform Time domain Frequency domain Problem difficult operations easy operations Solution Erwin Sitompul Feedback Control System 1/22

Properties of Laplace Transform 1. Superposition 2. Time delay 3. Time scaling 4. Shift in Frequency 5. Differentiation in Time Erwin Sitompul Feedback Control System 1/23

Properties of Laplace Transform 6. Integration in Time 7. Differentiation in Frequency 8. Convolution Erwin Sitompul Feedback Control System 1/24

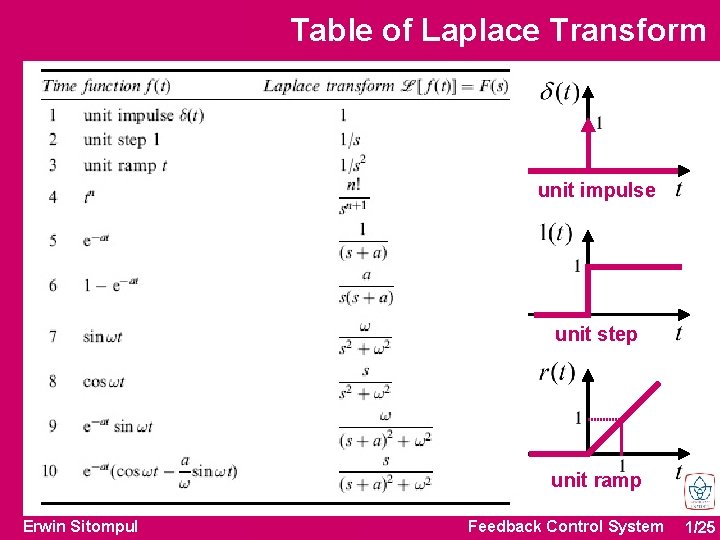
Table of Laplace Transform unit impulse unit step unit ramp Erwin Sitompul Feedback Control System 1/25

Laplace Transform Example: Obtain the Laplace transform of Erwin Sitompul Feedback Control System 1/26

Laplace Transform Example: Find the Laplace transform of the function shown below. Erwin Sitompul Feedback Control System 1/27

Inverse Laplace Transform The steps are: 1. Decompose F(s) into simple terms using partial-fraction expansion. 2. Find the inverse of each term by using the table of Laplace transform. Example: Find y(t) for Erwin Sitompul Feedback Control System 1/28

Inverse Laplace Transform Comparing the coefficients Erwin Sitompul Feedback Control System 1/29

Initial and Final Value Theorem Only applicable to stable system, i. e. a system with convergent step response Example: Find the final value of the system corresponding to Erwin Sitompul Feedback Control System 1/30

Initial and Final Value Theorem Example: Find the final value of the system corresponding to WRONG Since NOT convergent NO limit value Erwin Sitompul Feedback Control System 1/31

Initial and Final Value Theorem Example: Find the final value of WRONG Since periodic signal NOT convergent NO limit value Erwin Sitompul Feedback Control System 1/32

Homework 1 § 2. 6 § 3. 4 (b) § 3. 5 (c) § 3. 6 (e) § Deadline: 10. 05. 2011, 7: 30 am. Erwin Sitompul Feedback Control System 1/33