February 2022 Linear inequality regions LO To identify

February 2022 Linear inequality regions LO: To identify regions defined by inequalities. www. mathssupport. org

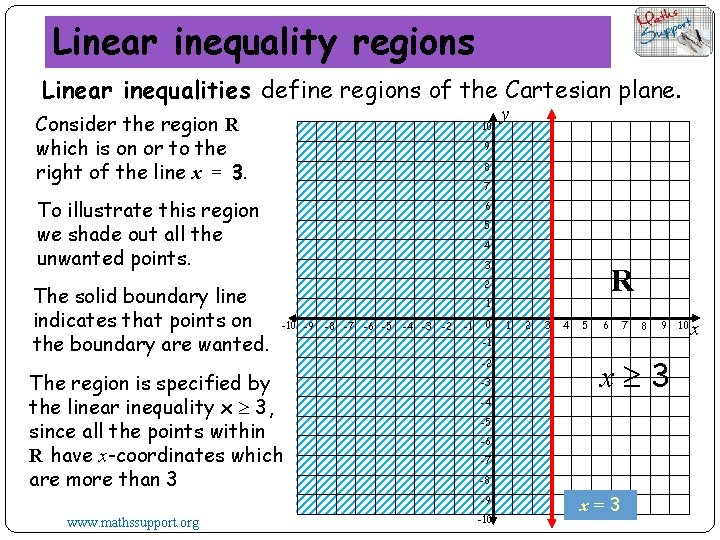
Linear inequality regions Linear inequalities define regions of the Cartesian plane. Consider the region R which is on or to the right of the line x = 3. 10 9 8 7 To illustrate this region we shade out all the unwanted points. The solid boundary line indicates that points on the boundary are wanted. 6 5 4 3 R 2 1 -10 -9 The region is specified by the linear inequality x 3, since all the points within R have x-coordinates which are more than 3 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 -1 -2 -3 -4 x 3 -5 -6 -7 -8 -9 www. mathssupport. org y -10 x=3 10 x

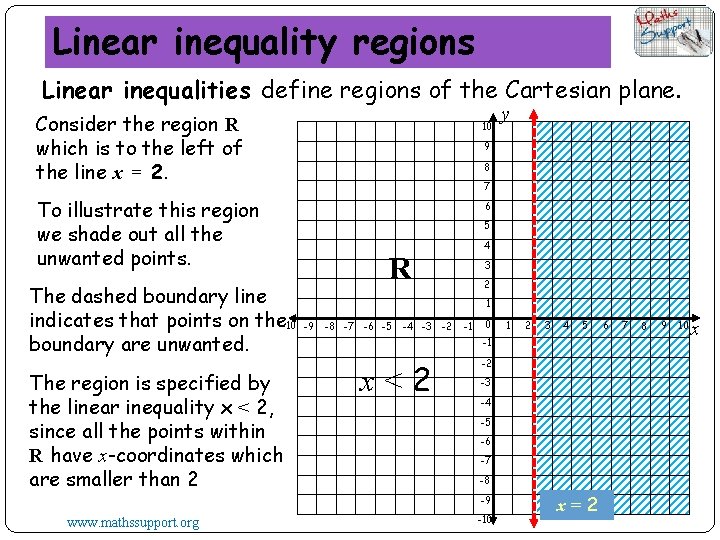
Linear inequality regions Linear inequalities define regions of the Cartesian plane. Consider the region R which is to the left of the line x = 2. 10 9 8 7 To illustrate this region we shade out all the unwanted points. The dashed boundary line indicates that points on the-10 boundary are unwanted. The region is specified by the linear inequality x < 2, since all the points within R have x-coordinates which are smaller than 2 6 5 4 R 3 2 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 -1 x<2 -2 -3 -4 -5 -6 -7 -8 -9 www. mathssupport. org y -10 x=2 6 7 8 9 10 x

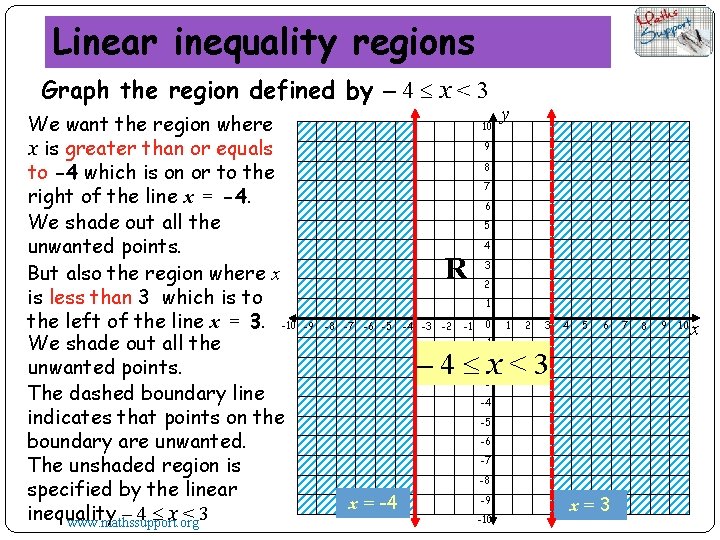
Linear inequality regions Graph the region defined by – 4 x < 3 We want the region where x is greater than or equals to -4 which is on or to the right of the line x = -4. We shade out all the unwanted points. But also the region where x is less than 3 which is to the left of the line x = 3. -10 We shade out all the unwanted points. The dashed boundary line indicates that points on the boundary are unwanted. The unshaded region is specified by the linear inequality – 4 x<3 www. mathssupport. org 10 y 9 8 7 6 5 R 4 3 2 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -1 – 4 x<3 -2 -3 -4 -5 -6 -7 -8 x = -4 -9 -10 x=3 7 8 9 10 x

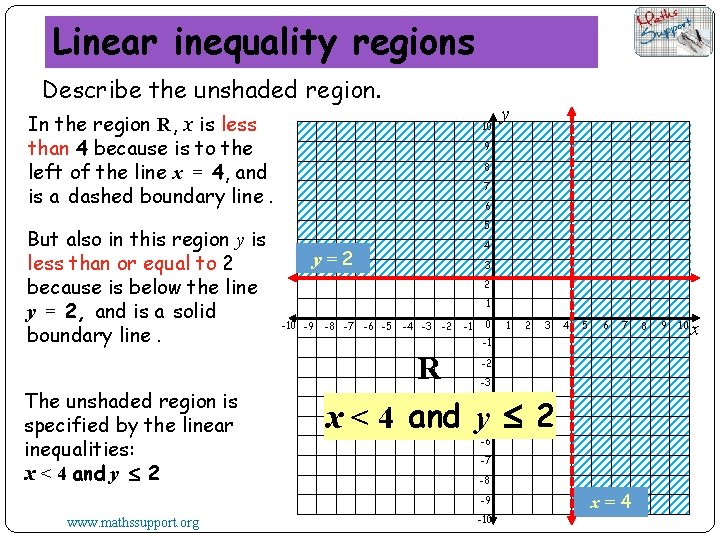
Linear inequality regions Describe the unshaded region. In the region R, x is less than 4 because is to the left of the line x = 4, and is a dashed boundary line. But also in this region y is less than or equal to 2 because is below the line y = 2, and is a solid boundary line. 10 y 9 8 7 6 5 4 y=2 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 -1 R x < 4 and y 2 -2 The unshaded region is specified by the linear inequalities: x < 4 and y 2 -3 -4 -5 -6 -7 -8 -9 www. mathssupport. org -10 x=4 8 9 10 x

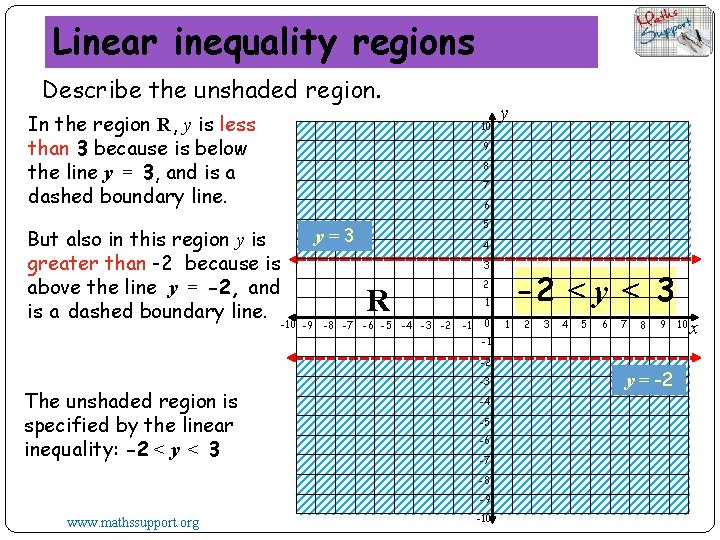
Linear inequality regions Describe the unshaded region. In the region R, y is less than 3 because is below the line y = 3, and is a dashed boundary line. 10 y 9 8 7 6 But also in this region y is greater than -2 because is above the line y = -2, and is a dashed boundary line. -10 -9 5 y=3 4 3 R -8 -7 -6 -5 -2 < y < 3 2 1 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 -1 -2 The unshaded region is specified by the linear inequality: -2 < y < 3 -3 -4 -5 -6 -7 -8 -9 www. mathssupport. org -10 y = -2 10 x

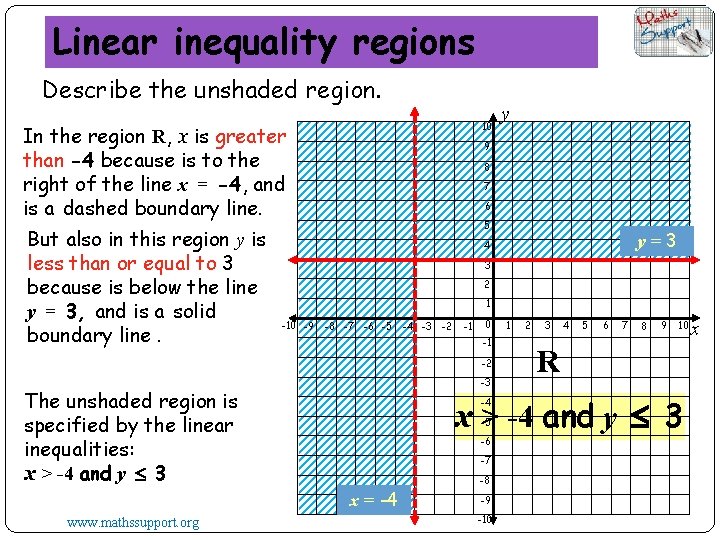
Linear inequality regions Describe the unshaded region. 10 In the region R, x is greater than -4 because is to the right of the line x = -4, and is a dashed boundary line. But also in this region y is less than or equal to 3 because is below the line y = 3, and is a solid boundary line. 9 8 7 6 5 y=3 4 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 The unshaded region is specified by the linear inequalities: x > -4 and y 3 1 2 3 4 5 6 7 8 9 10 R x > -4 and y 3 -4 -5 -6 -7 x = -4 www. mathssupport. org y -8 -9 -10 x

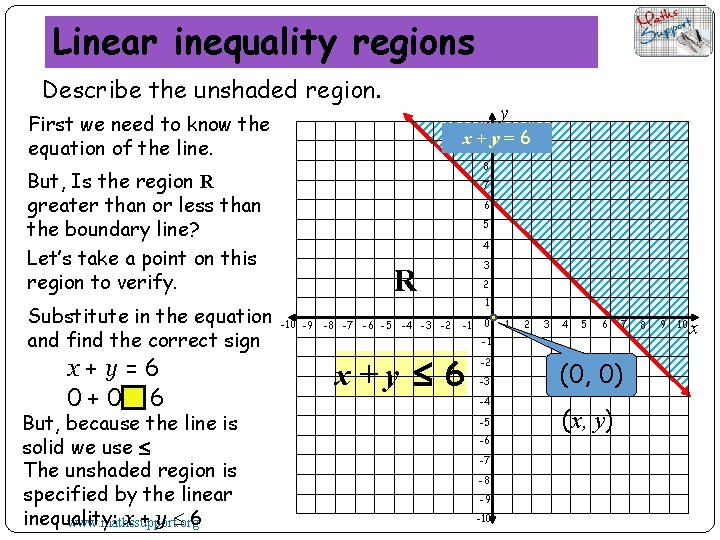
Linear inequality regions Describe the unshaded region. First we need to know the equation of the line. 10 x +9 y = 6 8 But, Is the region R greater than or less than the boundary line? Let’s take a point on this region to verify. Substitute in the equation and find the correct sign x+y=6 0+0<6 But, because the line is solid we use The unshaded region is specified by the linear inequality: x+y 6 www. mathssupport. org y 7 6 5 4 3 R -10 -9 -8 -7 -6 -5 -4 -3 -2 2 1 -1 0 1 2 3 4 5 6 7 -1 x+y 6 -2 -3 -4 -5 -6 -7 -8 -9 -10 (0, 0) (x, y) 8 9 10 x

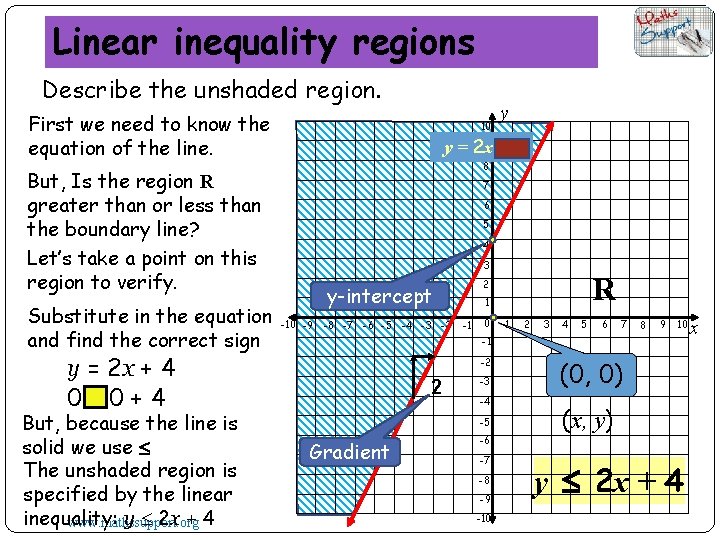
Linear inequality regions Describe the unshaded region. First we need to know the equation of the line. 10 9 + 4 y = 2 x 8 But, Is the region R greater than or less than the boundary line? Let’s take a point on this region to verify. Substitute in the equation and find the correct sign 7 6 5 4 3 -10 -9 -8 -7 -6 -5 -4 -3 -2 R 2 y-intercept 1 -1 0 1 2 3 4 5 6 7 8 9 10 -1 y = 2 x + 4 0<0+4 But, because the line is solid we use The unshaded region is specified by the linear inequality: y 2 x + 4 www. mathssupport. org y -2 2 -3 -4 -5 Gradient -6 -7 -8 -9 -10 (0, 0) (x, y) y 2 x + 4 x

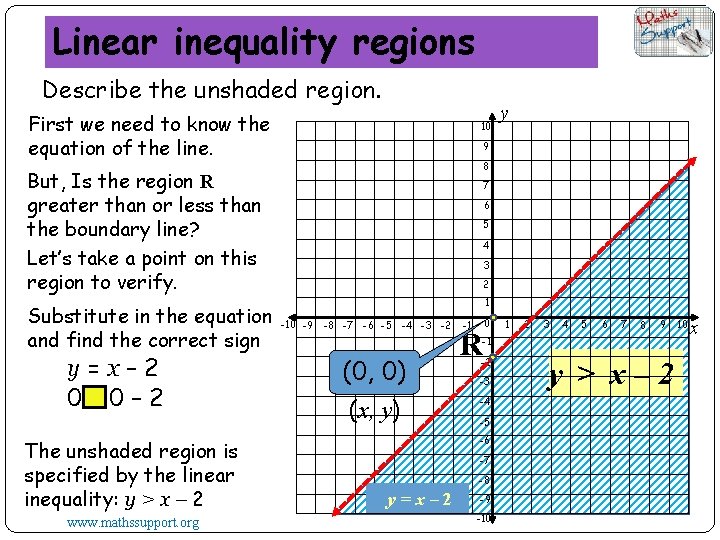
Linear inequality regions Describe the unshaded region. First we need to know the equation of the line. 10 9 8 But, Is the region R greater than or less than the boundary line? Let’s take a point on this region to verify. Substitute in the equation and find the correct sign y=x– 2 0>0– 2 The unshaded region is specified by the linear inequality: y > x – 2 www. mathssupport. org y 7 6 5 4 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 (0, 0) (x, y) -1 R 0 2 3 4 5 6 7 8 9 -1 -2 -3 -4 -5 -6 -7 -8 y=x– 2 1 -9 -10 y > x– 2 10 x

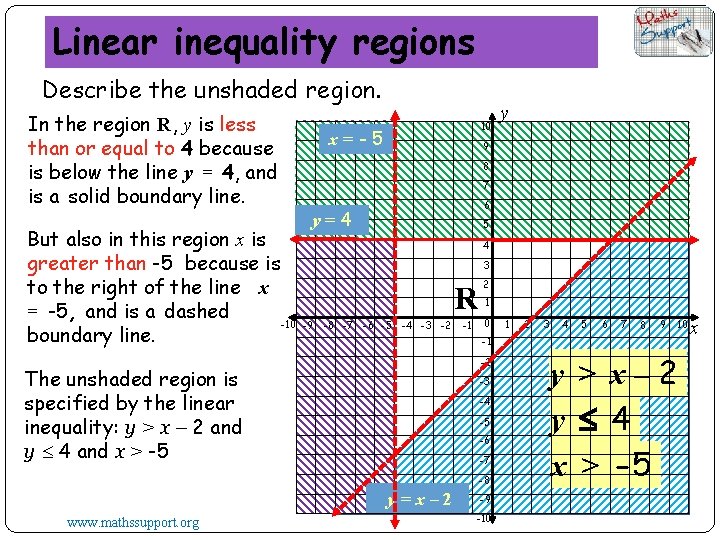
Linear inequality regions Describe the unshaded region. In the region R, y is less than or equal to 4 because is below the line y = 4, and is a solid boundary line. But also in this region x is greater than -5 because is to the right of the line x = -5, and is a dashed -10 boundary line. 10 x=-5 9 8 7 6 y=4 5 4 3 -9 -8 -7 -6 -5 -4 -3 -2 R 2 -1 0 1 1 2 3 4 5 6 7 8 9 -1 -2 The unshaded region is specified by the linear inequality: y > x – 2 and y 4 and x > -5 -3 -4 -5 -6 -7 -8 y=x– 2 www. mathssupport. org y -9 -10 y > x– 2 y 4 x > -5 10 x

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www. mathssupport. org