Feature Extractor Dima Chirkin LBNL Presented by Tom

Feature Extractor Dima Chirkin, LBNL Presented by Tom Mc. Cauley

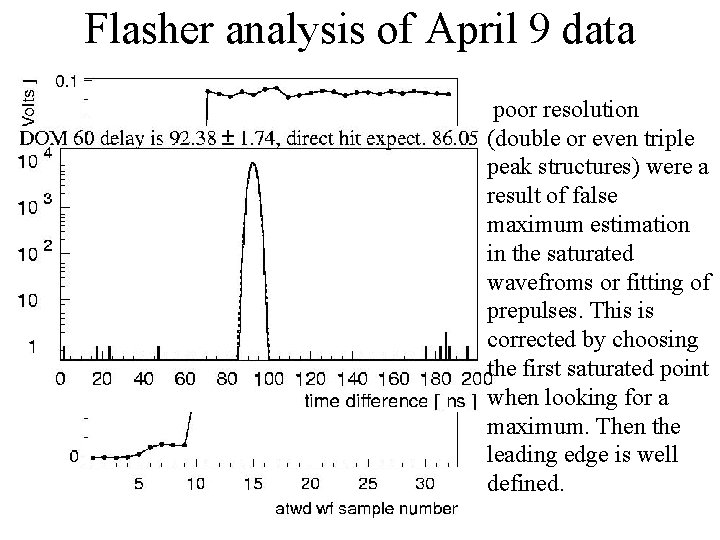
Flasher analysis of April 9 data poor resolution (double or even triple peak structures) were a result of false maximum estimation in the saturated wavefroms or fitting of prepulses. This is corrected by choosing the first saturated point when looking for a maximum. Then the leading edge is well defined.

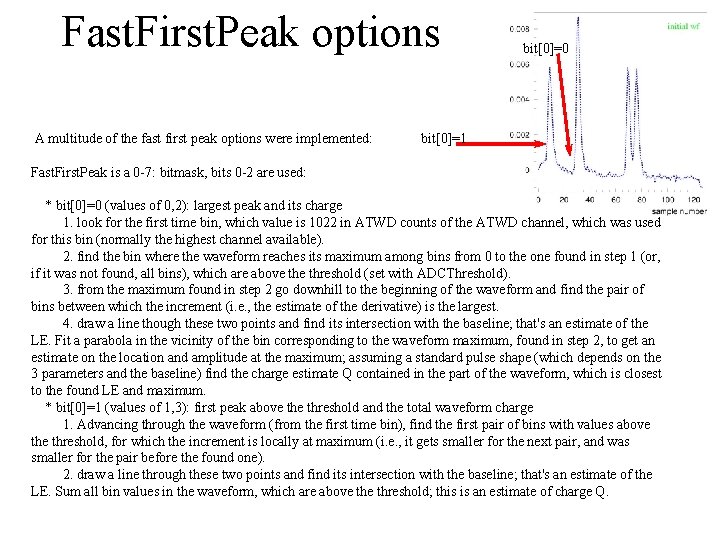
Fast. First. Peak options A multitude of the fast first peak options were implemented: bit[0]=0 bit[0]=1 Fast. First. Peak is a 0 -7: bitmask, bits 0 -2 are used: * bit[0]=0 (values of 0, 2): largest peak and its charge 1. look for the first time bin, which value is 1022 in ATWD counts of the ATWD channel, which was used for this bin (normally the highest channel available). 2. find the bin where the waveform reaches its maximum among bins from 0 to the one found in step 1 (or, if it was not found, all bins), which are above threshold (set with ADCThreshold). 3. from the maximum found in step 2 go downhill to the beginning of the waveform and find the pair of bins between which the increment (i. e. , the estimate of the derivative) is the largest. 4. draw a line though these two points and find its intersection with the baseline; that's an estimate of the LE. Fit a parabola in the vicinity of the bin corresponding to the waveform maximum, found in step 2, to get an estimate on the location and amplitude at the maximum; assuming a standard pulse shape (which depends on the 3 parameters and the baseline) find the charge estimate Q contained in the part of the waveform, which is closest to the found LE and maximum. * bit[0]=1 (values of 1, 3): first peak above threshold and the total waveform charge 1. Advancing through the waveform (from the first time bin), find the first pair of bins with values above threshold, for which the increment is locally at maximum (i. e. , it gets smaller for the next pair, and was smaller for the pair before the found one). 2. draw a line through these two points and find its intersection with the baseline; that's an estimate of the LE. Sum all bin values in the waveform, which are above threshold; this is an estimate of charge Q.

Fast multi-peak algorithm • Existing multi-peak algorithm is excruciatingly slow: processing complicated events (e. g. , flasher) is minutes per event. Goal is : milliseconds • Only SPE-like pulses are found, if pulses are wide (possible with the default settings), then distribution of PEs within SPElike pulses is unknown (current implementation uses heuristics) • Want to have a sub-nanosecond leading edge resolution • is it too much to ask? NO

Waveform unfolding algorithm Spectrum unfolding has been used since last century, why not unfold waveforms? We have a smearing function For each PE we get a pulse like this, so the unfolded data should be a collection of delta functions at the PE leading edges • Bayesian unfolding is selected for its speed and simplicity of implementation and visual step-to-step variance control

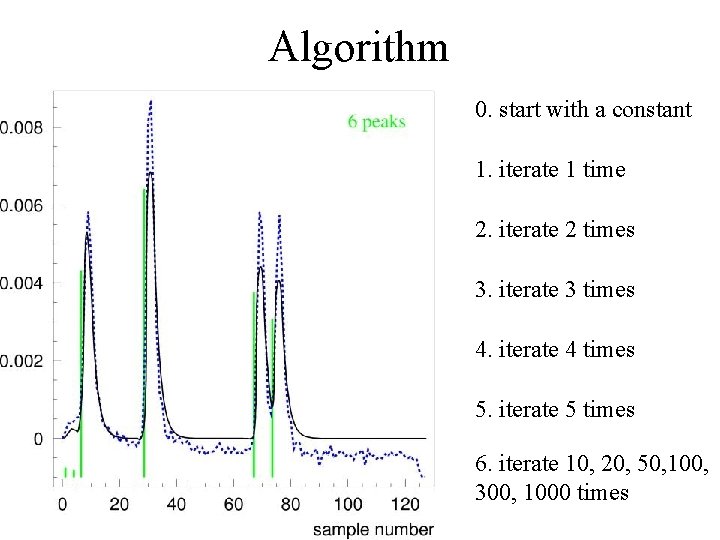
Algorithm 0. start with a constant 1. iterate 1 time 2. iterate 2 times 3. iterate 3 times 4. iterate 4 times 5. iterate 5 times 6. iterate 10, 20, 50, 100, 300, 1000 times

Algorithm • after ~20 -50 steps the result of unfolding stabilizes • The total charge is conserved by the algorithm, it is just being pushed up to the front of the pulse, eventually shrinking it to only one (or 2, see next bullet) bins • the leading edges are on the bin boundaries; this is ~ 3 -4 ns precision. It is possible to refine this. If a fitted pulse does not start on the boundary, then it is approximated by a superposition of 2 pulses. The weighted average of these pulses gives the estimate of the leading edge. The sum of their charges gives the estimate of the charge • Result of the Fast. First. Peak is assigned to the peak, which leading edge is closest to it

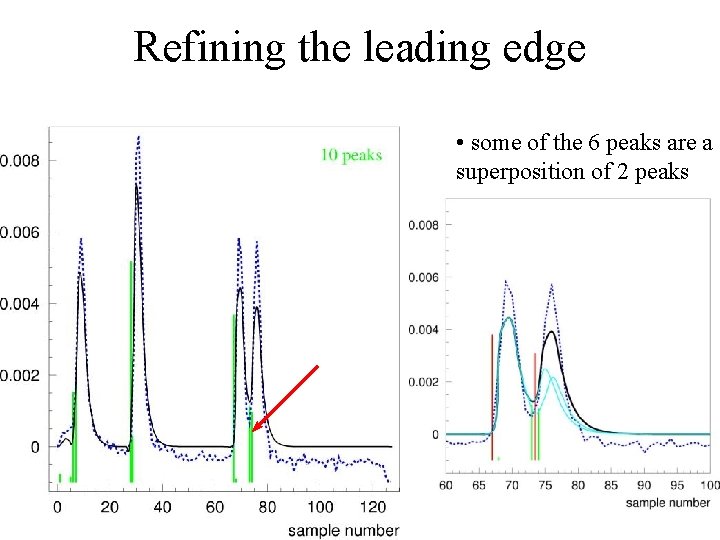
Refining the leading edge • some of the 6 peaks are a superposition of 2 peaks

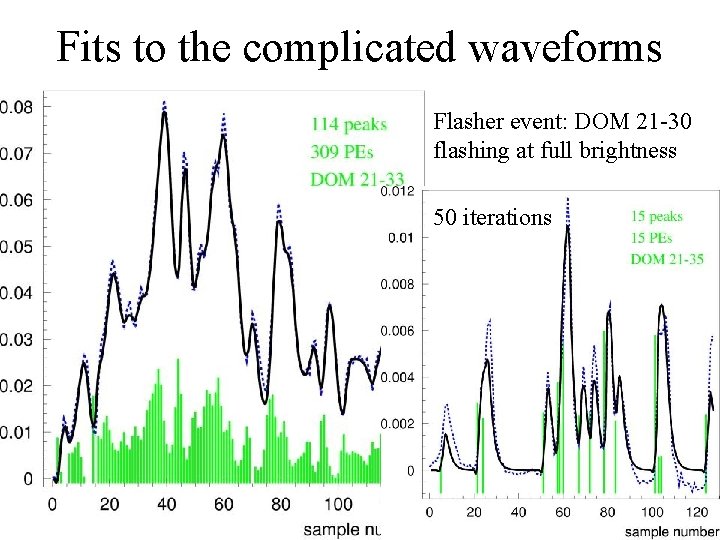
Fits to the complicated waveforms Flasher event: DOM 21 -30 flashing at full brightness 20 iterations 50

Summary of the new alrorithm • Processing of flasher events on pub 2 is now ~60 ms per event (on average 3 ms per waveform) at 20 interations • With the root fits it was ~30 seconds per event (1 second per waveform) • PEs are distributed by the algorithm, no heuristics is necessary • possibly DOM-to-DOM calibration of the algorithm is necessary (to calculate default smearing function width) • can be used in hybrid mode together with the root fit for simple waveforms • sub-nanosecond precision is possible

Conclusions • Feature. Extractor was substantially updated since Berkeley meeting • April flasher timing problems repaired • new Fast. First. Peak options exist • A new very efficient algorithm based on Bayesian unfolding was developed, will appear in the code repository shortly. • Operation is possible in the mixed mode, where simple single and multi-PE waveforms are fitted by root fits, while complicated multi-PE waveforms are fitted by the unfolding algorithm