FConduction transitoire dans un solide semi infini Cas

FConduction transitoire dans un solide semi -infini Cas #1 Surface à température constante Ts t Ti x

Avec les conditions suivantes: t=0 T = Ti à x=0 T = TS à à x= ∞ T = Ti

Pour résoudre on utilise la théorie de la similarité. 2 variables 1 variable On appelle solution de similarité une solution pour laquelle la dépendance de deux variables (x et y) peut se réduire à celle d’une seule variable η par l’application d’une transformation de similarité adéquate. Exemple:

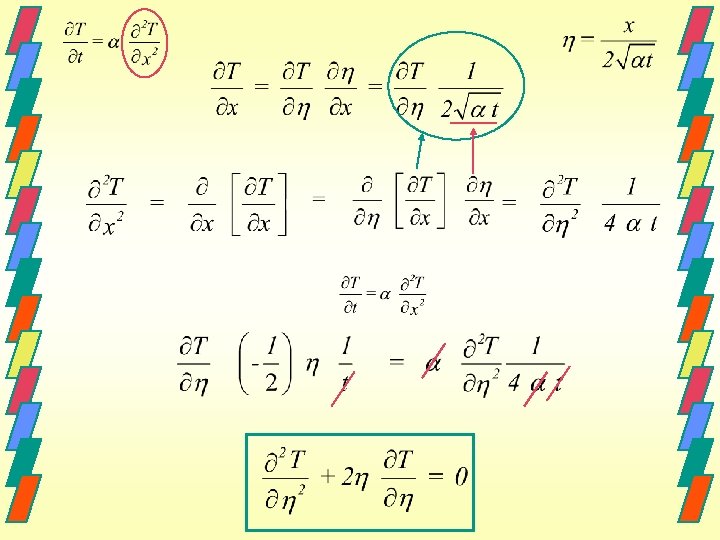
Application de la théorie de la similarité:

Conditions frontière et initiale:

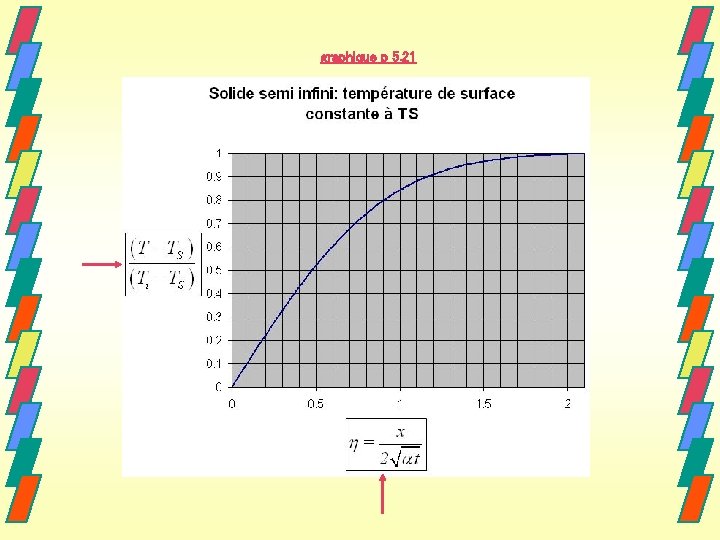
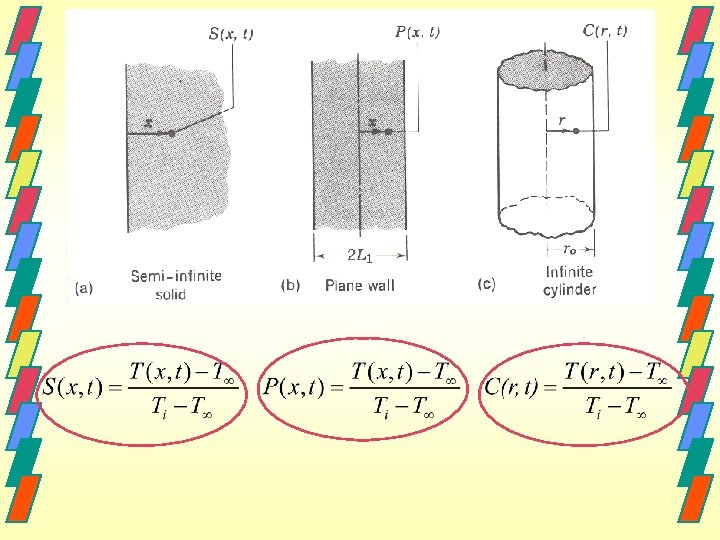
Fonction erreur Avec les CF: (Voir graphique p 5. 21)

graphique p 5. 21

Cas d’une surface avec flux constant Dans le cas où la surface est soumise à un flux constant q 0", la solution T(x, t) est alors: * où erfc z est la fonction erreur complémentaire = 1 - erf z.

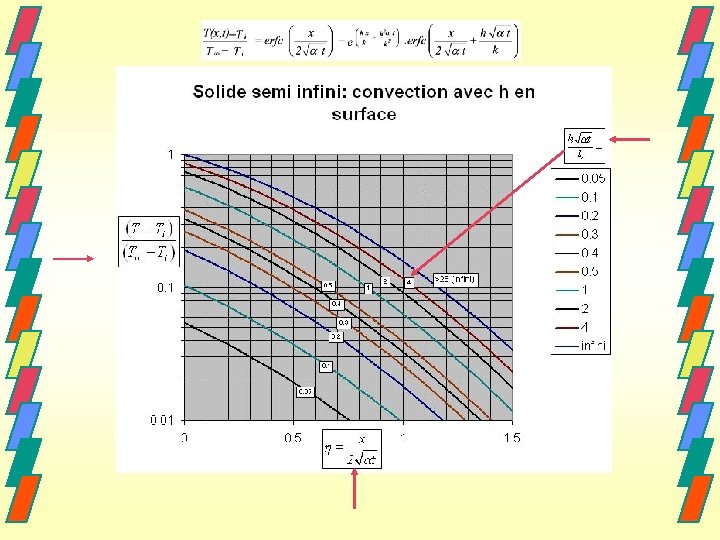
Cas d’une surface avec convection Si la surface est soumise à une convection avec un coefficient h et une température environnante T , l'expression de la température est: (voir la solution graphique) Remarque En pratique, on utilisera les solutions pour un milieu semi -infini quand le transfert de chaleur est limité à une faible épaisseur du matériau considéré (loin de la surface. . . c'est l'infini).

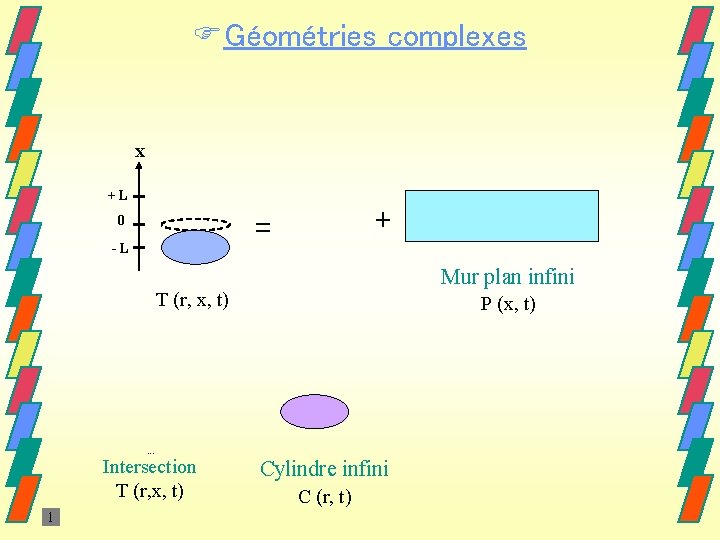
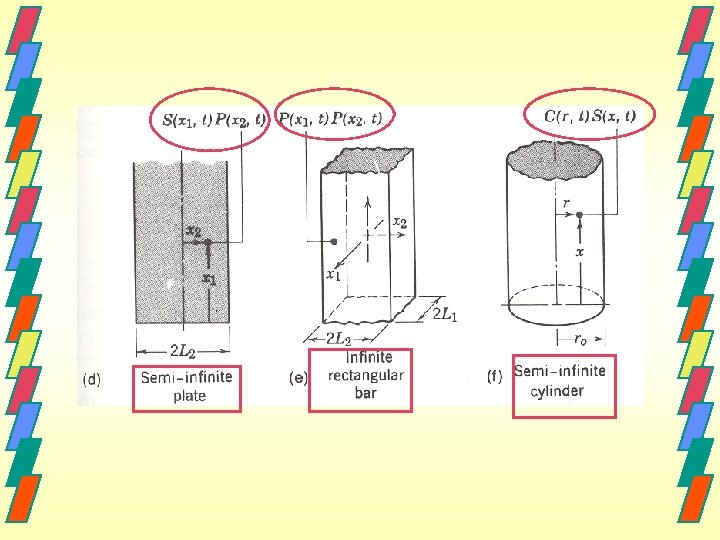
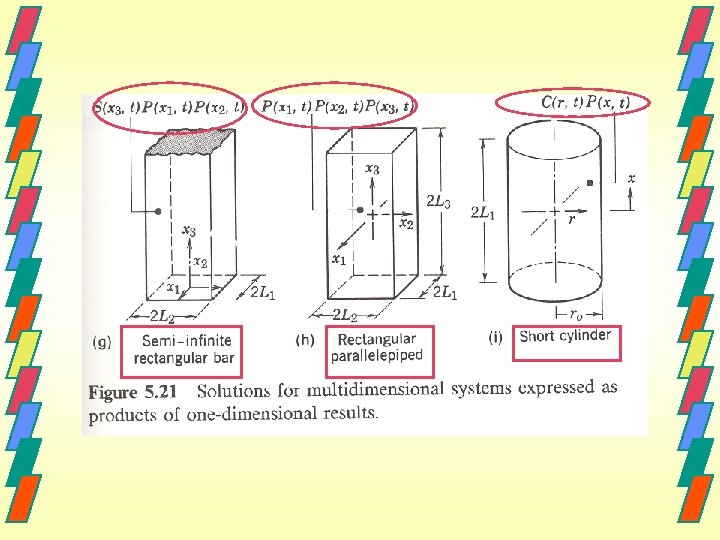
FGéométries complexes x +L + = 0 -L Mur plan infini T (r, x, t) P (x, t) Intersection T (r, x, t) 1 Cylindre infini C (r, t)

Vérifions que T est solution au problème ?

1 ? 2 L’équation est vérifiée car 1 = 0 puisque C est solution de l’équation différentielle pour un cyclindre 2 = 0 puisque P est solution de l’équation différentielle pour un plan * T = C P est alors bien solution. Ainsi on peut appliquer ce principe à différentes formes …

FRésolution par différences finies en transitoire Méthode: On discrétise l'espace (comme en stationnaire) un maillage (convention Ein), On discrétise le temps: 0 t 0, Δt, 2Δt, . . . , nΔt ** Choix d’un « petit » intervalle de temps,

On fait le bilan de chaleur sur un intervalle de temps (Δt) dans le volume autour de chaque nœud n, Si on exprime (∑Ein) à t : Méthode explicite Si on exprime (∑ Ein) à t + Δt : Méthode implicite

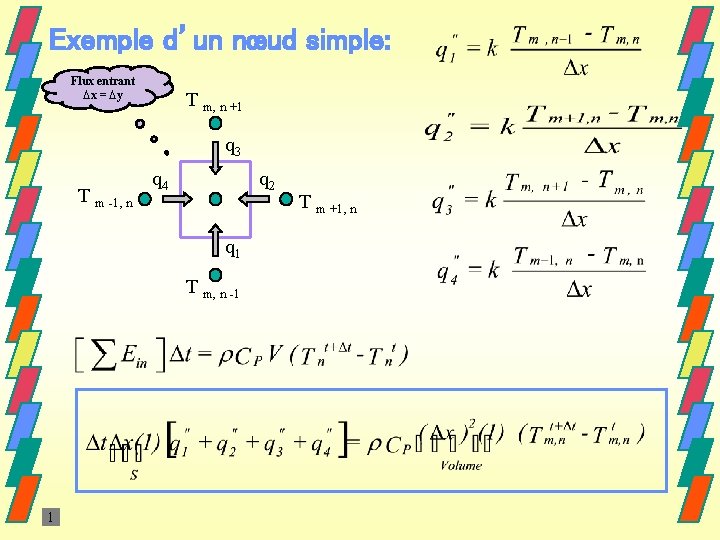
Exemple d’un nœud simple: Flux entrant ∆x = ∆y T m, n +1 q 3 T m -1, n q 4 q 2 q 1 T m, n -1 1 T m +1, n

Méthode explicite On va exprimer les q’’i en utilisant les températures au temps (t) * Si on connaît les températures à t, alors on peut facilement calculer la température à t + Δt. Calcul direct Procédure numérique: On part à t = 0 (toutes les températures étant connues), à t + Δt on utilise la formule précédente puis on avance à nouveau de Δt.

En utilisant le nombre de Fourier … On obtient la formule suivante: La méthode explicite n’est pas « inconditionnellement stable » .

Critère de stabilité ou de convergence Si le coefficient (1 – 4 Fo) ≥ 0 Δx étant fixé, il faut un Δt assez petit pour supposer que les q’’ ne varient pas trop durant dt Exemple 100 °C 50 °C 100 °C ?

Méthode implicite On exprime les flux en fonction des T t + Δt t + Δt

Méthode implicite On exprime les flux en fonction des T t + Δt. * La méthode implicite ne permet pas de calculer directement On fait les bilans sur tous les nœuds et on obtient un système d’équations linéaires. T t : connue T t + Δt : inconnue On le résoud, puis on passe au temps suivant nouveau système d’équations … etc.

FHypothèse d’un régime quasi-permanent ou quasi-stationnaire Il peut être parfois avantageux de considérer un régime transitoire comme une succession de régimes permanents. Il faut que la variation dans le temps d’une variable soit lente par rapport aux autres variations.