FaultTolerant Computing Basic Concepts and Tools Oct 2007

Fault-Tolerant Computing Basic Concepts and Tools Oct. 2007 Terminology, Models, and Measures 1

About This Presentation This presentation has been prepared for the graduate course ECE 257 A (Fault-Tolerant Computing) by Behrooz Parhami, Professor of Electrical and Computer Engineering at University of California, Santa Barbara. The material contained herein can be used freely in classroom teaching or any other educational setting. Unauthorized uses are prohibited. © Behrooz Parhami Oct. 2007 Edition Released Revised First Oct. 2006 Oct. 2007 Terminology, Models, and Measures Revised 2

Terminology, Models, and Measures for Dependability Oct. 2007 Terminology, Models, and Measures 3

Oct. 2007 Terminology, Models, and Measures 4

Fl aw Impairments to Dependability Error a F Oct. 2007 e r ilu Fa Hazard ul Bu g t De n o i t a grad Intr usio n t c efe Ma D lfu Crash Terminology, Models, and Measures nc tio n 5

The Fault-Error-Failure Cycle Includes both components and design 0 Correct signal 0 0 Fault Replaced with NAND? Schematic diagram of the Newcastle hierarchical model and the impairments within one level. Oct. 2007 Terminology, Models, and Measures 6

The Four-Universe Model Cause-effect diagram for Avižienis’ four-universe model of impairments to dependability. Oct. 2007 Terminology, Models, and Measures 7
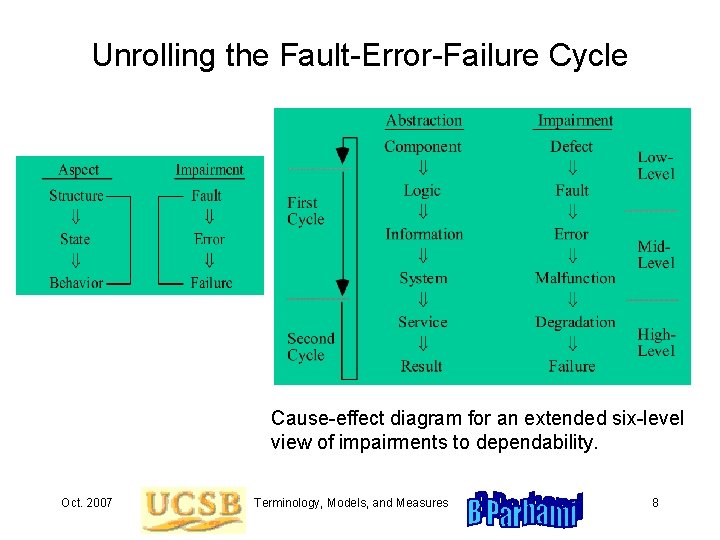
Unrolling the Fault-Error-Failure Cycle Cause-effect diagram for an extended six-level view of impairments to dependability. Oct. 2007 Terminology, Models, and Measures 8
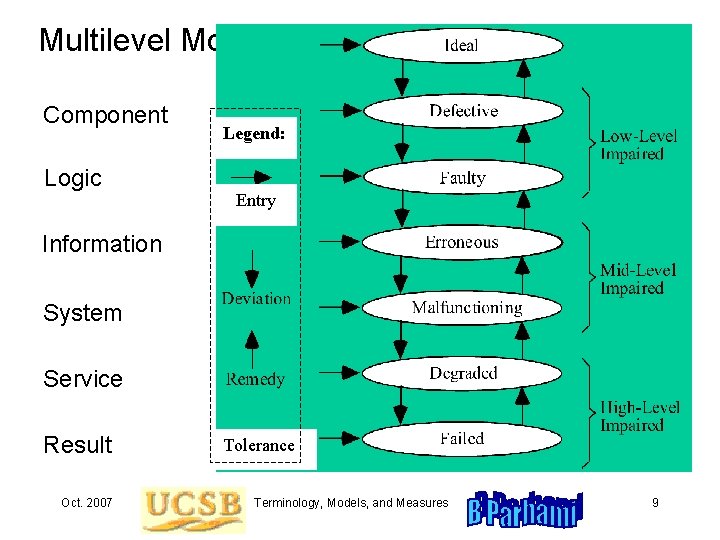
Multilevel Model Component Logic Legend: Entry Information System Service Result Oct. 2007 Tolerance Terminology, Models, and Measures 9
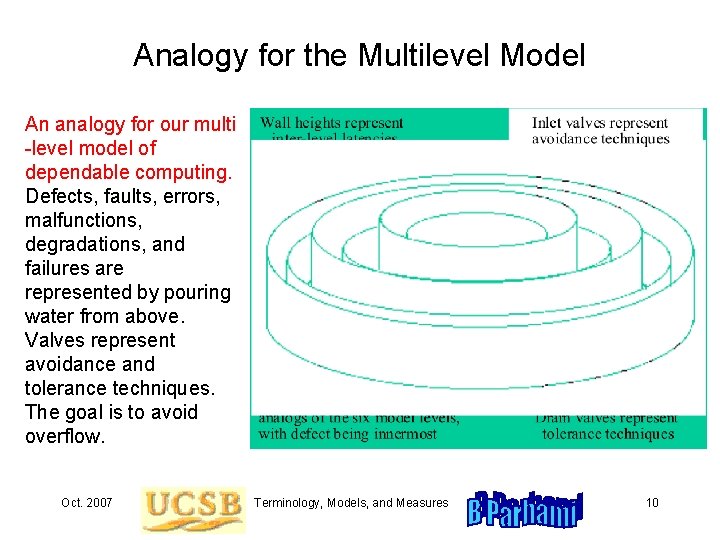
Analogy for the Multilevel Model An analogy for our multi -level model of dependable computing. Defects, faults, errors, malfunctions, degradations, and failures are represented by pouring water from above. Valves represent avoidance and tolerance techniques. The goal is to avoid overflow. Oct. 2007 Terminology, Models, and Measures 10
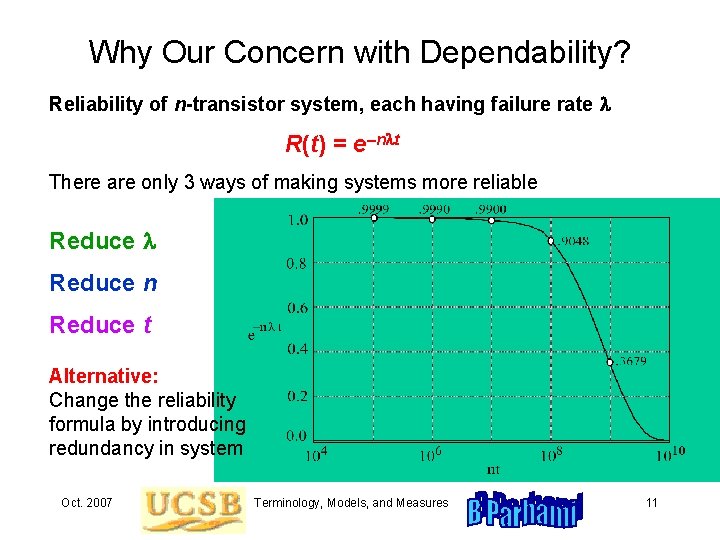
Why Our Concern with Dependability? Reliability of n-transistor system, each having failure rate l R(t) = e–nlt There are only 3 ways of making systems more reliable Reduce l Reduce n Reduce t Alternative: Change the reliability formula by introducing redundancy in system Oct. 2007 Terminology, Models, and Measures 11

Highly Dependable Computer Systems Long-life systems: Fail-slow, Rugged, High-reliability Spacecraft with multiyear missions, systems in inaccessible locations Methods: Replication (spares), error coding, monitoring, shielding Safety-critical systems: Fail-safe, Sound, High-integrity Flight control computers, nuclear-plant shutdown, medical monitoring Methods: Replication with voting, time redundancy, design diversity Non-stop systems: Fail-soft, Robust, High-availability Telephone switching centers, transaction processing, e-commerce Methods: HW/info redundancy, backup schemes, hot-swap, recovery Just as performance enhancement techniques gradually migrate from supercomputers to desktops, so too dependability enhancement methods find their way from exotic systems into personal computers Oct. 2007 Terminology, Models, and Measures 12

Aspects of Dependability ea c i rv bi y t li y qu t e fe ns Se Se Reliability. MTTF = MTFF Reliabili ce n e ty, il ty a co , S k cu rit Ri y s li ityerva b nt I a , . il av a ise TR v A tw T in , M o P BF MT Resilience y t i l bi ty, . , v la Ma int a ili t b es rolla ility T nt vab o C ser ob i BF b ain a, MC Ro ab mlity Inte r b ust i o l g bi ity f r a n i r t y e m r ss e o f P er P Oct. 2007 Terminology, Models, and Measures 13
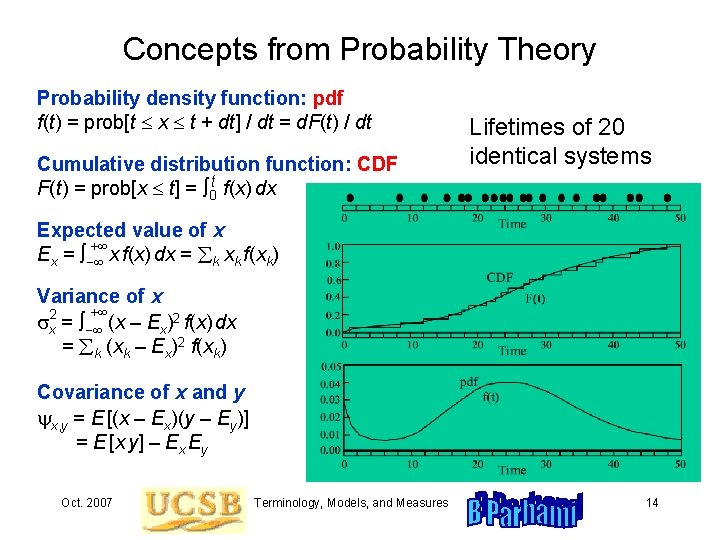
Concepts from Probability Theory Probability density function: pdf f(t) = prob[t x t + dt] / dt = d. F(t) / dt Cumulative distribution function: CDF F(t) = prob[x t] = 0 t f(x) dx Lifetimes of 20 identical systems Expected value of x + Ex = - x f(x) dx = k xk f(xk) Variance of x + 2 sx = - (x – Ex)2 f(x) dx = k (xk – Ex)2 f(xk) Covariance of x and y yx, y = E [(x – Ex)(y – Ey)] = E [x y] – Ex Ey Oct. 2007 Terminology, Models, and Measures 14
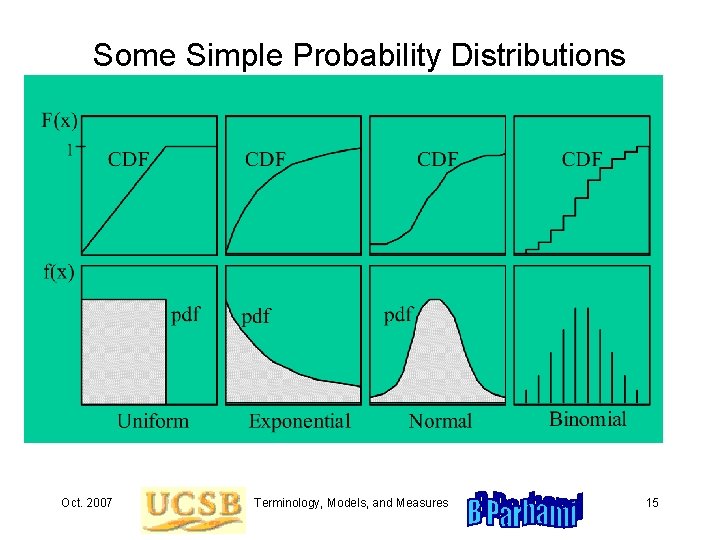
Some Simple Probability Distributions Oct. 2007 Terminology, Models, and Measures 15

Reliability and MTTF Reliability: R(t) Probability that system remains in the “Good” state through the interval [0, t] Two-state nonrepairable system R(t + dt) = R(t) [1 – z(t) dt] Hazard function R(t) = 1 – F(t) Start state Failure Down CDF of the system lifetime, or its unreliability Constant hazard function z(t) = l R(t) = e–lt (system failure rate is independent of its age) Mean time to failure: MTTF + + MTTF = 0 t f(t) dt = 0 R(t) dt Expected value of lifetime Oct. 2007 Up Exponential reliability law Area under the reliability curve (easily provable) Terminology, Models, and Measures 16

Failure Distributions of Interest Exponential: z(t) = l R(t) = e–lt MTTF = 1/l Discrete versions Geometric R(k) = q k Rayleigh: z(t) = 2 l(lt) R(t) = e(-lt)2 MTTF = (1/l) p / 2 Weibull: z(t) = al(lt) a– 1 R(t) = e(-lt)a MTTF = (1/l) G(1 + 1/a) Discrete Weibull Erlang: MTTF = k/l Gamma: Erlang and exponential are special cases Normal: Reliability and MTTF formulas are complicated Oct. 2007 Terminology, Models, and Measures Binomial 17
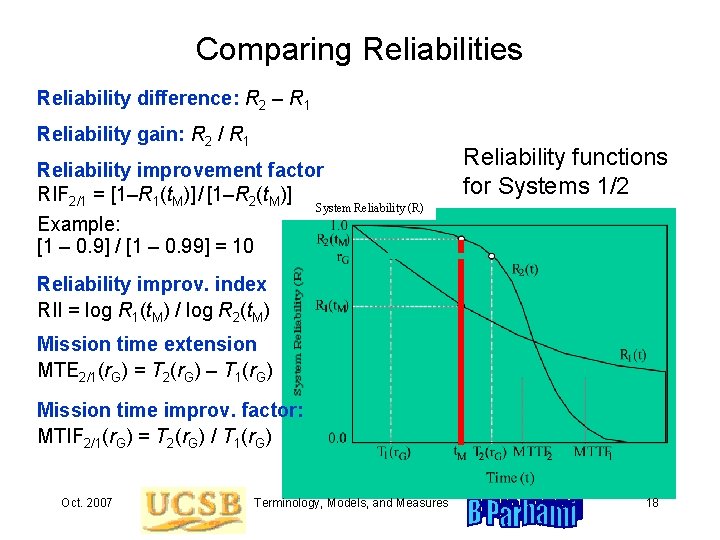
Comparing Reliabilities Reliability difference: R 2 – R 1 Reliability gain: R 2 / R 1 Reliability improvement factor RIF 2/1 = [1–R 1(t. M)] / [1–R 2(t. M)] Example: [1 – 0. 9] / [1 – 0. 99] = 10 Reliability functions for Systems 1/2 System Reliability (R) Reliability improv. index RII = log R 1(t. M) / log R 2(t. M) Mission time extension MTE 2/1(r. G) = T 2(r. G) – T 1(r. G) Mission time improv. factor: MTIF 2/1(r. G) = T 2(r. G) / T 1(r. G) Oct. 2007 Terminology, Models, and Measures 18

Availability, MTTR, and MTBF (Interval) Availability: A(t) Fraction of time that system is in the “Up” state during the interval [0, t] Two-state repairable system Steady-state availability: A = limt A(t) Pointwise availability: a(t) Probability that system available at time t A(t) = (1/t) 0 t a(x) dx Repair Start state Up Down Failure Availability = Reliability, when there is no repair Availability is a function not only of how rarely a system fails (reliability) but also of how quickly it can be repaired (time to repair) Repair rate MTTF m A= = = 1/m = MTTR MTTF + MTTR MTBF l+m In general, m >> l, leading to A 1 Oct. 2007 Terminology, Models, and Measures (Will justify this equation later) 19
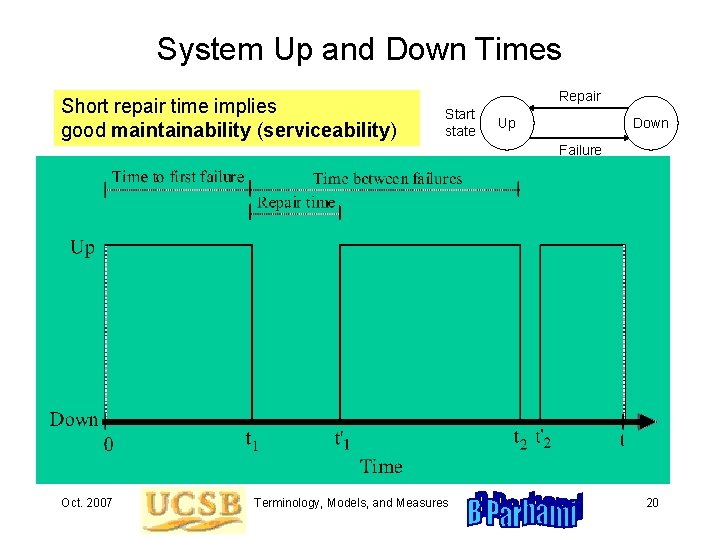
System Up and Down Times Short repair time implies good maintainability (serviceability) Repair Start state Up Down Failure Oct. 2007 Terminology, Models, and Measures 20
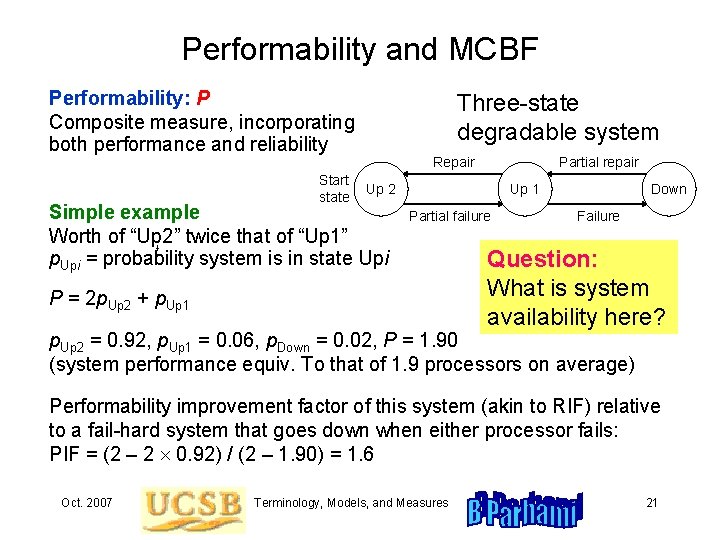
Performability and MCBF Performability: P Composite measure, incorporating both performance and reliability Start state Three-state degradable system Repair Partial repair Up 2 Simple example Worth of “Up 2” twice that of “Up 1” t p. Upi = probability system is in state Upi Up 1 Partial failure P = 2 p. Up 2 + p. Up 1 Down Failure Question: What is system availability here? p. Up 2 = 0. 92, p. Up 1 = 0. 06, p. Down = 0. 02, P = 1. 90 (system performance equiv. To that of 1. 9 processors on average) Performability improvement factor of this system (akin to RIF) relative to a fail-hard system that goes down when either processor fails: PIF = (2 – 2 0. 92) / (2 – 1. 90) = 1. 6 Oct. 2007 Terminology, Models, and Measures 21
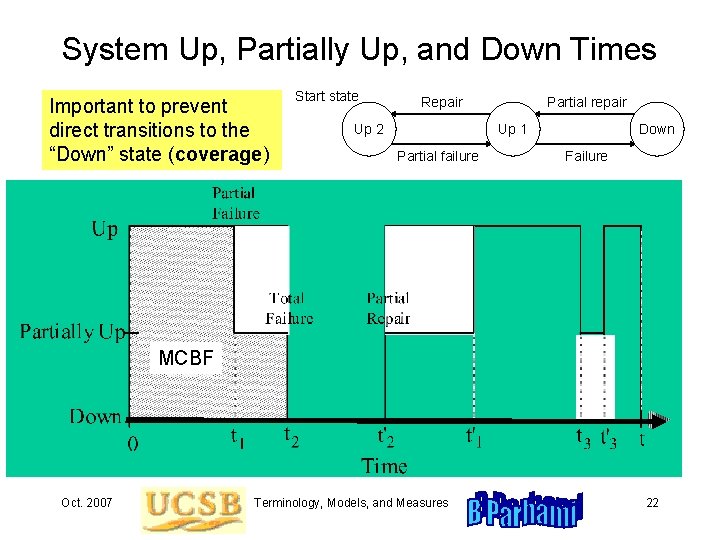
System Up, Partially Up, and Down Times Important to prevent direct transitions to the “Down” state (coverage) Start state Repair Up 2 Partial repair Up 1 Partial failure Down Failure MCBF Oct. 2007 Terminology, Models, and Measures 22
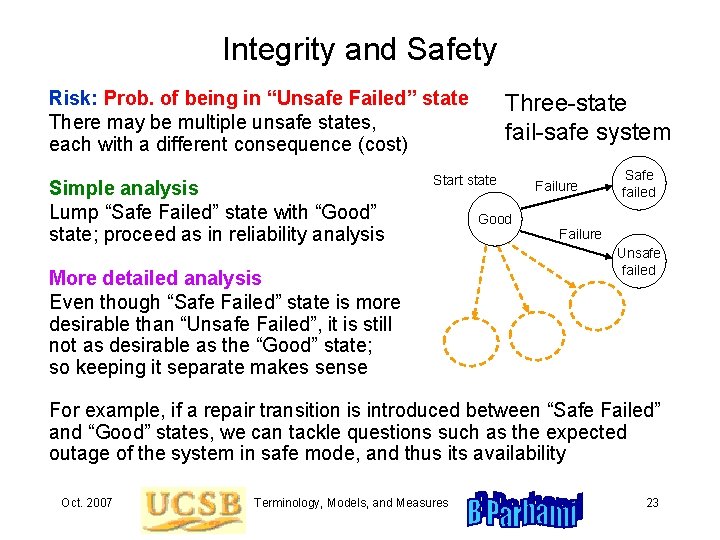
Integrity and Safety Risk: Prob. of being in “Unsafe Failed” state There may be multiple unsafe states, each with a different consequence (cost) Simple analysis Lump “Safe Failed” state with “Good” state; proceed as in reliability analysis Three-state fail-safe system Start state More detailed analysis Even though “Safe Failed” state is more desirable than “Unsafe Failed”, it is still not as desirable as the “Good” state; so keeping it separate makes sense Good Failure Safe failed Failure Unsafe failed For example, if a repair transition is introduced between “Safe Failed” and “Good” states, we can tackle questions such as the expected outage of the system in safe mode, and thus its availability Oct. 2007 Terminology, Models, and Measures 23
- Slides: 23