Fat Tail Distributions and Efficiency of Flow Processing

Fat Tail Distributions and Efficiency of Flow Processing on Complex Networks Zoltán Toroczkai Center for Nonlinear Studies, and Complex Systems Group, Theoretical Division, Los Alamos National Laboratory LA-UR-03 -5542 LANL LDRD-DR S. P. I. N. Project, 2003 -06

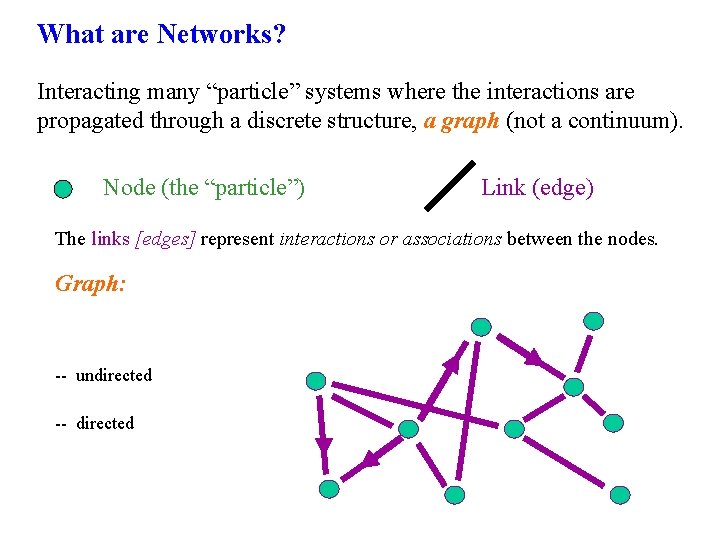
What are Networks? Interacting many “particle” systems where the interactions are propagated through a discrete structure, a graph (not a continuum). Node (the “particle”) Link (edge) The links [edges] represent interactions or associations between the nodes. Graph: -- undirected -- directed

Where are Networks? • Infrastructures: transportation nw-s (airports, highways, roads, rail, water) energy transport nw-s (electric power, petroleum, natural gas) • Communications: telephone, microwave backbone, internet, email, www, etc. • Biology: protein-gene interactions, protein-protein interactions, metabolic nw-s, cell-signaling nw-s, the food web, etc. • Social Systems: acquaintance (friendship) nw-s, terrorist nw-s, collaboration networks, epidemic networks, the sex-web • Geology: river networks

Communication Networks Skitter data depicting a macroscopic snapshot of Internet connectivity, with selected backbone ISPs (Internet Service Provider) colored separately by K. C. Claffy email: kc@caida. org http: //www. caida. org/Papers/Nae/

Networks in Biology The metabolic pathway Chemicals Bio-Chemical reactions

Networks in Biology The metabolic pathway Chemicals Bio-Chemical reactions Biochemical Pathways - Metabolic Pathways, Source: Ex. PASy

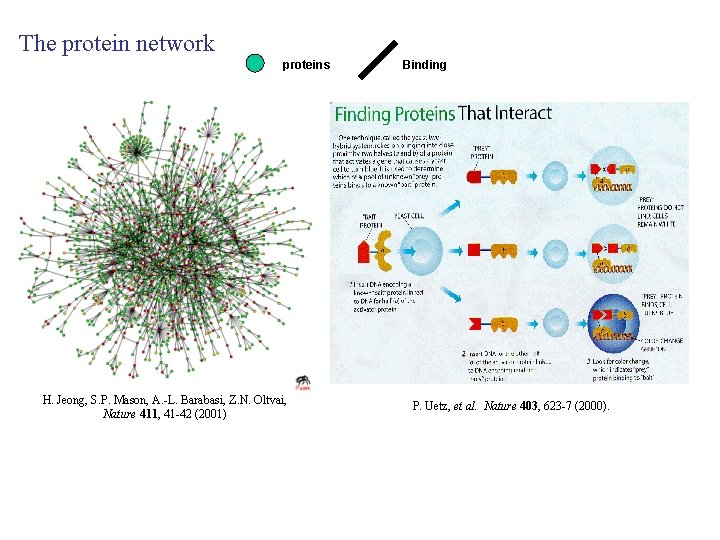
The protein network proteins H. Jeong, S. P. Mason, A. -L. Barabasi, Z. N. Oltvai, Nature 411, 41 -42 (2001) Binding P. Uetz, et al. Nature 403, 623 -7 (2000).

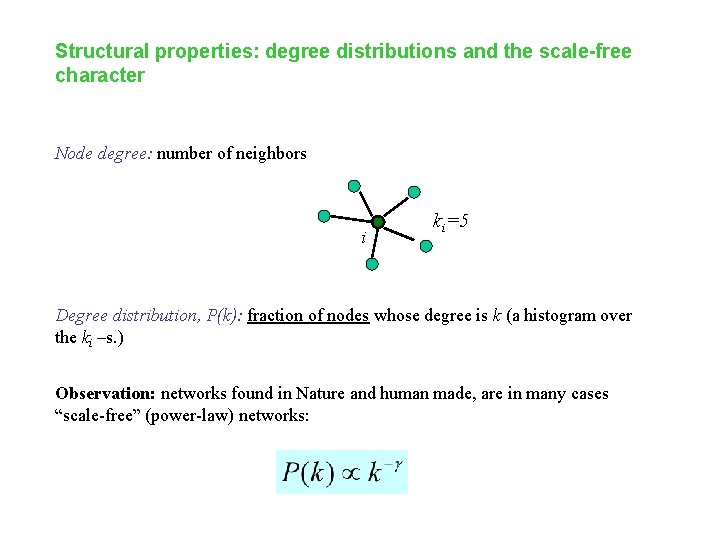
Structural properties: degree distributions and the scale-free character Node degree: number of neighbors i ki=5 Degree distribution, P(k): fraction of nodes whose degree is k (a histogram over the ki –s. ) Observation: networks found in Nature and human made, are in many cases “scale-free” (power-law) networks:

For the sake of definitions: The Erdős-Rényi Random Graph (also called the binomial random graph) • Consider N nodes (dots). • Take every pair (i, j) of nodes and connect them with an edge with probability p.

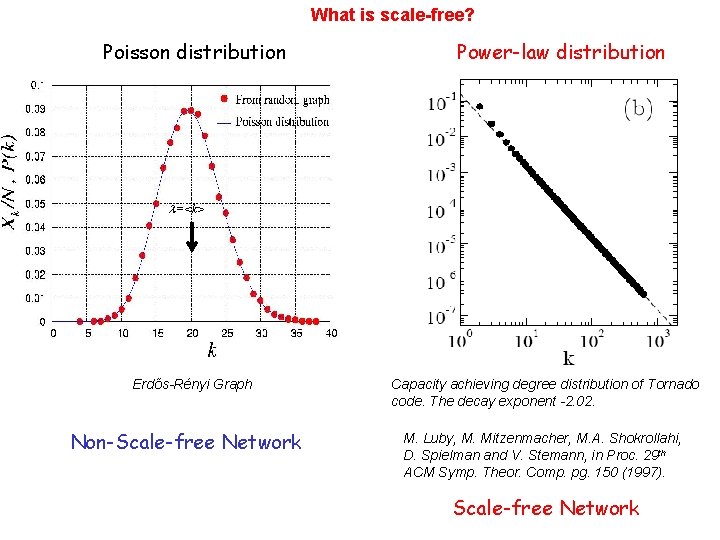
What is scale-free? Poisson distribution Power-law distribution =<k> Erdős-Rényi Graph Non-Scale-free Network Capacity achieving degree distribution of Tornado code. The decay exponent -2. 02. M. Luby, M. Mitzenmacher, M. A. Shokrollahi, D. Spielman and V. Stemann, in Proc. 29 th ACM Symp. Theor. Comp. pg. 150 (1997). Scale-free Network

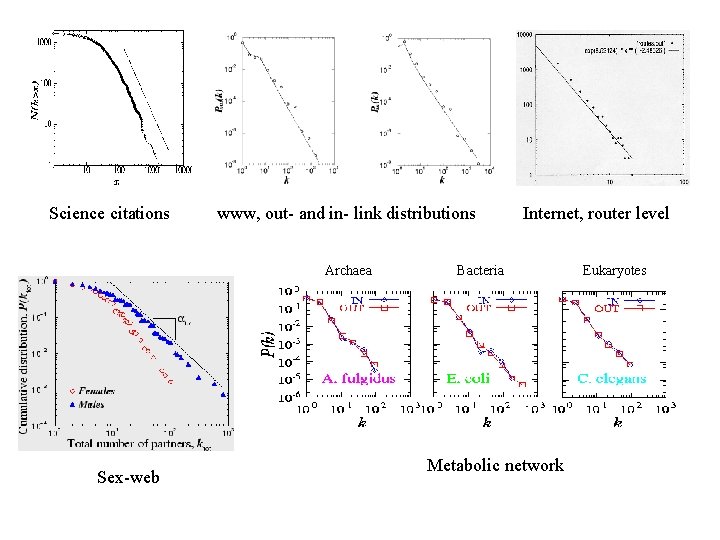
Science citations www, out- and in- link distributions Archaea Bacteria Sex-web Internet, router level Bacteria Eukaryotes Metabolic network Eukaryotes

Scale-free Networks: Coincidence or Universality? • No obvious universal mechanism identified • As a matter of fact we claim that there is none (universal that is). • Instead, our statement is that at least for a large class of networks (to be specified) network structural evolution is governed by a selection principle which is closely tied to the global efficiency of transport and flow processing by these structures, and • Whatever the specific mechanism, it is such as to obey this selection principle. Need to define first a flow process on these networks. Z. Toroczkai and K. E. Bassler, “Jamming is Limited in Scale-free Networks”, Nature, 428, 716 (2004) Z. Toroczkai, B. Kozma, K. E. Bassler, N. W. Hengartner and G. Korniss “Gradient Networks”, http: //www. arxiv. org/cond-mat/0408262

Gradient Flow Networks Gradients of a scalar (temperature, concentration, potential, etc. ) induce flows (heat, particles, currents, etc. ). Naturally, gradients will induce flows on networks as well. Ex. : Load balancing in parallel computation and packet routing on the internet Y. Rabani, A. Sinclair and R. Wanka, Proc. 39 th Symp. On Foundations of Computer Science (FOCS), 1998: “Local Divergence of Markov Chains and the Analysis of Iterative Load-balancing Schemes”

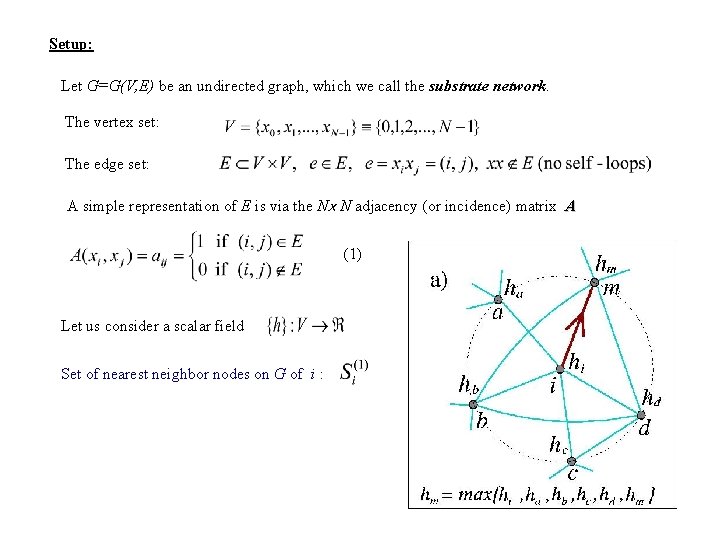
Setup: Let G=G(V, E) be an undirected graph, which we call the substrate network. The vertex set: The edge set: A simple representation of E is via the Nx N adjacency (or incidence) matrix A (1) Let us consider a scalar field Set of nearest neighbor nodes on G of i :

Definition 1 The gradient h(i) of the field {h} in node i is a directed edge: (2) Which points from i to that nearest neighbor for G for which the increase in the scalar is the largest, i. e. , : (3) The weight associated with edge (i, ) is given by: . The self-loop is a loop through i with zero weight. Definition 2 The set F of directed gradient edges on G together with the vertex set V forms the gradient network: If (3) admits more than one solution, than the gradient in i is degenerate.

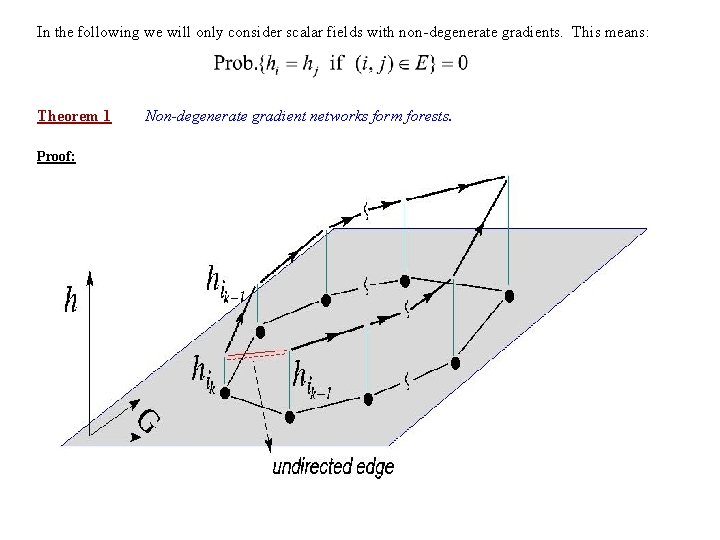
In the following we will only consider scalar fields with non-degenerate gradients. This means: Theorem 1 Proof: Non-degenerate gradient networks form forests.

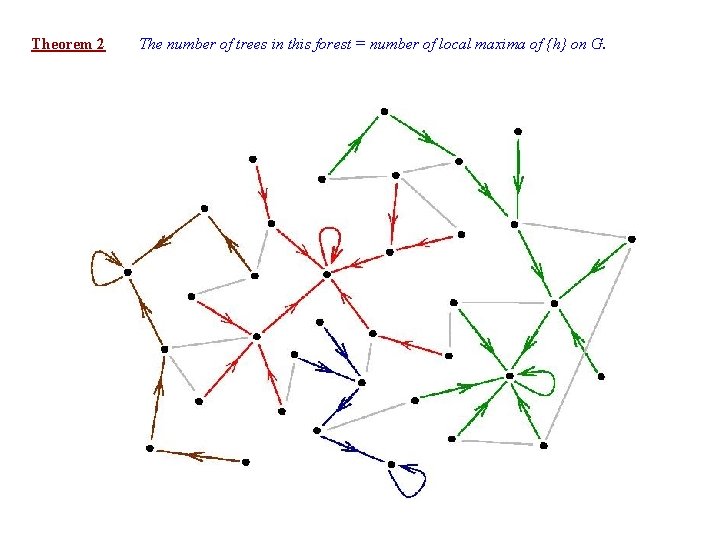
Theorem 2 The number of trees in this forest = number of local maxima of {h} on G.

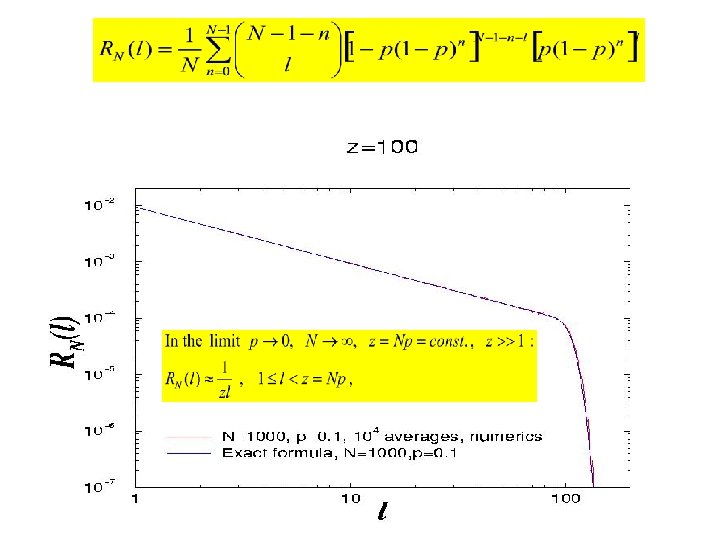
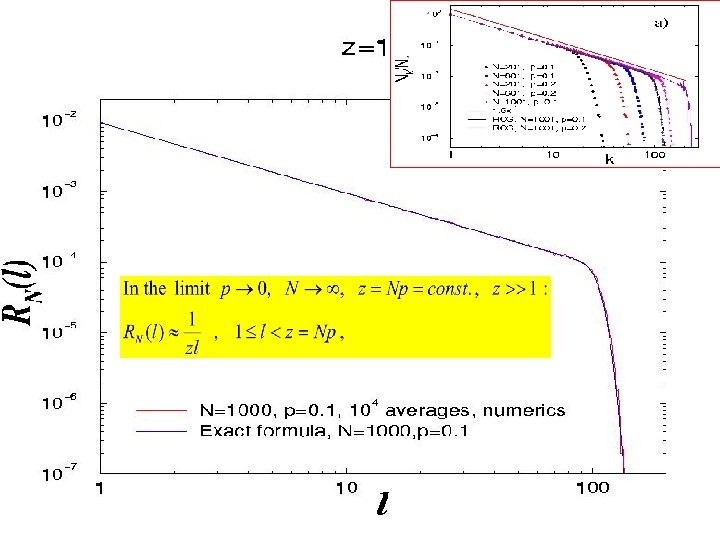
In-degree distribution of the Gradient Network when G=GN, p. A combinatorial derivation Version: Balazs Kozma (RPI) Assume that the scalar values at the nodes are i. i. d, according to some distribution (h). First, distribute the scalars on the node set V, then find those link configurations which contribute to R(l) when building the GN, p graph. Without restricting the generality, calculate R(l) for node 0. Consider the set of nodes with the property Let the number of elements in this set be n, and the set be denoted by [n]. The complementary set of [n] in V{0} is :

In order to have exactly l nodes pointing their gradient edges into 0: • they have to be connected to node 0 on the substrate • they must NOT be connected to the set [n] For l nodes: Also need to require that no other nodes will be pointing their gradient directions into node 0 : (Obviously none of the [n] will. ) So, for a fixed h 0 and a specific set [n] :

The probability Qn for such an event for a given n while letting h-s vary according to their distribution: For one node to have its scalar larger than h 0: For exactly n nodes: Thus: Combining: Finally:

What happens when the substrate is a scale-free network?

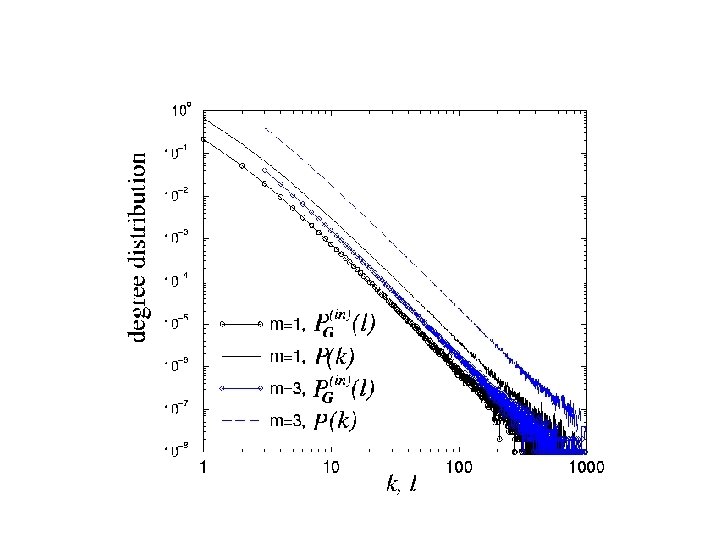
Gradient Networks and Transport Efficiency - every node has exactly one out-link (one gradient direction) but it can have more than one in-link (the followers) - the gradient network has N-nodes and N out-links. So the number of “out-streams” is Nsend = N - the number of RECEIVERS is - J is a congestion (pressure) characteristic. - 0 J 1. J=0: minimum congestion, J=1: maximum congestion

In the scaling limit - for large networks we get maximal congestion! In the scaling limit - becomes congested for large average degree.

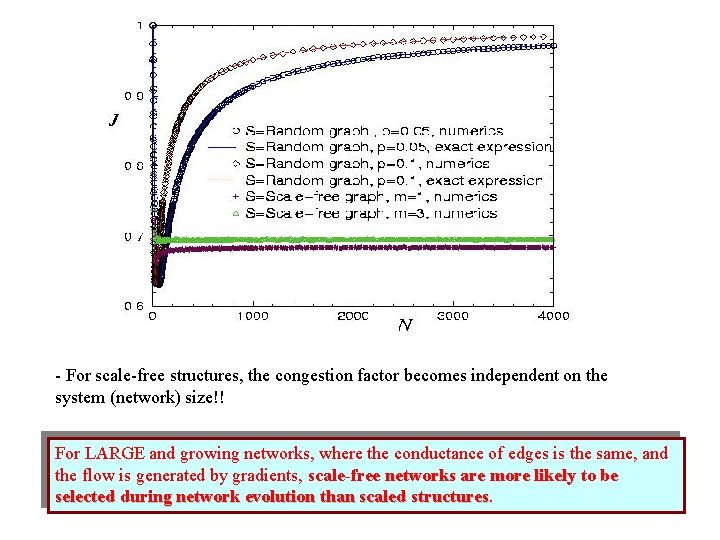
- For scale-free structures, the congestion factor becomes independent on the system (network) size!! For LARGE and growing networks, where the conductance of edges is the same, and the flow is generated by gradients, scale-free networks are more likely to be selected during network evolution than scaled structures

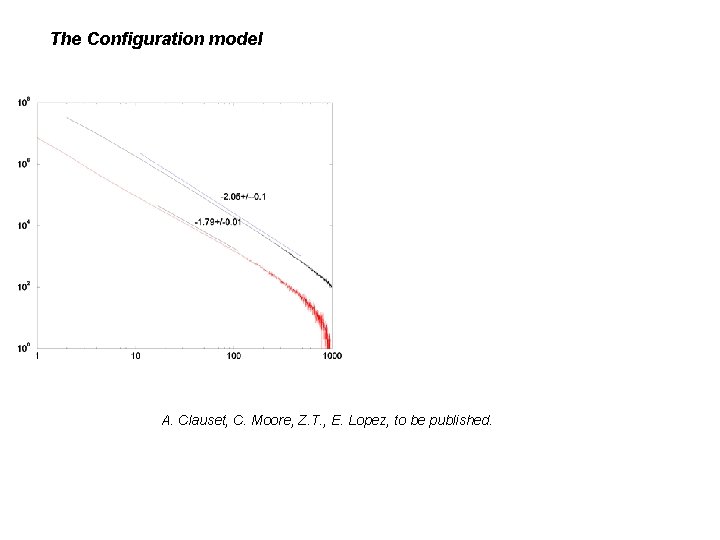
The Configuration model A. Clauset, C. Moore, Z. T. , E. Lopez, to be published.

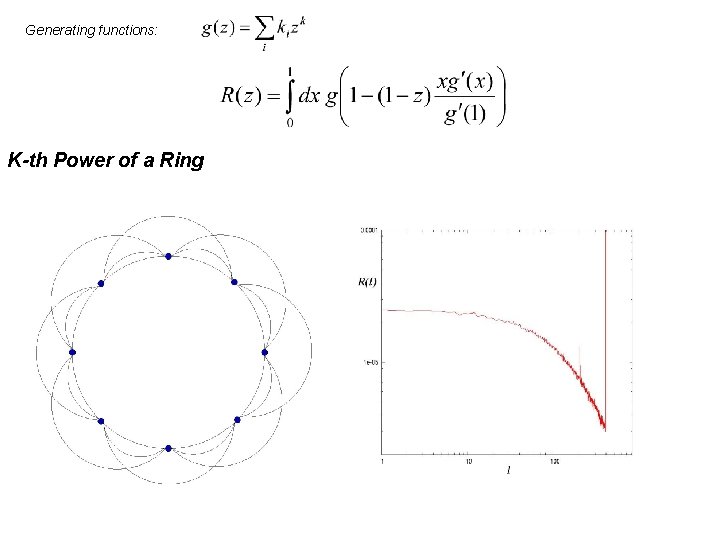
Generating functions: K-th Power of a Ring

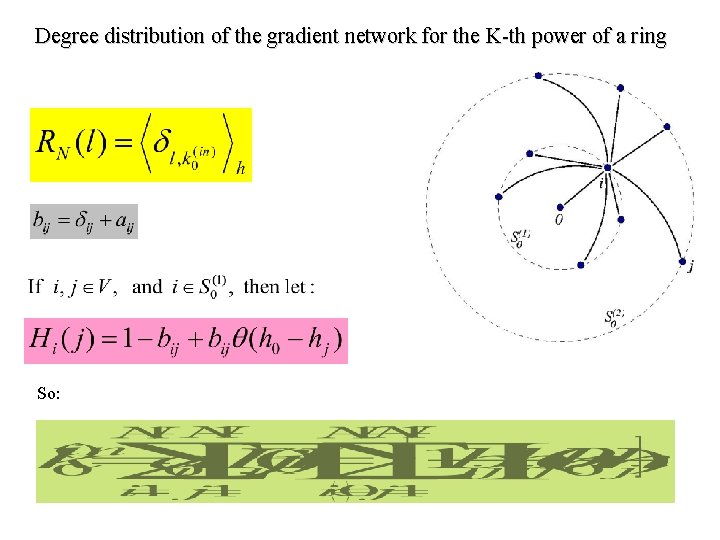
Degree distribution of the gradient network for the K-th power of a ring So:

where is an n-subset of the set {1, 2, …, N-1}. denotes the set of all possible n-subsets of {1, 2…, N-1}. is always zero, if there is a node from the n-subset connected to i, or i belongs to the n-subset. Let which is the union of the disks of all nodes from the n-subset. Thus, one needs to find the number of coverings of the ring with n disks, each of radius K, that misses exactly l nearest neighbors of the origin.

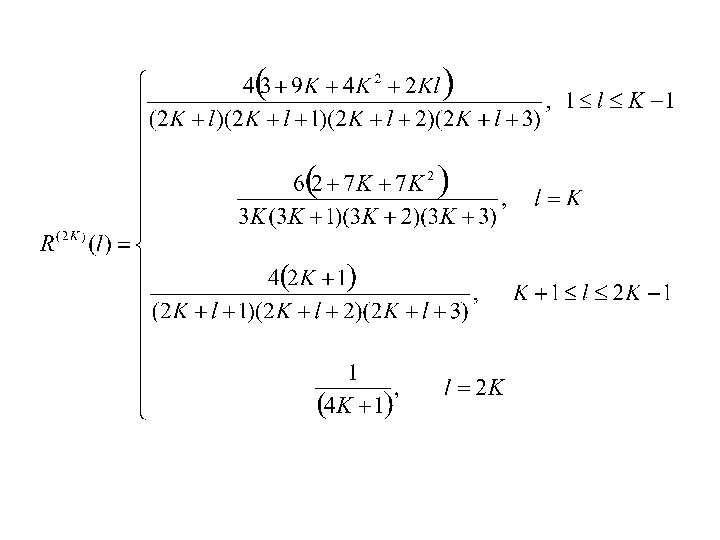
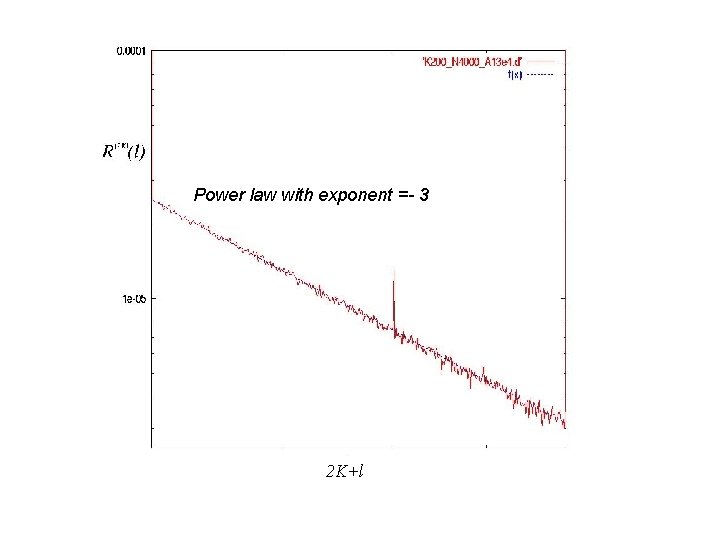
Power law with exponent =- 3 2 K+l

Competition Games on Networks Collaboration with: • Marian Anghel (CCS-3) • Kevin E. Bassler (U. Houston) • György Korniss (Rensselaer) References: M. Anghel, Z. Toroczkai, K. E. Bassler and G. Korniss, Competition-driven Network Dynamics: Emergence of a Scale-free Leadership Structure and Collective Efficiency, Phys. Rev. Lett. 92, 058701 (2004) Z. Toroczkai, M. Anghel, G. Korniss and K. W. Bassler, Effects of Inter-agent Communications on the Collective, in Collectives and the Design of Complex Systems, eds. K. Tumer and D. H. Wolpert, Springer, 2004.

Resource limitations lead in human, and most biological populations to competitive dynamics. The more severe the limitations, the more fierce the competition. Amid competitive conditions certain agents may have better venues or strategies to reach the resources, which puts them into a distinguished class of the “few”, or elites. Elites form a minority group. In spite of the minority character, the elites can considerably shape the structure of the whole society: since they are the most successful (in the given situation), the rest of the agents will tend to follow (imitate, interact with) the elites creating a social structure of leadership in the agent society. Definition: a leader is an agent that has at least one follower at that moment. The influence of a leader is measured by the number of followers it has. Leaders can be following other leaders or themselves. The non-leaders are coined “followers”.

The El Farol bar problem [W. B Arthur(1994)] A B …

A binary (computer friendly) version of the El Farol bar problem: The Minority Game (MG) [Challet and Zhang (1997)] A = “ 0” (bar ok, go to the bar) B = “ 1” (bar crowded, stay home) latest bit (011. . 101) World utility(history): l {0, 1, . . , 2 m-1} m bits (Strategies)(i) = S(i)1(l) S(i)2(l) (Scores)(i) = C (i)(k), k = 1, 2, . . , S. S(i)S(l) (Prediction) (i) =

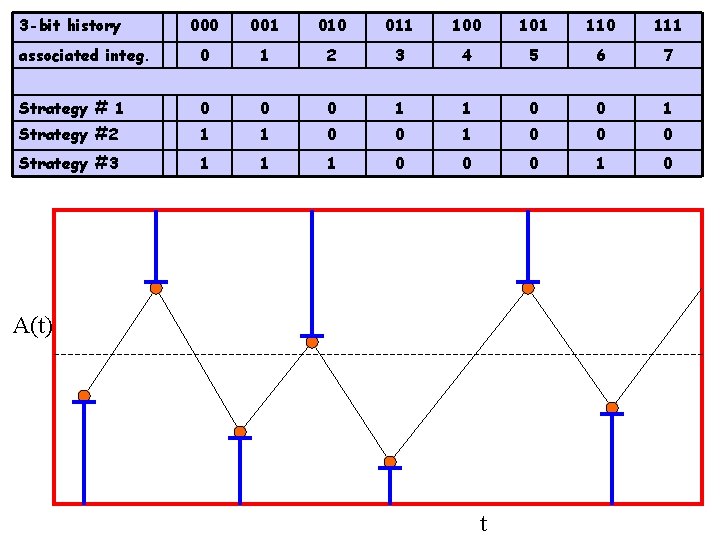
3 -bit history 000 001 010 011 100 101 110 111 associated integ. 0 1 2 3 4 5 6 7 Strategy # 1 0 0 0 1 1 0 0 1 Strategy #2 1 1 0 0 0 Strategy #3 1 1 1 0 0 0 1 0 A(t) t

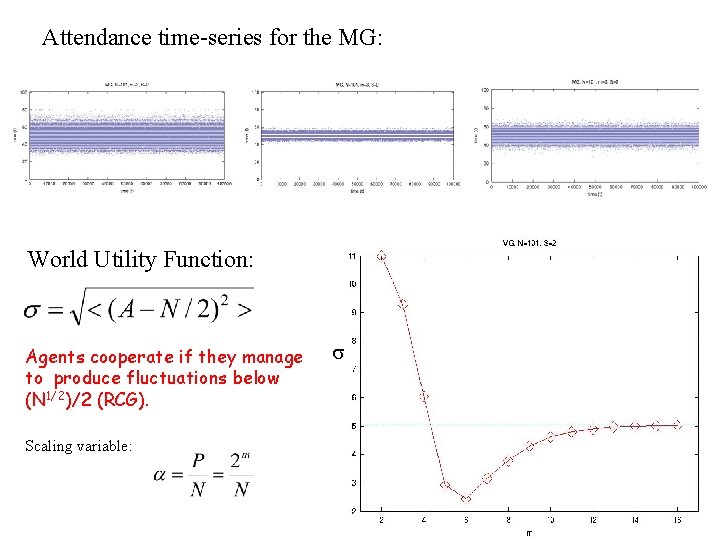
Attendance time-series for the MG: World Utility Function: Agents cooperate if they manage to produce fluctuations below (N 1/2)/2 (RCG). Scaling variable:

The El Farol bar game on a social network A B …

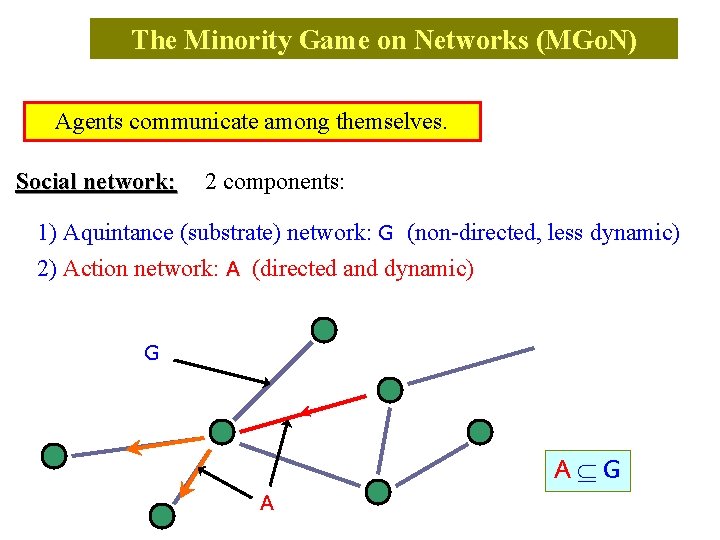
The Minority Game on Networks (MGo. N) Agents communicate among themselves. Social network: 2 components: 1) Aquintance (substrate) network: G (non-directed, less dynamic) 2) Action network: A (directed and dynamic) G A

Communication types (more bounded rationality): Majority rule (not rational) Minority rule (not rational) Critic’s rule: rule an agent listens to the OPINION/PREDICTION of all neighboring agents on G, scores them (self included) based on their past predictions, and ACTS on the best score. (more rational, uses reinforcement learning) (Links)(i) = (Scores)(i) = F (i)(j), j= 1, 2, . . , K. i (Prediction) (i) =

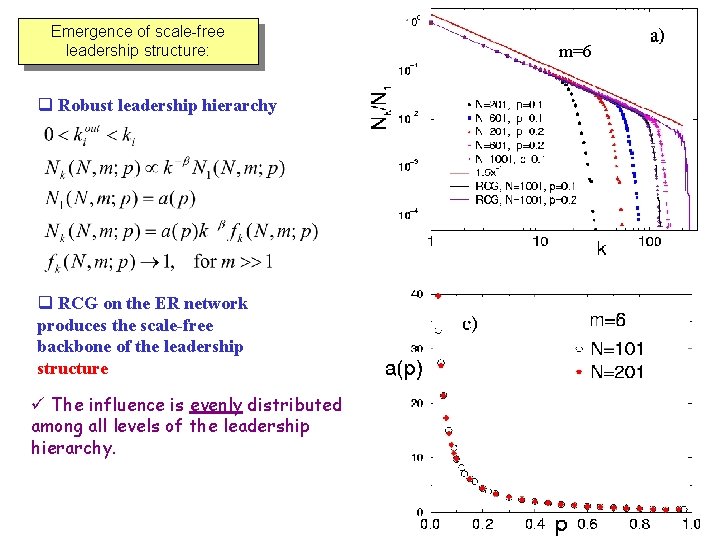
Emergence of scale-free leadership structure: q Robust leadership hierarchy q RCG on the ER network produces the scale-free backbone of the leadership structure ü The influence is evenly distributed among all levels of the leadership hierarchy. m=6

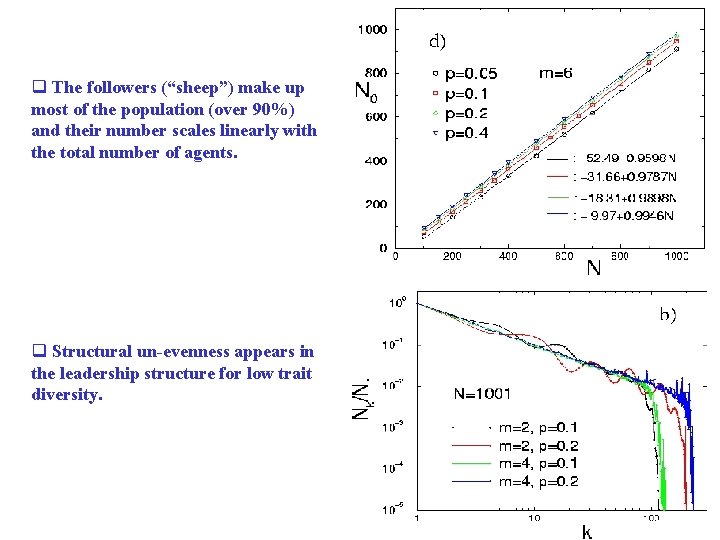
q The followers (“sheep”) make up most of the population (over 90%) and their number scales linearly with the total number of agents. q Structural un-evenness appears in the leadership structure for low trait diversity.

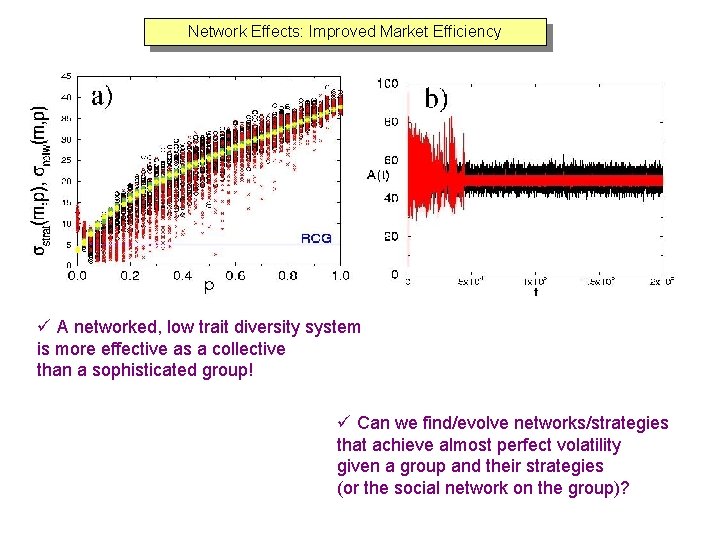
Network Effects: Improved Market Efficiency ü A networked, low trait diversity system is more effective as a collective than a sophisticated group! ü Can we find/evolve networks/strategies that achieve almost perfect volatility given a group and their strategies (or the social network on the group)?

Conclusions : • We defined Gradient Networks as directed sub-graphs formed by local gradients of a scalar distributed on a substrate graph G. • When the gradient direction is unique these Gradient Networks form forests. • Gradient Networks typically arise when there is a local extremizing dynamics at the node level (Agent-based Systems such as markets, routers, parallel computers, etc. . )). • Gradient Networks can be scale-free graphs even on substrate networks that are NOT scale-free networks (such as E-R graphs)!! • Gradient Networks can be highly dynamic, their evolution driven by the dynamics of the scalar field on G and they are not solely defined through the topological properties of G!! (such as in the case of preferential attachment). • G. N. -s give a natural explanation for why scale-free large networks might emerge if the edges have the same conductance and the flows are generated by gradients.