Fast Spectral Algorithms from SumofSquares Proofs Tensor Decomposition

Fast Spectral Algorithms from Sum-of-Squares Proofs: Tensor Decomposition and Planted Sparse Vectors Sam Hopkins Tselil Schramm Jonathan Shi David Steurer Cornell UC Berkeley Cornell

Competing Themes in Algorithms Polynomial time = Efficient algorithms BUT Stronger convex programs ↓ better (poly-time) algorithms ↓ (which aren’t really efficient) versus

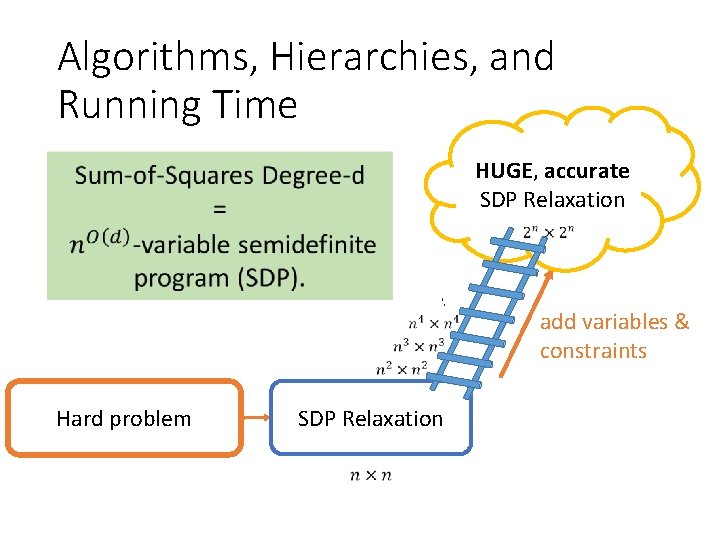
Algorithms, Hierarchies, and Running Time HUGE, accurate SDP Relaxation add variables & constraints Hard problem SDP Relaxation

Algorithms, Hierarchies, and Running Time Better approximation ratios, noise tolerance, than linear programs, semidefinite programs. New Algorithms for: • Scheduling [Levey-Rothvoss] • Independent sets in bounded-degree graphs [Bansal, Chlamtac] • Independent sets in hypergraphs [Chlamtac, Chlamtac-Singh] • Planted problems [Barak-Kelner-Steurer, Barak-Moitra, Hopkins • Shi-Steurer, Ge-Ma, Raghavendra-Rao-Schramm, Ma-Shi-Steurer] Unique games [Barak-Raghavendra-Steurer, Barak-Brandao. Harrow-Kelner-Steurer-Zhou]

Algorithms, Hierarchies, and Running Time

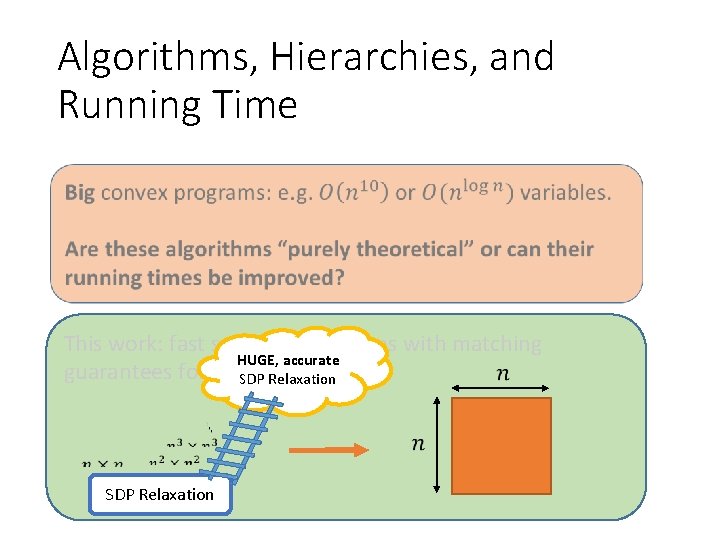
Algorithms, Hierarchies, and Running Time This work: fast spectral algorithms with matching guarantees for planted problems. Use eigenvectors of matrix polynomials

Algorithms, Hierarchies, and Running Time This work: fast spectral algorithms with matching HUGE, accurate guarantees for planted problems. SDP Relaxation

Results (1) Planted Sparse Vector (2) Random Tensor Decomposition (3) Tensor Principal Component Analysis

Results • So. S (previous champion) has to solve large SDP (much larger than input size)

Results (1) Planted Sparse Vector Match So. S guarantees, nearly-linear time (3) Tensor Principal Component Analysis Match So. S guarantees, linear time

Results (1) Planted Sparse Vector Match So. S guarantees, nearly-linear time (3) Tensor Principal Component Analysis Match So. S guarantees, linear time

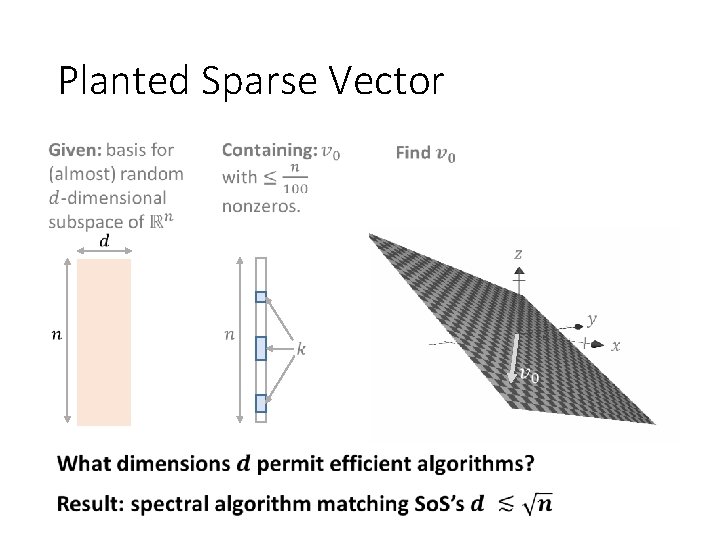
Planted Sparse Vector

Planted Sparse Vector

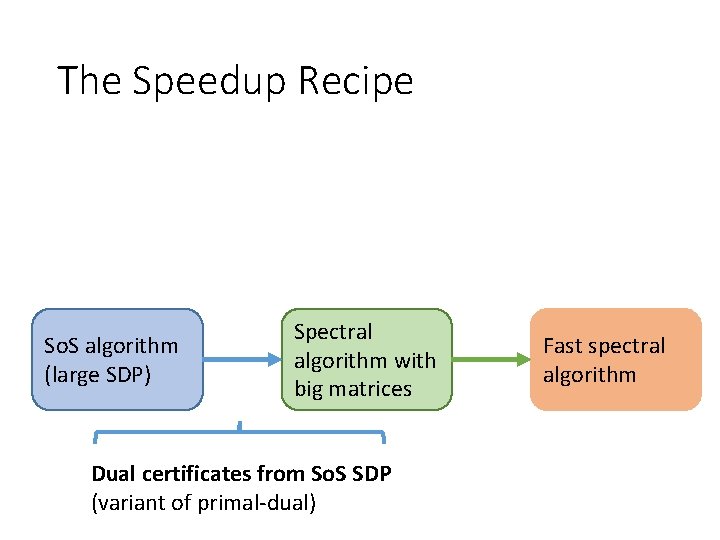
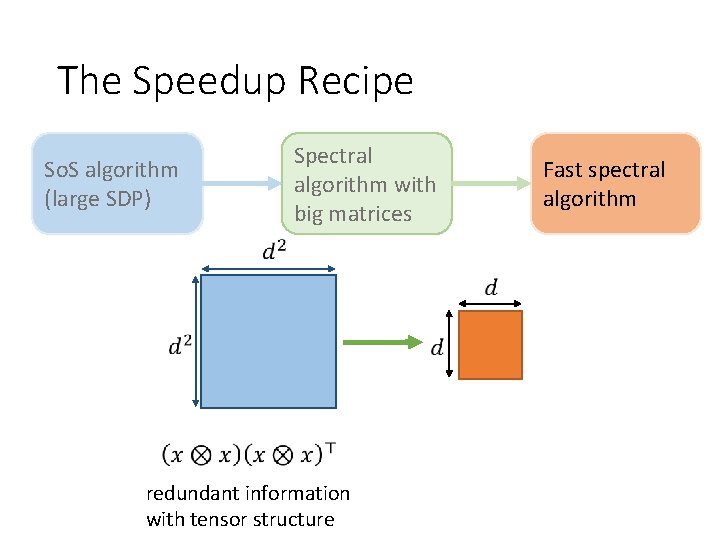
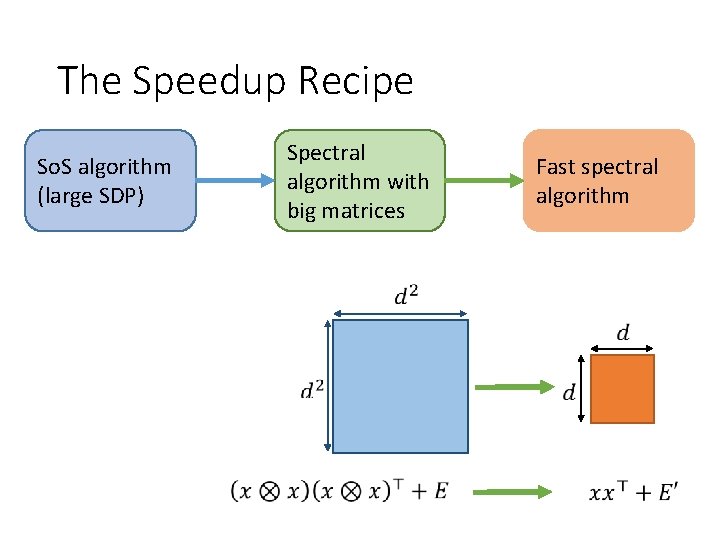
The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Dual certificates from So. S SDP (variant of primal-dual) Fast spectral algorithm

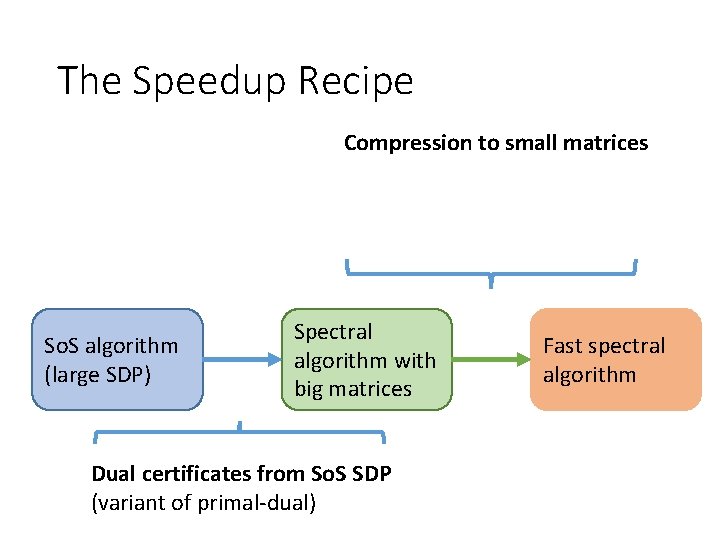
The Speedup Recipe Compression to small matrices So. S algorithm (large SDP) Spectral algorithm with big matrices Dual certificates from So. S SDP (variant of primal-dual) Fast spectral algorithm

The Speedup Recipe Compression to small matrices Different from — matrix multiplicative weights [Arora-Kale] — simpler spectral algorithms So. S algorithm (large SDP) Spectral algorithm with big matrices Dual certificates from So. S SDP (variant of primal-dual) Fast spectral algorithm

The Speedup Recipe Not local rounding [Guruswami-Sinop] So. S algorithm (large SDP) Compression to small matrices Different from — matrix multiplicative weights [Arora-Kale] — simpler spectral algorithms Spectral algorithm with big matrices Dual certificates from So. S SDP (variant of primal-dual) Fast spectral algorithm

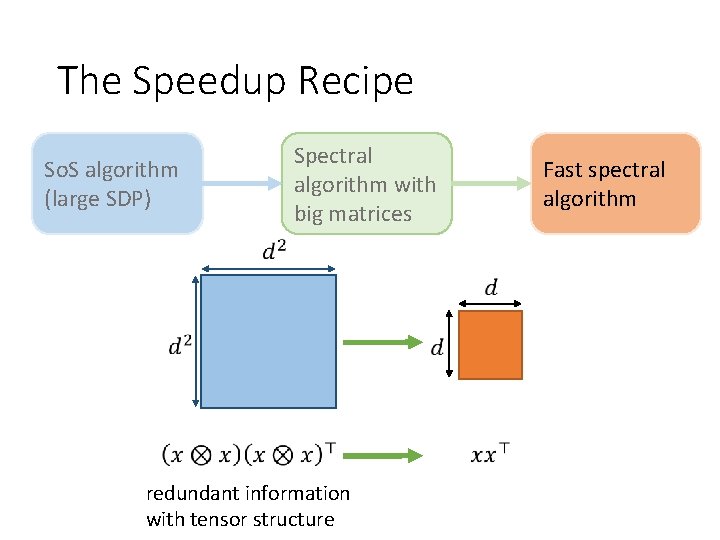
The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

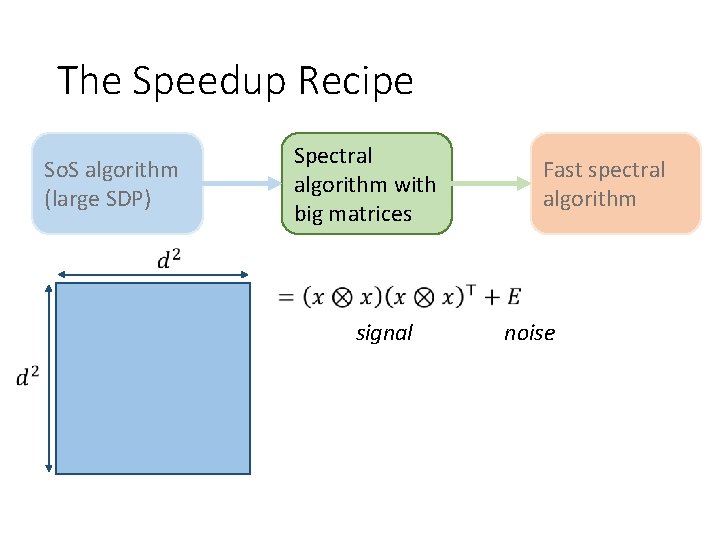
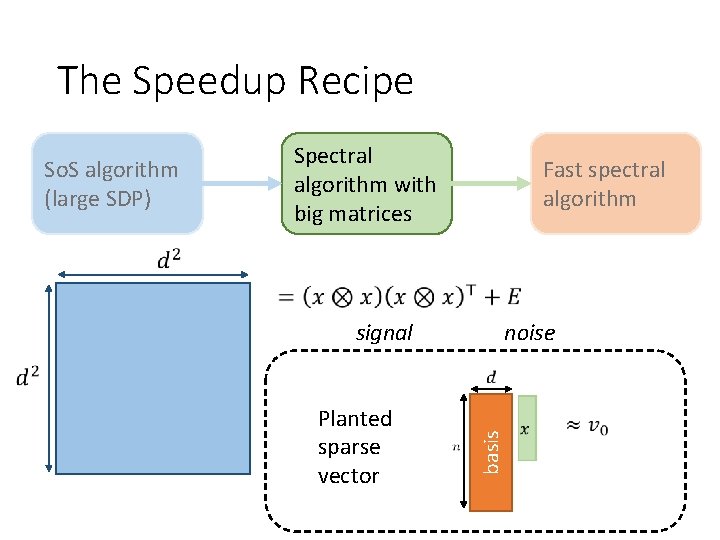
The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices signal Fast spectral algorithm noise

The Speedup Recipe Fast spectral algorithm signal Planted sparse vector noise basis So. S algorithm (large SDP) Spectral algorithm with big matrices

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

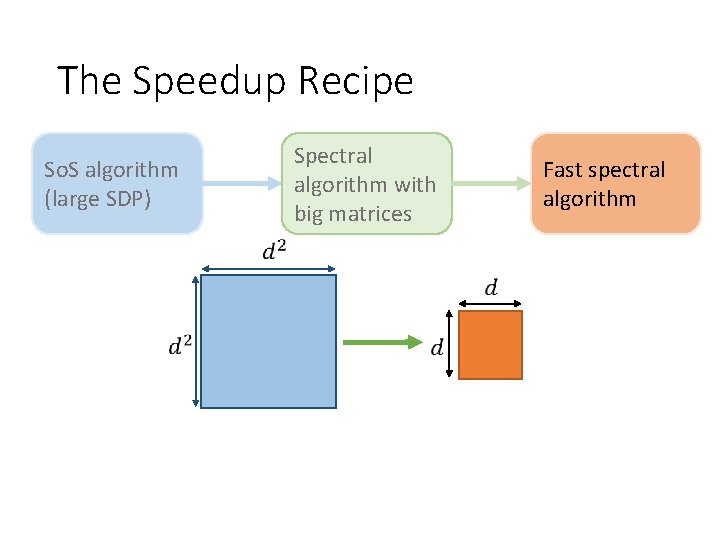
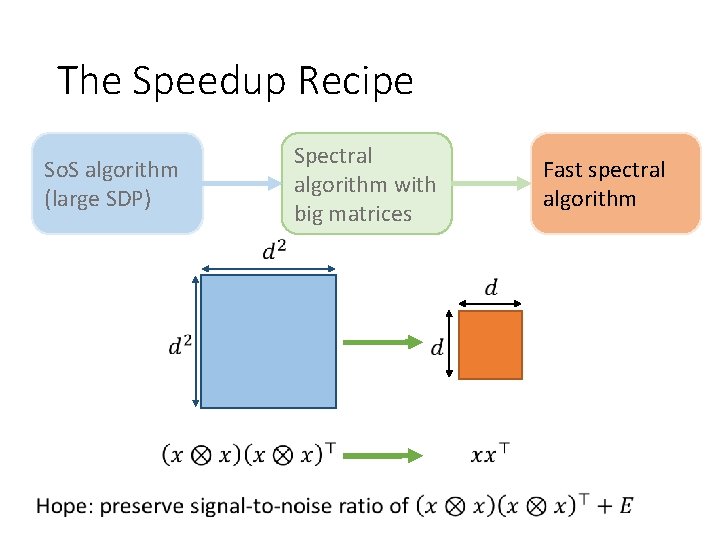
The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices redundant information with tensor structure Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices redundant information with tensor structure Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

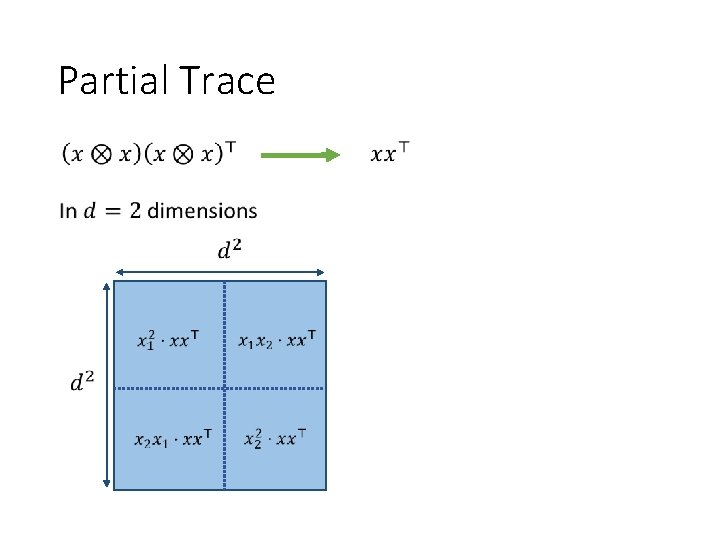
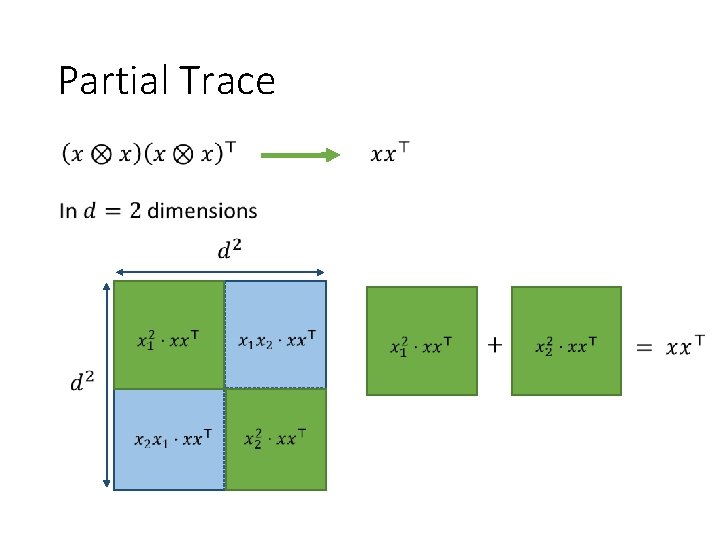
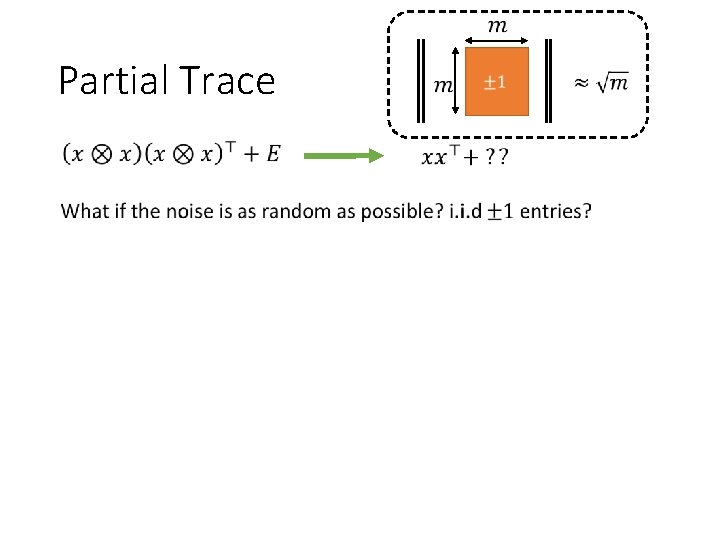
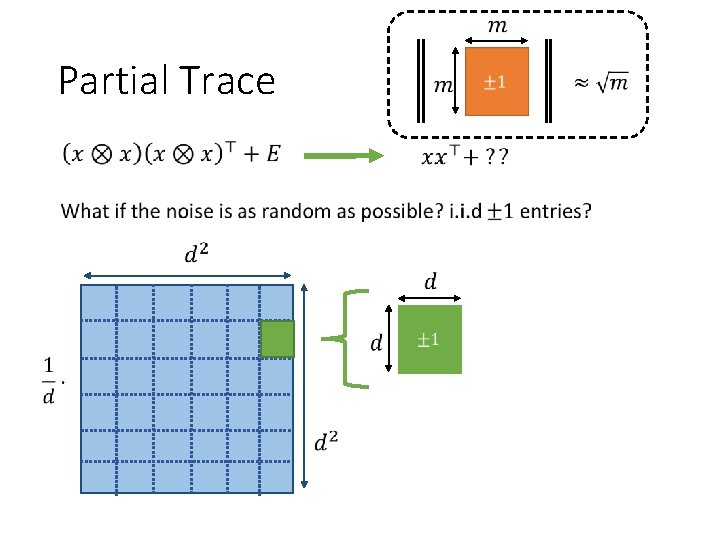
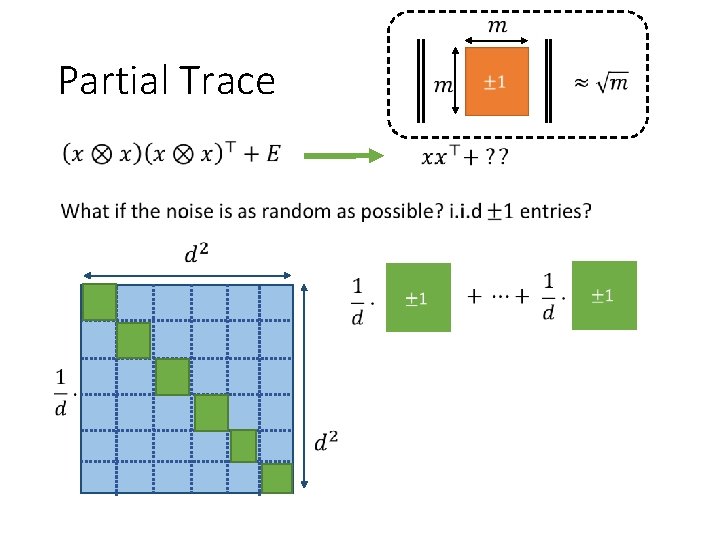
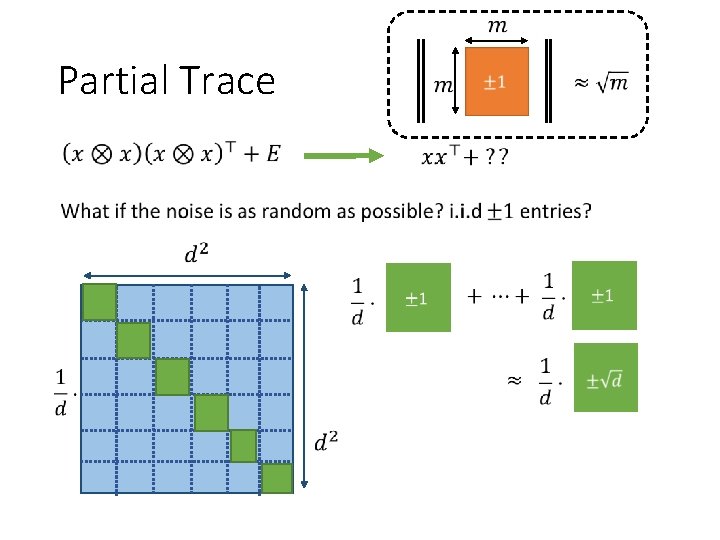
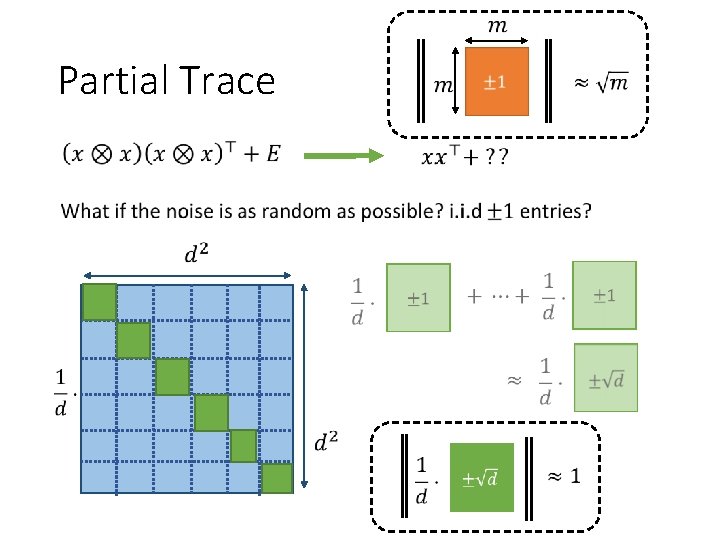
Partial Trace

Partial Trace

Partial Trace

Partial Trace

Partial Trace

Partial Trace

Partial Trace

Partial Trace

Partial Trace

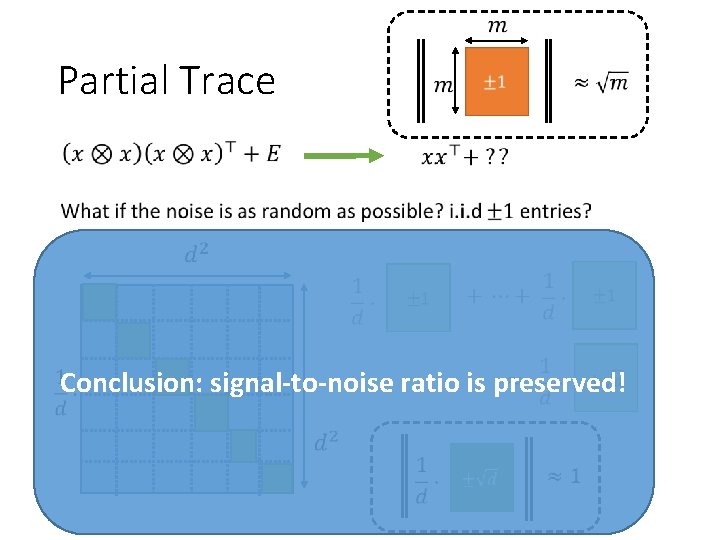
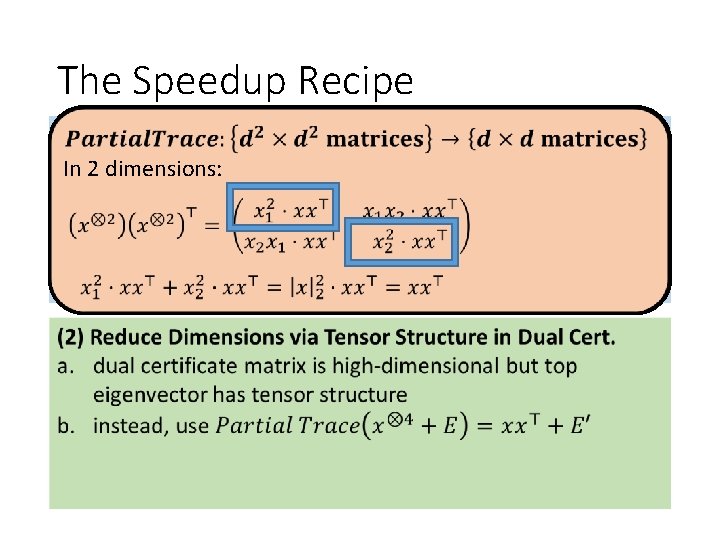
Partial Trace Conclusion: signal-to-noise ratio is preserved!

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

The Speedup Recipe So. S algorithm (large SDP) Spectral algorithm with big matrices Fast spectral algorithm

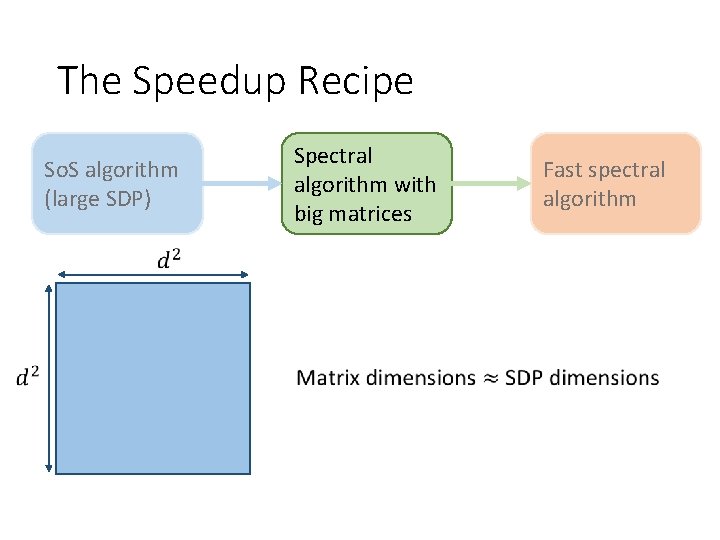
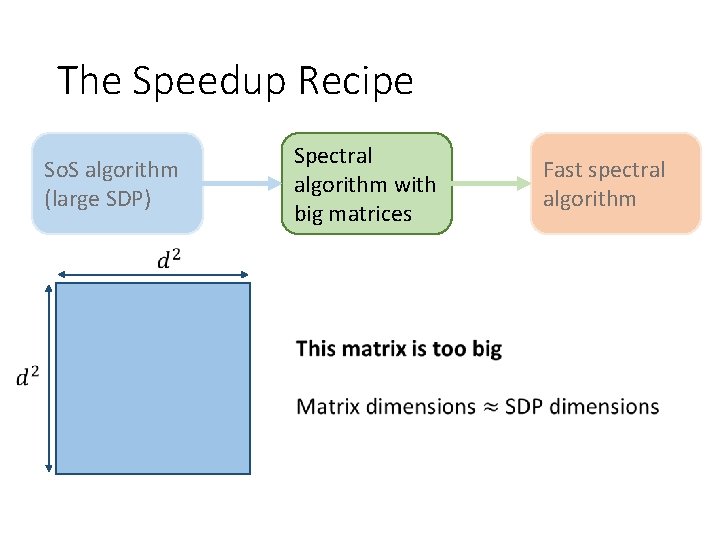
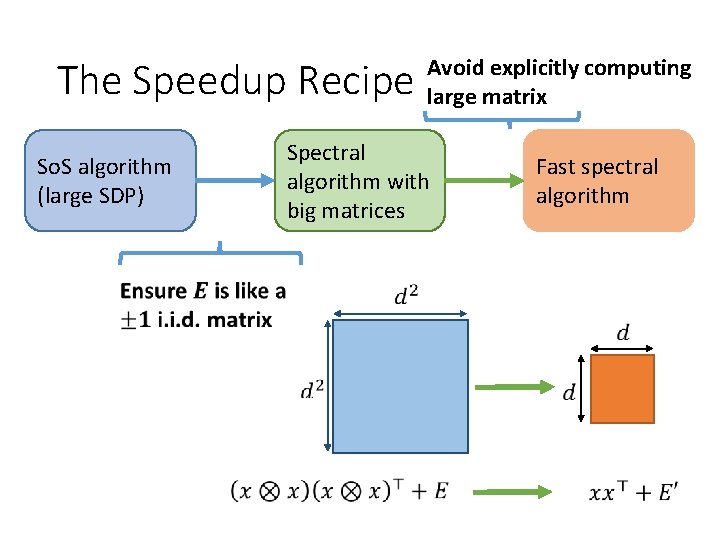
The Speedup Recipe So. S algorithm (large SDP) Avoid explicitly computing large matrix Spectral algorithm with big matrices Fast spectral algorithm

Resulting Algorithms are Simple and Spectral

Resulting Algorithms are Simple and Spectral

Resulting Algorithms are Simple and Spectral

basis Resulting Algorithms are Simple and Spectral

basis Resulting Algorithms are Simple and Spectral

Conclusions By exploiting tensor structure in dual certificates, randomness in inputs, impractical So. S algorithms can become practical spectral algorithms. Thanks For Coming!

The Resulting Algorithms are Simple and Spectral

The Resulting Algorithms are Simple and Spectral

The Resulting Algorithms are Simple and Spectral

Contrast to Previous Speedup Approaches (Matrix) Multiplicative Weights [Arora-Kale]: Cannot go faster than matrix-vector multiplication for matrices in the underlying SDP.

The Speedup Recipe (1) Understand Spectrum of So. S Dual Certificate (avoid SDP) (2) Reduce Dimensions via Tensor Structure in Dual Cert.

The Speedup Recipe • (2) Reduce Dimensions via Tensor Structure in Dual Cert.

The Speedup Recipe •

The Speedup Recipe (1) Understand Spectrum of So. S Dual Certificate In 2 dimensions: the result: a spectral algorithm using high-dimensional matrices.

The Speedup Recipe (1) Understand Spectrum of So. S Dual Certificate the result: a spectral algorithm using high-dimensional matrices.

The Speedup Recipe (1) Understand Spectrum of So. S Dual Certificate the result: a spectral algorithm using high-dimensional matrices.

The Speedup Recipe (1) Understand Spectrum of So. S Dual Certificate the result: a spectral algorithm using high-dimensional matrices.

Thanks For Coming!

Can We Use Previous Approaches to Speeding Up Relaxation-Based Algorithms?

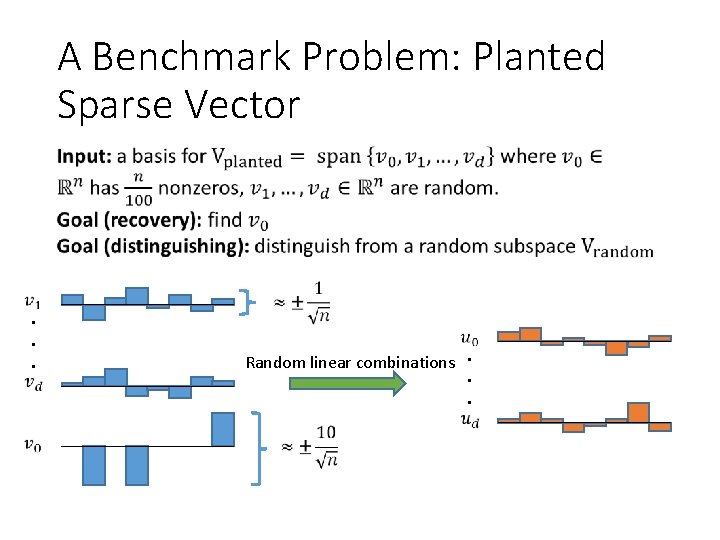
A Benchmark Problem: Planted Sparse Vector • . . . Random linear combinations. . .

A Benchmark Problem: Planted Sparse Vector

A Benchmark Problem: Planted Sparse Vector

A Benchmark Problem: Planted Sparse Vector Related to compressed sensing, dictionary learning, sparse pca, shortest codeword, small-set expansion

A Benchmark Problem: Planted Sparse Vector Simple problem where sum-of-squares (So. S) hierarchy beats LP, (small) SDPs, local search

Previous Work (recovery version) Authors [Spielman-Wang-Wright, Demanet-Hand] Subspace Dimension Technique Linear Programming

Previous Work (recovery version) Authors Subspace Dimension Technique [Spielman-Wang-Wright, Demanet-Hand] Linear Programming Folklore Semidefinite Programming

Previous Work (recovery version) Authors Subspace Dimension Technique [Spielman-Wang-Wright, Demanet-Hand] Linear Programming Folklore Semidefinite Programming [Qu-Sun-Wright] Alternating Minimization

Previous Work (recovery version) Authors Subspace Dimension Technique [Spielman-Wang-Wright, Demanet-Hand] Linear Programming Folklore Semidefinite Programming [Qu-Sun-Wright] Alternating Minimization [Barak-Brandao-Harrow-Kelner-Steurer-Zhou, Barak-Kelner-Steurer] So. S Hierarchy

Previous Work (recovery version) Authors [Spielman-Wang-Wright, Demanet-Hand] Subspace Dimension Technique Linear Programming All require polynomial loss in Folklore Semidefinite Programming sparsity or subspace dimension or both, compared with So. S. [Qu-Sun-Wright] Alternating Minimization [Barak-Brandao-Harrow-Kelner-Steurer-Zhou, Barak-Kelner-Steurer] So. S Hierarchy

Sum-of-Squares (and So. Sinspired) Algorithms Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer]

Sum-of-Squares (and So. Sinspired) Algorithms Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer]

Sum-of-Squares (and So. Sinspired) Algorithms Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit)

Sum-of-Squares (and So. Sinspired) Algorithms Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit) This work

Sum-of-Squares (and So. Sinspired) Algorithms Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit) This work Running-time barrier from dimension of convex program

Sum-of-Squares (and So. Sinspired) Algorithms Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit) This work Running-time barrier from dimension of convex program This work

[Barak et al]’s Distinguishing Algorithm Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit) This work

Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit) This work

Running Time Distinguishing Recovery [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] [Barak-Kelner. Steurer] [Barak-Brandao-Harrow-Kelner-Steurer. Zhou] (implicit) This work

(Breaking) The Dimension Barrier

(Breaking) The Dimension Barrier

The Recipe (1) So. S algorithms (often) come with dual certificate constructions. (2) Explicitly compute spectrum of dual certificate. (3) Compress to lower dimensions using randomness to avoid losing information.