Fast Sequence Alignment Methods Using CUDAenabled GPU Authors

Fast Sequence Alignment Methods Using CUDA-enabled GPU Authors: Yeim-Kuan Chang, De-Yu Chen Present: Pei-Hua Huang Date: 2014/06/04 Department of Computer Science and Information Engineering National Cheng Kung University, Taiwan R. O. C.

INTRODUCTION l l Sequence alignment is the first step in bioinformatics research that calculates the degree of similarity between two sequences A large of biological data is stored in the form of DNA, RNA and protein sequences, and made of their respective letters set shown below: • • • DNA : {A, C, G, T} RNA : {A, C, G, U} Protein : {A, R, N, D, C, Q, E, G, H, I, L, K, M, F, P, S, T, W, Y, V} Computer & Internet Architecture Lab CSIE, National Cheng Kung University 2

INTRODUCTION l only a selected set of operations is allowed at each aligning position: 1. match one letter with another, 2. mismatch one letter with another, 3. align one letter with a gap (denoted by "－") symbol for increasing similarity S 1 = A － G G C C T A － T G S 2 = A C G G C C T A A T C match gap Computer & Internet Architecture Lab CSIE, National Cheng Kung University mismatch 3

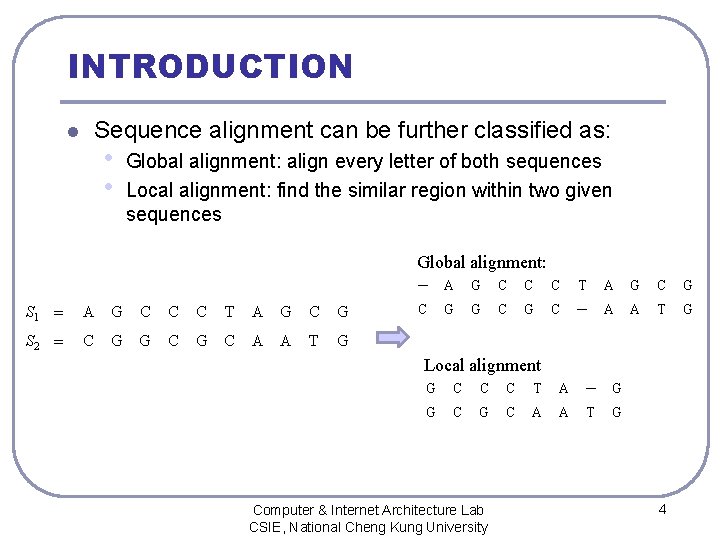
INTRODUCTION Sequence alignment can be further classified as: l • • Global alignment: align every letter of both sequences Local alignment: find the similar region within two given sequences Global alignment: S 1 = A G C C C T A G C G S 2 = C G G C A A T G － A G C C C T A G C G G C － A A T G Local alignment G C C C T A － G G C A A T G Computer & Internet Architecture Lab CSIE, National Cheng Kung University 4

Smith-Waterman algorithm l In order to quantify an alignment, SW algorithm uses a scoring mechanism which has three types of score as follows: • • • l Match score if S 1[i] = S 2[j]. Mismatch score if S 1[i] ≠ S 2[j] Gap penalty score if S 1[i] = ”－” or S 2[j] = ”－”, or both The match and mismatch scores obtained by looking up a substitution matrix in which each cell contains a score for the corresponding pair of based Computer & Internet Architecture Lab CSIE, National Cheng Kung University 5

Smith-Waterman algorithm l l Given two sequences S 1 and S 2 of length m and n Let H be a score matrix of size (m+1)(n+1). The recursive formula is defined as: where 1 ≤ i ≤ m, 1 ≤ j ≤ n, sbt(S 1[i], S 2[j]) gets the match or mismatch score, g is the score of gap penalty H[ i ][ 0 ] and H[ 0 ][ j ] for 0 ≤ i ≤ m and 0 ≤ j ≤ n are initialized as 0 Computer & Internet Architecture Lab CSIE, National Cheng Kung University 6

Smith-Waterman algorithm Computer & Internet Architecture Lab CSIE, National Cheng Kung University 7

Smith-Waterman algorithm j → 0 1 2 3 4 5 6 7 8 9 10 C C A C C G G C 0 ← 0 ↑ 0 ↑ 0 ↑ 0 ← 0 ↖ 9 ↖ 5 ↑ 1 ↑ 0 ↖ 0 ← 0 ↖ 5 ← 13 ↖ 9 ↖ 5 ↖ 1 ↖ 0 ← 0 ↖ 9 ← 10 ↖ 6 ↖ 2 ↖ 0 ← 0 ↖ 9 ↖ 6 ↖ 7 ↖ 3 ↖ 0 ← 6 ↖ 5 ← 9 ↖ 15 ↖ 12 ↖ 13 ↖ 0 ← 6 ↖ 3 ↖ 5 ↖ 15 ↖ 21 ↖ 18 ↖ 0 ← 6 ↖ 3 ↖ 11 ↖ 27 ↖ 0 ← 6 ↖ 3 ↖ 9 ↖ 17 ↖ 27 ↖ 0 ← 2 ← 15 ↖ 11 ↑ 7 ↑ 13 ↑ 23 ↑ 0 ↑ 0 ↑ 0 ↖ 0 ↖ 0 ↖ 4 ↖ 0 ↖ 0 ↖ 1 ↖ 0 ↖ 0 ↖ 9 ↑ 5 ↑ 1 ↑ 6 ↖ 14 ↑ 10 ↑ 6 ↑ 7 ↖ 23 ↑ 19 ↑ 15 ↑ 12 ↖ 25 ↖ 21 ↖ 19 ↖ 21 ↖ 26 ↖ 24 ↖ 21 ↖ 17 ↑ i↓ 0 1 2 G 3 C 4 A 5 G 6 G 7 G 8 T 9 T 10 A 11 G Computer & Internet Architecture Lab CSIE, National Cheng Kung University S 1 = C A G G G S 2 = C C G G G 8

Parallelism mechanisms 1. exploits the parallel characteristics of cells in the anti-diagonals, that is, each anti-diagonal cell can be computed independently of the others (i 2) (i 1) i (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (1, 7) (1, 8) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (2, 7) (2, 8) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (3, 7) (3, 8) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (4, 7) (4, 8) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (5, 7) (5, 8) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) (6, 7) (6, 8) (7, 1) (7, 2) (7, 3) (7, 4) (7, 5) (7, 6) (7, 7) (7, 8) Computer & Internet Architecture Lab CSIE, National Cheng Kung University 9

Parallelism mechanisms 2. The matrix is computed vector by vector in order parallel to the query sequence 1 2 3 4 5 6 7 (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (1, 7) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (2, 7) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (3, 7) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (4, 7) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (5, 7) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) (6, 7) (7, 1) (7, 2) (7, 3) (7, 4) (7, 5) (7, 6) (7, 7) (8, 1) (8, 2) (8, 3) (8, 4) (8, 5) (8, 6) (8, 7) 8 9 10 11 12 13 Computer & Internet Architecture Lab CSIE, National Cheng Kung University 14 10

Parallelism mechanisms 3. processe the vector in parallel to the query sequence and at the same time it processes the vector from the next column in anti-diagonal direction (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (1, 7) (1, 8) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (2, 7) (2, 8) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (3, 7) (3, 8) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (4, 7) (4, 8) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (5, 7) (5, 8) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) (6, 7) (6, 8) (7, 1) (7, 2) (7, 3) (7, 4) (7, 5) (7, 6) (7, 7) (7, 8) (8, 1) (8, 2) (8, 3) (8, 4) (8, 5) (8, 6) (8, 7) (8, 8) (9, 1) (9, 2) (9, 3) (9, 4) (9, 5) (9, 6) (9, 7) (9, 8) (10, 1) (10, 2) (10, 3) (10, 4) (10, 5) (10, 6) (10, 7) (10, 8) (11, 1) (11, 2) (11, 3) (11, 4) (11, 5) (11, 6) (11, 7) (11, 8) (12, 1) (12, 2) (12, 3) (12, 4) (12, 5) (12, 6) (12, 7) (12, 8) Computer & Internet Architecture Lab CSIE, National Cheng Kung University 11

Proposed method l Redefine the recursive formula of SW algorithm so that one row of the matrix can be calculated in parallel j → 0 i↓ 0 0 1 a 1 0 2 a 2 0 3 a 3 0 1 2 3 4 5 6 7 8 b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 0 0 0 0 Computer & Internet Architecture Lab CSIE, National Cheng Kung University 12

Proposed method l In order to compute the scores in parallel, we have the following new formula: Computer & Internet Architecture Lab CSIE, National Cheng Kung University 13

Proposed method Computer & Internet Architecture Lab CSIE, National Cheng Kung University 14

Proposed method expand to Computer & Internet Architecture Lab CSIE, National Cheng Kung University 15

Proposed method Next, the expanded formula is as follows. Computer & Internet Architecture Lab CSIE, National Cheng Kung University 16

Proposed method Next, the expanded formula is as follows. Computer & Internet Architecture Lab CSIE, National Cheng Kung University 17

Proposed method The formula (a) can be performed by the threads assigned to the cells in parallel. After the first step is finished, formulas (b) and (c) are then executed. Where 1≦i≦m, 1≦j≦n. Computer & Internet Architecture Lab CSIE, National Cheng Kung University 18

Optimization l use prefix max scan to speed up the computation of the formula (b) The prefix max scan is defined as: Input: array[a , . . . , a ]. Output: array[a , M(a , a ), . . , M(a , a )] The prefix max scan is performed in k steps where k = log 2(n). For step i = 0 to k – 1, the element array[j] will be compared with array[j– 2 i] for j = 2 i + 1 to n in parallel, and store the result in array[j] 1 2 1 n 1 2 1 3 Computer & Internet Architecture Lab CSIE, National Cheng Kung University 1 n 19

Optimization H’[1][1]+7 g H’[1][2]+6 g H’[1][3]+5 g H’[1][4]+4 g H’[1][5]+3 g H’[1][6]+2 g H’[1][7]+g H’[1][8] a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 Step 1 a 1 M(a 1, a 2) M(a 2, a 3) M(a 3, a 4) M(a 4, a 5) M(a 5, a 6) M(a 6, a 7) M(a 7, a 8) Step 2 a 1 M(a 1, a 2) M(a 1, a 3) M(a 1, a 4) M(a 2, a 5) M(a 3, a 6) M(a 4, a 7) M(a 5, a 8) Step 3 a 1 M(a 1, a 2) M(a 1, a 3) M(a 1, a 4) M(a 1, a 5) M(a 1, a 6) M(a 1, a 7) M(a 1, a 8) -7 g -6 g -5 g -4 g -3 g -2 g -g -0 H’[1][1] Computer & Internet Architecture Lab CSIE, National Cheng Kung University 20

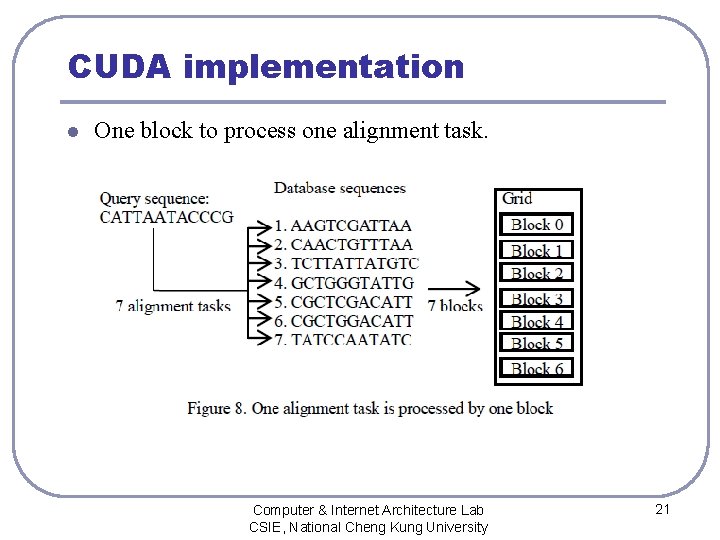
CUDA implementation l One block to process one alignment task. Computer & Internet Architecture Lab CSIE, National Cheng Kung University 21

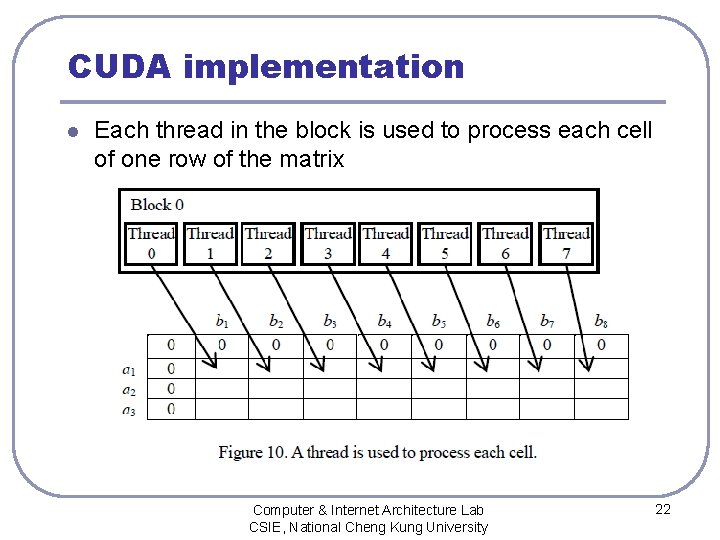
CUDA implementation l Each thread in the block is used to process each cell of one row of the matrix Computer & Internet Architecture Lab CSIE, National Cheng Kung University 22

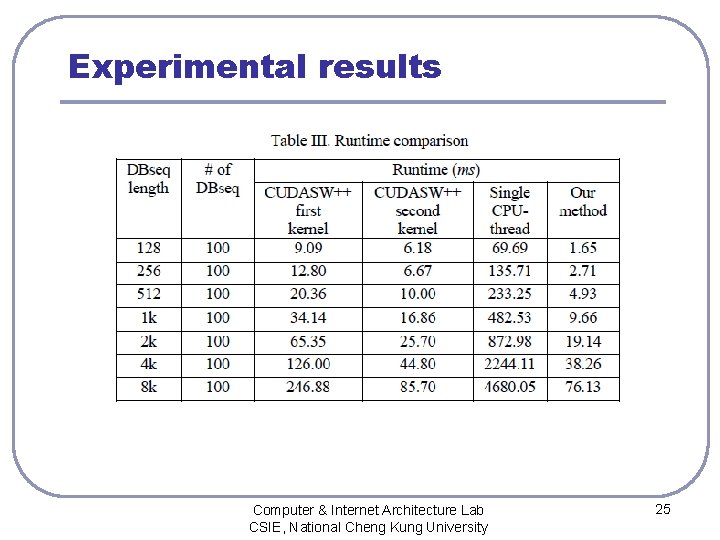
Experimental results l execute on NVIDIA C 1060 graphics card, with 30 MPs comprising 240 SPs and 4 GB RAM, installed in a PC with an Intel Core 2 6420 2. 13 GHz processor running the Ubuntu OS Computer & Internet Architecture Lab CSIE, National Cheng Kung University 23

Experimental results l l five databases are produced by Seq-Gen [16]. Each database includes 100 sequences of equal length, ranging from 128 to 8192 the substitution matrix BLOSUM 62 is used with gap penalty －4 Computer & Internet Architecture Lab CSIE, National Cheng Kung University 24

Experimental results Computer & Internet Architecture Lab CSIE, National Cheng Kung University 25

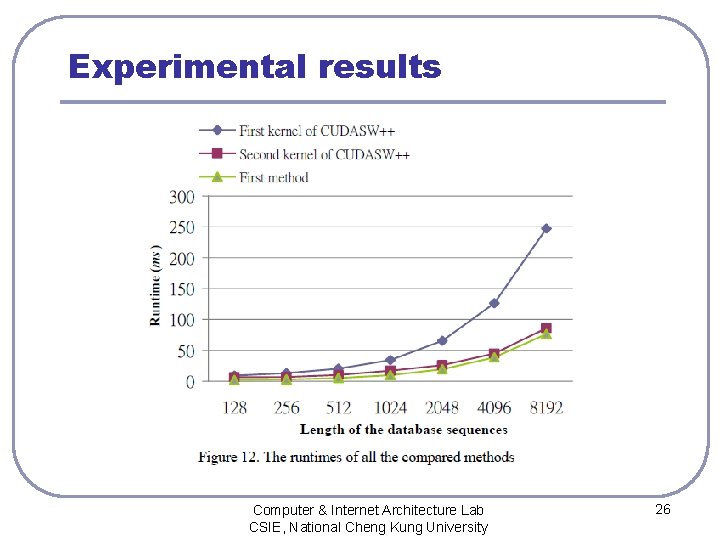
Experimental results Computer & Internet Architecture Lab CSIE, National Cheng Kung University 26