Fast Polynomial Factorization and Modular Composition Chris Umans

Fast Polynomial Factorization and Modular Composition Chris Umans Caltech joint work with Kiran Kedlaya (MIT) [Umans STOC 08] + [Kedlaya-Umans FOCS 08]

Introduction • A basic problem: given: degree n polynomial A(X) output: factorization into irreducible polynomials Example: given: A(X) = x 3 – 1 output: (x 2 + x + 1)(x – 1) Nov. 18, 2009 2

Introduction • factoring a degree n polynomial A(X) with coefficients in Fq is easy • Why? can easily compute i q (X – X) mod A(X) (contains all potential factors of degree dividing i; use GCD, and i = 1, 2, 3…, n) Nov. 18, 2009 3

Introduction • polynomial-time factoring in Fq[X] [Berlekamp, Cantor-Zassenhaus]: – make A(X) square-free – distinct degree factorization: A(X) = A 1(X)A 2(X). . . Ai(X)…An(X) – equal-degree factorization: Ai(X) = g 1(X)g 2(X)…gk(X) Nov. 18, 2009 product of degree i polynomials irreducible factors 4

Bottleneck in algorithms • how to compute this polynomial quickly: i q deg(A) = n; i ≤ n (X – X) mod A(X) Nov. 18, 2009 5

Bottleneck in algorithms • how to compute this polynomial quickly: i q deg(A) = n; i ≤ n X mod A(X) – repeated squaring: log(qi) = i log q operations “operations” = modular addition, multiplication, composition of degree n polynomials Nov. 18, 2009 6

Bottleneck in algorithms • how to compute this polynomial quickly: i q deg(A) = n; i ≤ n X mod A(X) – repeated squaring: log(qi) = i log q operations – modular composition: log q + log i operations von zur Gathen + Shoup 1992 • compute Xq mod A(X) using repeated squaring 2 • compose it with itself (Xq)q = Xq mod A(X) 2 q 2 4 q q • compose it with itself again (X ) = X “operations” = modular addition, multiplication, composition of degree n polynomials Nov. 18, 2009 7

Operations on polynomials degree n polynomials f(X), g(X), A(X) Operation: Time: • f(X) + g(X) mod A(X) O’(n) • f(X)g(X) mod A(X) O’(n) • f( 0), …, f( n) O’(n) • find f(X): f( 0)= 0, …, f( n) = n O’(n) • f(g(X)) mod A(X) O’(n 1. 667) Nov. 18, 2009 8

Modular composition given deg. n polynomials f(X), g(X), A(X) compute f(g(X)) mod A(X) • trivial in time O’(n 2) • best known [Brent-Kung 1978; Huang-Pan 1997] O’(n 1. 667) (= O(n 1. 5 + n 2/2) ) – idea: reduce problem to matrix multiplication This work: O’(n) Nov. 18, 2009 9

Outline • reduce to “multivariate multipoint evaluation” • new algorithm via multimodular reduction ) data structure for polynomial evaluation ) faster algorithms for polynomial factorization and other problems Nov. 18, 2009 10

The reduction given deg. n=2 m polynomials f(X), g(X), A(X) compute f(g(X)) mod A(X) • convert f(X) to multilinear: f(X 0, X 1, …, Xlog n-1) f(X) = f(X, X 2, X 4, X 8, …, Xn/2) i 2 • compute g (X) mod A(X) (call this gi(X)) for i = 0, 1, 2, …, log n -1 • note: f(g(X)) ´ f(g 0(X), …, glog n-1(X)) mod A(X) Nov. 18, 2009 11

The reduction given deg. n=2 m polynomials f(X), g(X), A(X) compute f(g(X)) mod A(X) • f(X) = f(X, X 2, X 4, X 8, …, Xn/2) degree n¢log n • f(g(X)) ´ f(g 0(X), …, glog n-1(X)) mod A(X) • idea: evaluate at n¢log n points; – evaluate each gi at n¢log n points – evaluate f at these n¢log n points in (Fq)log n then interpolate; reduce modulo A(X) Nov. 18, 2009 12

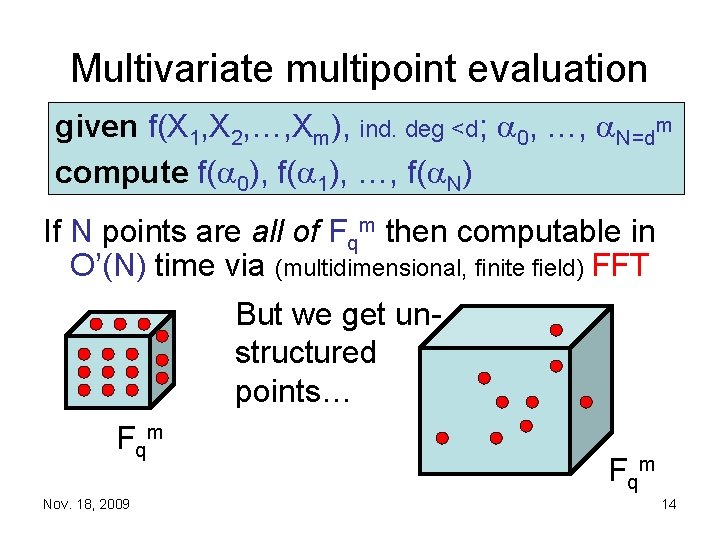
Multipoint evaluation • Recall univariate case: – given degree n polynomial f(X) 2 Fq[X] and points 0, 1, …, n – can compute f( 0), …, f( n) in time O’(n) • Multivariate case harder: – given f(X 1, X 2, …, Xm) 2 Fq[X 1, X 2, …, Xm] with individual degrees · d, and 0, 1, …, N=dm m – can compute f( 0), …, f( N) in time O’(N ) where 1. 3335 < m < 1. 667 [Nüsken-Ziegler 2004] Nov. 18, 2009 13

Multivariate multipoint evaluation given f(X 1, X 2, …, Xm), ind. deg <d; 0, …, N=dm compute f( 0), f( 1), …, f( N) If N points are all of Fqm then computable in O’(N) time via (multidimensional, finite field) FFT But we get unstructured points… F qm Nov. 18, 2009 F qm 14

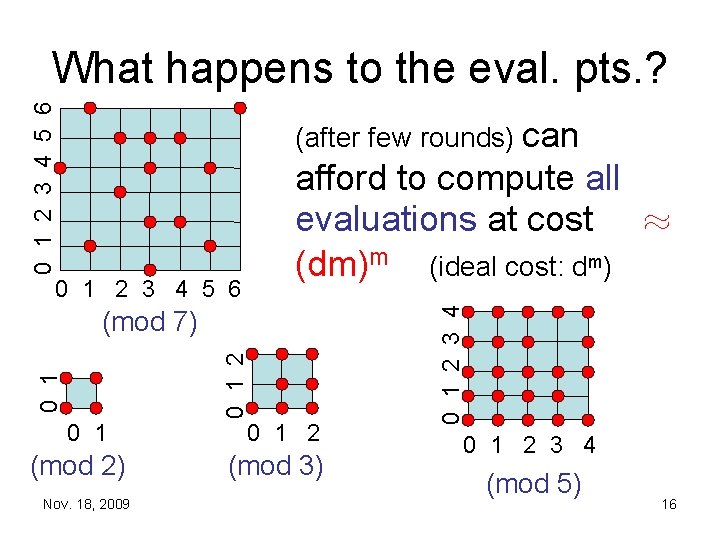
Multivariate multipoint evaluation • Assume working over Fp • Lift coefficients of f and the coordinates of each ®i to {0, 1, 2, …, p-1} µ Z • In integers, f(®i) · dmpdm = M • Solve problem mod primes p 1, p 2, …, pk with p 1 p 2…pk ¸ M (so pj · O(log M)) • reconstruct via Chinese Remainder Thm. • repeat; magnitude of the pj ! ¼ dm Nov. 18, 2009 15

0 1 2 3 4 5 6 What happens to the eval. pts. ? (after few rounds) can 0 1 2 3 4 5 6 0 1 2 (mod 7) 0 1 (mod 2) Nov. 18, 2009 0 1 2 (mod 3) 0 1 2 3 4 afford to compute all evaluations at cost ¼ (dm)m (ideal cost: dm) 0 1 2 3 4 (mod 5) 16

Multivariate multipoint evaluation given f(X 1, X 2, …, Xm), ind. deg <d; 0, …, N compute f( 0), f( 1), …, f( N) Theorem: for every const. ± > 0, can solve above problem in time (dm + N)1+± log 1+o(1)q provided m · do(1). Nov. 18, 2009 17

Data structure for poly. eval. Observation: reduced f’s and tables of evaluations over entire domains don’t depend on the set of evaluation points Theorem: given degree n poly f(X) over Fq, can produce a data structure in nearlylinear time that answers evaluation queries ® 2 Fq in time polylog(n)¢log 1+o(1)q. Nov. 18, 2009 18

Algorithmic improvements • modular composition in nearly-linear time (as well as its “transpose” problem) ) faster algorithms for – polynomial factorization: O’(n 1. 5 + nlog q)¢log q (best previous O’(n 2 + n log q)¢log q or O’(n 1. 815 log q)¢log q ) von zur Gathen + Shoup ‘ 92 Kaltofen + Shoup ‘ 98 – irreducibility testing: O’(n log q)¢log q – finding minimal polynomials: O’(n log q) Nov. 18, 2009 (improved exponents in all cases) 19

Open problems • Find an O’(n) algebraic algorithm for modular composition/multivariate multipoint evaluation in any characteristic • Find a fast algorithm for multivariate multipoint evaluation when m > do(1) • Find a nearly-linear time algorithm for polynomial factorization Nov. 18, 2009 20