Fast Polar Fourier Transform Michael Elad Scientific Computing

Fast Polar Fourier Transform Michael Elad* Scientific Computing and Computational Mathematics Stanford University Fo. CM Conference, August 2002 Image and Signal Processing Workshop IMA - Minneapolis * Joint work with Dave Donoho (Stanford-Statistics), Amir Averbuch (TAU-CS-Israel), and Ronald Coifman (Yale-Math) - 1 -

Collaborators Dave Donoho Amir Averbuch Statistics Department Stanford CS Department Tel -Aviv University Ronald Coifman Math. Department Yale - 2 -

Fast Polar Fourier Transform q FFT is one of top 10 algorithms of 20 th century. q We'll extend utility of FFT algorithms to new class of settings in image processing. q Create a tool which is: § Free of emotional involvement, & § Freely available over the internet. q Current Stage: § We have the tool, and its analysis, § Have not demonstrated applications yet. - 3 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art Background & Motivation 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis New Approach and its Results 8. Conclusions - 4 -

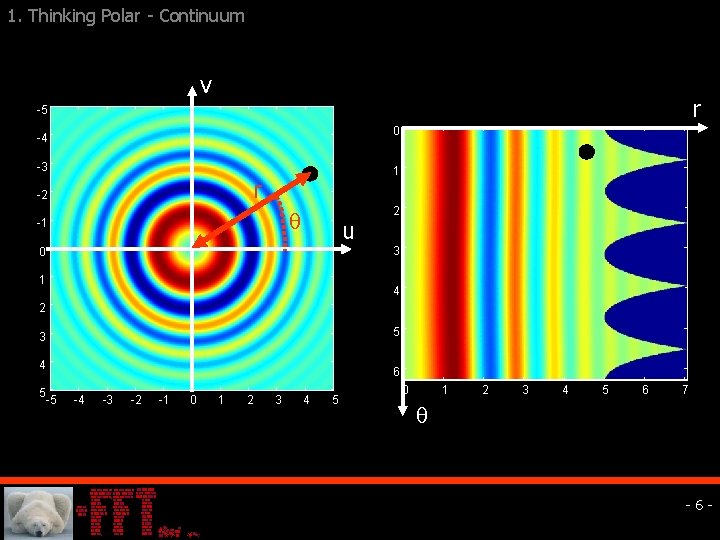
1. Thinking Polar - Continuum q For today f(x, y) function of (x, y) 2 q Continuous Fourier Transform q Polar coordinates: u=r·cos( ) , v=r·sin( ) q Important Processes easy to continuum polar domain. - 5 -

1. Thinking Polar - Continuum v r -5 0 -4 -3 1 r -2 -1 u 2 3 0 1 4 2 5 3 4 5 6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 - 6 -

1. Thinking Polar - Continuum Natural Operations: 1. Rotation Using the polar coordinates, rotation is simply a shift in the angular variable. q Q 0 – planar rotation by 0 degrees q Rotation q In polar coordinates – shift in angular variable - 7 -

1. Thinking Polar - Continuum Natural Operations: 2. Scaling Using the polar coordinates, 2 D scaling is simply a 1 D scaling in the radial variable. q S – planar scaling by a factor q Scaling q In polar coordinates – 1 D scale in radial variable q Log-Polar – shift in the radial variable. - 8 -

1. Thinking Polar - Continuum Natural Operations: 3. Registration Using the polar coordinates, rotation+shift registration simply amounts to correlations. q f(x, y) and g(x, y): q Goal: recover . q Angular cross-correlation between – Estimate 0. q Rotation & cross-correlation on regular Fourier transform gives the shift. - 9 -

1. Thinking Polar - Continuum Natural Operations: 4. Tomography Using the polar coordinates, we obtain a method to obtain the Inverse Radon Transform. q Radon Transform: q Goal: Given Rf(t, ), recover f. q Projection-Slice-Theorem: . q Reconstruction: . - 10 -

1. Thinking Polar - Continuum More Natural Operations q New orthonormal bases: § Ridgelets, § Curvelets, § Fourier Integral operations, § Ridgelet packets. q Analysis of textures. r q Analysis of singularities. q More … - 11 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 12 -

2. Thinking Polar - Discrete q Certain procedures very important to digitize § Rotation, § Scaling, § Registration, § Tomography, and § … q These look so easy in continuous theory – Can’t we use it in the discrete domain? q Why not Polar-FFT? - 13 -

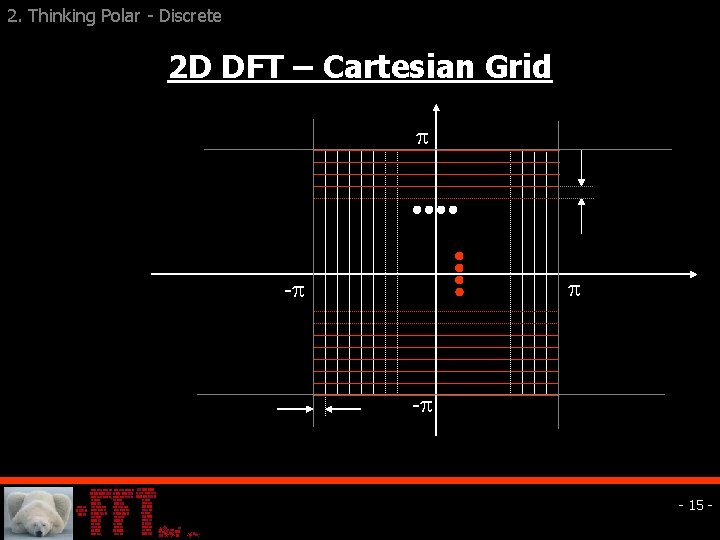
2. Thinking Polar - Discrete The FFT Miracles q 1 D Discrete Fourier Transform § Uniformly sampled in time and frequency – FFT. § Complexity – O(5 Nlog 2 N) instead of O(N 2). q 2 D Discrete Fourier Transform § Cartesian grid in space and frequency – Separability § Only 1 D-FFT operations. § Smart memory management. - 14 -

2. Thinking Polar - Discrete 2 D DFT – Cartesian Grid - - - 15 -

2 D FFT Complexity q Complexity: O(10 N 2 log 2 N) instead of O(N 4). q Important Feature: All operations are 1 D – leading to efficient cache usage Cartesian N-by-N Data 5 N 2 log. N 1 D FFT to columns 5 N 2 log. N 1 D FFT to rows Cartesian 2 D-FFT 10 N 2 log. N - 16 -

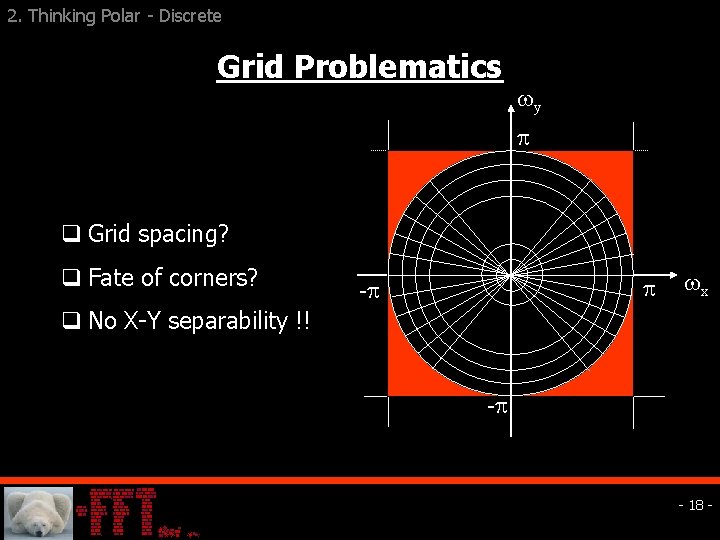
2. Thinking Polar - Discrete Polar Coordinates? y Choice of grid? Resulting with NS rays with NSr elements on each: For S =Sr=1, we have N 2 grid points. - x - - 17 -

2. Thinking Polar - Discrete Grid Problematics y q Grid spacing? q Fate of corners? - x q No X-Y separability !! - - 18 -

2. Thinking Polar - Discrete Polar FFT - Current Status q Current widespread belief - There cannot be a fast method for DFT on the polar grid. See e. g. The DFT: an owner’s manual, Briggs and Henson, SIAM, 1995, p. 284. q Consequence of Non-existence: § Continuous Fourier – vague inspiration only. § Fourier in implementations widely deprecated. § Fragmentation: each field special algorithm. - 19 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 20 -

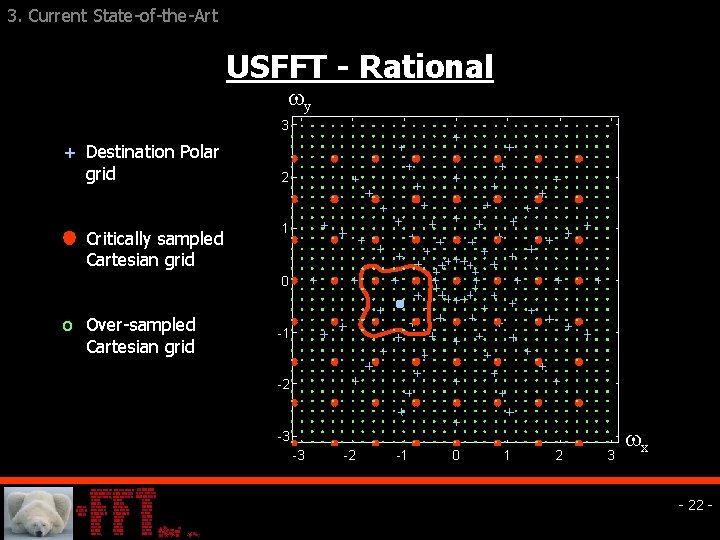
3. Current State-Of-The-Art q Assessing T: Unequally-spaced FFT (USFFT) § Data in Cartesian set. § Approximate transform in non-Cartesian set. § Oriented to 1 D – not 2 D and definitely not Polar. q Assessing T †: For Tomography § Data in Polar coordinates in frequency. § Approximate inverse transform to Cartesian grid. § Inspired by the projection-slice-theorem. - 21 -

3. Current State-of-the-Art USFFT - Rational y 3 + Destination Polar grid O Critically sampled Cartesian grid 2 1 0 o Over-sampled Cartesian grid -1 -2 -3 -3 -2 -1 0 1 2 3 x - 22 -

3. Current State-of-the-Art USFFT - Detailed q Over-sample Cartesian grid. q Rapidly evaluate FT: § Values F. § Possibly - partial derivatives. q Associate Cartesian neighbors to each polar grid point. q Approximate interpolation. - 23 -

3. Current State-of-the-Art Our Reading of Literature q Boyd (1992) – Over-sampling and interpolation by Euler sum or Langrangian interpolation. q Dutt-Rokhlin (1993, 1995) - Over-sampling and interpolation by the Fast-Multipole method. q Anderson-Dahleh (1996) – Over-sampling and obtaining the partial derivatives, and then interpolating by Taylor series. q Ware (1998) – Survey on USFFT methods. - 24 -

3. Current State-of-the-Art USFFT Problematics q Several involved parameters: § Over-sampling factor, § Method of interpolation, and § Order of interpolation. q Good accuracy calls for extensive over-sampling. q Correspondence overhead: spoils vectorizability of algorithm - causes high cache misses. q Emotionally involved. - 25 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 26 -

4. Our Approach - General We propose a Fast Polar Fourier Transform with the following features: § Low complexity – O(Const·N 2 log 2 N) § Vectorizability – 1 D operations only § Non-Expansiveness – Factor 2 (or 4) only § Stability – via Regularization § Accuracy – 2 orders of magnitude over USFFT methods - 27 -

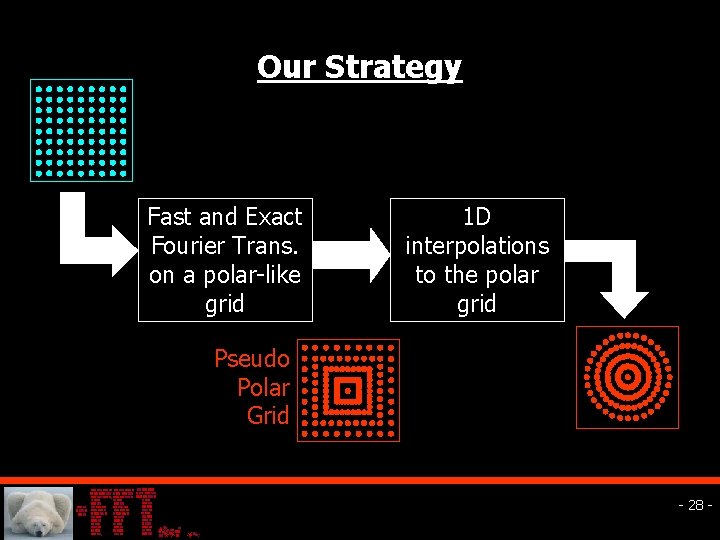
Our Strategy Fast and Exact Fourier Trans. on a polar-like grid 1 D interpolations to the polar grid Pseudo Polar Grid - 28 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 29 -

5. The Pseudo-Polar FFT q Developed by Averbuch, Coifman, Donoho, Israeli, and Waldén (1998). q Basic idea: A “Polar-Like” grid that enables § EXACT Fourier transform, § FAST computation, § 1 D operations only. q Applications: Tomography, image processing, Ridgelets, and more. - 30 -

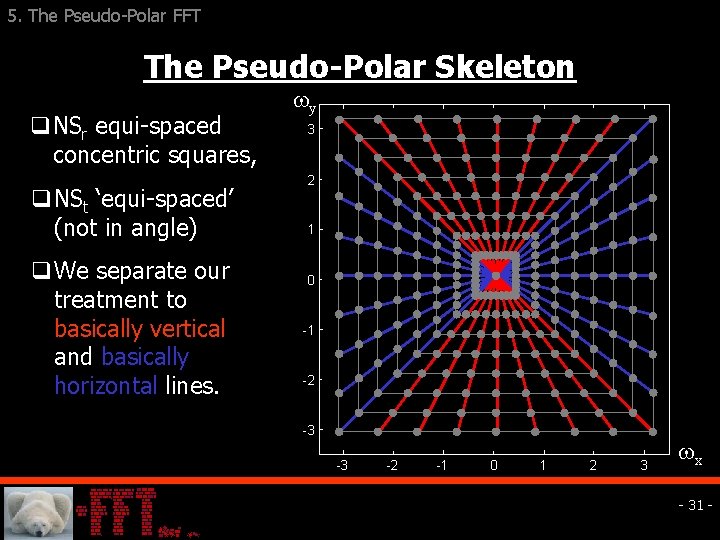
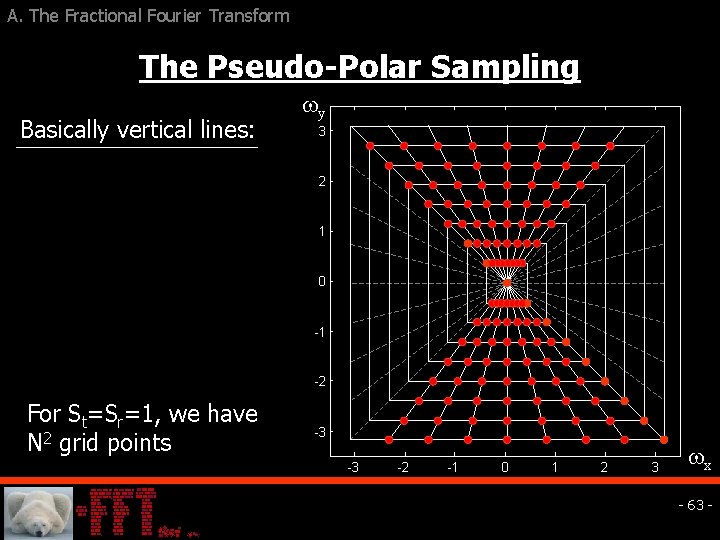
5. The Pseudo-Polar FFT The Pseudo-Polar Skeleton q NSr equi-spaced concentric squares, q NSt ‘equi-spaced’ (not in angle) q We separate our treatment to basically vertical and basically horizontal lines. y 3 2 1 0 -1 -2 -3 -3 -2 -1 0 1 2 3 x - 31 -

5. The Pseudo-Polar FFT Fast Fourier Transform q The destination samples are uniformly sampled vertically, q Per each row, destination samples are uniformly sampled horizontally, y 3 2 1 0 -1 q Fractional Fourier Transform is the answer -2 (Chirp-Z), with complexity: O(20 Nlog 2 N). -3 [Why? ] -3 -2 -1 0 1 2 3 x - 32 -

5. The Pseudo-Polar FFT PP-FFT versus 2 D-FFT Cartesian N-by-N Data PP-FFT 5 N 2 log. N 1 D FFT to columns 20 N 2 log. N 1 D FRFFT to rows PP-FFT 25 N 2 log. N vertical 2 D-FFT 5 N 2 log. N 1 D FFT to columns 5 N 2 log. N 1 D FFT to rows Cartesian 2 D-FFT 10 N 2 log. N - 33 -

5. The Pseudo-Polar FFT The PP-FFT - Properties q Exact in exact arithmetic. q No parameters involved !! q Complexity - O(50·N 2 log 2 N) versus O(N 4). q 1 D operations only. q For the chosen grid (Sr=St=2) - 5. - 34 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 35 -

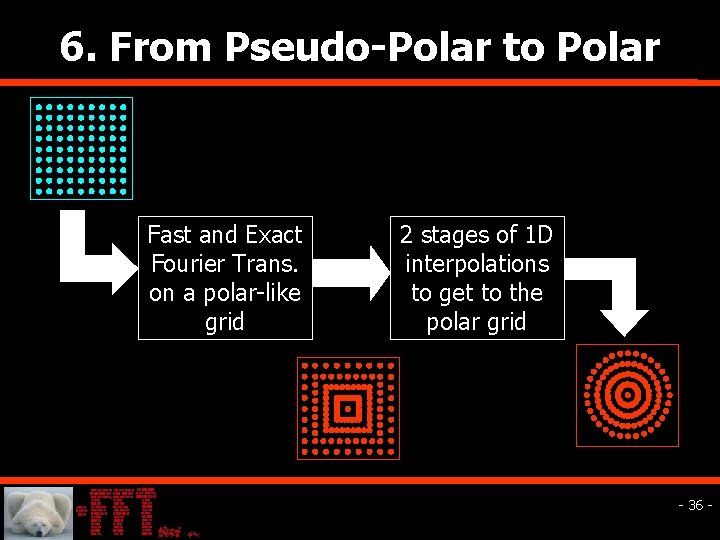
6. From Pseudo-Polar to Polar Fast and Exact Fourier Trans. on a polar-like grid 2 stages of 1 D interpolations to get to the polar grid - 36 -

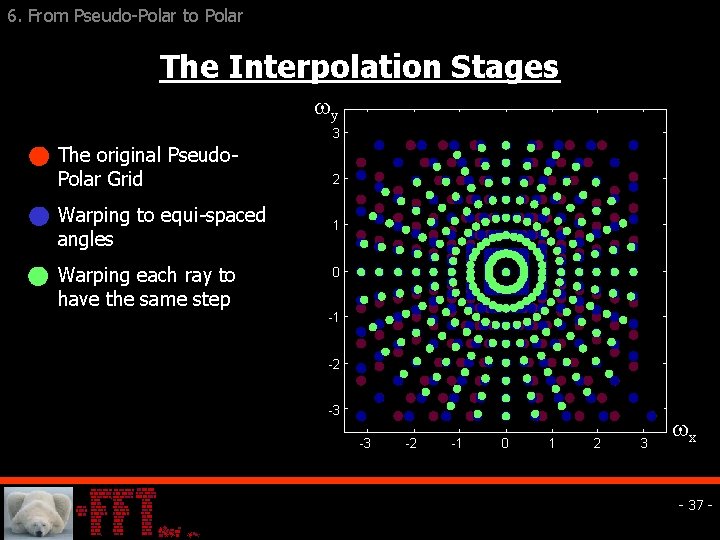
6. From Pseudo-Polar to Polar The Interpolation Stages y 3 The original Pseudo. Polar Grid Warping to equi-spaced angles Warping each ray to have the same step 2 1 0 -1 -2 -3 -3 -2 -1 0 1 2 3 x - 37 -

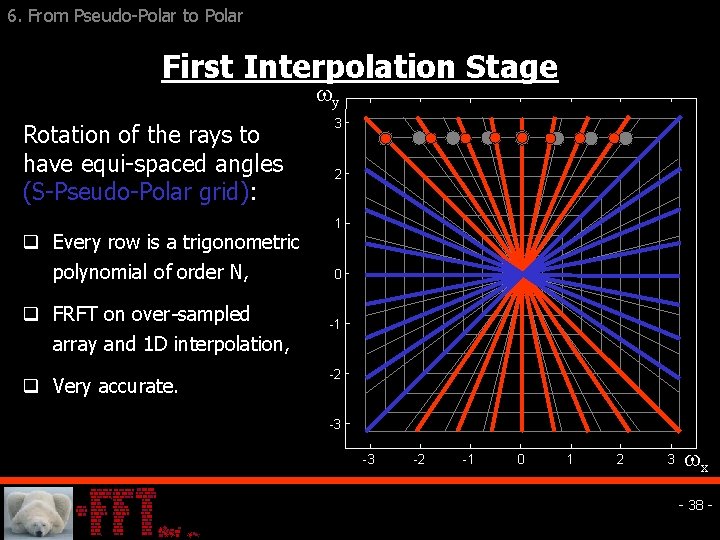
6. From Pseudo-Polar to Polar First Interpolation Stage y Rotation of the rays to have equi-spaced angles (S-Pseudo-Polar grid): q Every row is a trigonometric polynomial of order N, q FRFT on over-sampled array and 1 D interpolation, q Very accurate. 3 2 1 0 -1 -2 -3 -3 -2 -1 0 1 2 3 x - 38 -

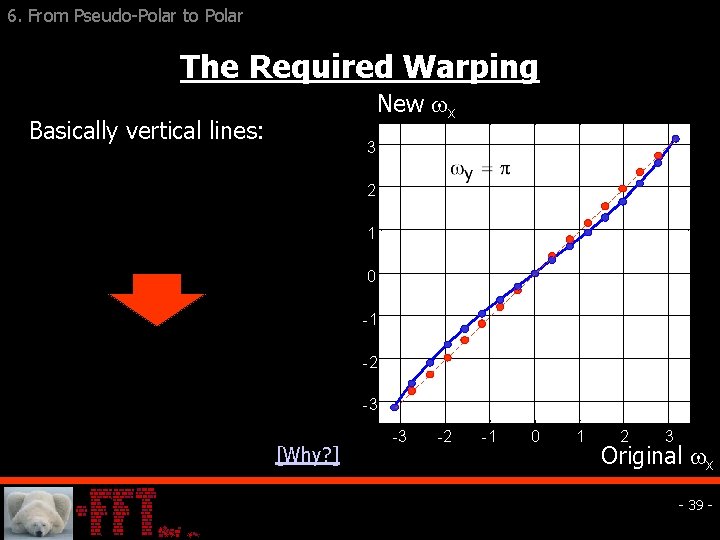
6. From Pseudo-Polar to Polar The Required Warping New x Basically vertical lines: 3 2 1 0 -1 -2 -3 [Why? ] -3 -2 -1 0 1 2 3 Original x - 39 -

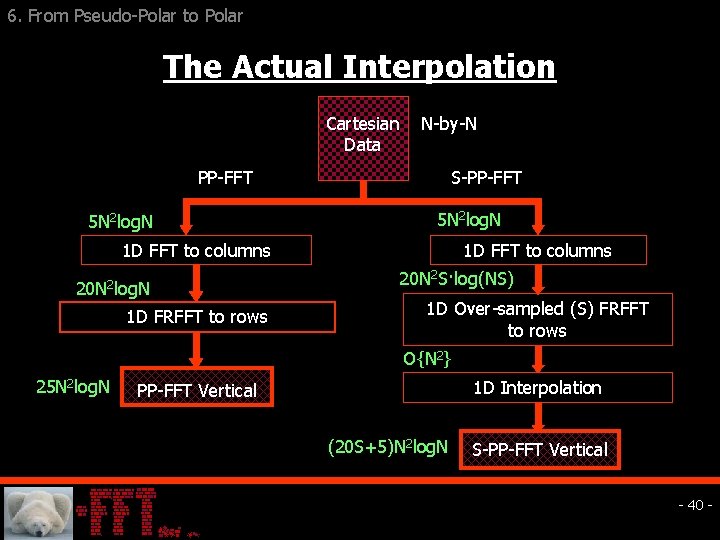
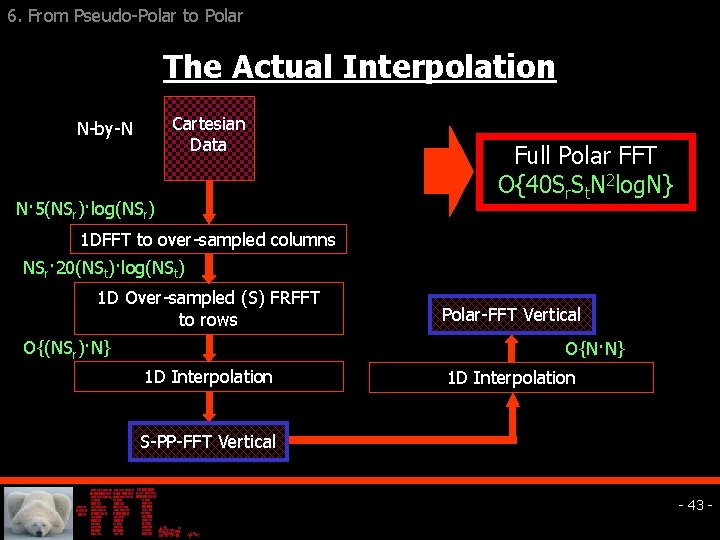
6. From Pseudo-Polar to Polar The Actual Interpolation Cartesian N-by-N Data PP-FFT 5 N 2 log. N S-PP-FFT 5 N 2 log. N 1 D FFT to columns 20 N 2 log. N 1 D FRFFT to rows 1 D FFT to columns 20 N 2 S·log(NS) 1 D Over-sampled (S) FRFFT to rows O{N 2} 25 N 2 log. N 1 D Interpolation PP-FFT Vertical (20 S+5)N 2 log. N S-PP-FFT Vertical - 40 -

6. From Pseudo-Polar to Polar Second Interpolation Stage y q As opposed to the previous step, the rays are not trigonometric polynomials of order N, q We proved that the rays are band-limited (smooth) functions, q Over-sampling and interpolation is expected to perform well. 3 2 1 0 -1 -2 -3 -3 -2 -1 0 1 2 3 x - 41 -

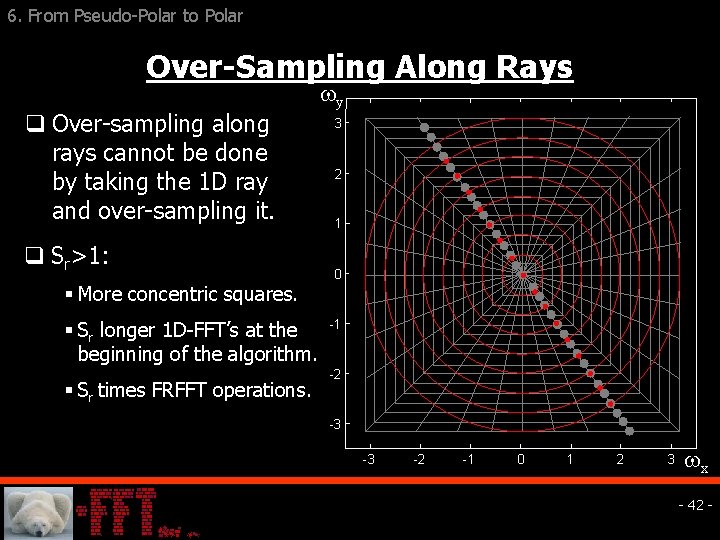
6. From Pseudo-Polar to Polar Over-Sampling Along Rays q Over-sampling along rays cannot be done by taking the 1 D ray and over-sampling it. q Sr>1: § More concentric squares. § Sr longer 1 D-FFT’s at the beginning of the algorithm. § Sr times FRFFT operations. y 3 2 1 0 -1 -2 -3 -3 -2 -1 0 1 2 3 x - 42 -

6. From Pseudo-Polar to Polar The Actual Interpolation Cartesian Data N-by-N N· 5(NSr)·log(NSr) Full Polar FFT O{40 Sr. St. N 2 log. N} 1 DFFT to over-sampled columns NSr· 20(NSt)·log(NSt) 1 D Over-sampled (S) FRFFT to rows O{(NSr)·N} Polar-FFT Vertical O{N·N} 1 D Interpolation S-PP-FFT Vertical - 43 -

6. From Pseudo-Polar to Polar To Summarize We propose a Fast Polar Fourier Transform with the following features: § Low complexity – O(Const·N 2 log 2 N) § Vectorizability – 1 D operations only § Non-Expansiveness – Factor 2 (or 4) only § Stability – via Regularization § Accuracy – 2 orders of magnitude over USFFT methods - 44 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 45 -

7. Algorithm Analysis We have a code performing the Polar-FFT in Matlab: Y=Polar_FFT(X); OR Y=Polar_FFT(X, St, Sr); Where: X – Input array of N-by-N samples St, Sr – Over-sampling factors in the approximations Y – Polar-FFT result as an 2 N-by-2 N array with rows being the rays and columns being the concentric circles. - 46 -

7. Algorithm Analysis The Implementation q The current Polar-FFT code implements Taylor method for the first interpolation stage and spline ONLY (no-derivatives) for the second stage. q For comparison, we demonstrate the performance of the USFFT method with over-sampling S and interpolation based on the Taylor interpolation (found to be the best). - 47 -

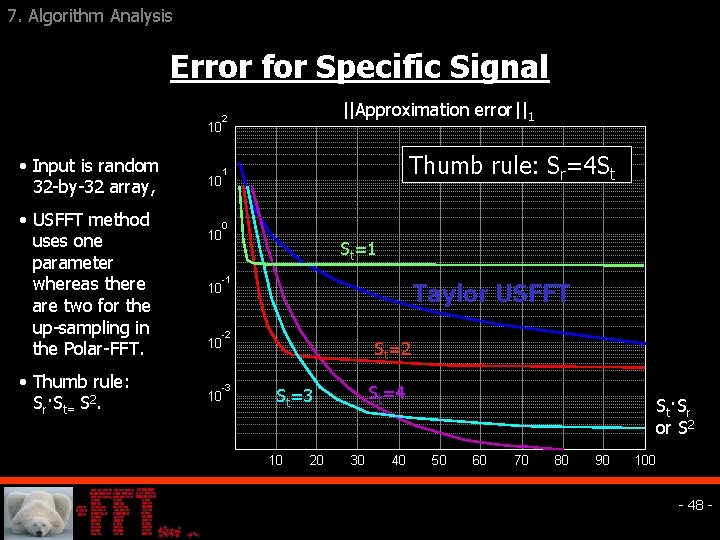
7. Algorithm Analysis Error for Specific Signal ||Approximation error||1 2 10 • Input is random 32 -by-32 array, • USFFT method uses one parameter whereas there are two for the up-sampling in the Polar-FFT. • Thumb rule: Sr·St= S 2. Thumb rule: Sr=4 St 1 10 0 10 St=1 -1 Taylor USFFT 10 -2 10 -3 10 St=2 St=4 St=3 10 20 30 40 St·Sr or S 2 50 60 70 80 90 100 - 48 -

7. Algorithm Analysis Error For Specific Signals q Similar curves obtained of ||*|| and ||*||2 norms. q Similar behavior is found for other signals. q Conclusion: For the proper choice of St and Sr, we get 2 -orders-of-magnitude improvement in the accuracy comparing to the best USFFT method. q Further improvement should be achieved for Taylor interpolation in the second stage. q US-FFT takes longer due the 2 D operations. - 49 -

7. Algorithm Analysis The Transform as a Matrix Approximate All the involved transformations (accurate and approximate) are linear - they can be represented as a matrix of size 4 N 2 -by. N 2. Ya=Ax Or Yt=Tx True - 50 -

7. Algorithm Analysis Regularization of T/A q An input signal of N-by-N is transformed to an array or 2 N-by-2 N. q For N=16, T size is 1024 -by-256, and 60, 000 (bad for inversion). q Adding the assumption that the Frequency corners should be zeroed, we obtain and the condition number becomes 5 !!! - 51 -

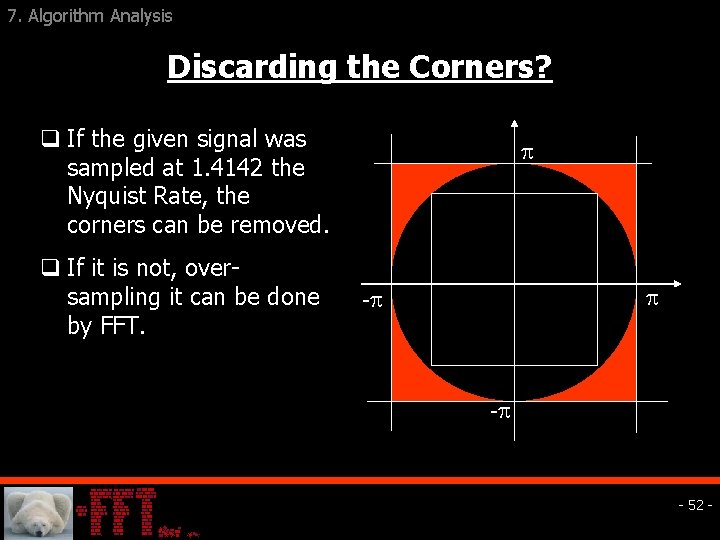
7. Algorithm Analysis Discarding the Corners? q If the given signal was sampled at 1. 4142 the Nyquist Rate, the corners can be removed. q If it is not, oversampling it can be done by FFT. - - - 52 -

7. Algorithm Analysis Error Analysis – Worst Signal Approximation error is : Worst error : Worst relative error : - 53 -

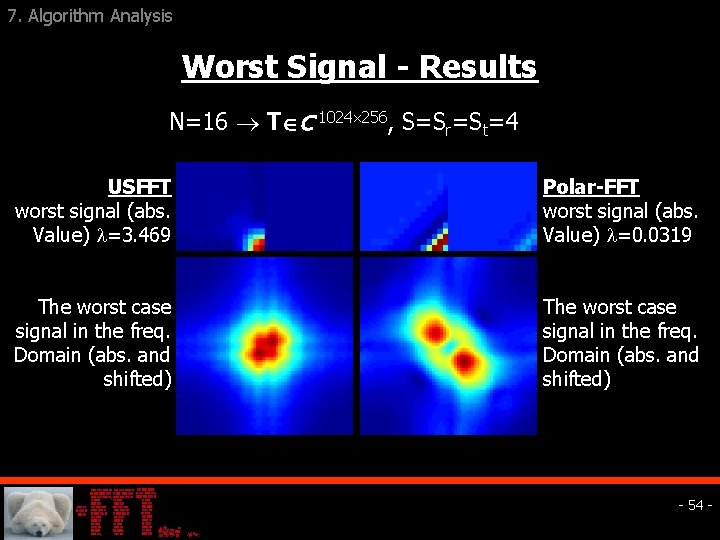
7. Algorithm Analysis Worst Signal - Results N=16 T C 1024 256, S=Sr=St=4 USFFT worst signal (abs. Value) =3. 469 Polar-FFT worst signal (abs. Value) =0. 0319 The worst case signal in the freq. Domain (abs. and shifted) - 54 -

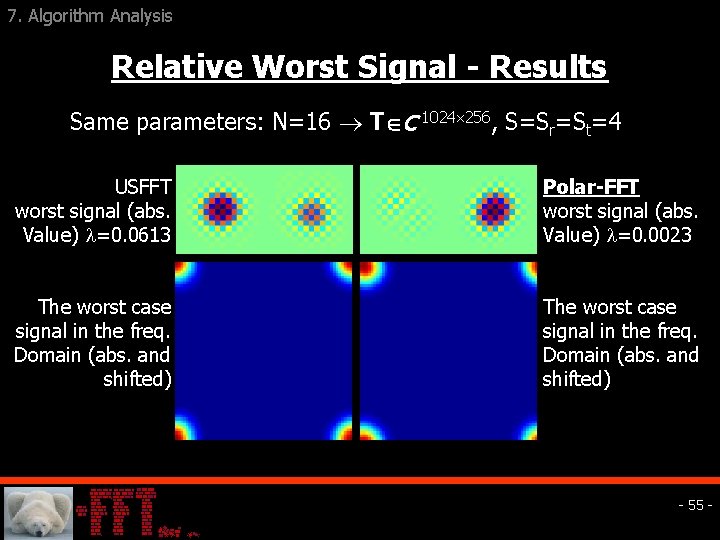
7. Algorithm Analysis Relative Worst Signal - Results Same parameters: N=16 T C 1024 256, S=Sr=St=4 USFFT worst signal (abs. Value) =0. 0613 Polar-FFT worst signal (abs. Value) =0. 0023 The worst case signal in the freq. Domain (abs. and shifted) - 55 -

7. Algorithm Analysis Comparing Approximations q Solve for the eigenvalue/vectors of the matrix and obtained ( in ascending order). q Compare to by computing using the above eigenvectors and compare to . - 56 -

7. Algorithm Analysis Comparing Approximations - Results 2 10 Mean Squared Error [N=32] 0 10 USFFT -2 10 -4 10 -6 10 Polar-FFT -8 Eigen-space of the Polar. FFT 10 -10 10 0 200 400 600 800 1000 1200 - 57 -

Agenda 1. Thinking Polar – Continuum 2. Thinking Polar – Discrete 3. Current State-Of-The-Art 4. Our Approach - General 5. The Pseudo-Polar Fast Transform 6. From Pseudo-Polar to Polar 7. Algorithm Analysis 8. Conclusions - 58 -

8. Conclusions q We have proposed a fast, accurate, stable, and reliable Polar Discrete-Fourier-Transform. q By this we extend utility of FFT algorithms to new class of settings in image processing. q Future plans: § Extend the analysis and improve further, § Demonstrate applications, § Publish the code for the procedure and some applications over the internet. - 59 -

Beyond this slides are the appendix or redundant slides - 60 -

3. Current State-of-the-Art USFFT for T† q Over-sample Polar grid (and possibly partial derivatives). q Associate polar neighbors to each Cartesian grid point. q Approximate interpolation to get the Cartesian grid values. q Perform the Cartesian 2 D Inverse-FFT. - 61 -

3. Current State-of-the-Art Our Reading of Literature Direct Fourier method with over-sampling and interpolation (also called gridding) – see q Natterer (1985). q Jackson, Meyer, Nishimura and Macovski (1991). q Schomberg and Timmer (1995). q Choi and Munson (1998). - 62 -

A. The Fractional Fourier Transform The Pseudo-Polar Sampling Basically vertical lines: y 3 2 1 0 -1 -2 For St=Sr=1, we have N 2 grid points -3 -3 -2 -1 0 1 2 3 x - 63 -

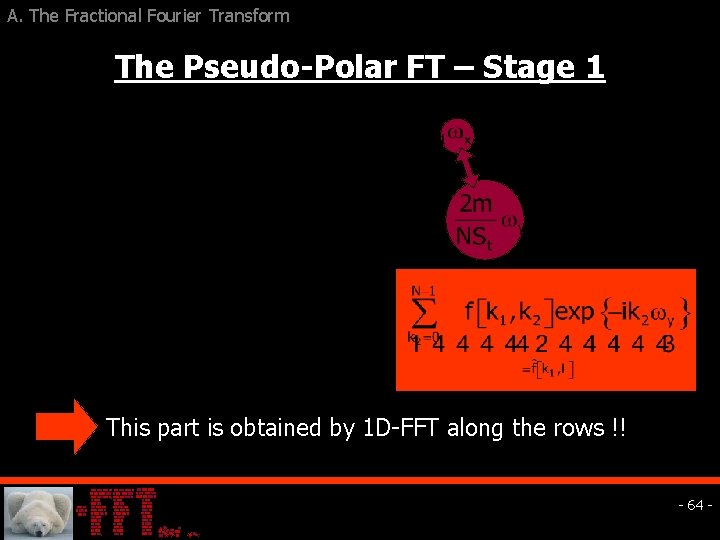
A. The Fractional Fourier Transform The Pseudo-Polar FT – Stage 1 This part is obtained by 1 D-FFT along the rows !! - 64 -

A. The Fractional Fourier Transform The Pseudo-Polar FT – Stage 2 q This summation takes columns of (being equispaced 1 D signals) and computes Fourier transform of it. q The destination grid points are also 1 D equi-spaced in the frequency domain, BUT THEY ARE NOT IN THE RANGE [- , ], but rather [- y, y]. q This task is called Fractional Fourier/Chirp-Z Transform. - 65 -

A. The Fractional Fourier Transform q For =1 we get the ordinary 1 D-FFT, q For =-1 we get the ordinary 1 D-IFFT, q There exists a Fast Fractional Fourier Transform with the complexity of O(20·Nlog 2 N), based on 1 D-FFT operations. See: Fast fractional Fourier transforms and applications, by D. H. Bailey and P. N. Swarztrauber, SIAM Review, 1991, and also Bluestein, Rabiner, and Rader (1960’s). - 66 -

A. The Fractional Fourier Transform FR-FFT Detailed Post Multiplication Pre-Multiplication Convolution [Back] - 67 -

B. From Pseudo-Polar to Polar Interpolation As 1 D Operation q It is a 1 D operation – But it is not the Fractional-FFT. q Can be computed by over-sampled FRFFT and interpolation. - 68 -