Fast orbit bump magnet Use of magnetic field

Fast orbit bump magnet • Use of magnetic field varying with time Multi-turn septum injection Orbit shift for phase-space painting of H- injection • Use of pulse magnetic field at the peak value Orbit shift close to the septum magnet for a fast extraction • Use of pulse magnetic field at flat-top Chicane bump for H- injection Orbit shift close to the septum magnet for a slow extraction 1

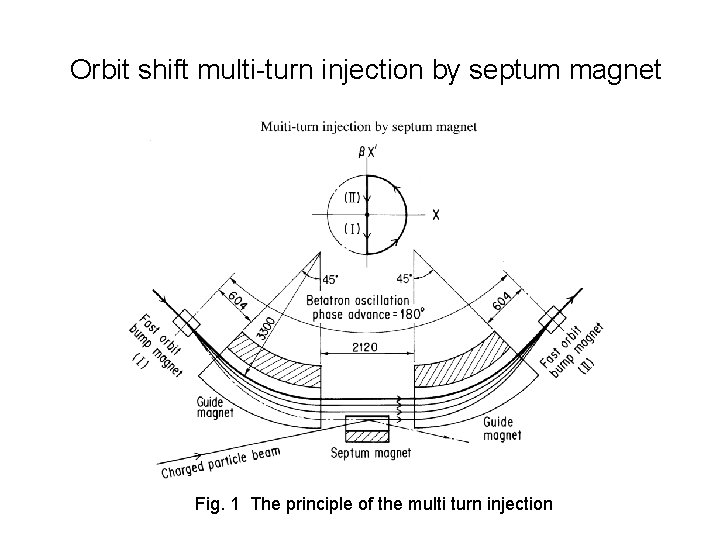
Orbit shift multi-turn injection by septum magnet Fig. 1 The principle of the multi turn injection

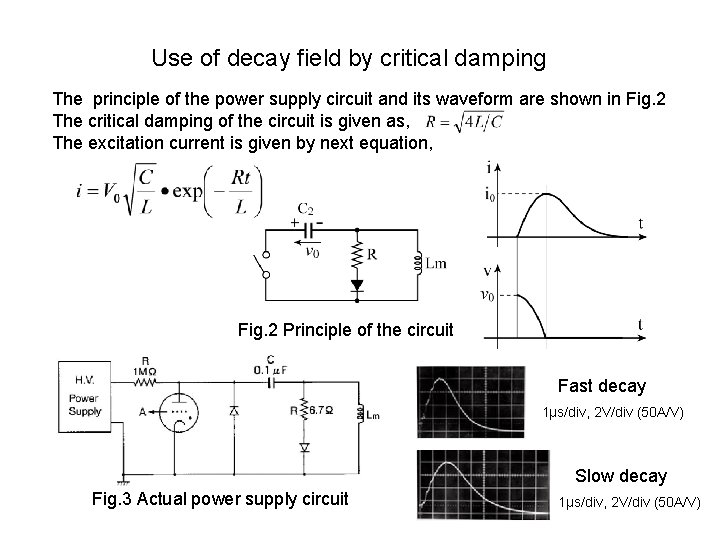
Use of decay field by critical damping The principle of the power supply circuit and its waveform are shown in Fig. 2 The critical damping of the circuit is given as, The excitation current is given by next equation, Fig. 2 Principle of the circuit Fast decay 1μs/div, 2 V/div (50 A/V) Slow decay Fig. 3 Actual power supply circuit 1μs/div, 2 V/div (50 A/V)

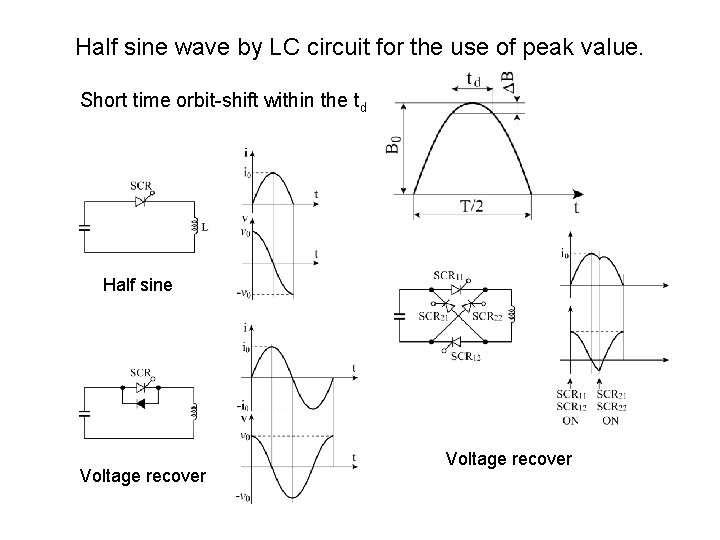
Half sine wave by LC circuit for the use of peak value. Short time orbit-shift within the td Half sine Voltage recover

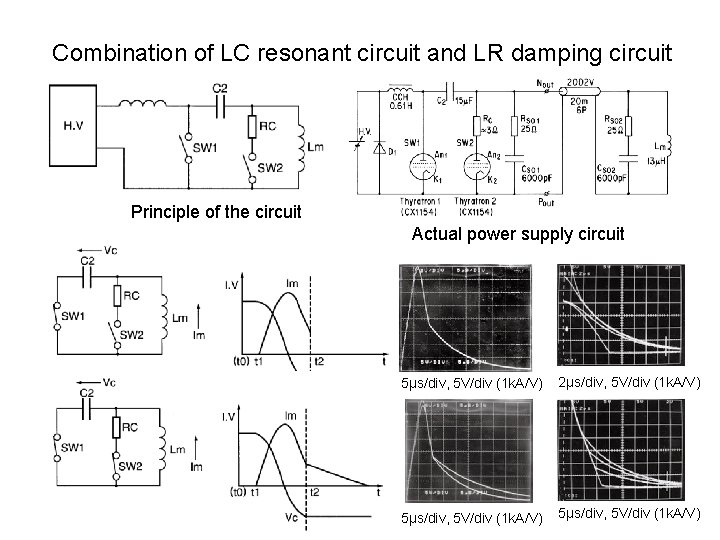
Combination of LC resonant circuit and LR damping circuit Principle of the circuit Actual power supply circuit 5μs/div, 5 V/div (1 k. A/V) 2μs/div, 5 V/div (1 k. A/V) 5μs/div, 5 V/div (1 k. A/V)

Fast orbit bump magnet for orbit shift multi-turn injection • Fast decay time (3~6 μs) • Ferrite is used for the core material. • Swing of the magnetic field is not allowed (for injection)

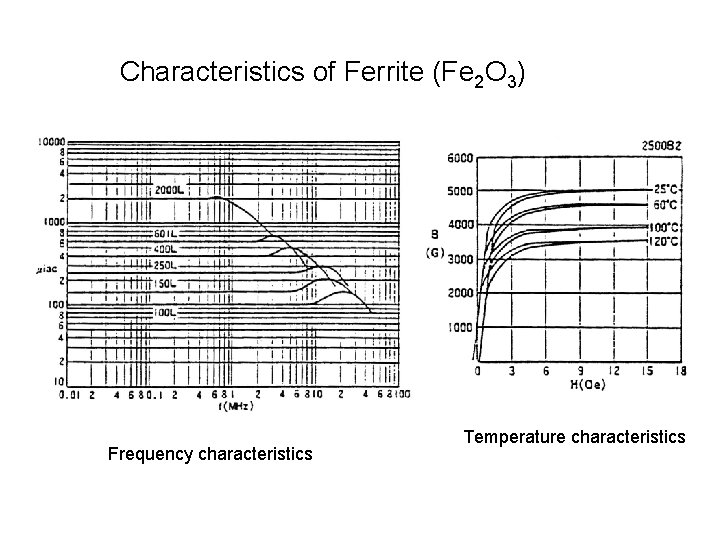
Characteristics of Ferrite (Fe 2 O 3) Frequency characteristics Temperature characteristics

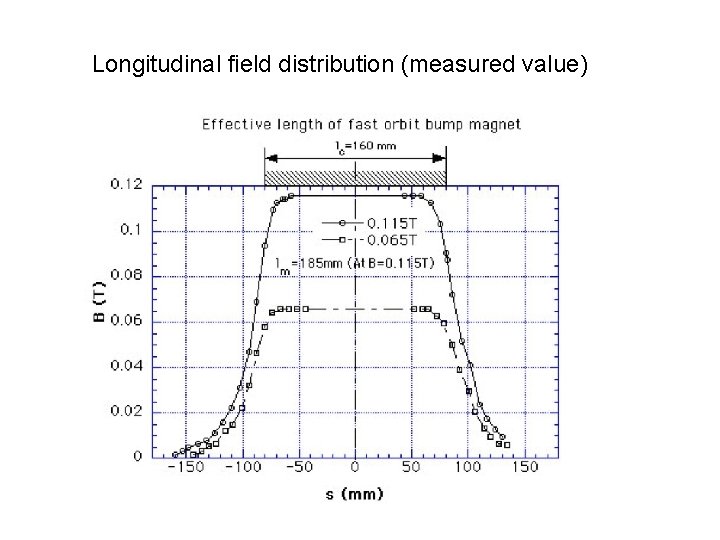
Longitudinal field distribution (measured value)

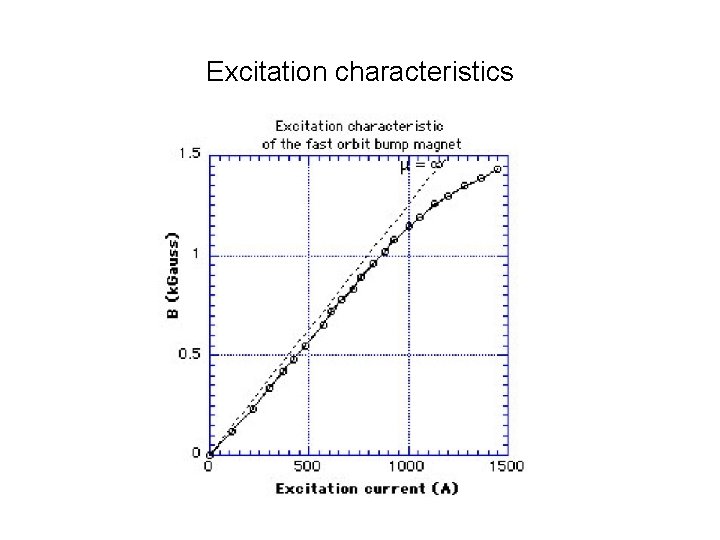
Excitation characteristics

Caution ! For “window frame” and “H-type core” • Shorted-magnetic circuit enclose the beam. • Magnetic resistance is very low. • Strong magnetic field is induced around bunched beams. • Open-magnetic circuit • Magnetic resistance is high. • Magnetic field induced around bunched beams is low. C-type is better !

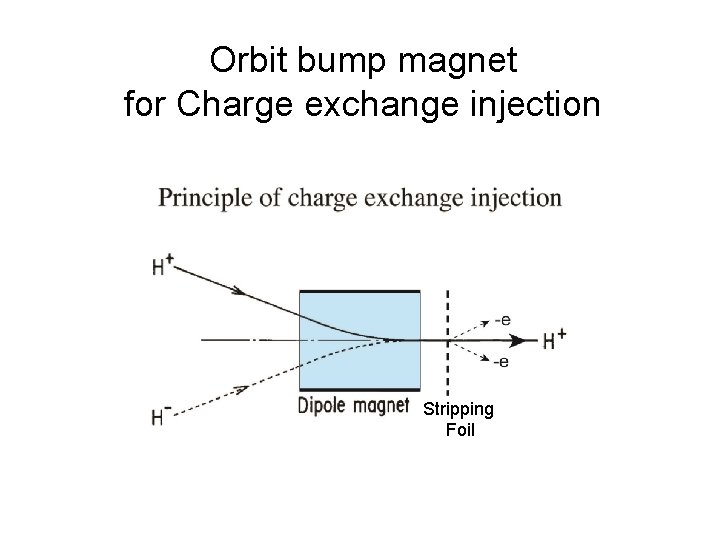
Orbit bump magnet for Charge exchange injection Stripping Foil

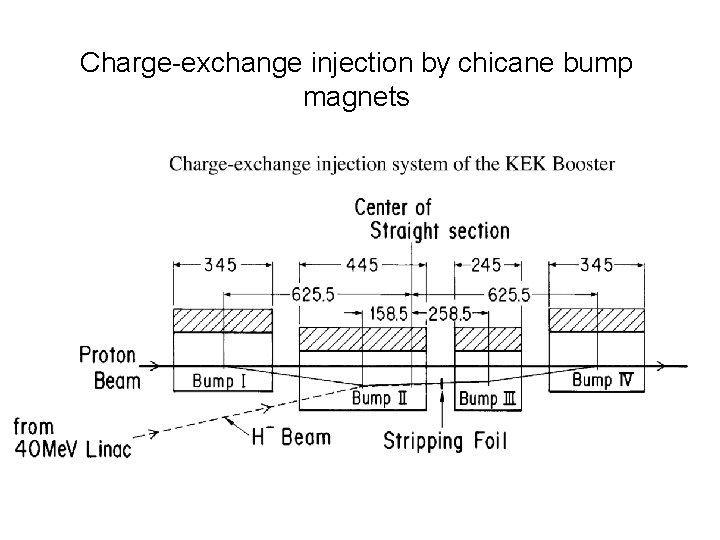
Charge-exchange injection by chicane bump magnets

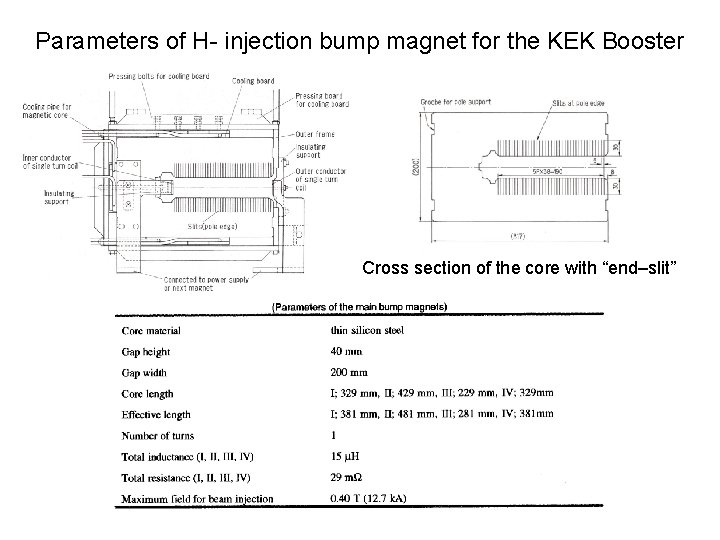
Parameters of H- injection bump magnet for the KEK Booster Cross section of the core with “end–slit”

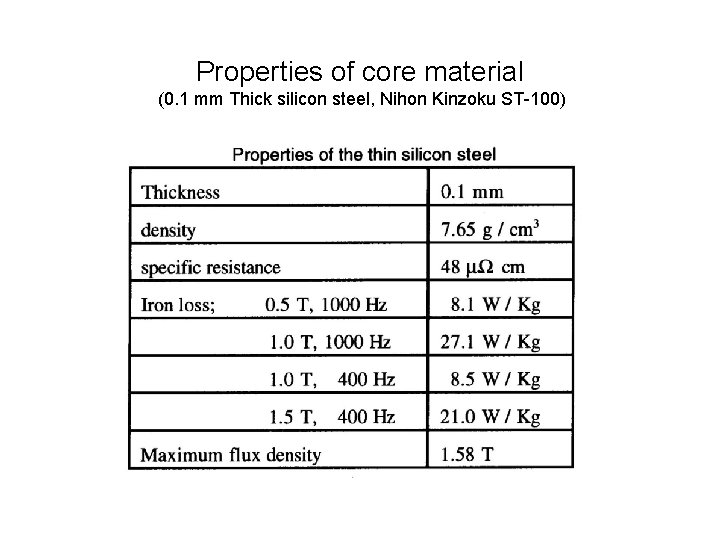
Properties of core material (0. 1 mm Thick silicon steel, Nihon Kinzoku ST-100)

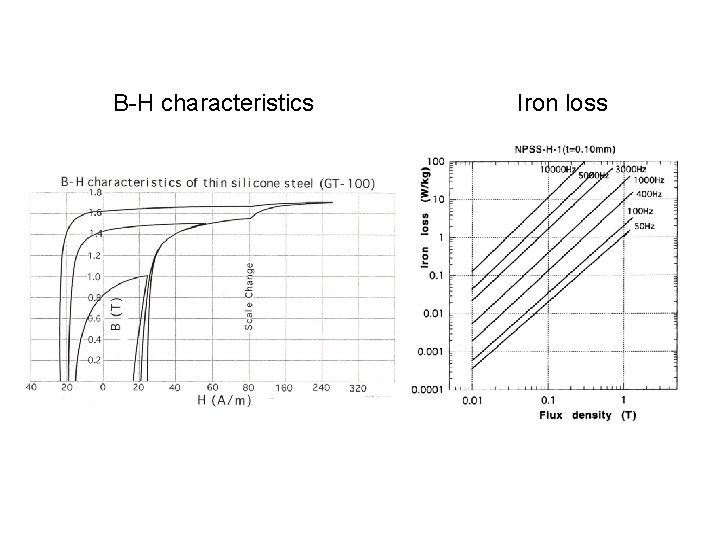
B-H characteristics Iron loss

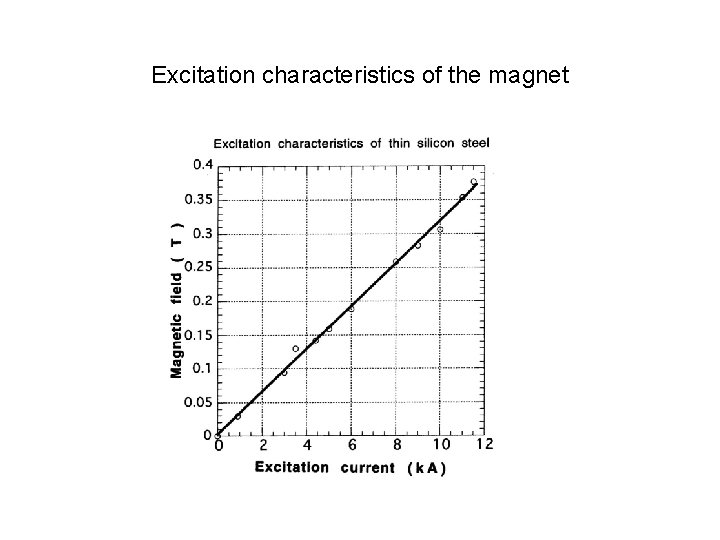
Excitation characteristics of the magnet

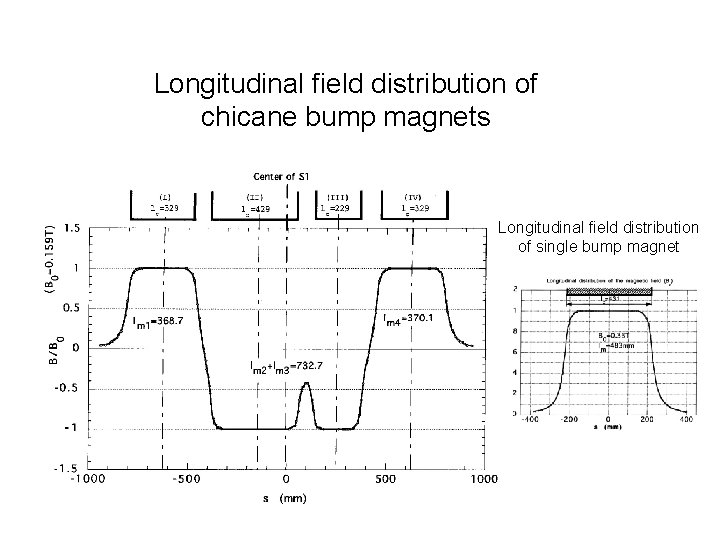
Longitudinal field distribution of chicane bump magnets Longitudinal field distribution of single bump magnet

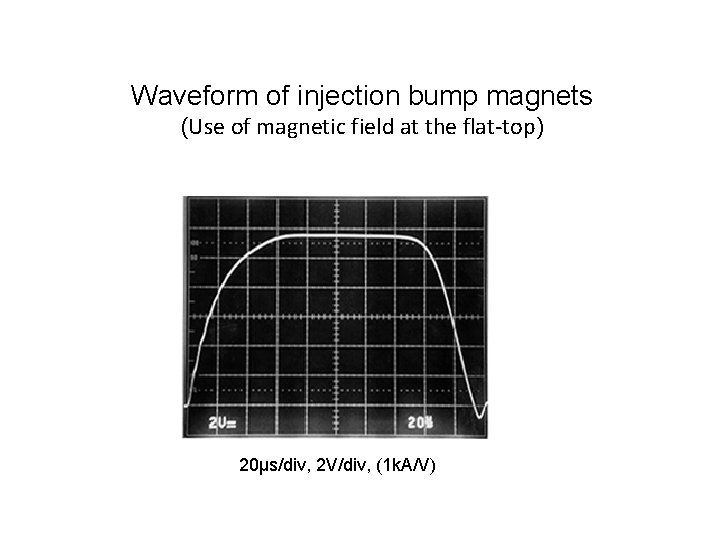
Waveform of injection bump magnets (Use of magnetic field at the flat-top) 20μs/div, 2 V/div, (1 k. A/V)

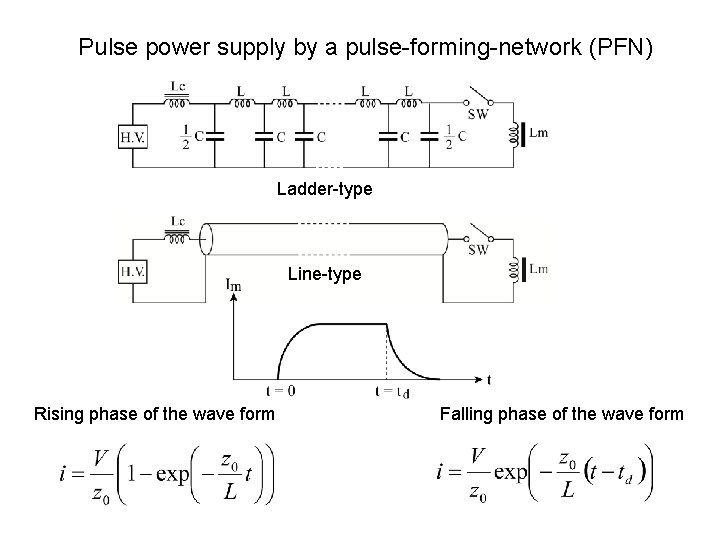
Pulse power supply by a pulse-forming-network (PFN) Ladder-type Line-type Ladder-type Rising phase of the wave form Falling phase of the wave form

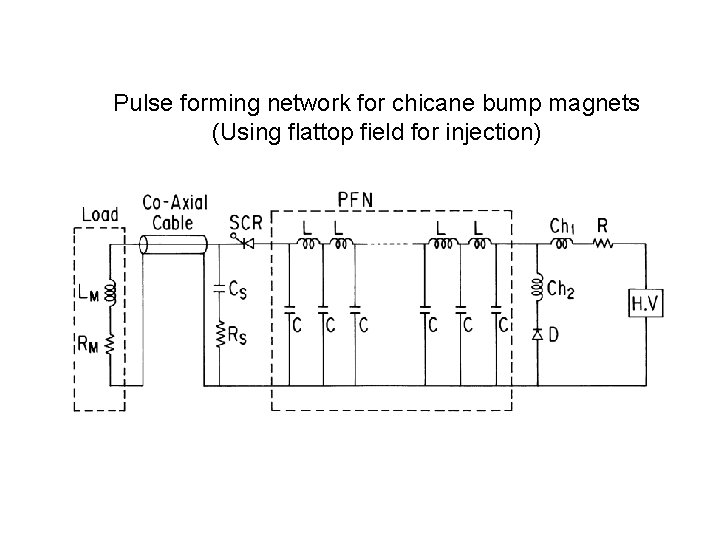
Pulse forming network for chicane bump magnets (Using flattop field for injection)

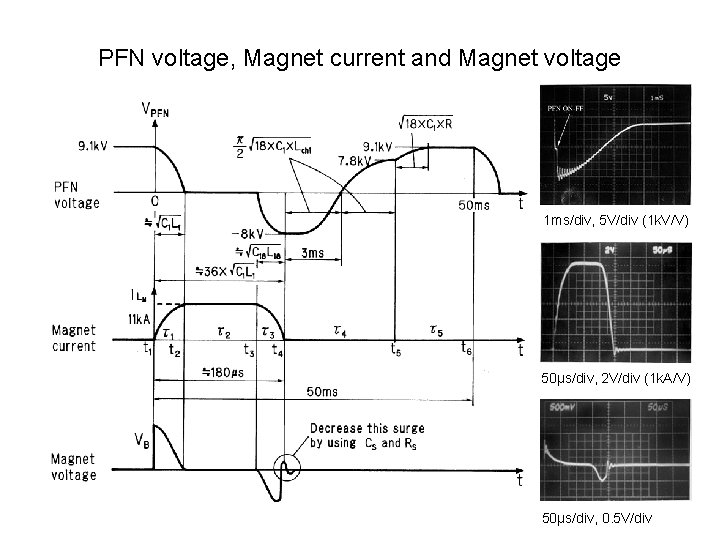
PFN voltage, Magnet current and Magnet voltage 1 ms/div, 5 V/div (1 k. V/V) 50μs/div, 2 V/div (1 k. A/V) 50μs/div, 0. 5 V/div

Fundamentals of Transmission Line Theory “Exact transitional solution” Let’s consider the part of transmission line as, x x + Δx On the one side line, partial resistance and inductance per unit length are (R/2) and (L/2) respectively. By the go and the return the values become R and L. The capacitance and conductance between two lines are defined as C and G respectively.

Equations for v and i are given as, finite difference equation. (1) Divide both sides by Δx and in the limit of Δx→ 0, we can get next differential equations. (2) These simultaneous partial differential equations are known as “Telegraphy equation”

In the case of lossless transmission line, i. e. R = G = 0. The telegraphy equation becomes Here, (3) We can get wave equations. Here (4) The solution of Eq. (4) is given as, (5) v and i must satisfy the Eq. (3), we can get next solution for i, (6)

Eq. (5) and (6) satisfies wave equation. Final solution can be obtained by initial condition of “t” and boundary condition of “x”. Here we define the initial value of “v” and “t“ as v(x, 0) and i(x, 0) respectively. Then we perform Laplace transformation for Eq. (3) and (4). (7) (8) For the case of initial values are zero. (or v(x, 0)=0 and i(x, 0)=0 ) (9) Eq. (9) is equivalent to Eq. (5) and Eq. (6).

In the Eq. (9), V 1 and V 2 are decided by boundary condition of the x. When a voltage source e(t) is connected at x=0, The Laplace transformation of e(t) is written as, L{e(t)}=E(s). For a current source i(t), it is also as, L{i(t)}=I(s). Those are, at x=0, the voltage source e(t) is connected; V(0, s)=E(s) at x=0, the current source i(t) is connected; I(0, s)=I(s) The length of the transmission line is “ l ” at x=l, the terminal is shorten; V(l, s)=0 at x=l, the terminal is open; I(l, s)=0 at x=l, Z(s) is connected; V(l, s) / I(l, s)=Z(s) For example, a voltage source e(t) with internal impedance Z 0(s) are connected at x=0 as shown in Fig. The conditional equation is,

Terminal is shorted-circuit as in Fig. A electromotive force is connected at x=0, and the terminal at x=l is shortened. The boundary condition is, at x=0 ; V(0, s)=E(s) at x=l ; V(l, s)=0 From Eq. (9) first, (10) We can solve Eq. (10) for V 1 and V 2, and substitute them to Eq. (9), the Laplace transform of the voltage v and current I is calculated as, (11) Here, (characteristic impedance) (12)

After rearrangement of the Eq. (11), then expand it in a series, (13) By the same procedure, we can get the I(x, s) as, (14) By inverse Laplace transformation (15)

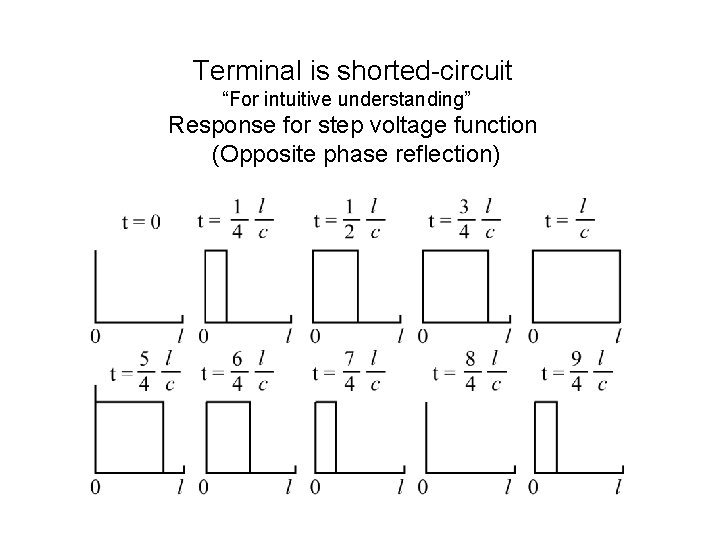
Terminal is shorted-circuit “For intuitive understanding” Response for step voltage function (Opposite phase reflection)

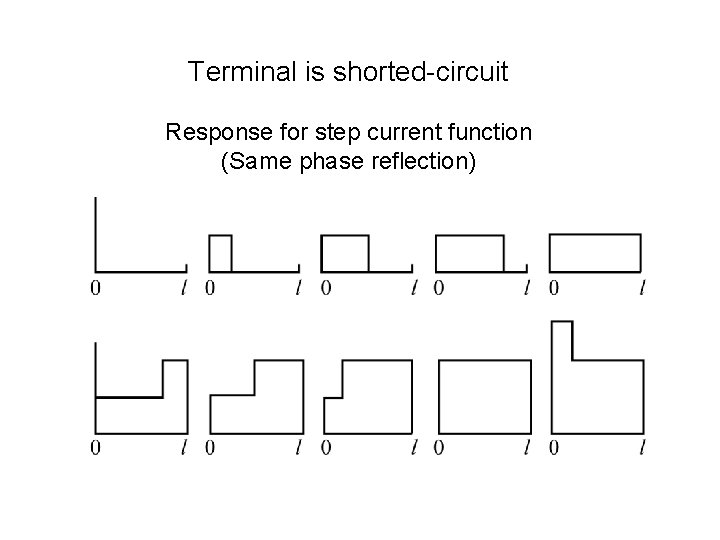
Terminal is shorted-circuit Response for step current function (Same phase reflection)

Terminal is open circuit as in Fig. A electromotive force is connected at x=0, and the terminal at x=l is opened. The boundary condition is, (16) We can solve Eq. (16) for V 1 and V 2, and substitute them to Eq. (9), the Laplace transform of the voltage v and current I is calculated. Then expand it in a series and next by inverse Laplace transformation, we can get v(x, t) and i(x, t) as, (17)

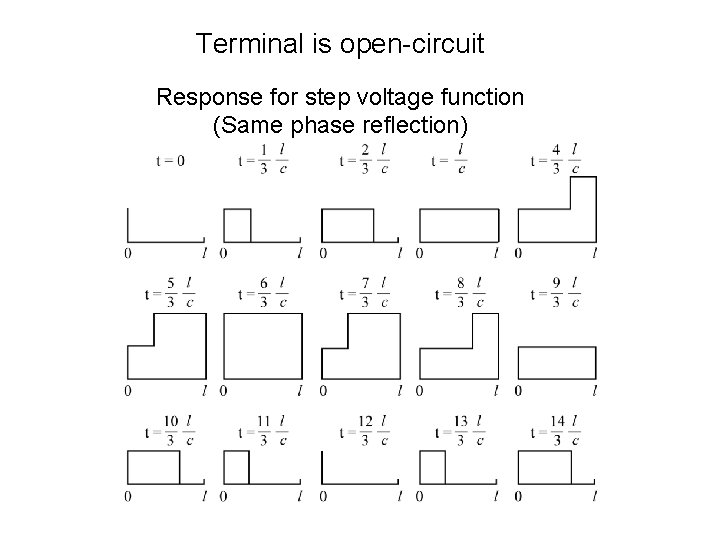
Terminal is open-circuit Response for step voltage function (Same phase reflection)

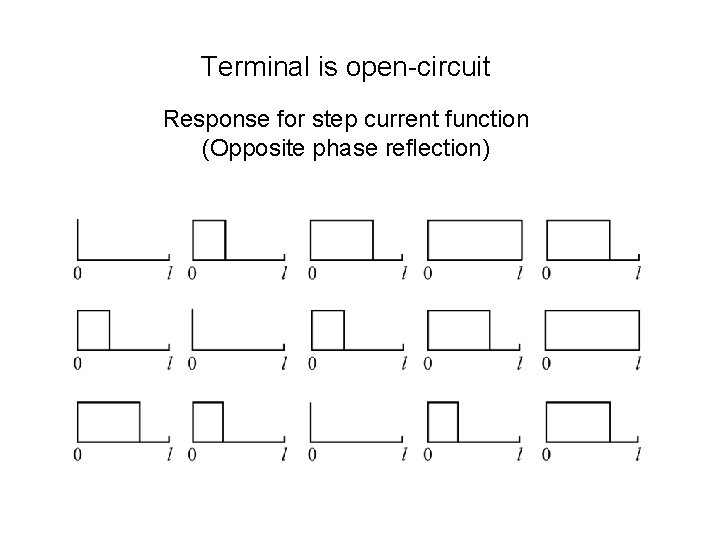
Terminal is open-circuit Response for step current function (Opposite phase reflection)

Z(s) is connected to the terminal. The boundary condition is, Here, we set Z(s)=R for the simplicity. W is the characteristic impedance.

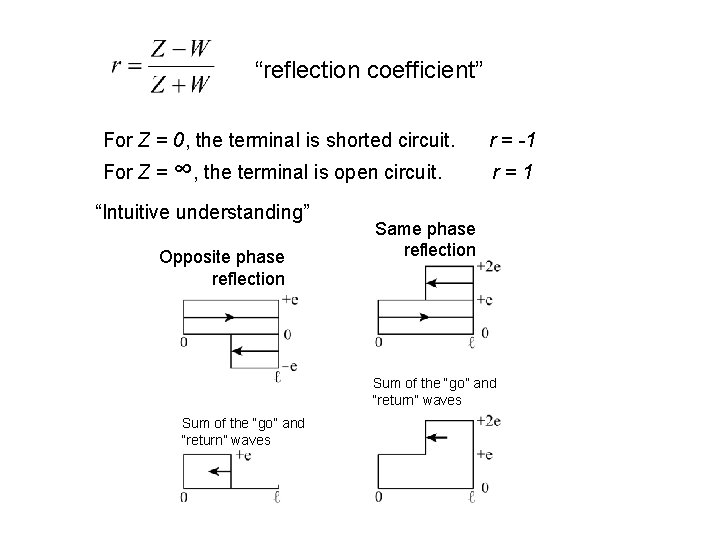
“reflection coefficient” For Z = 0, the terminal is shorted circuit. r = -1 For Z = ∞, the terminal is open circuit. r=1 “Intuitive understanding” Opposite phase reflection Same phase reflection Sum of the “go” and “return” waves

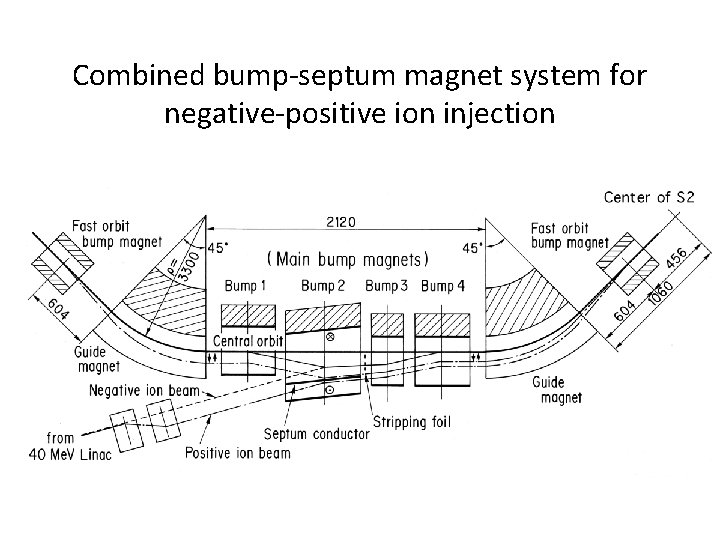
Combined bump-septum magnet system for negative-positive ion injection

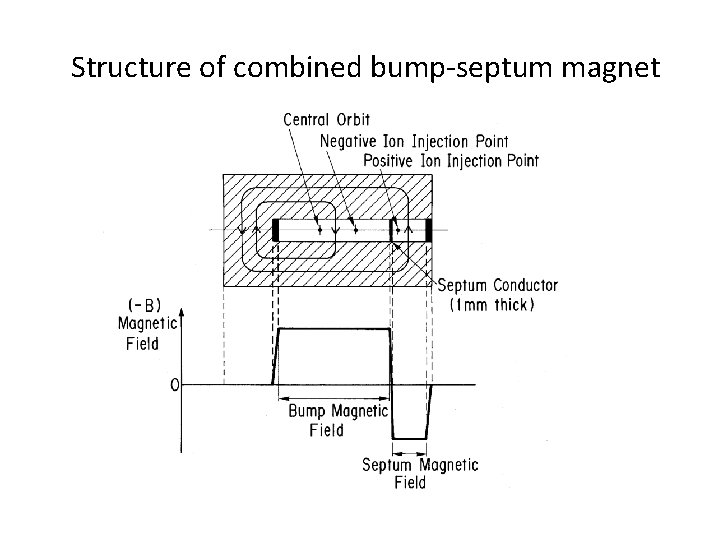
Structure of combined bump-septum magnet

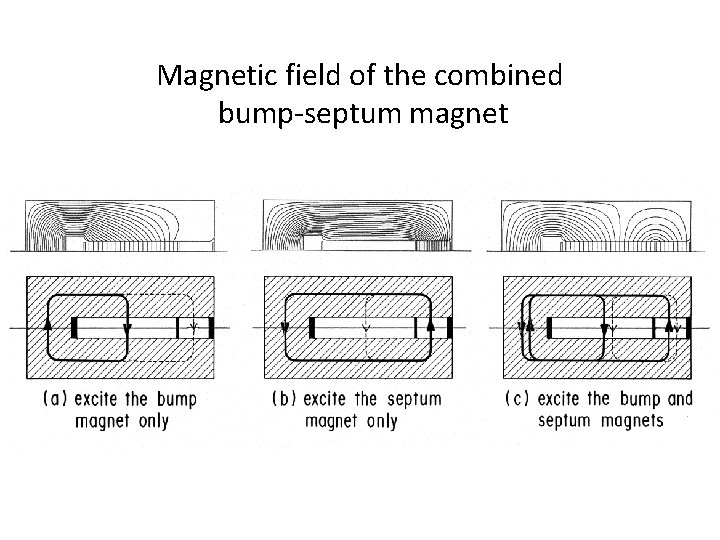
Magnetic field of the combined bump-septum magnet

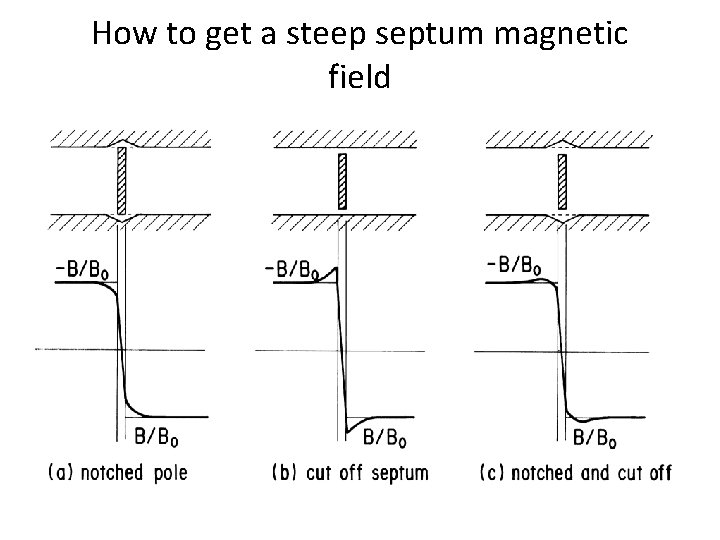
How to get a steep septum magnetic field

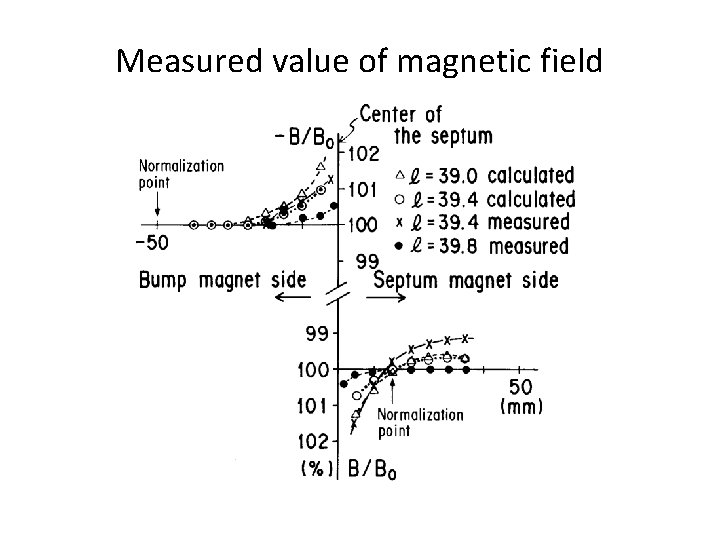
Measured value of magnetic field

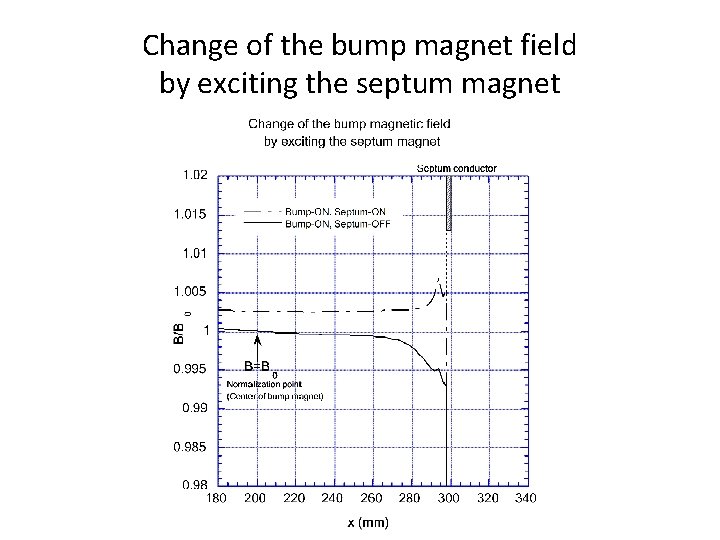
Change of the bump magnet field by exciting the septum magnet

Figure of combined bump-septum magnet

Figure of combined bump-septum magnet

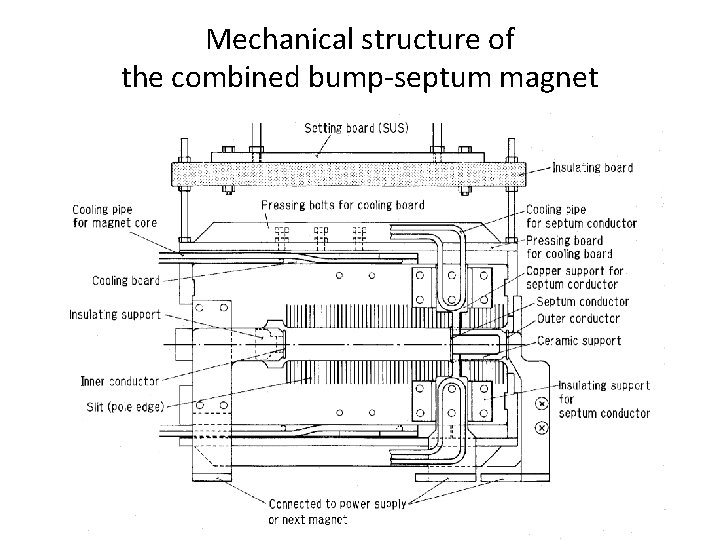
Mechanical structure of the combined bump-septum magnet

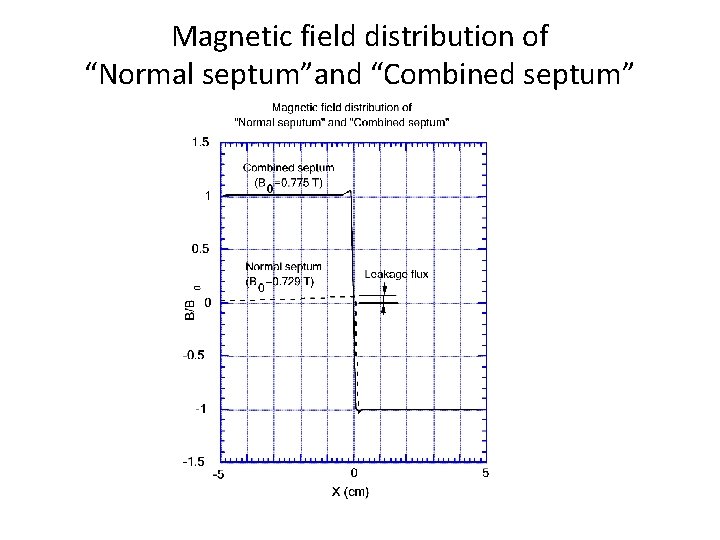
Magnetic field distribution of “Normal septum”and “Combined septum”

Comparison of “Normal septum”and “Combined septum”

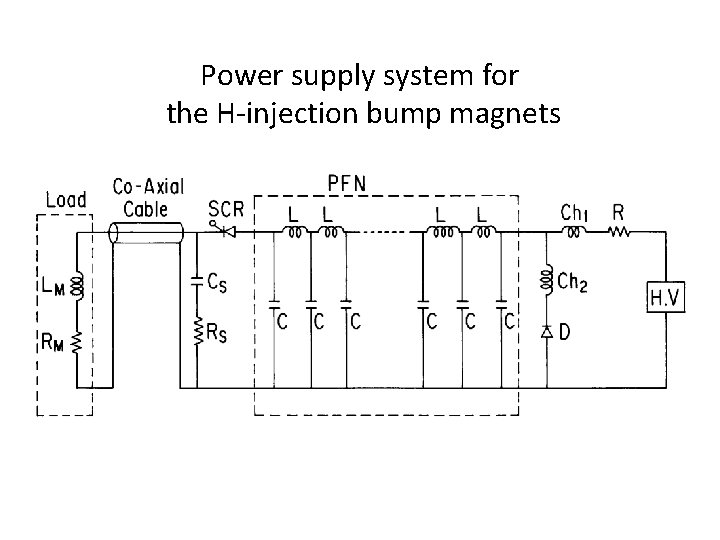
Power supply system for the H-injection bump magnets

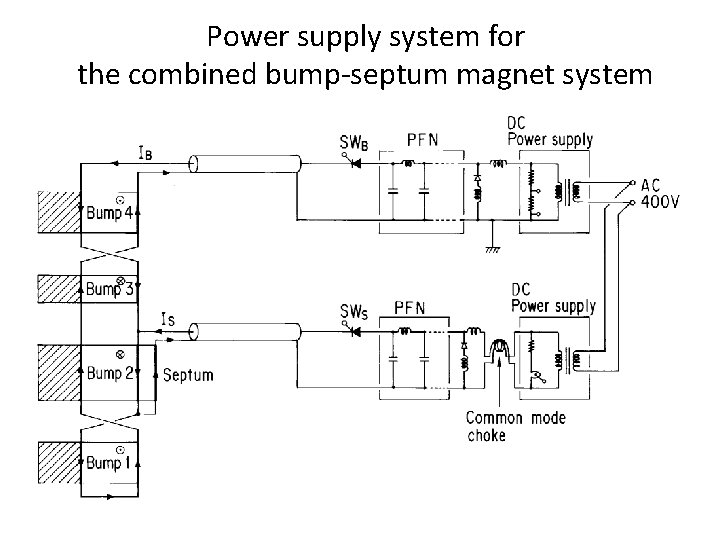
Power supply system for the combined bump-septum magnet system

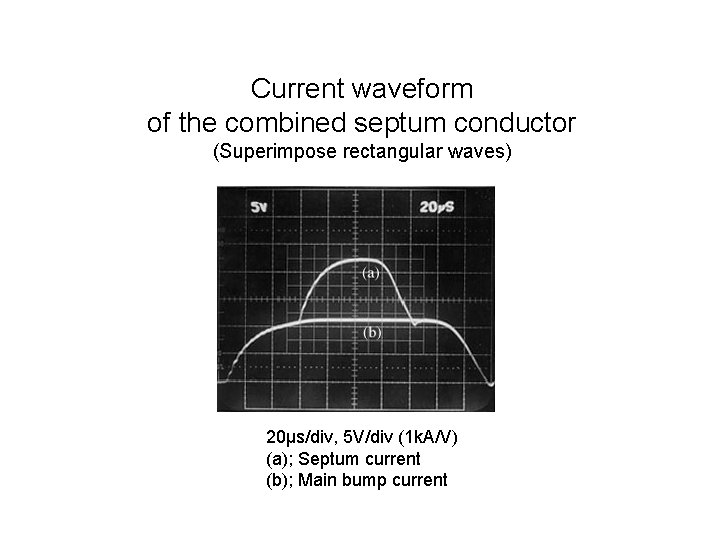
Current waveform of the combined septum conductor (Superimpose rectangular waves) 20μs/div, 5 V/div (1 k. A/V) (a); Septum current (b); Main bump current

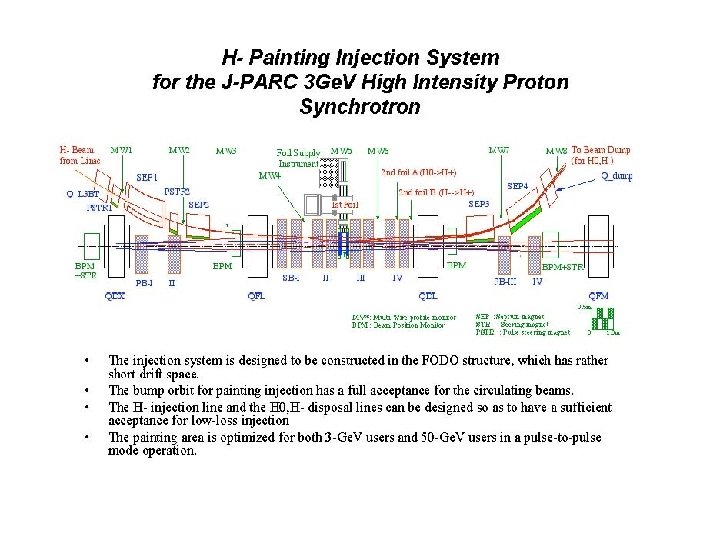
DESIGN OF THE MAGNETIC FIELD (For 400 -Me. V Injection) • In the upstream of the stripping foil The maximum magnetic field is estimated to be 0. 55 T The beam loss rate is less than 10 -6 The injection beam power is 133 k. W Losses by Lorentz stripping is less than 1. 3 W • In the downstream of the stripping foil The magnetic field of the bump magnet is set to be about 0. 2 T. Excited H 0 with a principal quantum number of n ≥ 6 becomes the uncontrolled beam Yield of n ≥ 6 is 0. 0136 The total H 0 beam power is 0. 4 k. W The maximum uncontrolled beam loss is about 6 W The magnetic field at the foil is designed to be less than the value at which the bending radius of the stripped electrons is larger than 100 mm.

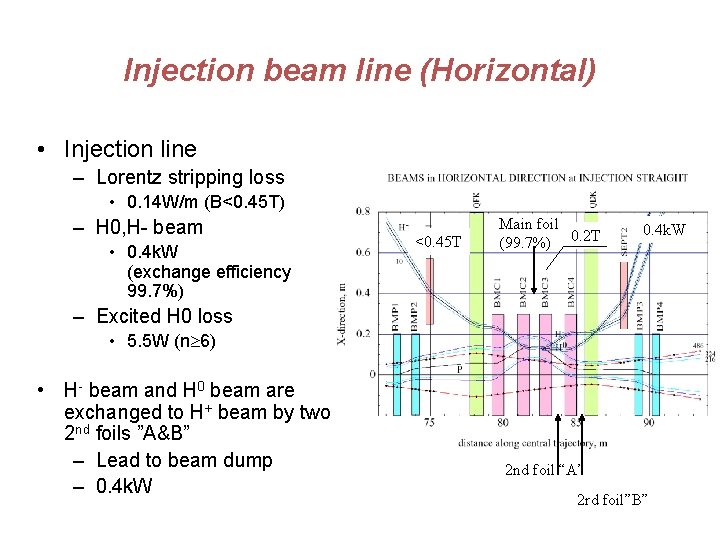
Injection beam line (Horizontal) • Injection line – Lorentz stripping loss • 0. 14 W/m (B<0. 45 T) – H 0, H- beam • 0. 4 k. W (exchange efficiency 99. 7%) <0. 45 T Main foil (99. 7%) 0. 2 T 0. 4 k. W – Excited H 0 loss • 5. 5 W (n 6) • H- beam and H 0 beam are exchanged to H+ beam by two 2 nd foils ”A&B” – Lead to beam dump – 0. 4 k. W 2 nd foil “A” 2 rd foil”B”

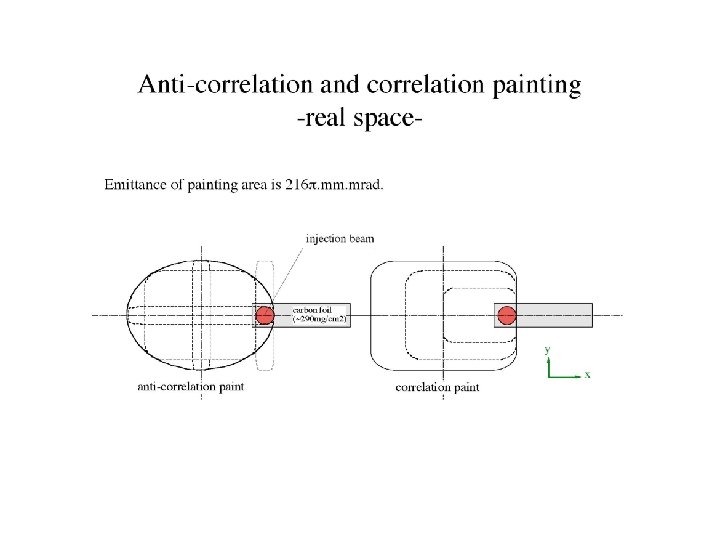
Schematic Layout of Beam Orbit at Painting Injection Start

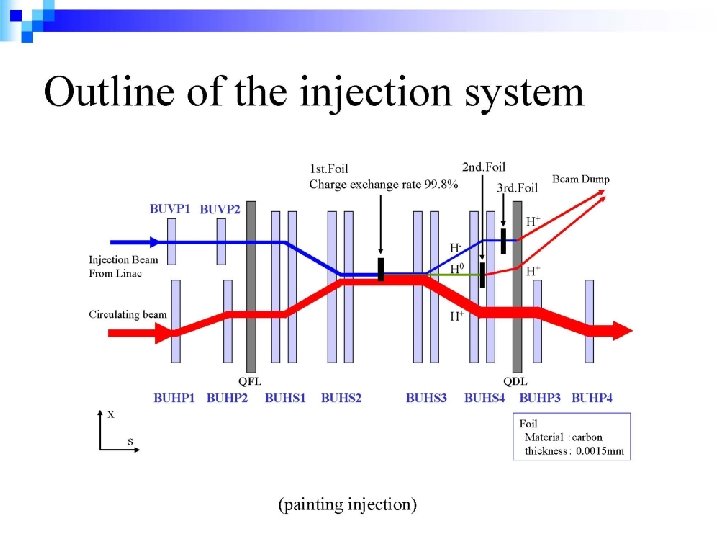
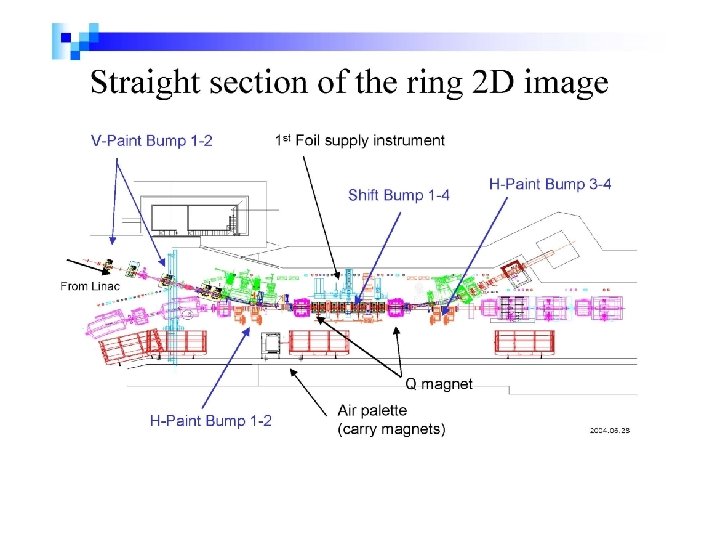
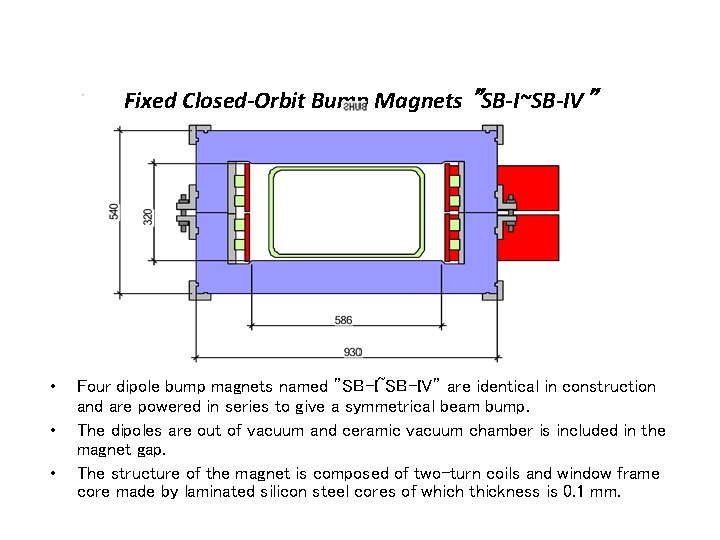
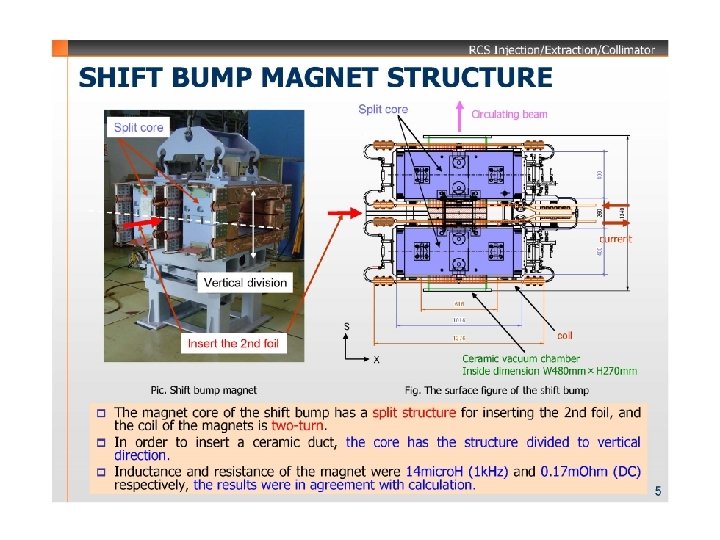
Fixed Closed-Orbit Bump Magnets ”SB-I~SB-IV” • • • Four dipole bump magnets named ”SB-I~SB-IV” are identical in construction and are powered in series to give a symmetrical beam bump. The dipoles are out of vacuum and ceramic vacuum chamber is included in the magnet gap. The structure of the magnet is composed of two-turn coils and window frame core made by laminated silicon steel cores of which thickness is 0. 1 mm.

Structure of the Split-type Bump Magnet • The exitation current is supplied in the middle of the core trough the split to form a symmetrical distribution of magnetic field along the longitudinal direction. • To insert the second foil • Symmetrical power supply for a symmetrical field distribution along the longitudinal axis

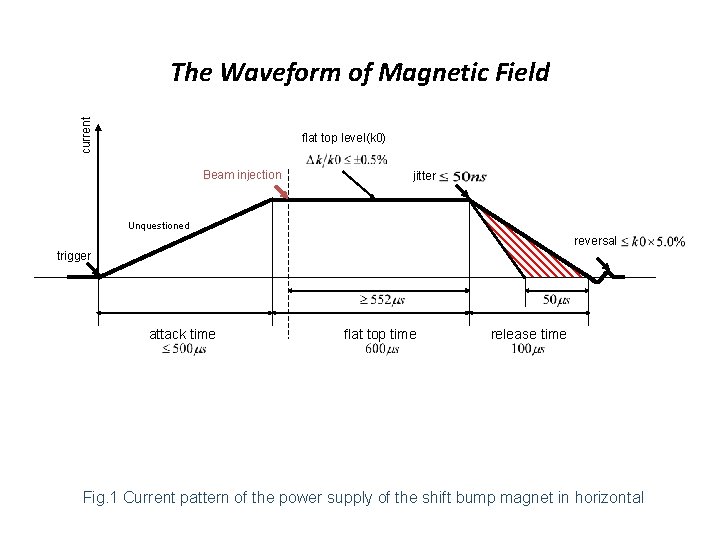
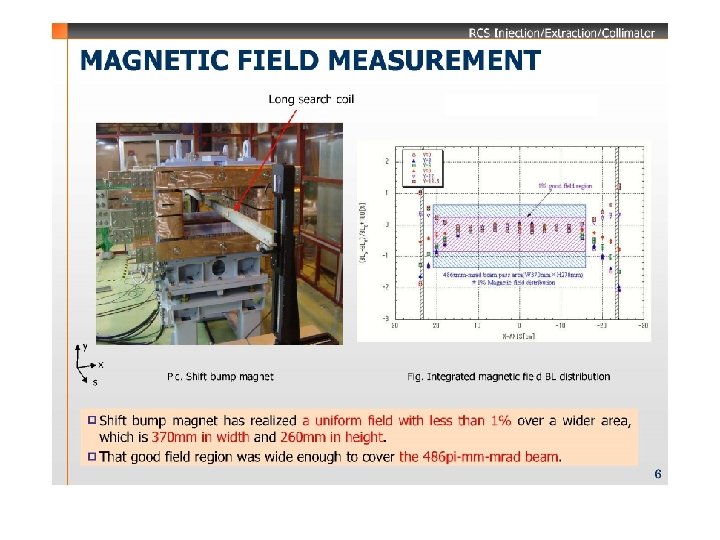
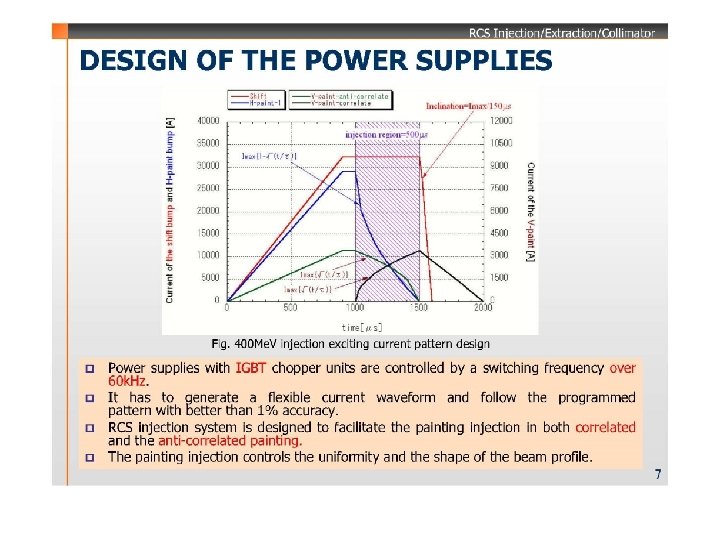
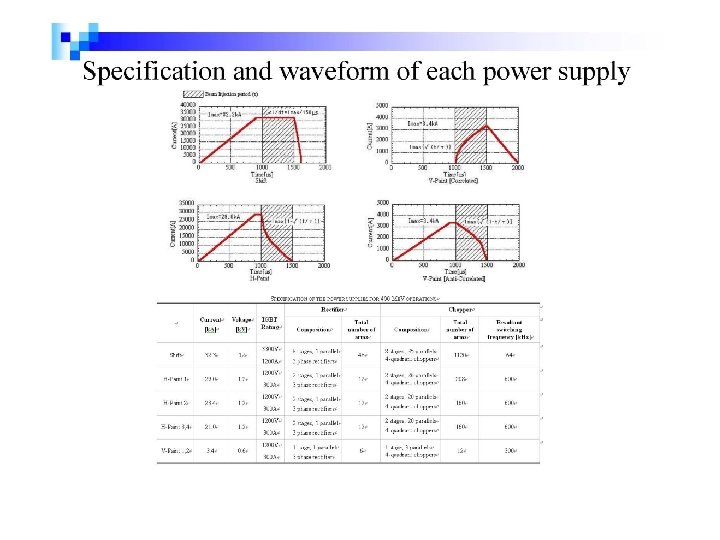
current The Waveform of Magnetic Field flat top level(k 0) Beam injection jitter Unquestioned reversal trigger attack time flat top time release time Fig. 1 Current pattern of the power supply of the shift bump magnet in horizontal

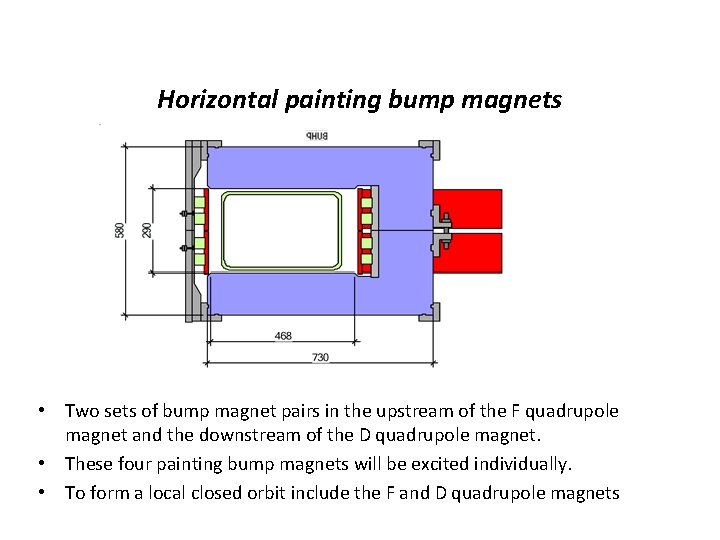
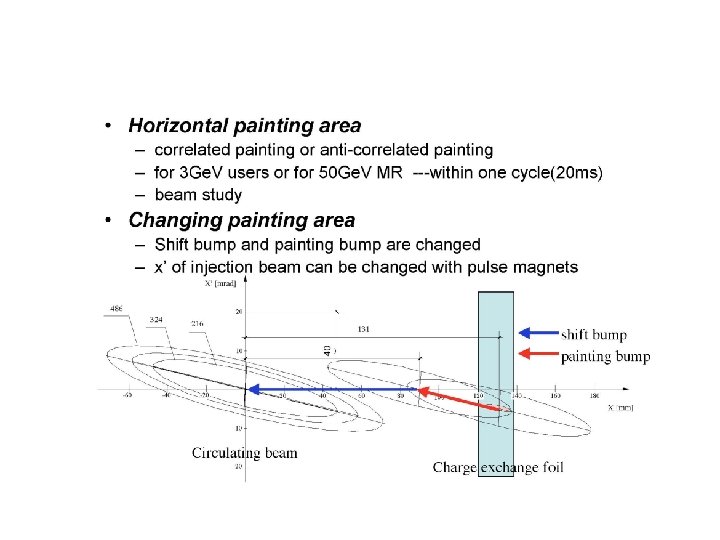
Horizontal painting bump magnets • Two sets of bump magnet pairs in the upstream of the F quadrupole magnet and the downstream of the D quadrupole magnet. • These four painting bump magnets will be excited individually. • To form a local closed orbit include the F and D quadrupole magnets

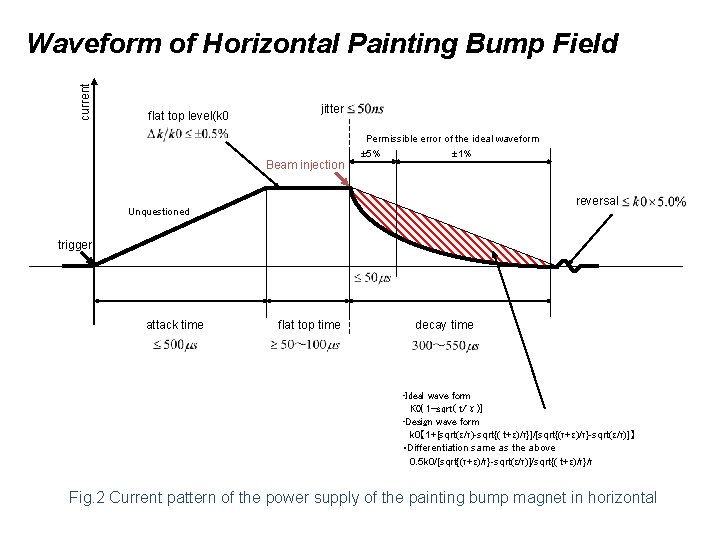
current Waveform of Horizontal Painting Bump Field flat top level(k 0 jitter Permissible error of the ideal waveform Beam injection ± 5% ± 1% reversal Unquestioned trigger attack time flat top time decay time • Ideal wave form K 0{ 1 -sqrt( t/τ)} • Design wave form k 0【 1+[sqrt(ε/τ)-sqrt{( t+ε)/τ}]/[sqrt{(τ+ε)/τ}-sqrt(ε/τ)]】 • Differentiation same as the above 0. 5 k 0/[sqrt{(τ+ε)/τ}-sqrt(ε/τ)]/sqrt{( t+ε)/τ}/τ Fig. 2 Current pattern of the power supply of the painting bump magnet in horizontal

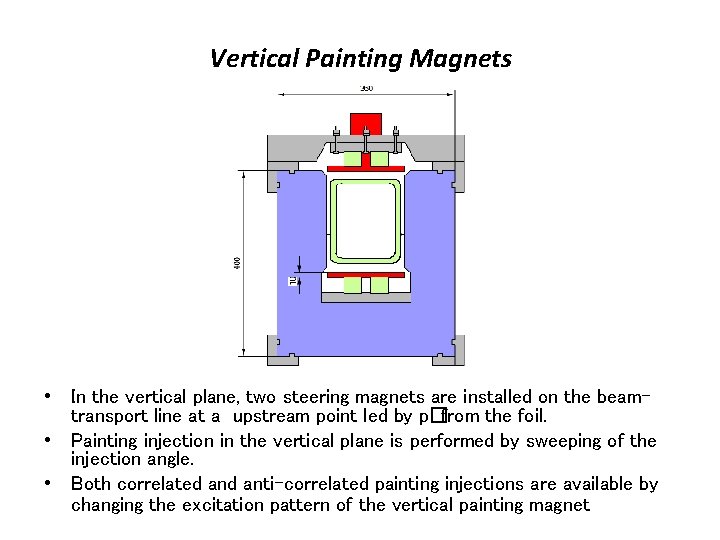
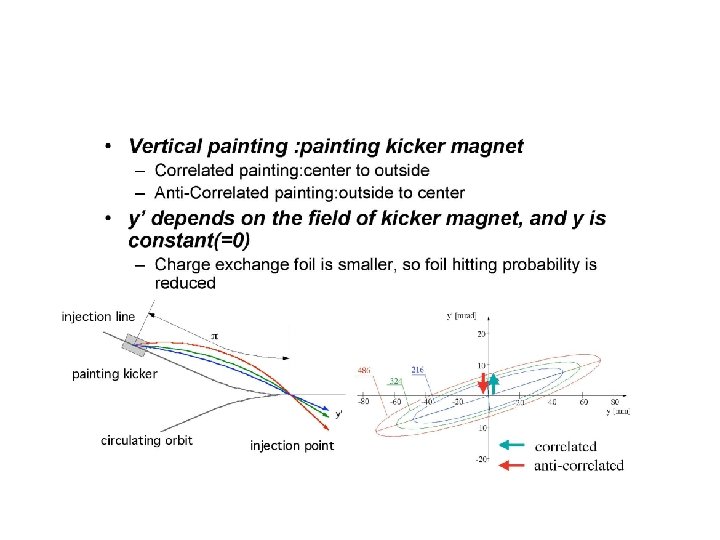
Vertical Painting Magnets • In the vertical plane, two steering magnets are installed on the beamtransport line at a upstream point led by p�from the foil. • Painting injection in the vertical plane is performed by sweeping of the injection angle. • Both correlated anti-correlated painting injections are available by changing the excitation pattern of the vertical painting magnet

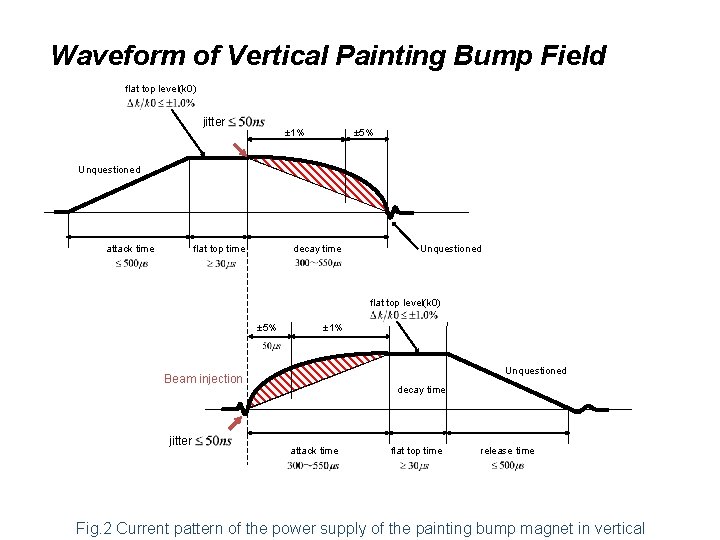
Waveform of Vertical Painting Bump Field flat top level(k 0) jitter ± 1% ± 5% Unquestioned attack time flat top time decay time Unquestioned flat top level(k 0) ± 5% ± 1% Unquestioned Beam injection jitter decay time attack time flat top time release time Fig. 2 Current pattern of the power supply of the painting bump magnet in vertical