Fast lidar radar multiplescattering models for cloud retrievals

Fast lidar & radar multiple-scattering models for cloud retrievals Robin Hogan (University of Reading) Alessandro Battaglia (University of Bonn) • How can we account for radar and lidar multiple scattering in Cloud. Sat/Calipso/Earth. CARE retrievals? • Overview of talk: – – Examples of multiple scattering from Cloud. Sat and LITE “Variational” retrievals and forward modelling of radar/lidar signals The four scattering regimes Fast modelling of “quasi-small-angle” multiple scattering using the photon variance-covariance method – Fast modelling of “wide-angle” multiple scattering using the timedependent two-stream approximation – Comparison with Monte-Carlo calculations for radar and lidar

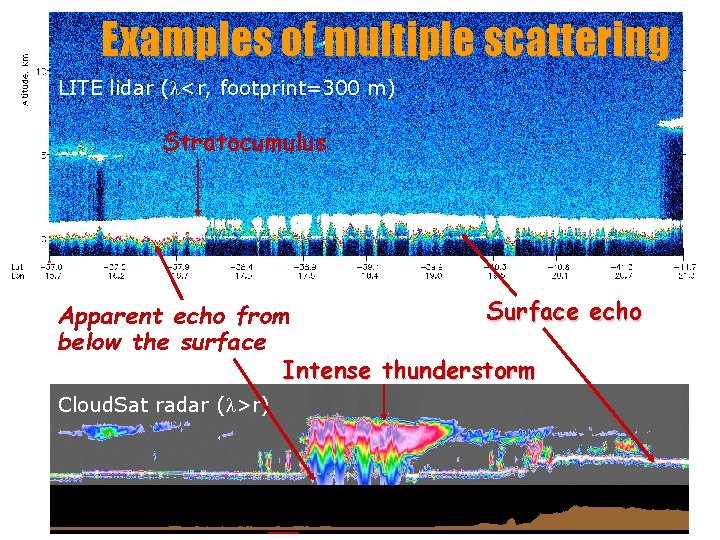
Examples of multiple scattering • LITE lidar (l<r, footprint=300 m) Stratocumulus Surface echo Apparent echo from below the surface Intense thunderstorm Cloud. Sat radar (l>r)

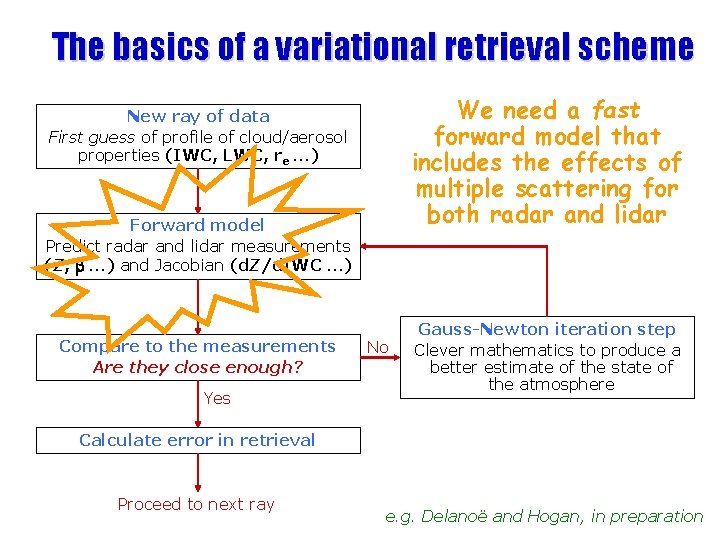
The basics of a variational retrieval scheme We need a fast forward model that includes the effects of multiple scattering for both radar and lidar New ray of data First guess of profile of cloud/aerosol properties (IWC, LWC, re …) Forward model Predict radar and lidar measurements (Z, b …) and Jacobian (d. Z/d. IWC …) Compare to the measurements Are they close enough? Yes No Gauss-Newton iteration step Clever mathematics to produce a better estimate of the state of the atmosphere Calculate error in retrieval Proceed to next ray e. g. Delanoë and Hogan, in preparation

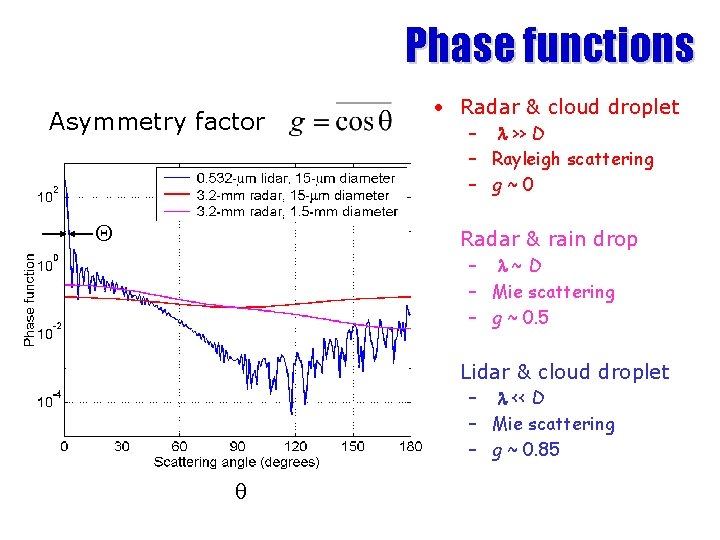
Phase functions Asymmetry factor Q • Radar & cloud droplet – l >> D – Rayleigh scattering – g~0 • Radar & rain drop – l~D – Mie scattering – g ~ 0. 5 • Lidar & cloud droplet – l << D – Mie scattering – g ~ 0. 85 q

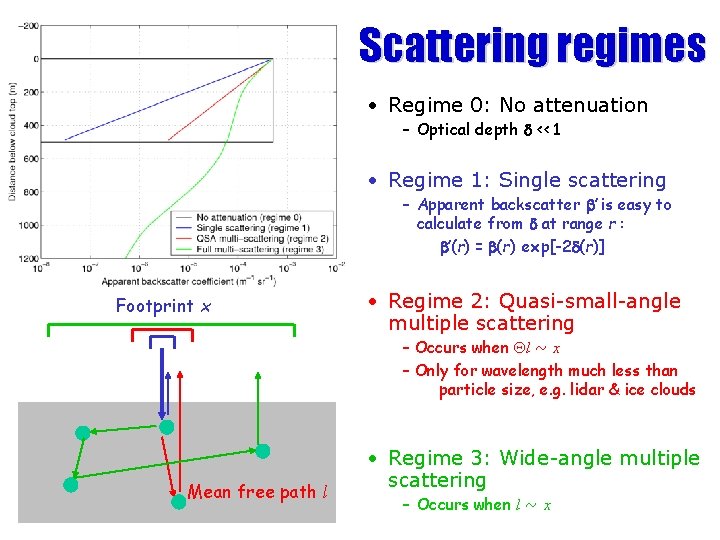
Scattering regimes • Regime 0: No attenuation – Optical depth d << 1 • Regime 1: Single scattering – Apparent backscatter b’ is easy to calculate from d at range r : b’(r) = b(r) exp[-2 d(r)] Footprint x • Regime 2: Quasi-small-angle multiple scattering – Occurs when Ql ~ x – Only for wavelength much less than particle size, e. g. lidar & ice clouds Mean free path l • Regime 3: Wide-angle multiple scattering – Occurs when l ~ x

New radar/lidar forward model • Cloud. Sat/Calipso record a new profile every 0. 1 s – An “operational” forward model clearly must run in much less than 0. 01 s! • Most widely used existing methods: – Regime 2: Eloranta (1998) – too slow – Regime 3: Monte Carlo – much too slow! • Two fast new methods: – Regime 2: Photon Variance-Covariance (PVC) method – Regime 3: Time-Dependent Two-Stream (TDTS) method • Sum the signal from the relevant methods: – Radar: regime 1 (single scattering) plus regime 3 – Lidar: regime 2 plus regime 3

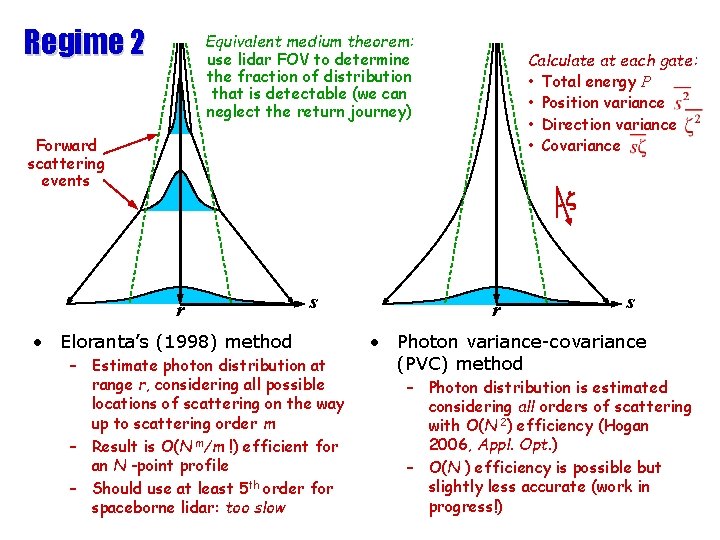
Regime 2 Equivalent medium theorem: use lidar FOV to determine the fraction of distribution that is detectable (we can neglect the return journey) Calculate at each gate: • Total energy P • Position variance • Direction variance • Covariance Forward scattering events z r s • Eloranta’s (1998) method – Estimate photon distribution at range r, considering all possible locations of scattering on the way up to scattering order m – Result is O(N m/m !) efficient for an N -point profile – Should use at least 5 th order for spaceborne lidar: too slow r s • Photon variance-covariance (PVC) method – Photon distribution is estimated considering all orders of scattering with O(N 2) efficiency (Hogan 2006, Appl. Opt. ) – O(N ) efficiency is possible but slightly less accurate (work in progress!)

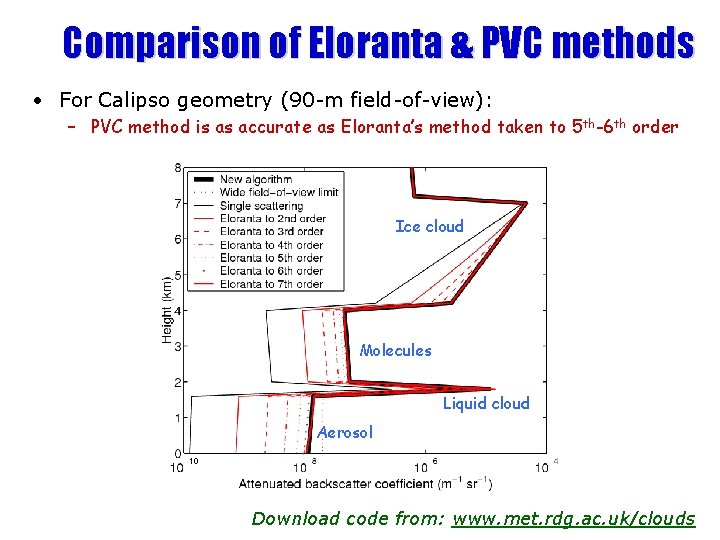
Comparison of Eloranta & PVC methods • For Calipso geometry (90 -m field-of-view): – PVC method is as accurate as Eloranta’s method taken to 5 th-6 th order Ice cloud Molecules Liquid cloud Aerosol Download code from: www. met. rdg. ac. uk/clouds

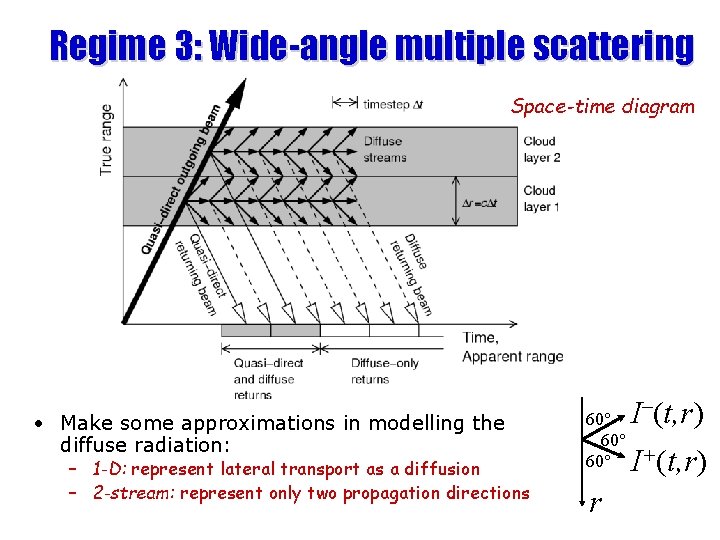
Regime 3: Wide-angle multiple scattering Space-time diagram • Make some approximations in modelling the diffuse radiation: – 1 -D: represent lateral transport as a diffusion – 2 -stream: represent only two propagation directions I–(t, r) 60° + 60° I (t, r) r

Time-dependent 2 -stream approx. • Describe diffuse flux in terms of outgoing stream I+ and incoming stream I–, and numerically integrate the following coupled PDEs: Source Time derivative Scattering from the quasi-direct beam into each of the streams Remove this and we have the timeindependent twostream approximation used in weather models Gain by scattering Spatial derivative A bit like an advection term, representing how much radiation is upstream Loss by absorption or scattering Some of lost radiation will enter the other stream Radiation scattered from the other stream • These can be discretized quite simply in time and space (no implicit methods or matrix inversion required)

Lateral photon spreading • Model the lateral variance of photon position, following equations (where ): , using the Additional source Increasing variance with time is described by a diffusivity D • Then assume the lateral photon distribution is Gaussian to predict what fraction of it lies within the field-of-view • Resulting method is O(N 2) efficient

Simulation of 3 D photon transport • Animation of scalar flux (I++I –) – Colour scale is logarithmic – Represents 5 orders of magnitude • Domain properties: – – 500 -m thick 2 -km wide Optical depth of 20 No absorption • In this simulation the lateral distribution is Gaussian at each height and each time

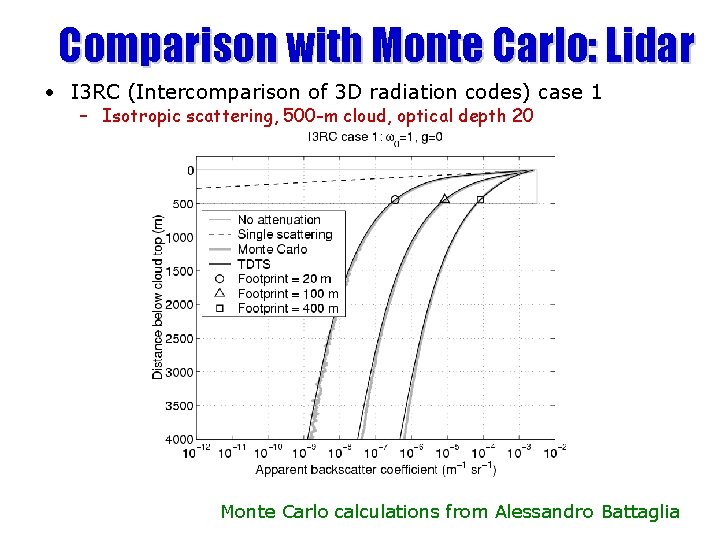
Comparison with Monte Carlo: Lidar • I 3 RC (Intercomparison of 3 D radiation codes) case 1 – Isotropic scattering, 500 -m cloud, optical depth 20 Monte Carlo calculations from Alessandro Battaglia

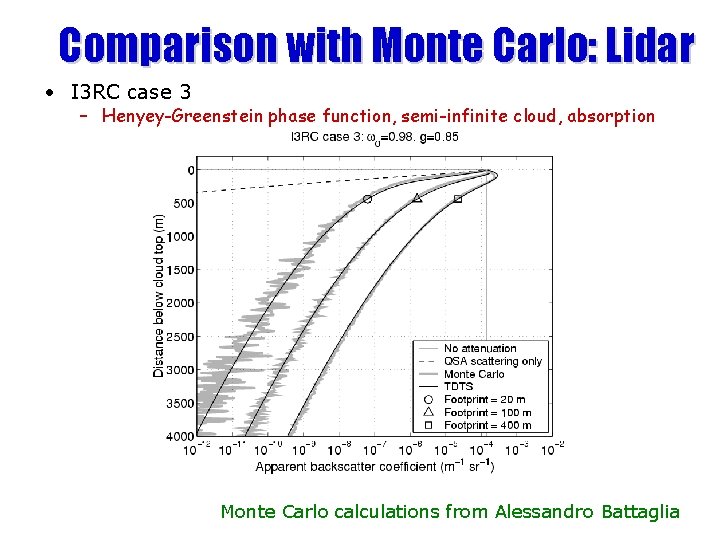
Comparison with Monte Carlo: Lidar • I 3 RC case 3 – Henyey-Greenstein phase function, semi-infinite cloud, absorption Monte Carlo calculations from Alessandro Battaglia

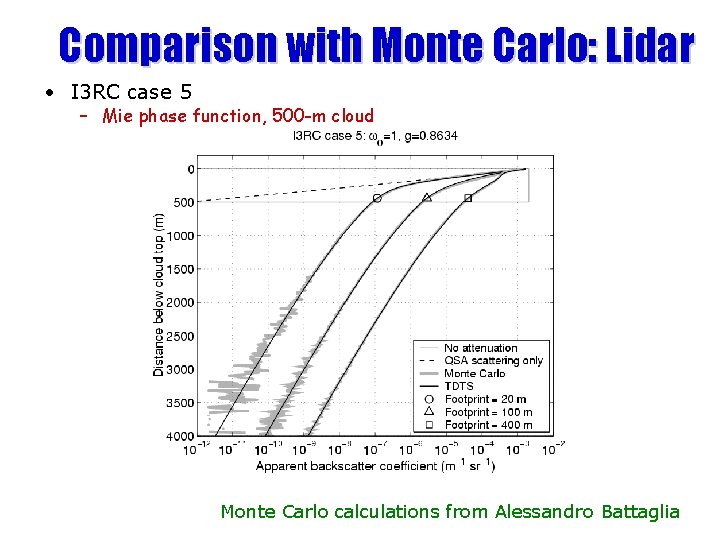
Comparison with Monte Carlo: Lidar • I 3 RC case 5 – Mie phase function, 500 -m cloud Monte Carlo calculations from Alessandro Battaglia

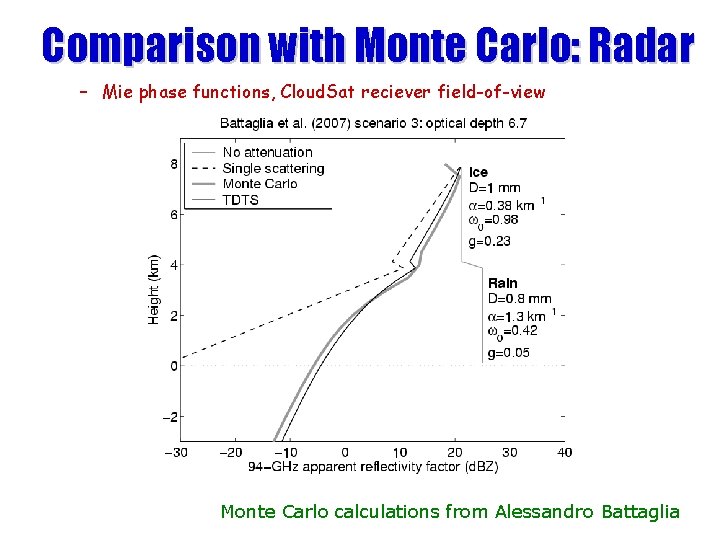
Comparison with Monte Carlo: Radar – Mie phase functions, Cloud. Sat reciever field-of-view Monte Carlo calculations from Alessandro Battaglia

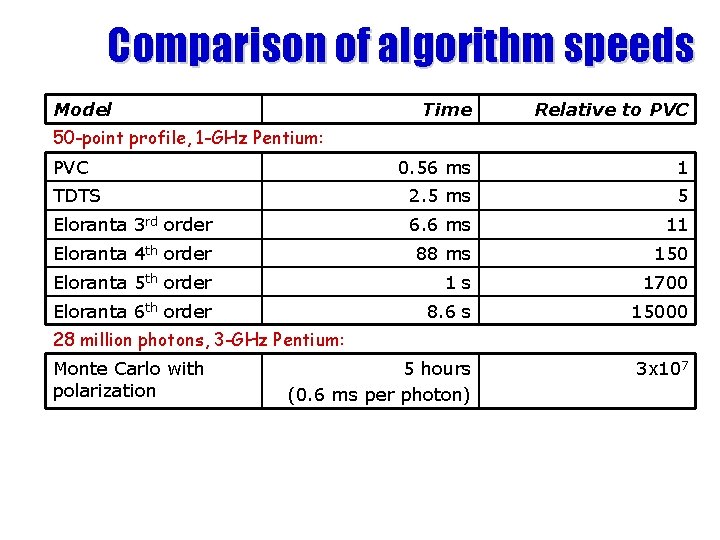
Comparison of algorithm speeds Model Time Relative to PVC 0. 56 ms 1 TDTS 2. 5 ms 5 Eloranta 3 rd order 6. 6 ms 11 Eloranta 4 th order 88 ms 150 Eloranta 5 th order 1 s 1700 Eloranta 6 th order 8. 6 s 15000 5 hours (0. 6 ms per photon) 3 x 107 50 -point profile, 1 -GHz Pentium: PVC 28 million photons, 3 -GHz Pentium: Monte Carlo with polarization

Future work • Implement TDTS in Cloud. Sat/Calipso retrieval (PVC is already implemented for lidar) – More confidence in lidar retrievals of liquid water clouds – Can interpret Cloud. Sat returns in deep convection – But need to find a fast way to estimate the Jacobian of TDTS • Add the capability to have a partially reflecting surface • Apply to multiple field-of-view lidars – The difference in backscatter for two different fields of view enables the multiple scattering to be interpreted in terms of cloud properties • Predict the polarization of the returned signal – Difficult but useful for both radar and lidar • It would be simple to predict the HSRL channel of Earth. CARE

Interpretation of radar and lidar • We want to know the profile of the important cloud properties: – Liquid or ice water content (g m-3) – The mean size of the droplets or ice particles – In principle these properties can be derived utilizing the very different scattering mechanisms of radar and lidar • We have developed a variational algorithm to interpret the combined measurements (“ 1 D-Var” in data assimilation): – – Make a first guess of the cloud profile Use forward models to simulate the corresponding observations Compare the forward model values with the actual observations Use Gauss-Newton iteration to refine the cloud profile to achived a better fit with the observations in a least-squares sense • We need accurate radar and lidar forward models, but multiple scattering can make life difficult!

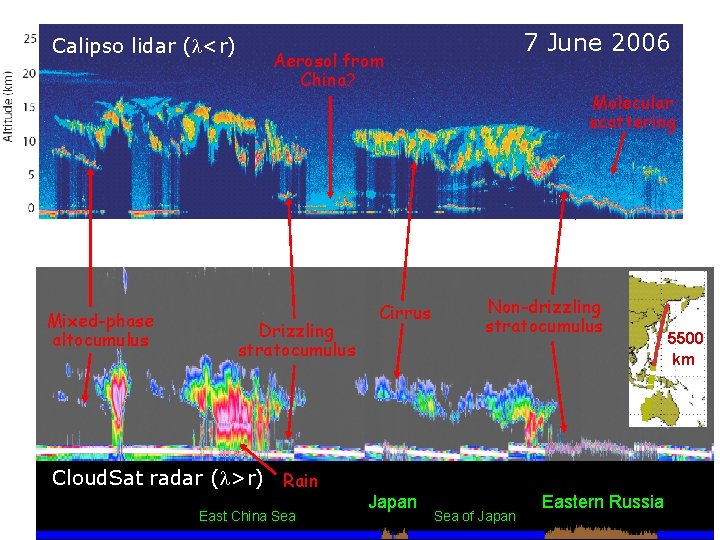
• Calipso lidar (l<r) Mixed-phase altocumulus 7 June 2006 Aerosol from China? Drizzling stratocumulus • Cloud. Sat radar (l>r) Rain East China Sea Cirrus Japan Molecular scattering Non-drizzling stratocumulus Sea of Japan Eastern Russia 5500 km

The 3 D radiative transfer equation • Also known as the “Boltzmann transport equation”, this describes the evolution of the radiative intensity I as a function of time t, position x and direction W: Loss by absorption Time derivative or scattering Gain by scattering Spatial derivative Radiation scattered from representing how much radiation is upstream Source all other directions • Can use Monte Carlo but very expensive • Must make some approximations: – 1 -D: represent lateral transport as a diffusion – 2 -stream: represent only two propagation directions I–(t, r) 60° + 60° I (t, r) r