Fast Inverse Square Root Anubhav Srivastava 4 A

Fast Inverse Square Root Anubhav Srivastava, 4 A CS

Overview 1. Motivation 2. A look at the code ○ *confusion* 3. Explanation of the core step (minus the hard part) 4. Newton’s method 5. The hard part (brief!) 6. Recap 7. Questions
Motivation

Motivation ● 1
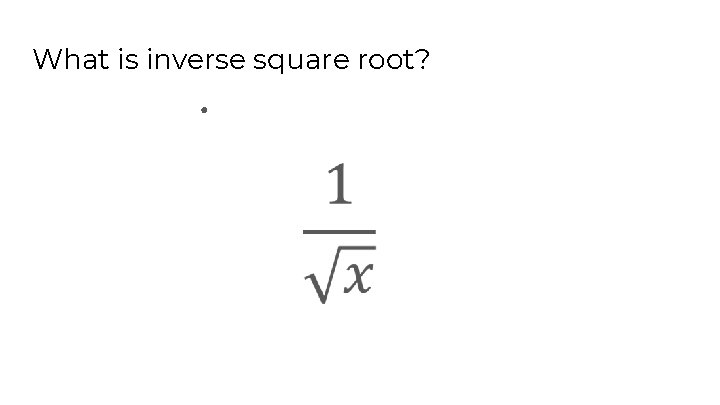
What is inverse square root? ●

A look at the code

A look at the code

A look at the code

Floating point representation ● 1 0 0 0 1 0 0 0 0 0

Floating point representation ● 1 0 0 0 1 0 0 0 0 0

A look at the code

A look at the code

A look at the code
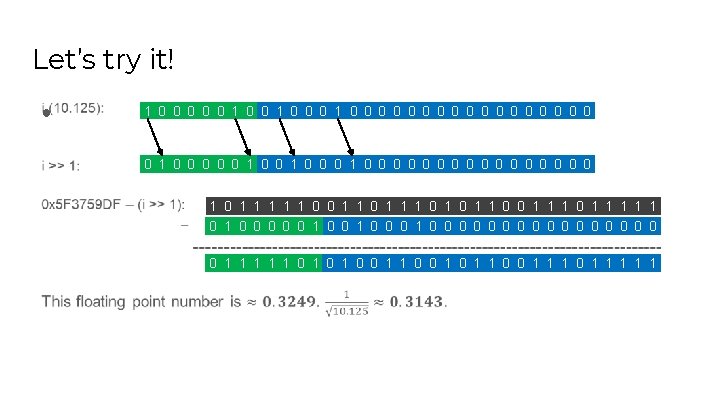
Let’s try it! ● 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 0 0 0 1 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 1 1 1 1 1

What’s going on? ●

What’s going on (exponent)? ● 1 0 1 1 1 0 ? ? ? ? i >> 1 Subtract from 0 x 5 F

A look at the code (again)

Improving our guess
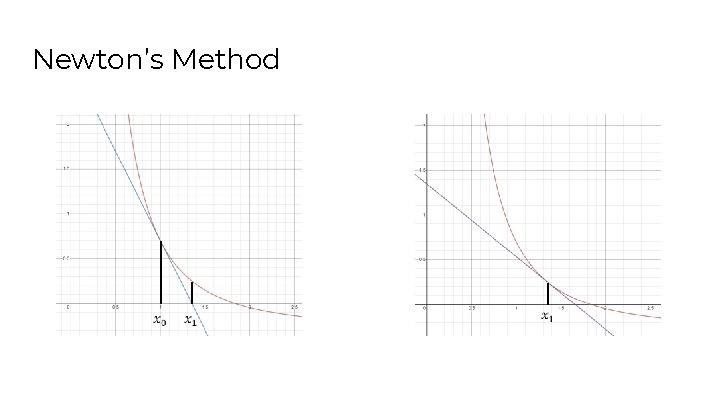
Newton’s Method
Newton’s Method
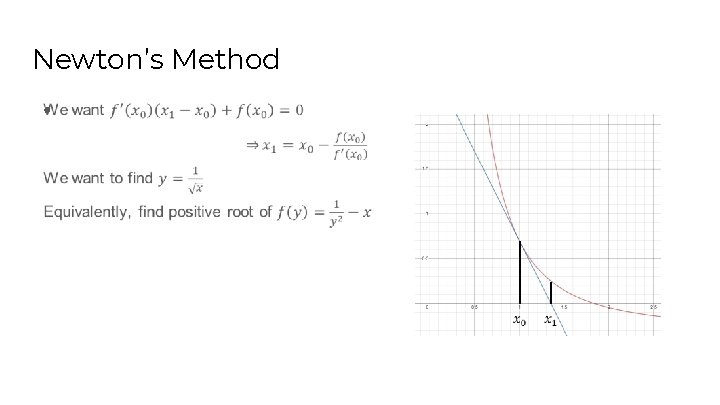
Newton’s Method ●

Newton’s Method ●

Done!

Done!

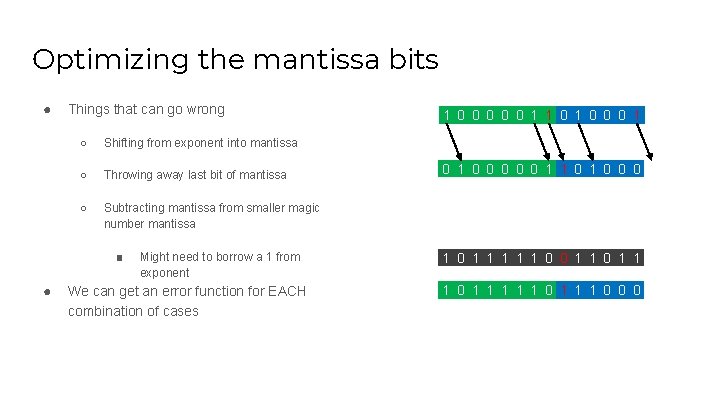
Optimizing the mantissa bits ● Things that can go wrong ○ Shifting from exponent into mantissa ○ Throwing away last bit of mantissa ○ Subtracting mantissa from smaller magic number mantissa ■ ● Might need to borrow a 1 from exponent We can get an error function for EACH combination of cases 1 0 0 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 0 1 1 1 0 0 0

Optimizing the mantissa bits
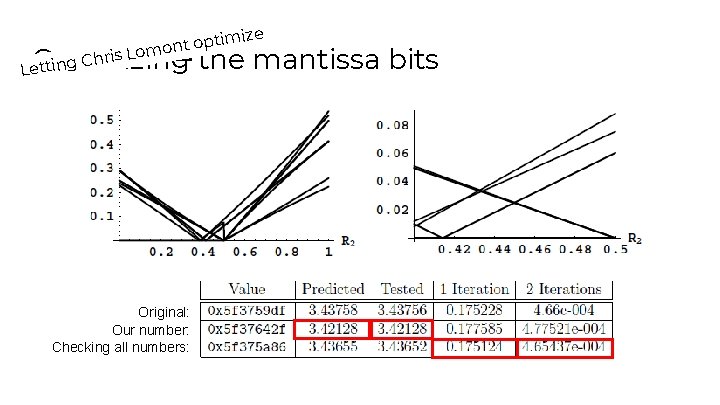
mize i t p o t Lomon s i r h C g Optimizing the mantissa bits Lettin Original: Our number: Checking all numbers:

Recap ●
Questions?

Sources Main source Chris Lomont: “Fast Inverse Square Root” https: //www. lomont. org/papers/2003/Inv. Sqrt. pdf Other papers: Charles Mc. Eniry: "The Mathematics Behind the Fast Inverse Square Root Function Code" https: //web. archive. org/web/20150511044204/http: //www. daxia. com/bibis/upload/406 Fast_Inverse_Square_Root. pdf Leonid Moroz (et al. ): “Fast calculation of inverse square root with the use of magic constant − analytical approach” https: //arxiv. org/abs/1603. 04483
- Slides: 31