Fast Fourier Transform A bunch of smart people

Outline (hopefully) • • • Finite discrete signals Linear shift-invariant filters Impulse responses Circular convolutions Discrete Fourier Transform The Fast Fourier Transform

Continuous signals

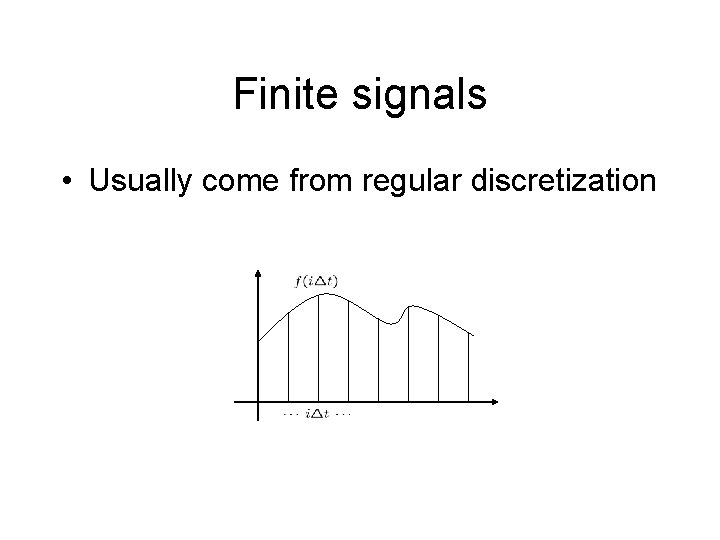
Finite signals • Usually come from regular discretization

Finite signals • Usually come from regular discretization • Might as well think of them as vectors!

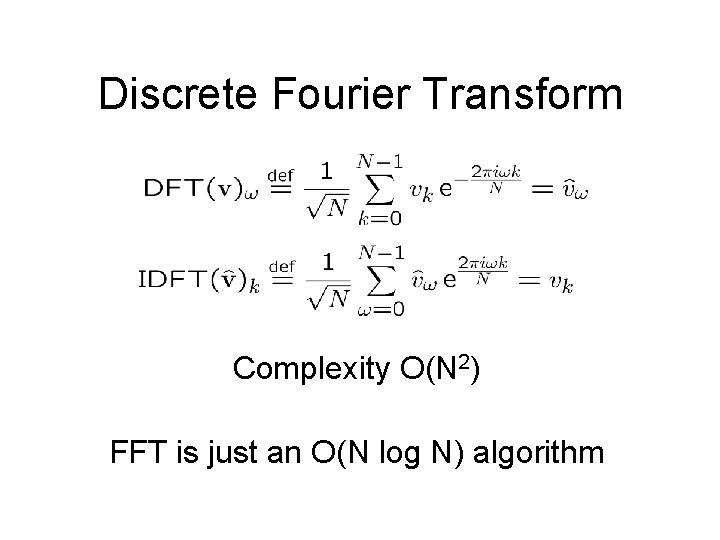
Discrete Fourier Transform Complexity O(N 2) FFT is just an O(N log N) algorithm

Transformations on vectors Linear (i. e. , matrices)

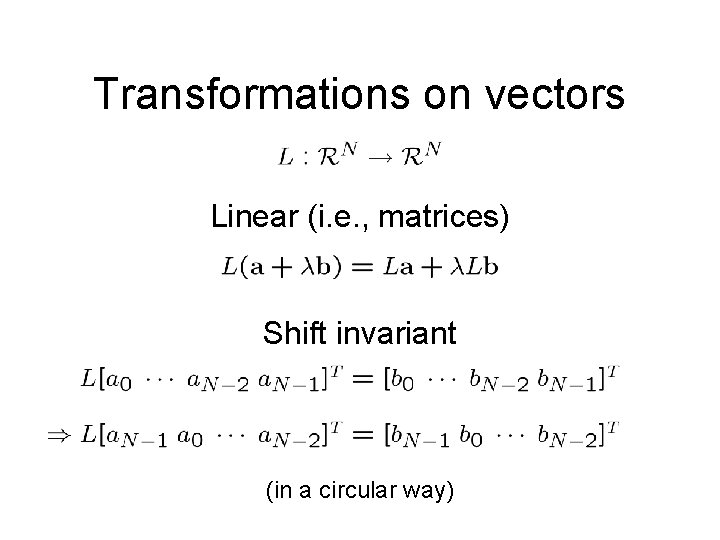
Transformations on vectors Linear (i. e. , matrices) Shift invariant (in a circular way)

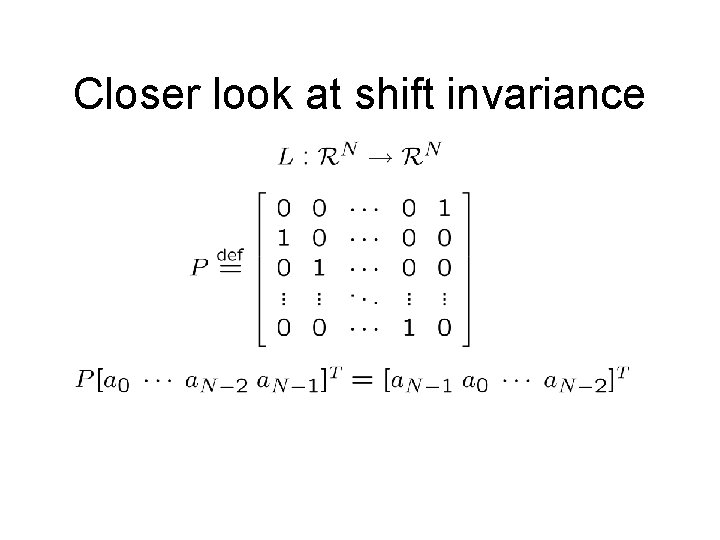
Closer look at shift invariance

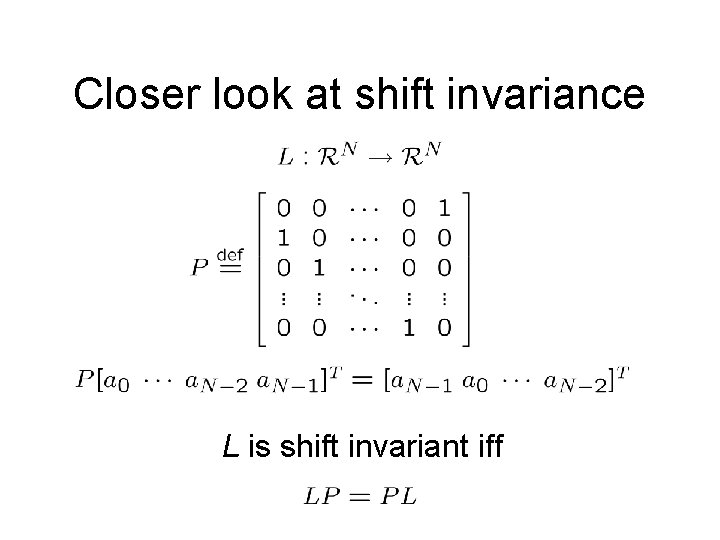
Closer look at shift invariance L is shift invariant iff

The canonic basis of RN is the canonic basis for plays the role of Dirac's delta or impulse

How does matrix L look like? h is the impulse response of L It captures all information about L!

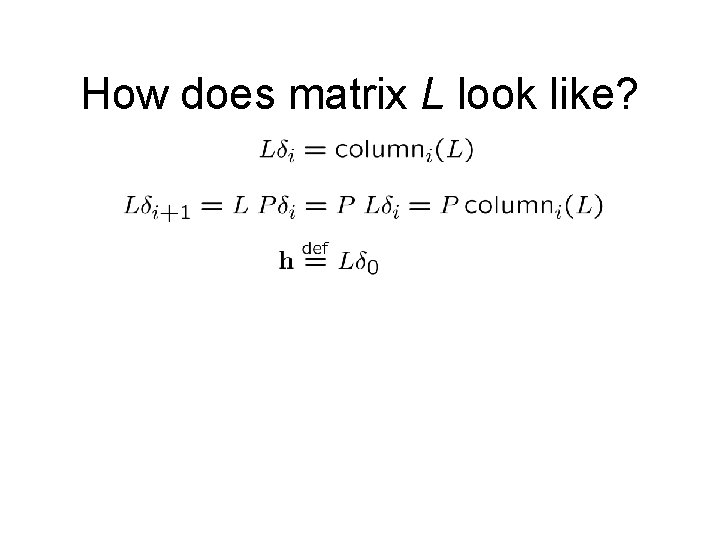
How does matrix L look like?

How do we multiply L by v? This is why we care about convolutions!

The circular convolution Complexity O(N 2)

What we have so far • We discretized a continuous function turning it into a vector in RN • We defined a class of transformations from RN to RN that we care about • Each linear shift-invariant transformations L can be written as a circular convolution • The convolution is with the impulse response h of the transformation L • We can compute it in O(N 2)

This is too abstract! • Want to make a recording of your voice sound as if you were inside a bathroom? • Your bathroom transform sound in a linear, shift invariant way. • Record the sound of a clap in the bathroom. • Record your voice outside. • Convolve the two signals!

Easy to do in Matlab a = wavread('bathroom-ip. wav'); b = wavread('laugh. wav'); a = a / max(abs(a)); b = b / max(abs(b)); c = conv(a, b); c = c / max(abs(c)); p = audioplayer(c, 44000); play(p, [1 length(c)])

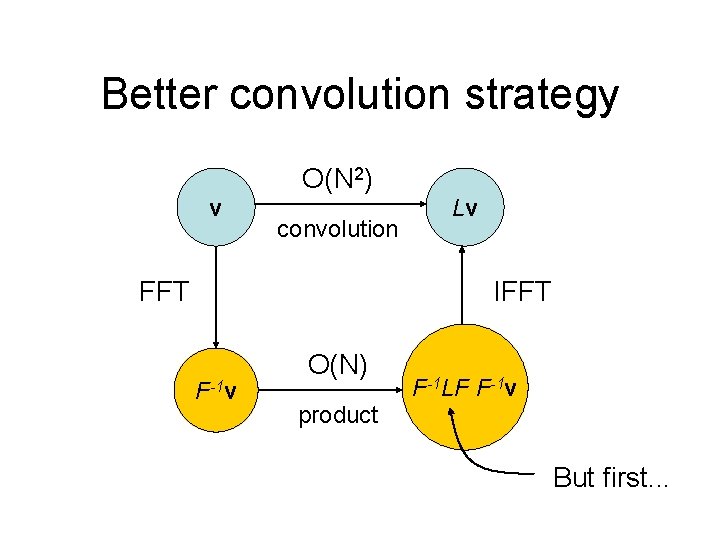
Better convolution strategy O(N 2) v convolution FFT Lv IFFT F-1 v O(N) F-1 LF F-1 v product But first. . .

Diagonalizing L • Need a basis of eigenvectors for L. Trick is to look at P first! • Assume for now that P has distinct eigenvalues. • If wi is an eigenvector of P, then it is also an eigenvector of L! • Lwi is an eigenvector of P, with the same eigenvalue • We must have • wi is also eigenvector of L (for some other eigenvalue) • Since P has a full set of wi, L is diagonalized by the same wi!

The eigenvalues of P Indeed, P has a full set!

The eigenvectors wk of P

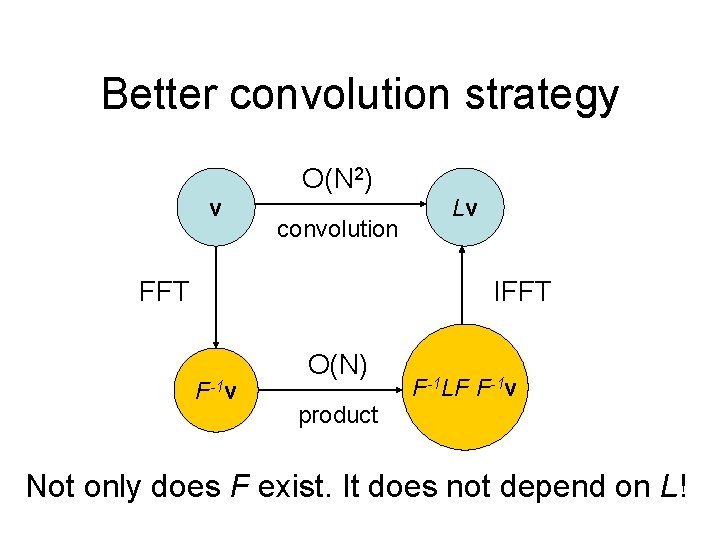
Better convolution strategy O(N 2) v convolution FFT Lv IFFT F-1 v O(N) F-1 LF F-1 v product Not only does F exist. It does not depend on L!

How do F and F-1 look like? We can also verify that. . .

How to compute F-1 v? Finally!!!

The eigenvalues of L Finally!!!

Discrete Fourier Transform FFT is just an O(N log N) algorithm

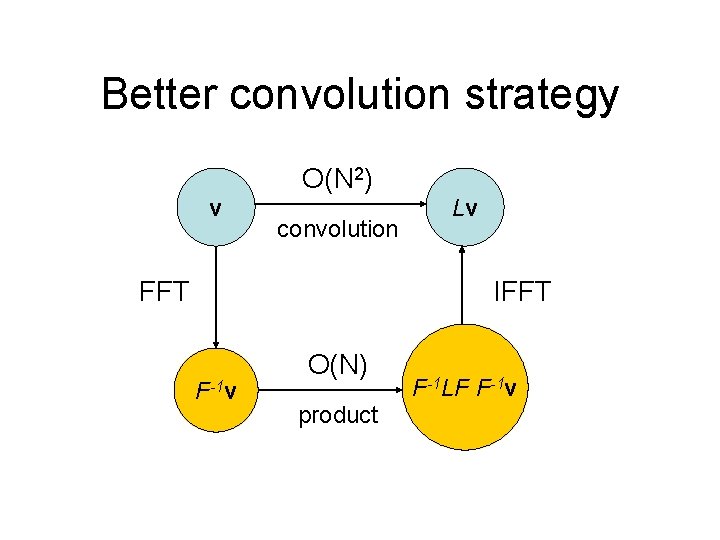
Better convolution strategy O(N 2) v convolution FFT Lv IFFT F-1 v O(N) product F-1 LF F-1 v

Fast Fourier Transform

Fast Fourier Transform • Coley and Tukey, 1965 • Gauss, 1805

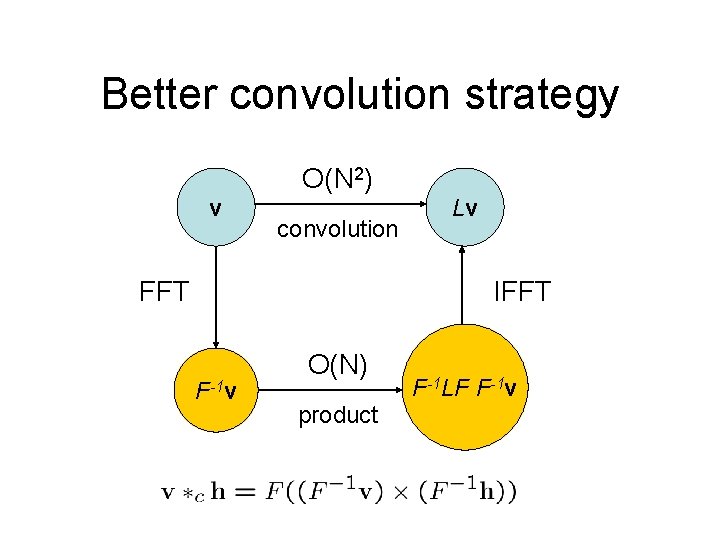
Better convolution strategy O(N 2) v convolution FFT Lv IFFT F-1 v O(N) product F-1 LF F-1 v

Easy to do in Matlab a = wavread('bathroom-ip. wav'); b = wavread('laugh. wav'); a = a / max(abs(a)); b = b / max(abs(b)); c = fftfilt(a, b); c = c / max(abs(c)); p = audioplayer(c, 44000); play(p, [1 length(c)])