Fast Factorized BackProjection FFBP EECS 826 SAR INVESTIGATION

Fast Factorized Back-Projection (FFBP) EECS 826 SAR INVESTIGATION 22 APRIL 2021 1

Intro Review Back Projection Factorization Conclusion Credits • Introduction • Review – SAR image forming algorithms • Back Projection – Geometry + echo model • Factorization – concept only illustrations and equations taken from the reference • Conclusion • Credits – References 2

Intro Review Back Projection Factorization Conclusion Credits SAR processing algorithms (a few) • Why do we use them? Signal Image • How do they work? Time &/ Frequency domain operations in Range &/ Azimuth dimensions • What do they do? Range compression (RC), Range cell migration correction (RCMC), Azimuth compression (AC) 3

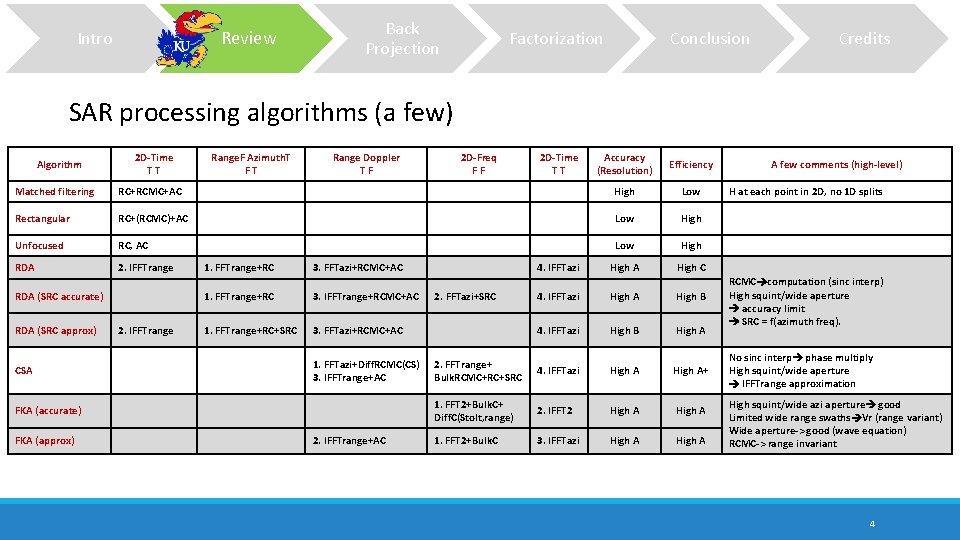
Review Intro Back Projection Factorization Conclusion Credits SAR processing algorithms (a few) Algorithm 2 D-Time TT Range. F Azimuth. T FT Range Doppler TF 2 D-Freq FF 2 D-Time TT Accuracy (Resolution) Efficiency Matched filtering RC+RCMC+AC High Low Rectangular RC+(RCMC)+AC Low High Unfocused RC, AC Low High RDA 2. IFFTrange 4. IFFTazi High A High C 4. IFFTazi High A High B 4. IFFTazi High B High A 2. FFTrange+ Bulk. RCMC+RC+SRC 4. IFFTazi High A+ 1. FFT 2+Bulk. C+ Diff. C(Stolt, range) 2. IFFT 2 High A 1. FFT 2+Bulk. C 3. IFFTazi High A RDA (SRC accurate) RDA (SRC approx) CSA 2. IFFTrange 1. FFTrange+RC 3. FFTazi+RCMC+AC 1. FFTrange+RC 3. IFFTrange+RCMC+AC 1. FFTrange+RC+SRC 3. FFTazi+RCMC+AC 1. FFTazi+Diff. RCMC(CS) 3. IFFTrange+AC FKA (accurate) FKA (approx) 2. IFFTrange+AC 2. FFTazi+SRC A few comments (high-level) H at each point in 2 D, no 1 D splits RCMC computation (sinc interp) High squint/wide aperture accuracy limit SRC = f(azimuth freq). No sinc interp phase multiply High squint/wide aperture IFFTrange approximation High squint/wide azi aperture good Limited wide range swaths Vr (range variant) Wide aperture-> good (wave equation) RCMC-> range invariant 4

Review Intro Back Projection Factorization Conclusion Credits SAR processing algorithms (a few) Lets go back in time… Ealry works 1950 s 1960 s Polar. Format (PFA) (Motion. Through. Resolution. Cell) 1970 s RDA 1976 -78 Inversion methods like Fourier. Hankel and Range-Migration (FKA) 1987 CSA 1993 FFBP 2003 Optical, time domain Freq domain linear aperture Non-linear cases tiles for local motion correction Large memory + 2 D freq transforms Time domain zero padding for Stolt interp A solution for a general geometry: 2 D-Time domain image formation, Back projecting 5

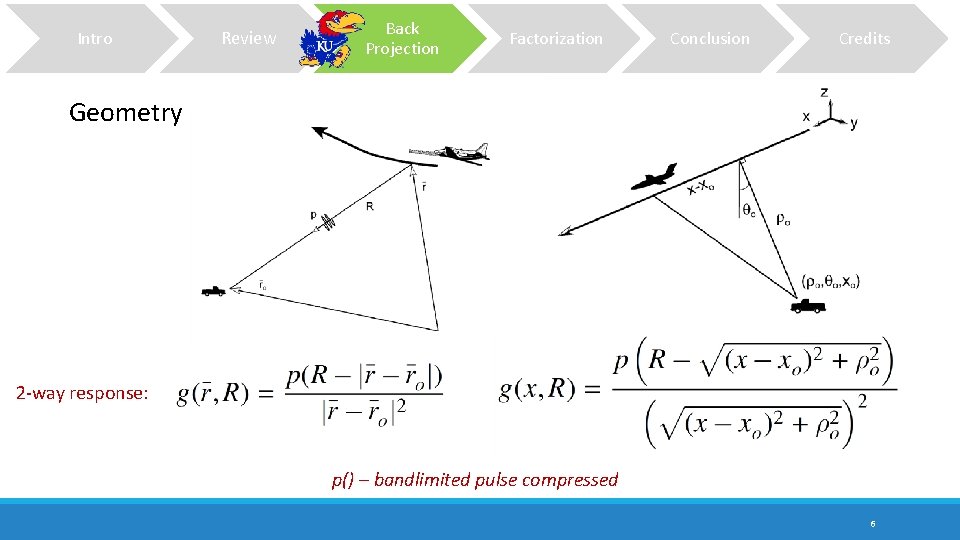
Intro Review Back Projection Factorization Conclusion Credits Geometry 2 -way response: p() – bandlimited pulse compressed 6

Review Intro Back Projection Factorization Conclusion Credits Echo model Back projected signal for a position (x, ρ): [Pixels in a map] Back projected signal for a non-linear track: [arbitrary position] Baseband representation: *** For an L-length track to map M x N size image: computations = constant * ( L * M * N ) Smaller images are fine, but large ones ? ? 7

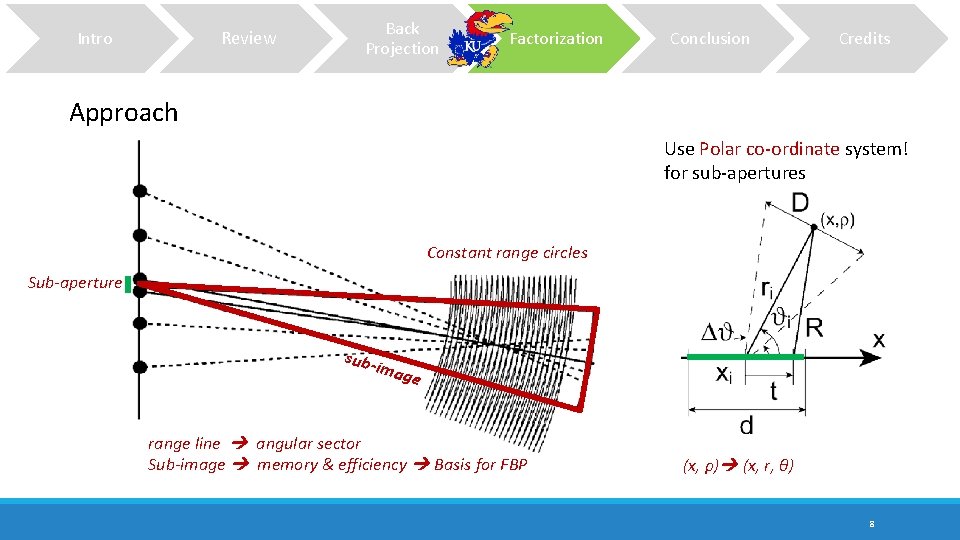
Review Intro Back Projection Factorization Conclusion Credits Approach Use Polar co-ordinate system! for sub-apertures Constant range circles Sub-aperture subim age range line angular sector Sub-image memory & efficiency Basis for FBP (x, ρ) (x, r, ϑ) 8

Intro Review Back Projection Factorization Conclusion Credits Equations (high-level) Sub Aperture partitioned signal: Back projected signal: Recursively partition the summation to shorter sub apertures. After finer resolution is obtained, switch back to Cartesian. 9

Intro Review Back Projection Factorization Conclusion Credits Aperture partitioning [MMM] Beamformation in each stage [ n M M log. M ] New back projected data is interpolated from previous beams. 10

Intro Review Back Projection Factorization Conclusion Credits • Back projected integral recursive partition + Aperture factorization + polar coordinates = faster back projection • Works for non-linear tracks • Accuracy of time-domain + efficiency of fast transform (FKA, FH) • Less memory compared to freq-domain algorithms • Further: angular interpolation, block factorization, error analysis (range error, non-linear track error, bounds) 11

Intro Review Back Projection Factorization Conclusion Credits • Review: Allen. C, Paden. J, “Interferometric SAR”(Spring 2021). • Review: Cumming, I. and F. Wong. “Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation. ” (2005). • FFBP: L. M. H. Ulander, H. Hellsten and G. Stenstrom, "Synthetic-aperture radar processing using fast factorized back-projection, " in IEEE Transactions on Aerospace and Electronic Systems, vol. 39, no. 3, pp. 760776, July 2003, doi: 10. 1109/TAES. 2003. 1238734. 12

Than. KU TALASILA HARA MADHAV 13