Fast Elimination of Redundant Linear Equations and Reconstruction

Fast Elimination of Redundant Linear Equations and Reconstruction of Recombination-free Mendelian Inheritance on a Pedigree Authors: Lan Liu & Tao Jiang, Univ. California, Riverside Jing Xiao, Lirong Xia, Tsinghua Univ. , China

Outline Ø n n Introduction and problem definition A new system of linear equations for ZRHC An O(mn 3) time algorithm for ZRHC An improved algorithm for ZRHC Conclusion

Pedigree n An example: British Royal Family

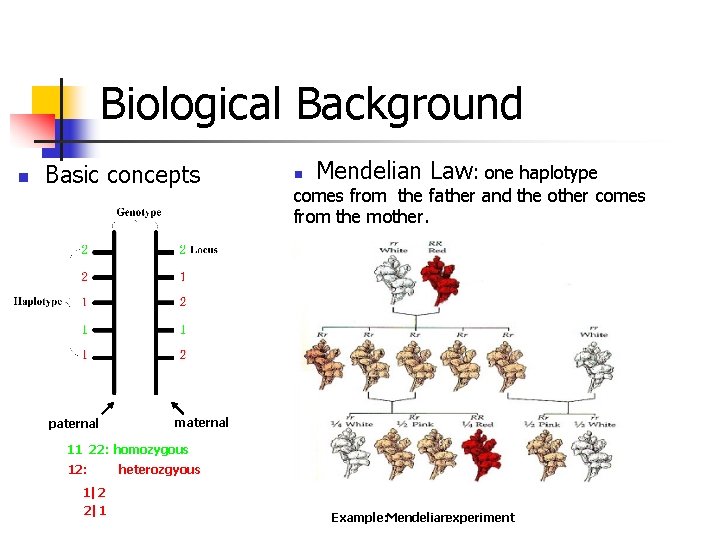
Biological Background n Basic concepts paternal n Mendelian Law: one haplotype comes from the father and the other comes from the mother. maternal 11 22: homozygous 12: 1|2 2|1 heterozgyous Example: Mendelianexperiment

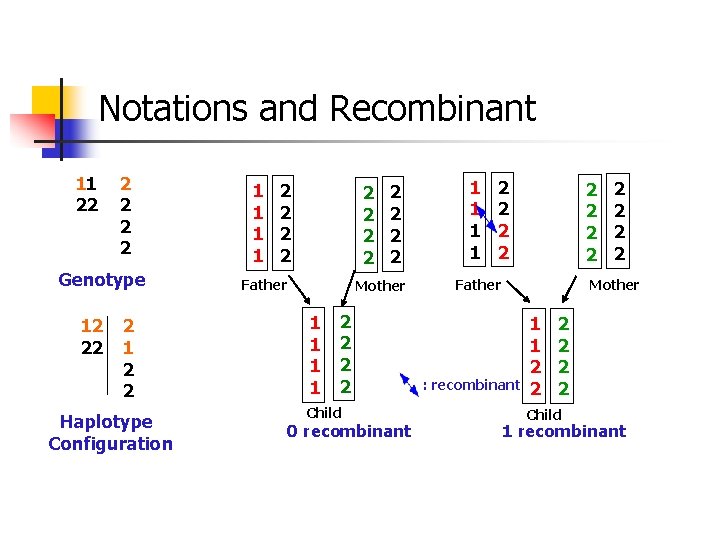
Notations and Recombinant 11 22 2 2 Genotype 12 22 2 1 2 2 Haplotype Configuration 1 1 2 2 2 2 Father 2 2 Mother 1 1 2 2 Child 0 recombinant 1 1 2 2 2 2 Father 2 2 Mother : recombinant 1 1 2 2 2 Child 1 recombinant

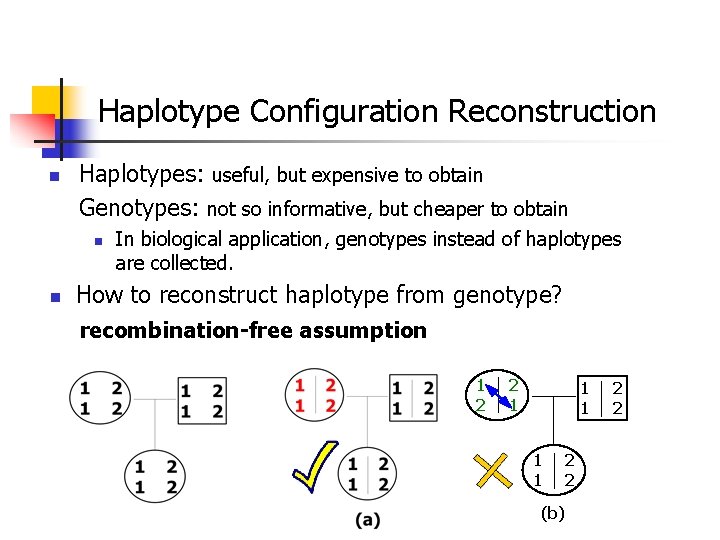
Haplotype Configuration Reconstruction n Haplotypes: useful, but expensive to obtain Genotypes: not so informative, but cheaper to obtain n n In biological application, genotypes instead of haplotypes are collected. How to reconstruct haplotype from genotype? recombination-free assumption 1 2 2 1 1 1 (b) 2 2

The ZRHC problem n Problem definition Given a pedigreeand the genotypeinformation for each member, find a recombination-free haplotype configurationfor each member that obeys the Mendelianlaw of inheritance.

Previous Work n n n Li and Jiang introduced a system of linear equations over F[2] and presented an time algorithm for ZRHC [LJ 03] , where m is #loci and n is #members in pedigree. Several attempts have been made recently, but the authors failed to prove the correctness of their algorithms in all cases, especially when the input pedigree has mating loops [CZ 04] [LCL 06]. Recently, Chan et al. proposed a linear-time algorithm in [CCC+06], which only works for pedigree without mating loops.

Related work n n n Methods based on fast matrix multiplication algorithms could achieve an asymptotic speed of O(k 2. 376) on k equations with k unknowns The Lanczos and conjugate gradient algorithms are only heuristics [GV 96]. The Wiedeman algorithm has expected quadratic running time [W 86]

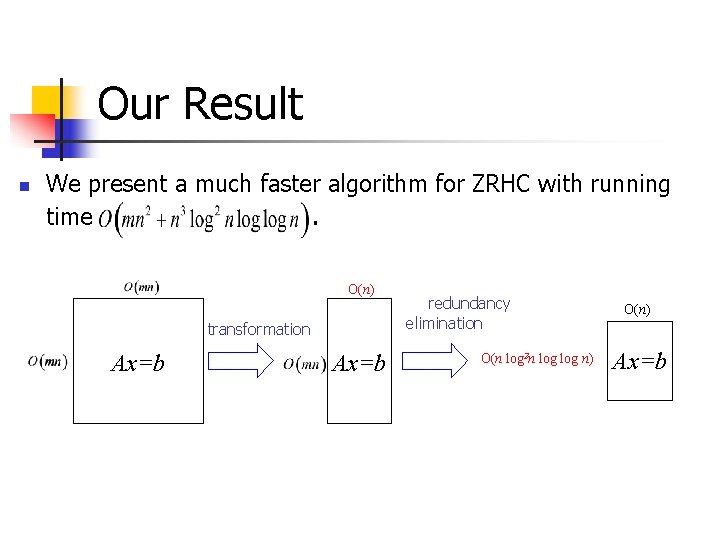
Our Result n We present a much faster algorithm for ZRHC with running time. O(n) transformation Ax=b redundancy elimination O(n log 2 n log n) O(n) Ax=b

Outline § Introduction and problem definition Ø n n n A new system of linear equations for ZRHC An O(mn 3) time algorithm for ZRHC An improved algorithm for ZRHC Conclusion Ax=b

The New Linear System n n, m n n m : #loci n: #members in pedigree Unknowns n : the paternal haplotype vector of a member j. : the scalar demonstrating inheritance info between a parent j 1 and a child j. n

The New Linear System j 2 j 1 0 0 1 1 0 0 0 0 j 0 0 0 1 1 1 0 1 pj 1, 2=1 pj 1, 3=0 0 1 1 1 j 2 j 1 Pj 1, 1 pj 1, 2 pj 1, 3 pj 1, 4 Pj 1, 1 +1 pj 1, 2 +0 pj 1, 3 +0 pj 1, 4 +1 Pj 1 +wj 1 hj 1, j Pj 2, 1 pj 2, 2 pj 2, 3 pj 2, 4 Pj 2 h j 2, j j Pj, 1 pj, 2 pj, 3 pj, 4 Pj Pj 2, 1 +0 pj 2, 2 +1 pj 2, 3 +1 pj 2, 4 +1 Pj 2 +wj 2 Pj, 1 +1 pj, 2 +1 pj, 3 +0 pj, 4 +0 Pj +wj

The Linear System § O(mn) equations on O(mn) unknowns. § Given a homozygous locus i on a member j (with a child j 1), pj[i] and pj 1[i] are pre-determined.

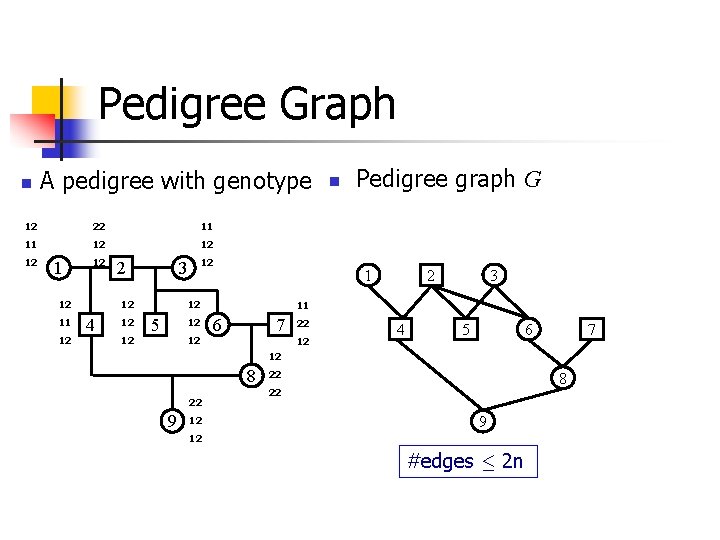
Pedigree Graph n A pedigree with genotype 12 22 11 11 12 12 12 11 12 2 3 12 4 12 12 12 Pedigree graph G 2 1 12 5 n 3 11 7 6 22 12 4 5 7 6 12 8 22 9 12 22 8 22 9 12 #edges · 2 n

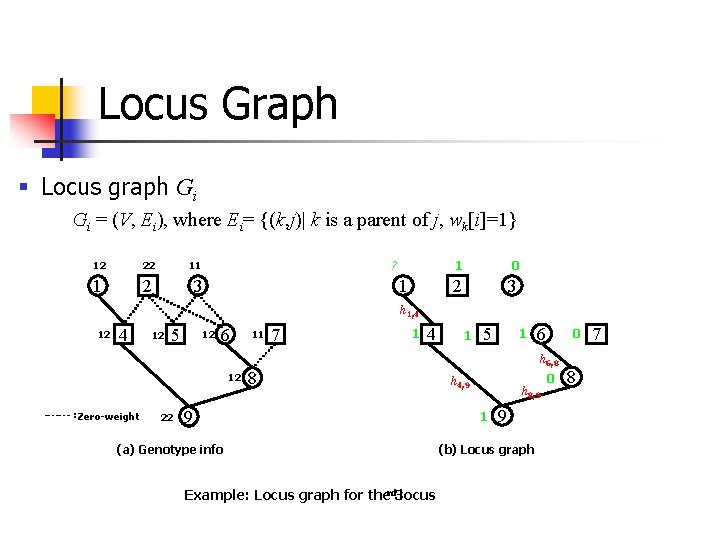
Locus Graph § Locus graph Gi Gi = (V, Ei), where Ei= {(k, j)| k is a parent of j, wk[i]=1} ? 12 22 11 1 2 3 1 1 0 2 3 h 1, 4 12 5 12 6 11 7 1 4 1 5 1 6 0 h 6, 8 12 Zero-weight 22 8 9 (a) Genotype info Example: Locus graph for therd 3 locus h 4, 9 h 8, 9 1 9 (b) Locus graph 0 8 7 :

Outline n n Ø n n Introduction and problem definition A new system of linear equations for ZRHC An O(mn 3) time algorithm for ZRHC An improved algorithm for ZRHC Conclusion O(n) transformation Ax=b O(mn) Ax=b

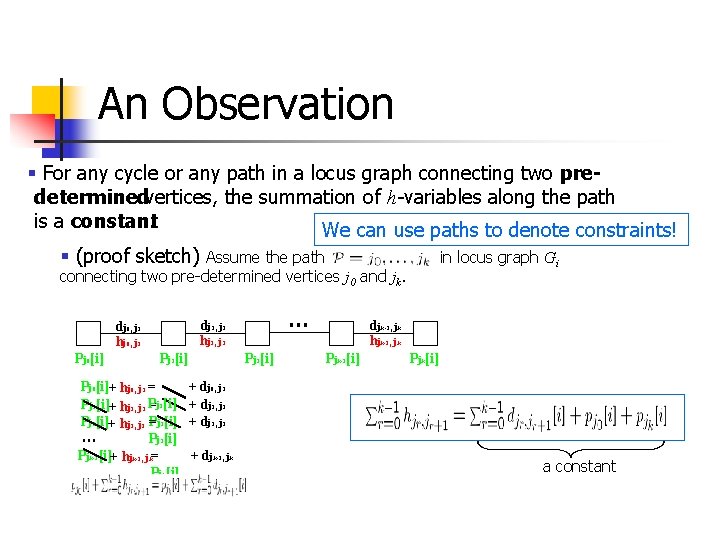
An Observation § For any cycle or any path in a locus graph connecting two predeterminedvertices, the summation of h-variables along the path is a constant. We can use paths to denote constraints! § (proof sketch) Assume the path connecting two pre-determined vertices j 0 and jk. Pj 0[i] … dj 1, j 2 hj 1, j 2 dj 0, j 1 hj 0, j 1 Pj 1[i] Pj 0[i]+ hj 0, j 1 = Pj 1[i]+ hj 1, j 2 P =j 1[i] Pj 2[i]+ hj 2, j 2 = … Pj 3[i] Pjk-1[i]+ hjk-1, jk= Pjk[i] Pj 2[i] in locus graph Gi djk-1, jk hjk-1, jk Pjk-1[i] Pjk[i] + dj 0, j 1 + dj 1, j 2 + dj 2, j 3 + djk-1, jk a constant

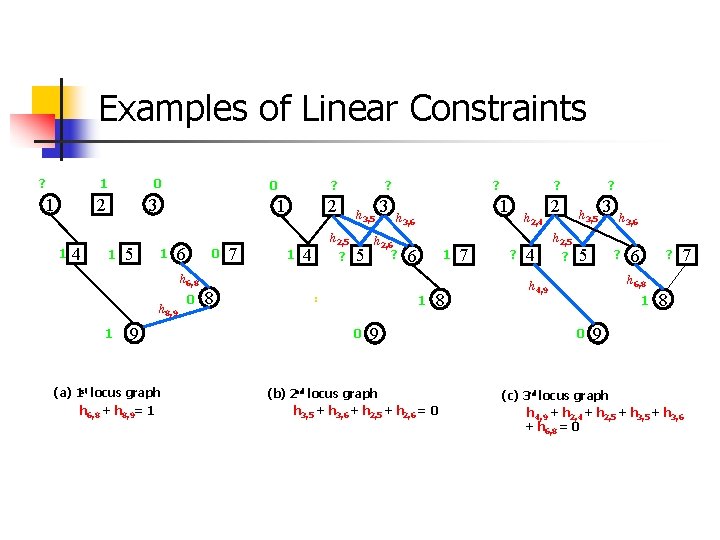
Examples of Linear Constraints ? 1 0 2 1 1 4 0 3 1 5 ? 2 1 1 6 0 7 ? 1 h 3, 5 h 2, 5 4 ? 5 3 ? 1 h 3, 6 h 2, 6 ? 6 1 h 6, 8 h 8, 9 1 9 (a) 1 st locus graph h 6, 8 + h 8, 9= 1 0 8 : 1 0 ? 8 9 (b) 2 nd locus graph h 3, 5 + h 3, 6 + h 2, 5 + h 2, 6 = 0 7 h 2, 4 ? 2 h 3, 5 h 2, 5 ? 5 3 h 3, 6 ? 7 h 6, 8 h 4, 9 1 0 8 9 (c) 3 rd locus graph h 4, 9 + h 2, 4 + h 2, 5 + h 3, 6 + h 6, 8 = 0

Linear Constraints Obviously, the linear constraints are necessary. We can also show that these constraints are sufficient. n Moreover, we can upper bound #constraints in each locus graph as O(n), while the trivial analysis gives an upper bound O(n 2). n Total #constraints = O(mn). n

The ZRHC-PHASE algorithm Algorithm. ZRHC_PHASE Traditional method input: a pedigree G=(V, E) and genotype {gj} § Solve h-variables and p- output: a general solution of {pj} begin Step 1. Preprocessing Step 2. Linear constraint generation on h-variables Step 3. Solve h-variables by Gaussian Elimination Step 4. Solve the p-variables by propagation from pre -determined p-variables to others. end variables together § O(mn) equations on O(mn) unknowns: O(mn) p-variables and O(n) h-variables. Our method § Solve h-variables and pvariables separately § O(mn) linear equations on O(n) h-variables.

Outline n n n Ø n Introduction and problem definition A new system of linear equations for ZRHC An O(mn 3) time algorithm for ZRHC An improved algorithm for ZRHC Conclusion O(n) transformation Ax=b O(mn) Ax=b redundancy elimination O(n log 2 n log n) O(n) Ax=b

Redundant Equation Elimination n An observation j 0 j 1 Given a cycle , assume that there are constraints among each pair of vertices. n j 2 jk … jk-2 jk-1 j 0 ~ j 2 ~ jk-1 j 0 ~ jk-1 n Key lemma Originally, there are O(k 2) constraints. Notice that they are not independent. n However, we can replace the original constraints by an equivalent set of constraints with size O(k). n Remove the redundant equations without solving them!

Redundant Equation Elimination Given a spanning tree, the stretchof an edge (k, j) is defined as the length of the unique path between k and j on the tree. n Elkin, Emeky, Spielman and Teng shows that we can embed any graph in a low-stretchspanning tree with average stretch O(log 2 n log n). n The number of irredundant constraints can be bounded by the sum of cycle lengths , which is further bounded by the sum of stretches. O(nlog 2 n log n). n

Conclusion n We present an efficient algorithm for ZRHC with running time O(mn 2+n 3 log 2 n log n). It remains interesting if the time complexity for ZRHC on general pedigrees can be improved to O(mn 2+n 3) or lower. Another open question is how to use the algorithm to get haplotype configurations on pedigrees that require only a small (constant) number of recombinants

Thanks for your time and attention!