Fast Computation of Generalized Voronoi Diagrams Using Graphics

Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware Kenneth E. Hoff III, Tim Culver, John Keyser, Ming Lin, and Dinesh Manocha University of North Carolina at Chapel Hill SIGGRAPH ‘ 99

What is a Voronoi Diagram? Given a collection of geometric primitives, it is a subdivision of space into cells such that all points in a cell are closer to one primitive than to any other Voronoi Site Voronoi Region

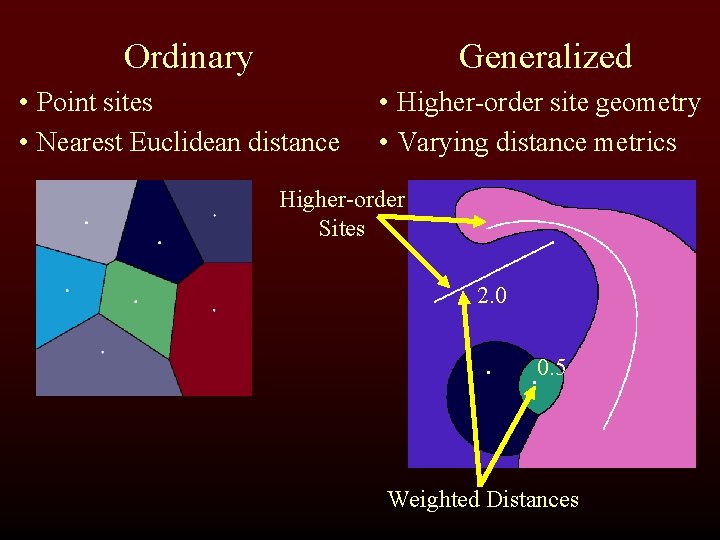
Ordinary Generalized • Point sites • Nearest Euclidean distance • Higher-order site geometry • Varying distance metrics Higher-order Sites 2. 0 0. 5 Weighted Distances

Why Should We Compute Them? It is a fundamental concept Descartes Dirichlet Voronoi Boldyrev Thiessen Niggli Wigner & Seitz Frank & Casper Brown Mead Hoofd et al. Icke Astronomy Math Geology Meteorology Crystallography Physics Ecology Anatomy Astronomy 1644 1850 1908 1909 1911 1927 1933 1958 1965 1966 1985 1987 “Heavens” Dirichlet tesselation Voronoi diagram area of influence polygons Theissen polygons domains of action Wigner-Seitz regions atom domains areas potentially available plant polygons capillary domains Voronoi diagram

Why Should We Compute Them? Useful in a wide variety of applications Collision Detection Surface Reconstruction Robot Motion Planning Non-Photorealistic Rendering Surface Simplification Mesh Generation Shape Analysis

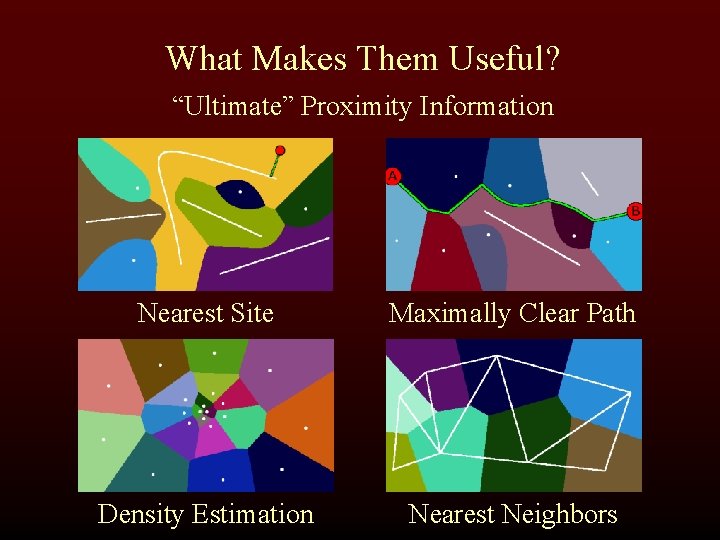
What Makes Them Useful? “Ultimate” Proximity Information Nearest Site Maximally Clear Path Density Estimation Nearest Neighbors

Outline • Generalized Voronoi Diagram Computation • • • – Exact and Approximate Algorithms – Previous Work – Our Goal Basic Idea Our Approach Basic Queries Applications Conclusion

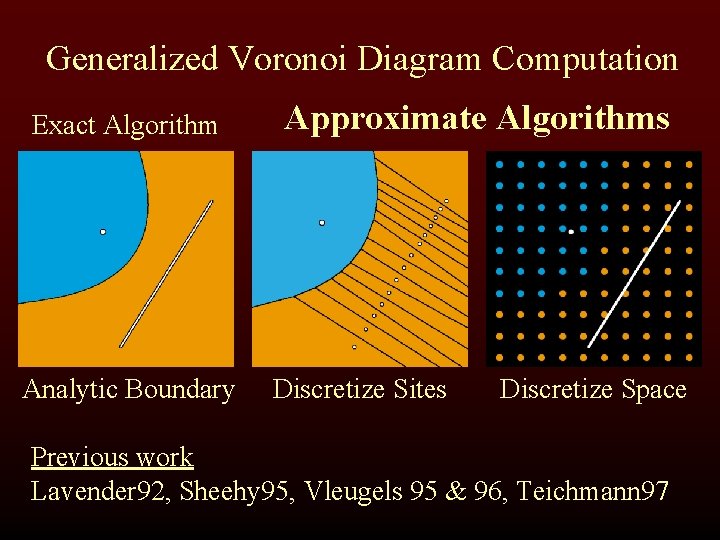
Generalized Voronoi Diagram Computation “Exact” Algorithms Previous work Computes Analytic Boundary • Lee 82 • Chiang 92 • Okabe 92 • Dutta 93 • Milenkovic 93 • Hoffmann 94 • Sherbrooke 95 • Held 97 • Culver 99

Previous Work: “Exact” Algorithms • Compute analytic boundaries but. . . • Boundaries composed of high-degree curves and surfaces and their intersections • Complex and difficult to implement • Robustness and accuracy problems

Generalized Voronoi Diagram Computation Exact Algorithm Analytic Boundary Approximate Algorithms Discretize Sites Discretize Space Previous work Lavender 92, Sheehy 95, Vleugels 95 & 96, Teichmann 97

Previous Work: Approximate Algorithms • Provide practical solutions but. . . • Difficult to error-bound • Restricted to static geometry • Relatively slow

Our Goal Approximate generalized Voronoi diagram computation that is: • Simple to understand implement • Easily generalized • Efficient and practical with all sources of error fully enumerated

Outline • Generalized Voronoi Diagram Computation • Basic Idea • • – Brute-force Algorithm – Cone Drawing – Graphics Hardware Acceleration Our Approach Basic Queries Applications Conclusion

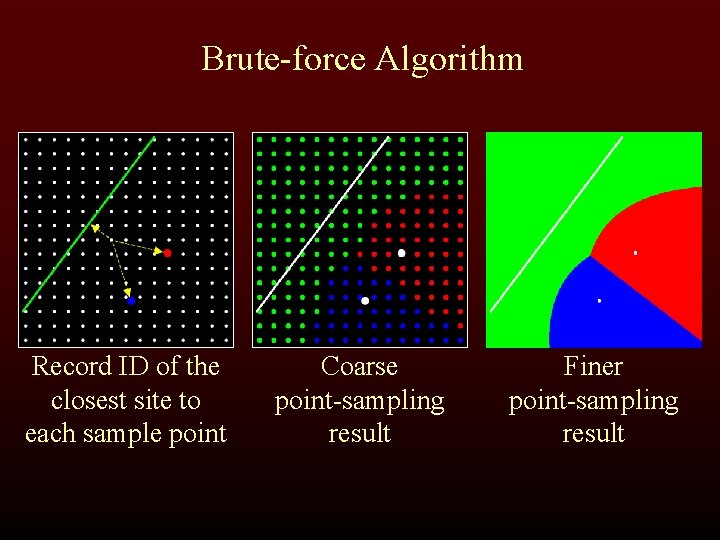
Brute-force Algorithm Record ID of the closest site to each sample point Coarse point-sampling result Finer point-sampling result

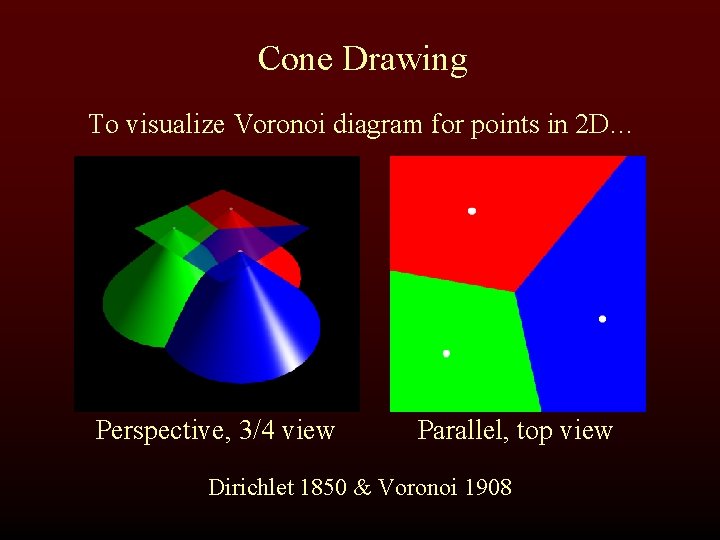
Cone Drawing To visualize Voronoi diagram for points in 2 D… Perspective, 3/4 view Parallel, top view Dirichlet 1850 & Voronoi 1908

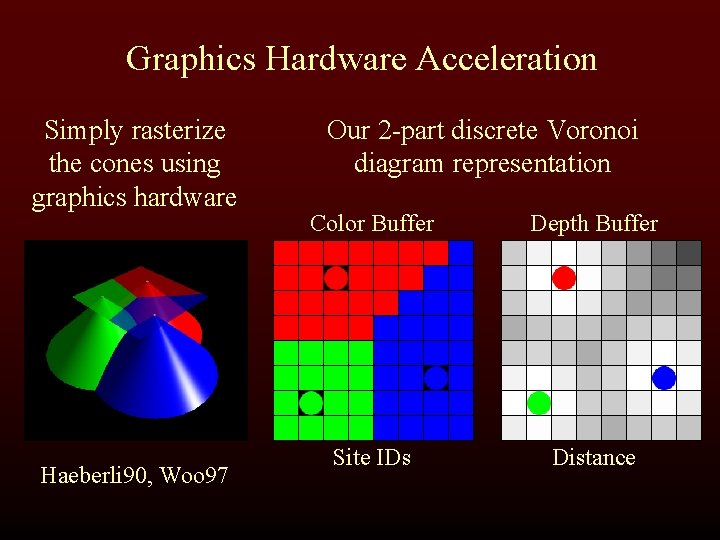
Graphics Hardware Acceleration Simply rasterize the cones using graphics hardware Haeberli 90, Woo 97 Our 2 -part discrete Voronoi diagram representation Color Buffer Depth Buffer Site IDs Distance

Outline • Generalized Voronoi Diagram Computation • Basic Idea • Our Approach – Meshing Distance Function – Generalizations – 3 D – Sources of Error • Basic Queries • Applications • Conclusion

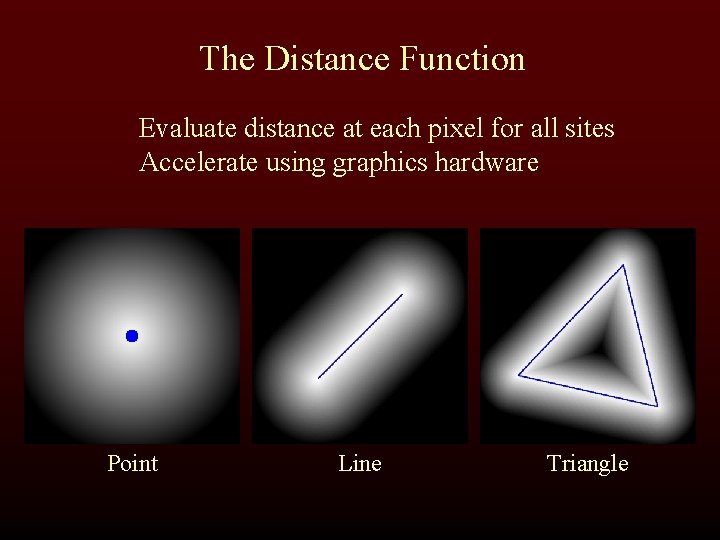
The Distance Function Evaluate distance at each pixel for all sites Accelerate using graphics hardware Point Line Triangle

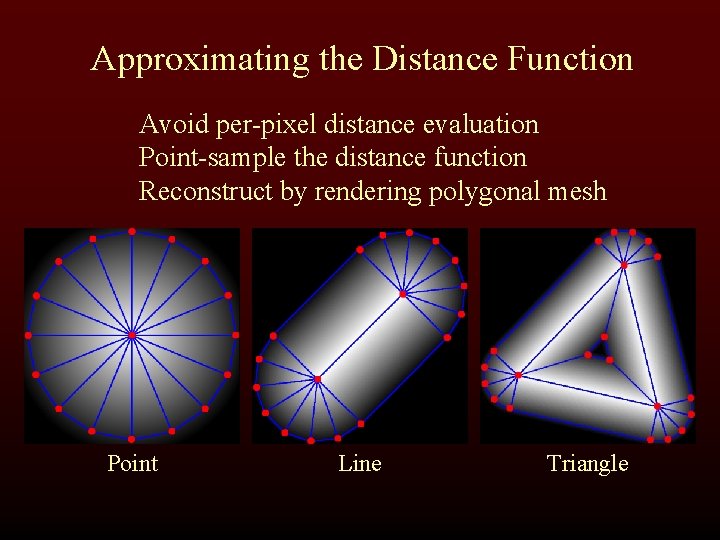
Approximating the Distance Function Avoid per-pixel distance evaluation Point-sample the distance function Reconstruct by rendering polygonal mesh Point Line Triangle

The Error Bound Error bound is determined by the pixel resolution farthest distance a point can be from a pixel sample point Close-up of pixel grid

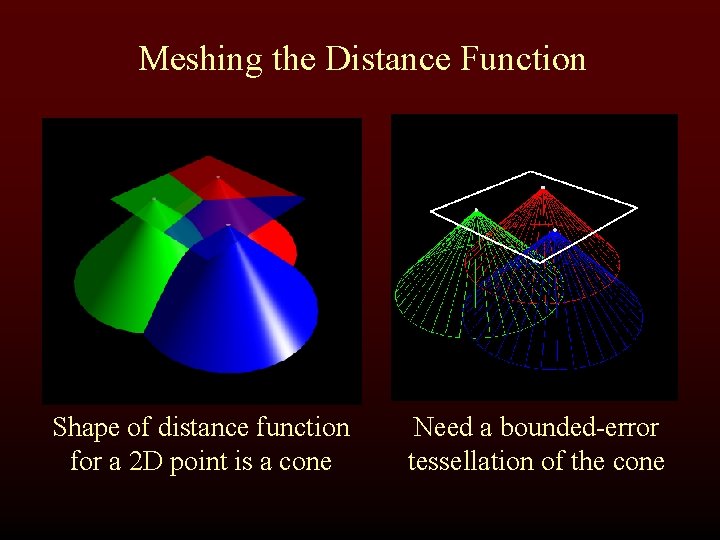
Meshing the Distance Function Shape of distance function for a 2 D point is a cone Need a bounded-error tessellation of the cone

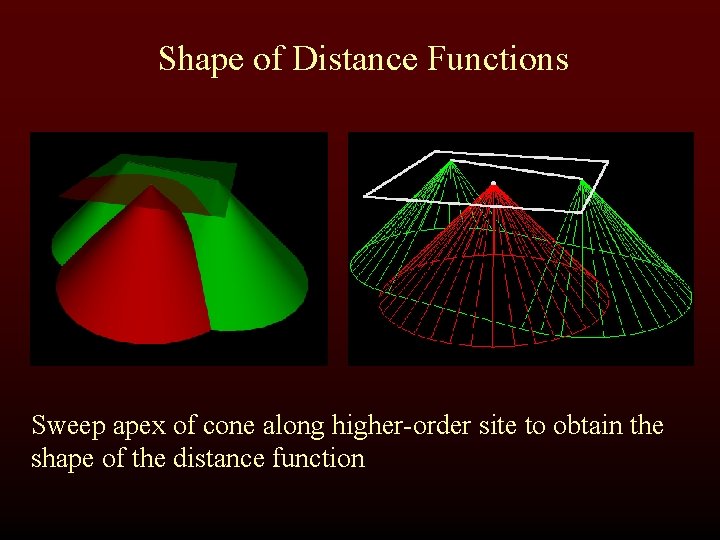
Shape of Distance Functions Sweep apex of cone along higher-order site to obtain the shape of the distance function

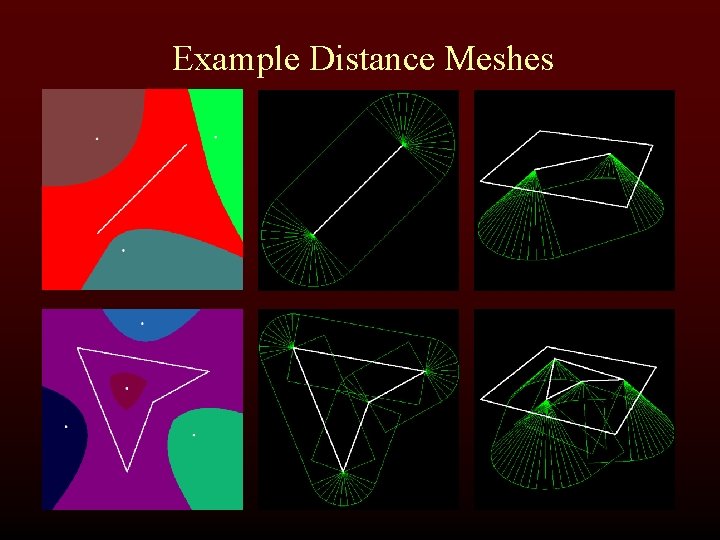
Example Distance Meshes

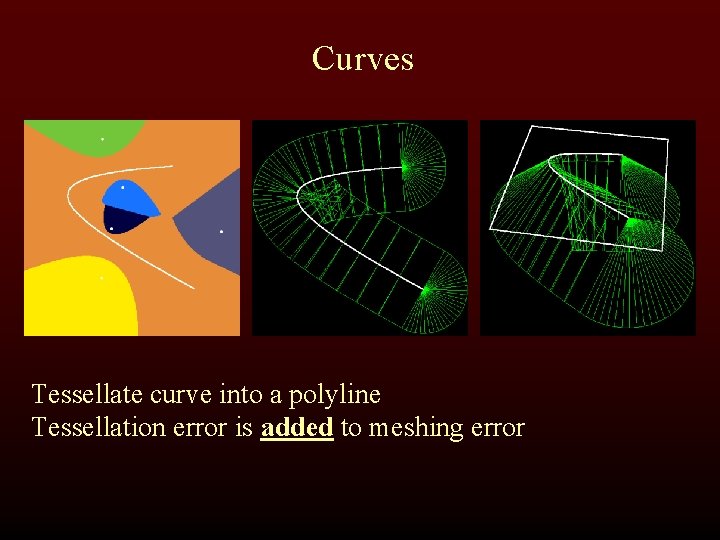
Curves Tessellate curve into a polyline Tessellation error is added to meshing error

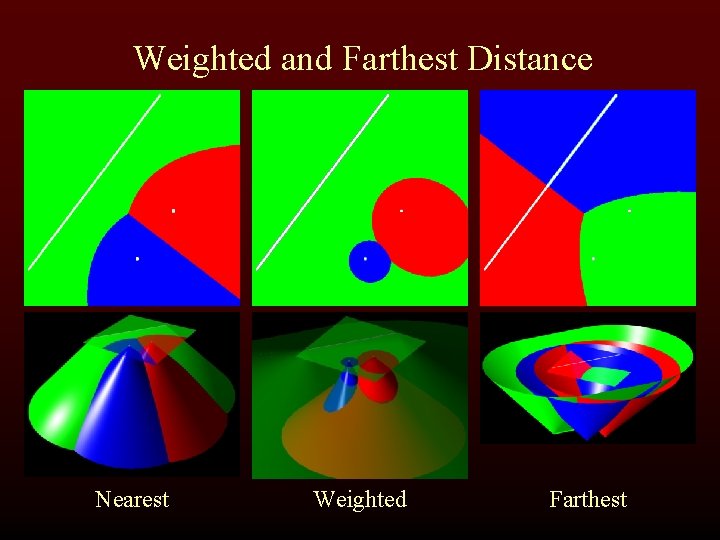
Weighted and Farthest Distance Nearest Weighted Farthest

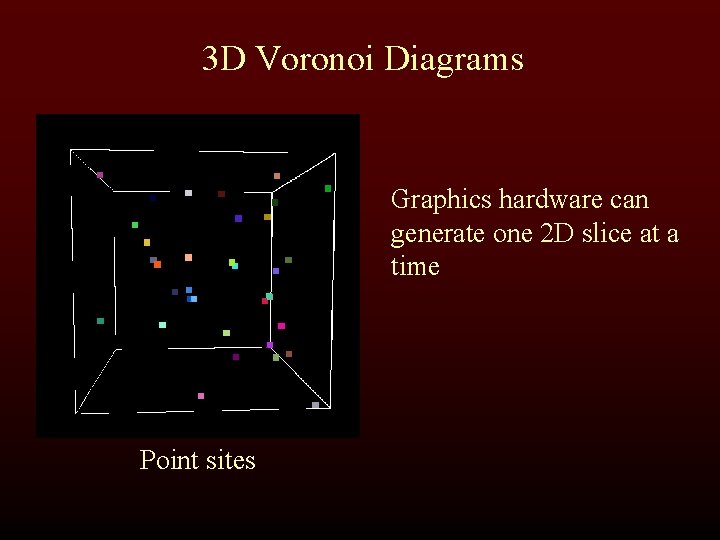
3 D Voronoi Diagrams Graphics hardware can generate one 2 D slice at a time Point sites

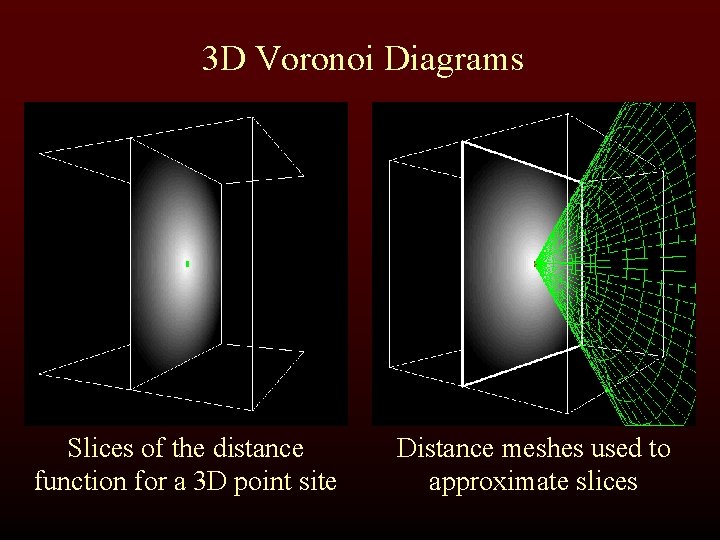
3 D Voronoi Diagrams Slices of the distance function for a 3 D point site Distance meshes used to approximate slices

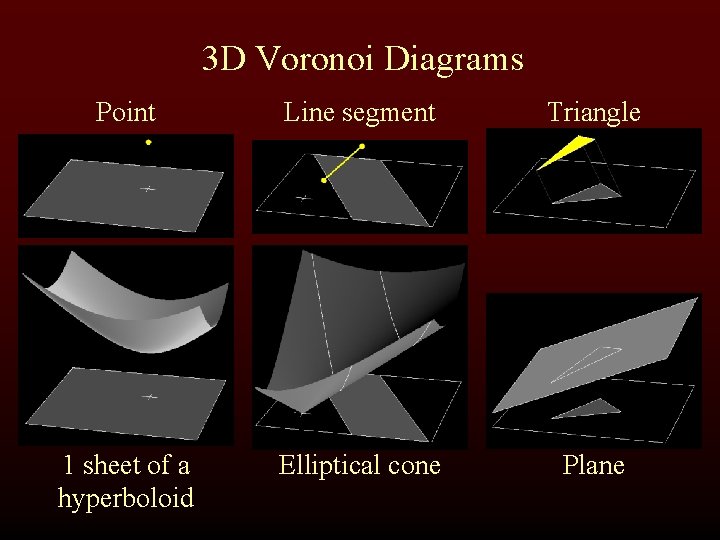
3 D Voronoi Diagrams Point Line segment Triangle 1 sheet of a hyperboloid Elliptical cone Plane

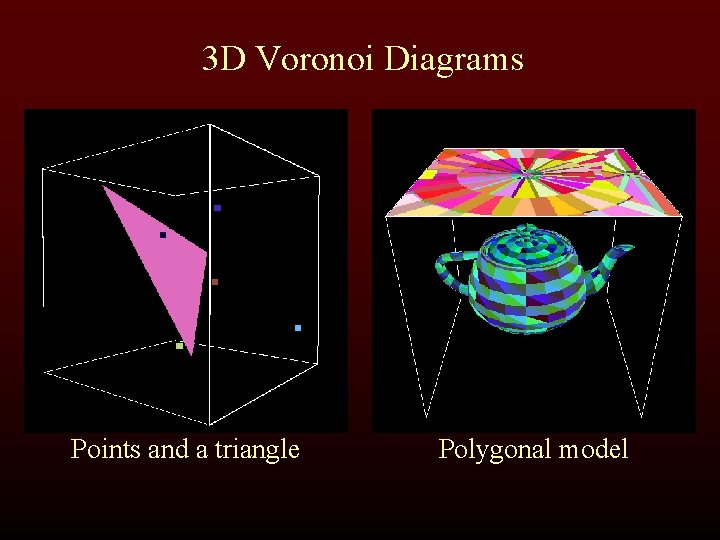
3 D Voronoi Diagrams Points and a triangle Polygonal model

Sources of Error • Distance Error – Meshing – Tessellation – Hardware Precision • Combinatorial Error – Distance – Pixel Resolution – Z-buffer Precision

Adaptive Resolution Zoom in to reduce resolution error. . .

Outline • Generalized Voronoi Diagram Computation • Basic Idea • Our Approach • Basic Queries – Nearest Site – Boundary Finding – Nearest-Neighbor Finding – Maximally Clear Point • Applications • Conclusion

Nearest Site Table lookup on query point

Boundary Finding • Isosurface extraction : boundary walking • Offset difference image to mark boundary pixels

Nearest-Neighbor Finding • Which colors touch in the image? • Walk the boundaries (like boundary finding)

Maximally Clear Point with the largest depth value (greatest distance)

Outline • • Generalized Voronoi Diagram Computation Basic Idea Our Approach Basic Operations • Applications – Motion Planning – Medial Axis Computation – Dynamic Mosaics • Conclusion

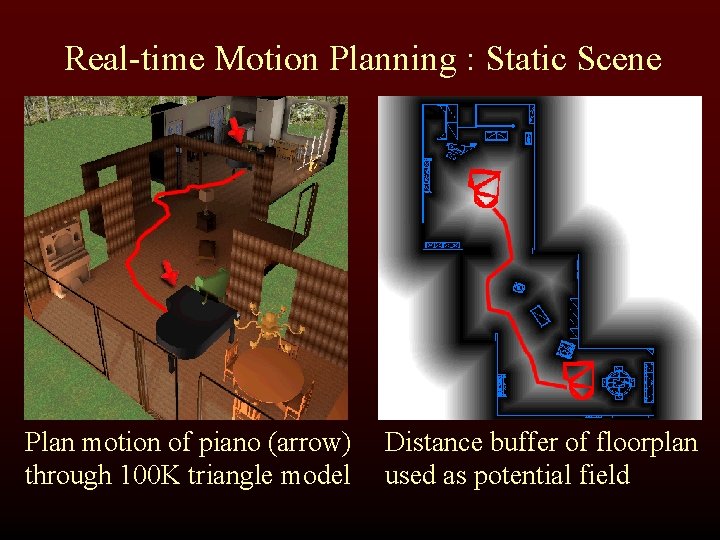
Real-time Motion Planning : Static Scene Plan motion of piano (arrow) through 100 K triangle model Distance buffer of floorplan used as potential field

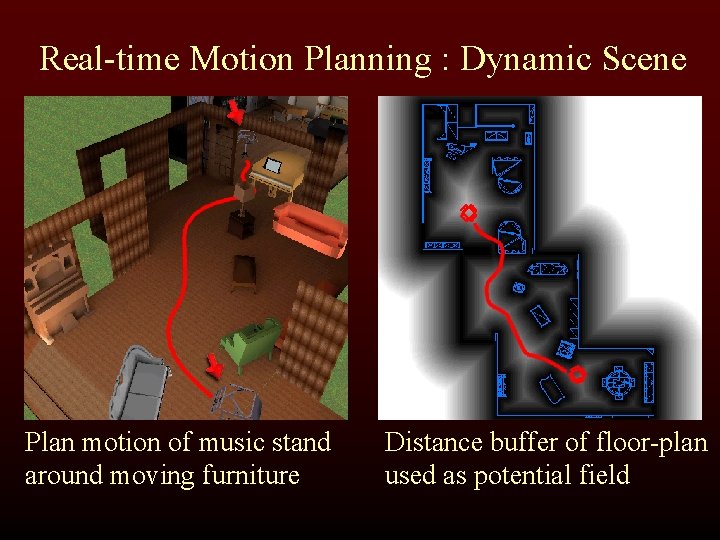
Real-time Motion Planning : Dynamic Scene Plan motion of music stand around moving furniture Distance buffer of floor-plan used as potential field

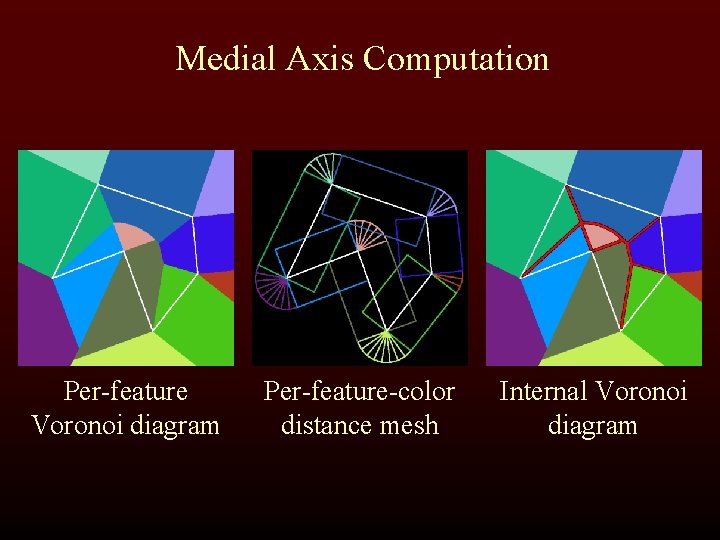
Medial Axis Computation Per-feature Voronoi diagram Per-feature-color distance mesh Internal Voronoi diagram

Dynamic Mosaics 1000 moving points Source image Dynamic Mosaic Tiling Static mosaics by Paul Haeberli in SIGGRAPH ‘ 90

Outline • • • Generalized Voronoi Diagram Computation Basic Idea Our Approach Basic Operations Applications • Conclusion

Conclusion + Meshing Distance Functions Graphics Hardware Acceleration Brute-force Approach Fast and Simple, Approximate Generalized Voronoi Diagrams Bounded Error

Future Work • Improve distance meshing for 3 D primitives • More applications – Motion planning with more degrees of freedom – Accelerate exact Voronoi diagram computation – Surface reconstruction – Medical imaging: segmentation and registration – Finite-element mesh generation

Acknowledgements Sarah Hoff Chris Weigle Stefan Gottschalk Mark Peercy UNC Computer Science SGI Advanced Graphics Berkeley Walkthrough Group

Acknowledgements Army Research Office National Institute of Health National Science Foundation Office of Naval Research Intel

Live Demo. . .