Fast calculation of FP cavity for modal model

Fast calculation of FP cavity for modal model Keiko Kokeyama Ochanomizu University And National Astronomical Observatory of Japan

Contents • • • Introduction Basic formulae Approximations Simulation result Summary 1

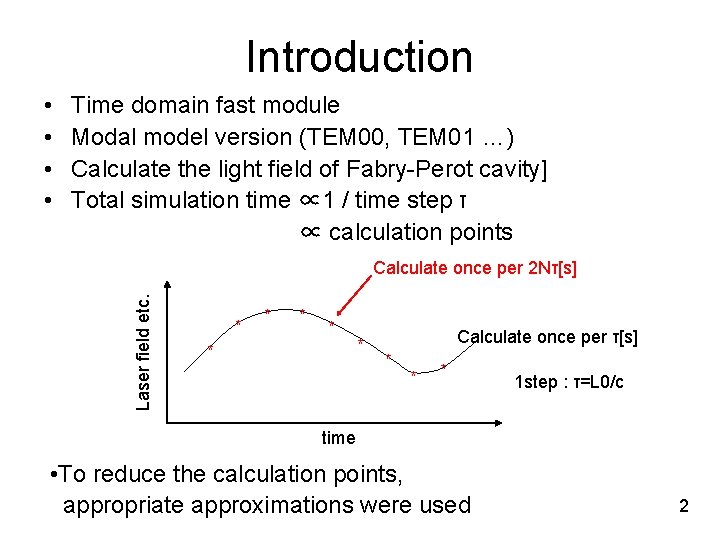
Introduction • • Time domain fast module Modal model version (TEM 00, TEM 01 …) Calculate the light field of Fabry-Perot cavity] Total simulation time ∝ 1 / time step τ ∝ calculation points Laser field etc. Calculate once per 2 Nτ[s] * * * Calculate once per τ[s] * * * 1 step : τ=L 0/c time • To reduce the calculation points, appropriate approximations were used 2

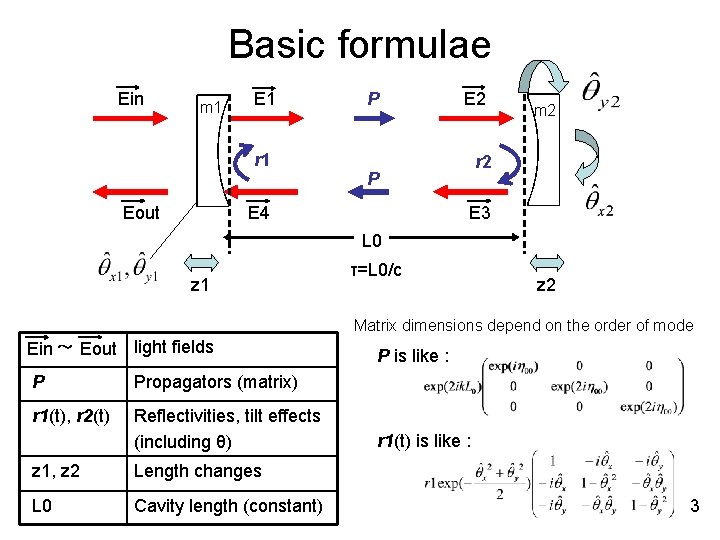
Basic formulae Ein m 1 E 1 r 1 Eout P E 2 r 2 P E 4 m 2 E 3 L 0 z 1 τ=L 0/c z 2 Matrix dimensions depend on the order of mode Ein ～ Eout light fields P Propagators (matrix) r 1(t), r 2(t) Reflectivities, tilt effects (including θ) z 1, z 2 Length changes L 0 Cavity length (constant) P is like : r 1(t) is like : 3

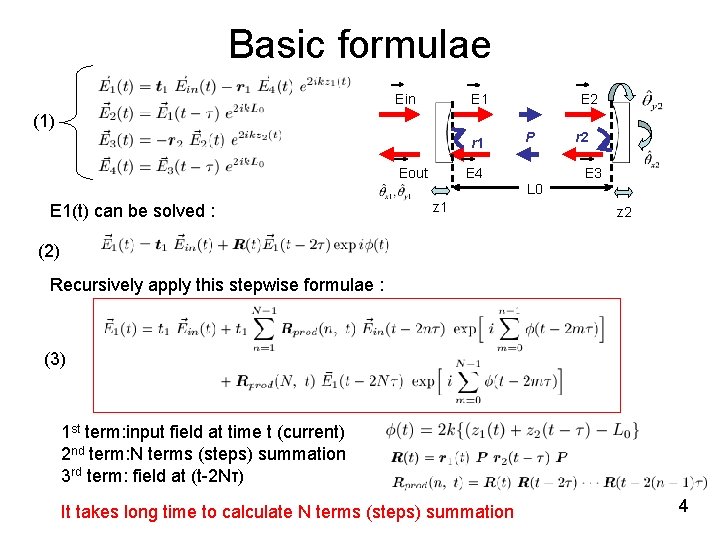
Basic formulae Ein (1) r 1 Eout E 1(t) can be solved : E 2 E 1 E 4 z 1 P L 0 r 2 E 3 z 2 (2) Recursively apply this stepwise formulae : (3) 1 st term: input field at time t (current) 2 nd term: N terms (steps) summation 3 rd term: field at (t-2 Nτ) It takes long time to calculate N terms (steps) summation 4

Approximation By using linear approximation, that is, by assuming that all physics quantities change linear in time, one step calculation gives the current field with the field 2 N τ [s] before N times summation without any approximations (3) Linear approximation for mirror positions and tilt angles r 1(t), r 2(t) depend on tilts θ Some further approximation are used to express the final result in an explicit analytic from. (4) No summation with approximations 5

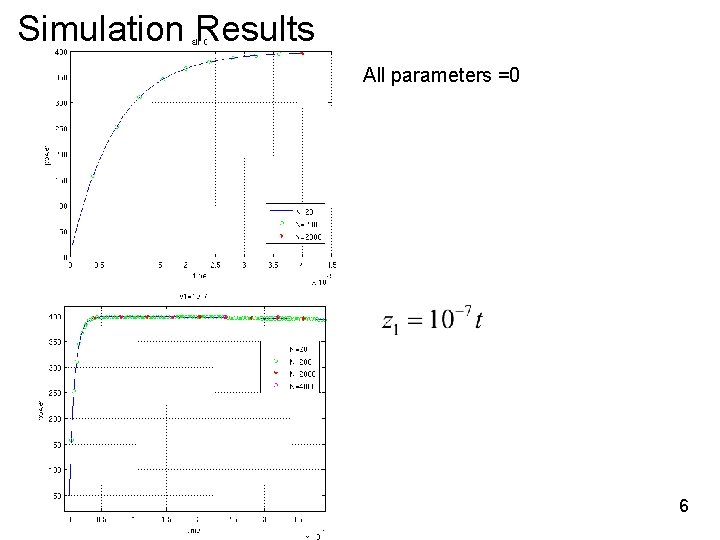
Simulation Results All parameters =0 6

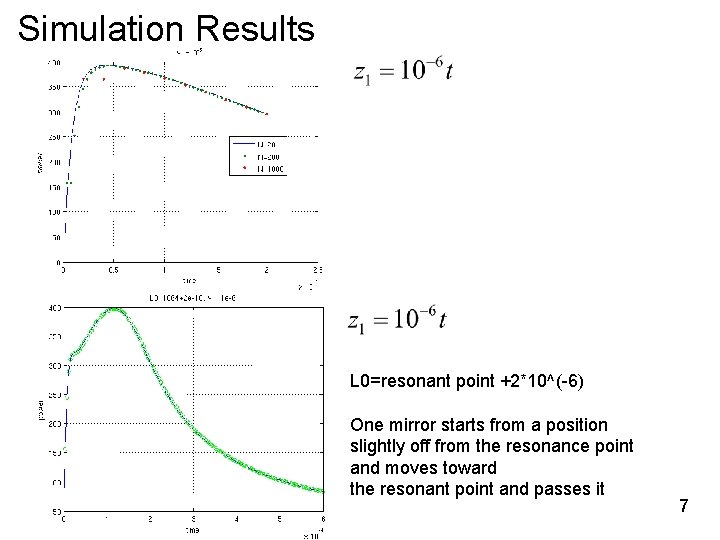
Simulation Results L 0=resonant point +2*10^(-6) One mirror starts from a position slightly off from the resonance point and moves toward the resonant point and passes it 7

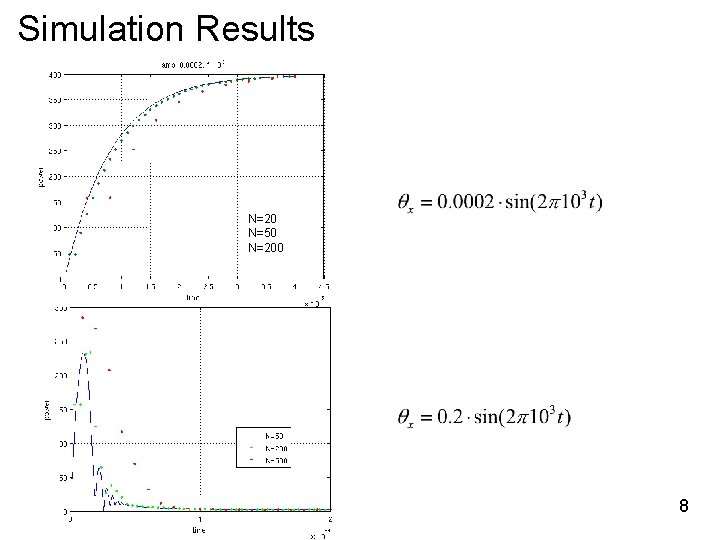
Simulation Results N=20 N=50 N=200 8

Summary • Approximation formulae were developed • Calculations became faster when N is big (100~) To do • Accuracy validation is undergoing (How big N is available? Any reference? ) • Compare with E 2 E calculation using primitive mirrors 9