Fast and MemoryEfficient Regular Expression Matching for Deep

Fast and Memory-Efficient Regular Expression Matching for Deep Packet Inspection Authors: Fang Yu, Zhifeng Chen, Yanlei Diao, T. V. Lakshman and Randy H. Katz Publisher: ANCS'06, December 3– 5, 2006 Present: Yu-Tso Chen Date: November, 6, 2007 Department of Computer Science and Information Engineering National Cheng Kung University, Taiwan R. O. C. 1

Outline l l l 1. Introduction 2. Definitions and problem description 3. Matching of Individual Patterns 4. Selective Grouping of Multiple Patterns 5. Evaluation Result 6. Conclusion 2

Introduction l Three unique complex features • 1) Large numbers of wildcards can cause DFA to • • grow exponentially 2) Wildcard are used with length restriction(‘? ’, ‘+’) will increase the resource 3) Groups of characters are also commonly used such interaction can result in highly complex state machine(ex. ”^220[x 09 -]*ftp”) 3

Introduction (cont. ) l Make following contributions • 1) Analyze the computational and storage cost of • • building individual DFAs 2) Two rewrite rules for specific regular expressions 3) Combine multiple DFAs into a small number of group 4

Outline l l l 1. Introduction 2. Definitions and problem description 3. Matching of Individual Patterns 4. Selective Grouping of Multiple Patterns 5. Evaluation Result 6. Conclusion 5

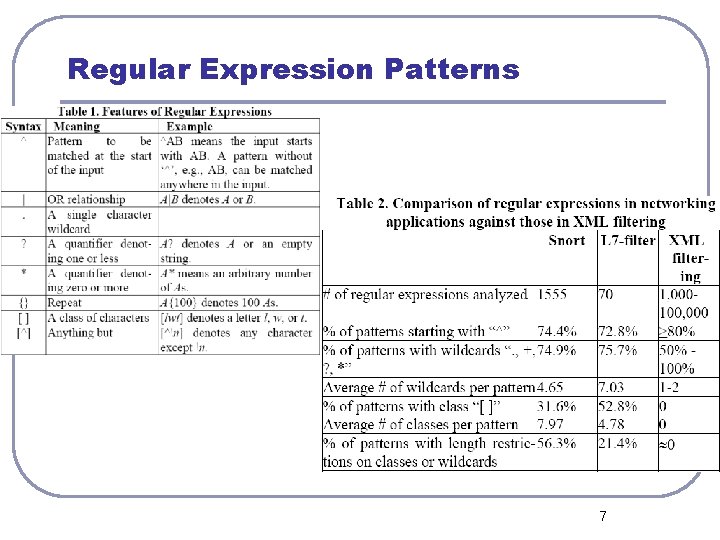
Regular Expression Patterns l Compares the regular expressions used in two networking applications (Snort, Linux L-7 filter & XML filtering) • 1)Both types of app. Use wildcards • • (‘. ’, ’? ‘, ’+’, ’*’) contain larger numbers of them 2) Classes of characters (“[ ]”) are used only in packet scanning applications 3) High percentage of scanning app. Have length restrictions on some of the classes or wildcards 6

Regular Expression Patterns 7

Solution Space for Regular Expression Matching l l l A single regular expression of length n can be expressed as an NFA with O(n) When the NFA is converted into a DFA, it may generate states The processing complexity for each character in the input is O(1) in DFA, but is O(n 2) for an NFA when all n states are active at the same time 8

Solution Space for Regular Expression Matching (cont. ) l To handle m regular expressions, two choices are possible： • Processing them individually in m automata • Compiling them into a single automaton 9

Problem Statement l DFA-based approaches in this paper • Our goal is to achieve O(1) computation cost • The focus of the study is to reduce memory overhead of DFA l There are two sources of memory usage in DFAs：states and transitions • We consider the number of states as the primary factor 10

Outline l l l 1. Introduction 2. Definitions and problem description 3. Matching of Individual Patterns 4. Selective Grouping of Multiple Patterns 5. Evaluation Result 6. Conclusion 11

Design Considerations l Define Completeness of Matching Results： • Exhaustive Matching：M(P, S)={substring S’ of S | S’ is accepted by the DFA of P} • It is expensive and often unnecessary to report all • • matching substrings We propose a new concept, Non-overlapping Matching, that relaxes the requirements of exhaustive matching Non-overlapping Matching： • Ex：ab* if input abbb non-overlapping matching will • report one match instead of three Exhaustive Matching will report, abb, abbb 12

Design Considerations (cont. ) l Define DFA Execution Model for Substring Matching：We focus on patterns without ‘^’ attached at the beginning • • Repeater searches One-pass search – this approach can truly achieve O(1) computation cost per character 13

DFA Analysis for Individual Regular Expressions l The study is based on the use of exhaustive matching & one-pass search 14

Case 4：DFA of Quadratic Size l The DFA needs to remember the number of Bs it has seen and their locations 15

Case 5：DFA of Exponential Size l An exponential number of states (22+1)are needed to represent these two wildcard characters AAB(AABBCD) is different from ABA(ABABCD) because a subsequence input BCD 16

Regular Expression Rewrites l Rewrite Rule(1) • “^SEARCHs+[^n]{1024}” to “^SEARCHs [^n]{1024}” • “^A+[A-Z]{j}” to “^A [A-Z]{j}” • We can prove match “^A+[A-Z]{j}” also match “^A [A-Z]{j}” 17

Regular Expression Rewrites (cont. ) l Rewrite Rule(2) • We don’t need to keep track of the second AUTHs • If there is a ‘n’ within the next 100 bytes, the return • • character must also be within 100 bytes to the second AUTHs If there is no ‘n’ within the next 100 bytes, the first already matched the pattern “([^A]|A[^U]|AU[^T]|AUT[^H]|AUTH[^s]|AUTHs[^n]{0, 99 }n)*AUTHs[^n]{100}” 18

Outline l l l 1. Introduction 2. Definitions and problem description 3. Matching of Individual Patterns 4. Selective Grouping of Multiple Patterns 5. Evaluation Result 6. Conclusion 19

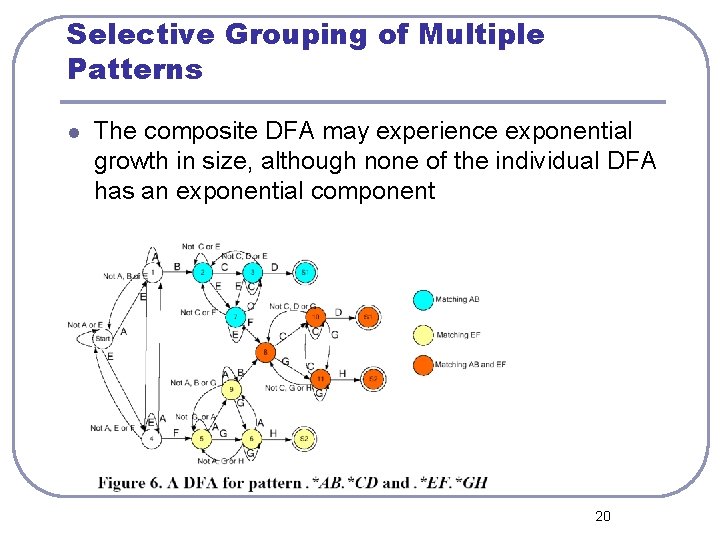
Selective Grouping of Multiple Patterns l The composite DFA may experience exponential growth in size, although none of the individual DFA has an exponential component 20

Regular Expressions Grouping Algorithm l Definition of interaction：two patterns interact with each other if their composite DFA contains more states than the sum of two individual ones 21

Grouping Algorithm 22

Outline l l l 1. Introduction 2. Definitions and problem description 3. Matching of Individual Patterns 4. Selective Grouping of Multiple Patterns 5. Evaluation Result 6. Conclusion 23

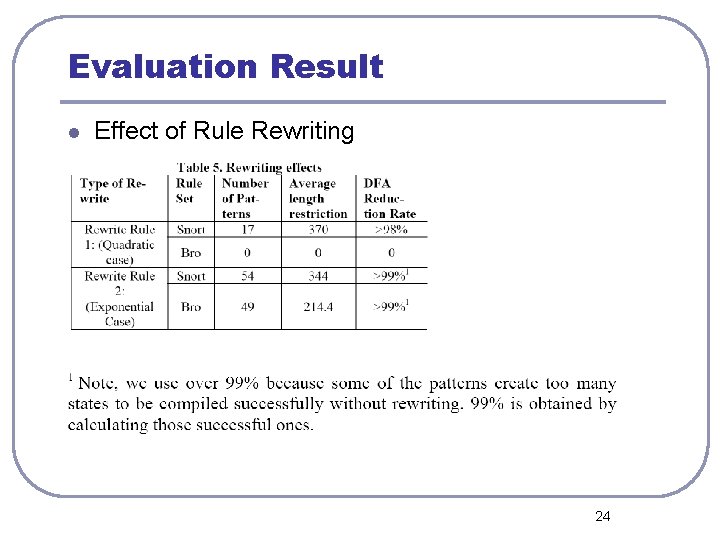
Evaluation Result l Effect of Rule Rewriting 24

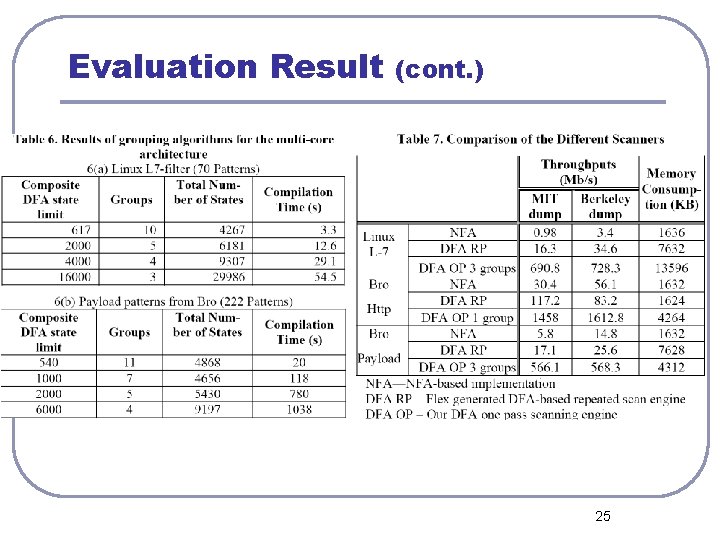
Evaluation Result (cont. ) 25

Outline l l l 1. Introduction 2. Definitions and problem description 3. Matching of Individual Patterns 4. Selective Grouping of Multiple Patterns 5. Evaluation Result 6. Conclusion 26

Conclusion l l Rewriting techniques – memory-efficient DFA-based approaches are possible Selectively groups patterns together – speed up the matching process 27