Fast Algorithm for Creating Space Efficient Dispatching Tables

Fast Algorithm for Creating Space -Efficient Dispatching Tables with Application to Multi-Dispatching Yoav Zibin Technion—Israel Institute of Technology Joint work with: Yossi (Joseph) Gil

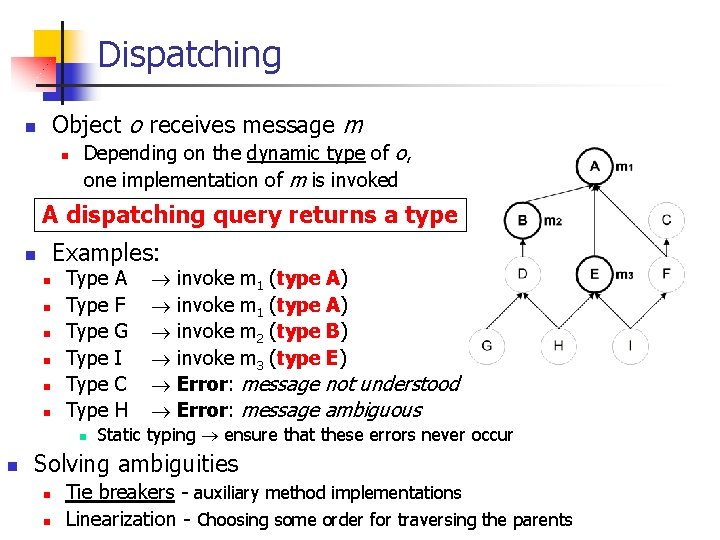
Dispatching Object o receives message m n n Depending on the dynamic type of o, one implementation of m is invoked A dispatching query returns a type Examples: n n n n Type Type n n A F G I C H invoke m 1 (type A) invoke m 2 (type B) invoke m 3 (type E) Error: message not understood Error: message ambiguous Static typing ensure that these errors never occur Solving ambiguities n n Tie breakers - auxiliary method implementations Linearization - Choosing some order for traversing the parents

The Dispatching Problem n n Encoding of a hierarchy: a data structure representing the hierarchy and the method families which supports dispatching queries. Metrics: n n Space requirement of the data structure Dispatch query time Creation time of the encoding Our results: n n n Space: superior to all previous algorithms Dispatch time: small, but not constant Creation time: almost linear

Problem Variations n Single vs. Multiple Inheritance (SI vs. MI) n n SI: a type has at most one direct supertype (tree/forest topology) MI: otherwise n n Batch vs. Incremental n n n Java: SI class hierarchy, MI type hierarchy. Batch (e. g. , Eiffel) the whole hierarchy is given at compile-time Incremental (e. g. , Java) the hierarchy is built at runtime Statically vs. Dynamically typed languages Our setting: MI, Batch, Dynamically typed

Compressing the Dispatching Matrix n Dispatching matrix Duplicates elimination vs. Null elimination l is usually 10 times smaller than w n Problem parameters: n n = # types = 10 n m = # different messages = 12 n l = # method implementations = 27 n w = # non-null entries = 46

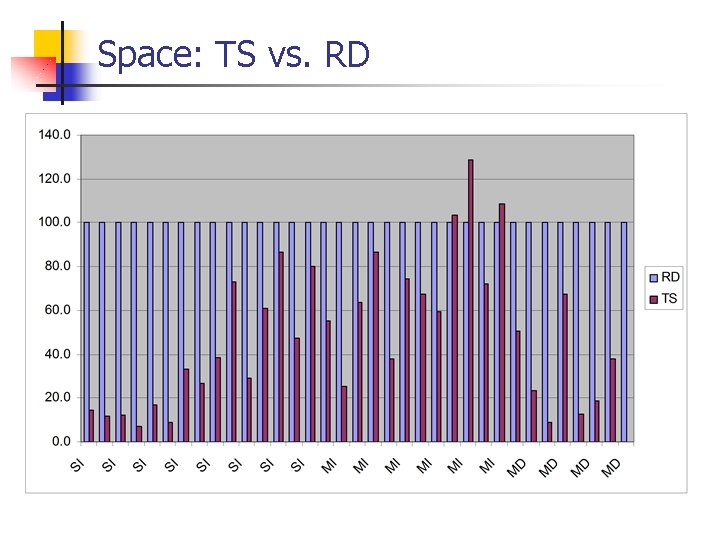
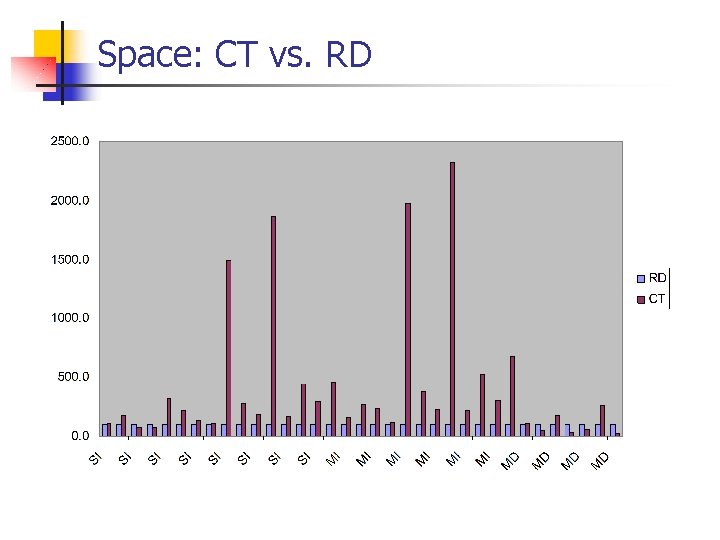
Previous Work n Null elimination n Virtual Function Tables (VFT) n n n Selector Coloring (SC) [Dixon et al. '89] Row Displacement (RD) [Driesen '93, '95] n n n Only for statically typed languages In SI: Optimal null elimination In MI: tightly coupled with C++ object model. Empirically, RD comes close to optimal null elimination (1. 06 • w) Slow creation time Duplicates elimination n n Compact dispatch Tables (CT) [Vitek & Horspool '94, '96] Interval Containment, only for single inheritance (SI) n Linear space and logarithmic dispatch time

Row Displacement (RD) n Displace the rows/columns of the dispatching matrix by different offsets, and collapse them into a master array. Dispatching matrix with a new type ordering The columns with different offsets The master array

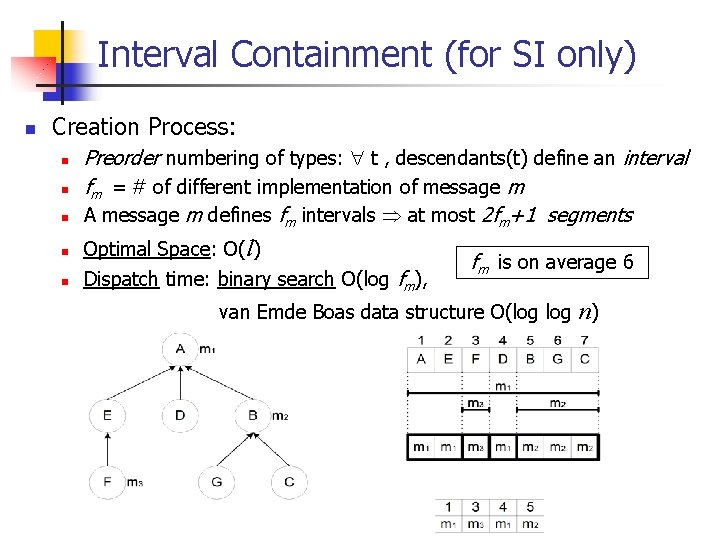
Interval Containment (for SI only) n Creation Process: n Preorder numbering of types: t , descendants(t) define an interval fm = # of different implementation of message m A message m defines fm intervals at most 2 fm+1 segments n Optimal Space: O(l) n Dispatch time: binary search O(log fm), n n fm is on average 6 van Emde Boas data structure O(log n)

Our Technique: Type Slicing (TS) n n n Generalizes Interval Containment Idea (more details later) Partition the hierarchy into n Apply interval containment in each slice n Retrieve the slice of the receiver Jump to the appropriate Interval Containment procedure n n n slices Dispatch process: n n k n For example, a binary search in logarithmic time Space: O(k l) Median value of k is 6. 5; average is 7. 3; maximum is 19 In practice, the space is much smaller (next slides)

Data-set n Large hierarchies used in real life programs k tends to be small n Greatly resemble trees n 35 hierarchies totaling 63, 972 types n n n 16 single inheritance (SI) hierarchies with 29, 162 types 12 multiple inheritance (MI) hierarchies with 27, 728 types 7 multiple dispatch hierarchies with 7, 082 types Degenerate (singleton) method families removed Properties: n n Average number of methods in a type 6. 5 Average fm 5. 9 ( 3 conditionals) Null elimination compression factor 21. 6 Duplicates elimination compression factor 203. 7

Space in SI hierarchies

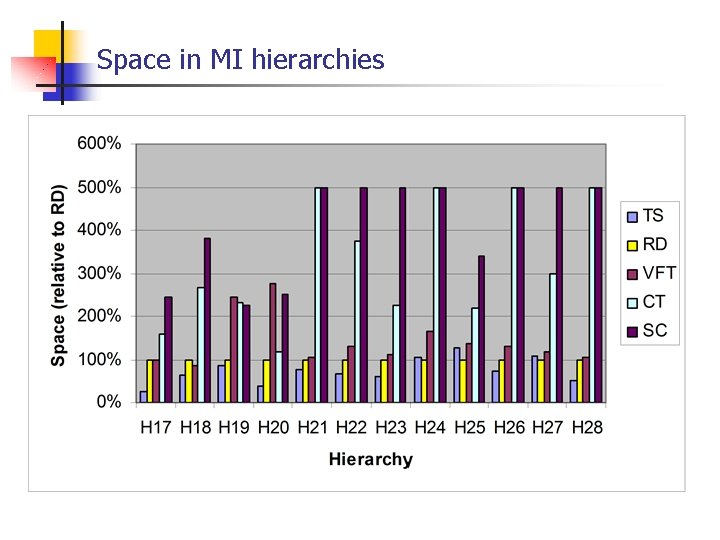
Space in MI hierarchies

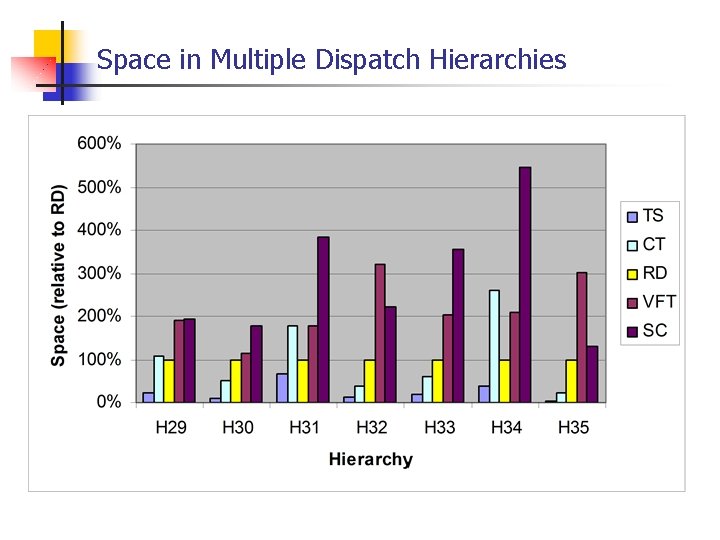
Space in Multiple Dispatch Hierarchies

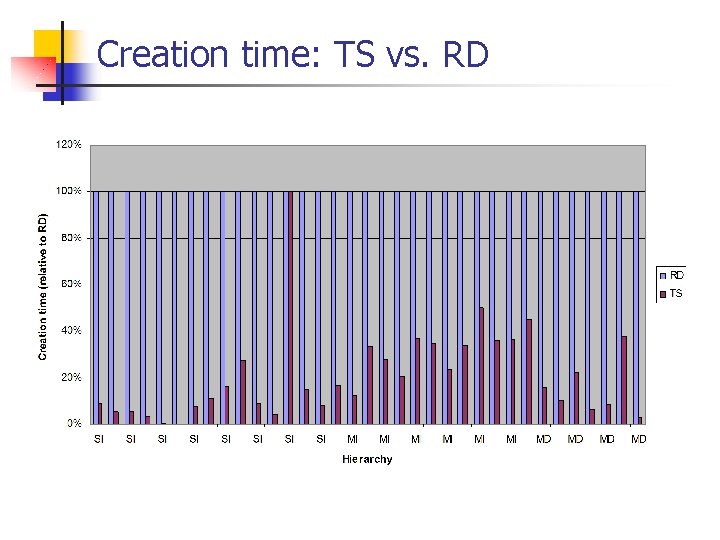
Creation time: TS vs. RD

Dispatching using a binary search n Dispatch time (in TS) n n Small. Eiffel compiler, OOPSLA’ 97: Zendra et al. n n 0. 6 ≤ average #conditionals ≤ 3. 4; Median = 2. 5 Binary search over x possible outcomes Inline the search code When x 50: binary search wins over VFT Used in previous work n OOPSLA’ 01: Alpern et al. Jalapeño – IBM JVM implementation n OOPSLA’ 99: Chambers and Chen Multiple and predicate dispatching n ECOOP’ 91: Hölzle, Chambers, and Ungar Polymorphic inline caches

The Type Slicing Technique n n In SI: descendants of t are consecutive in a preorder of the hierarchy In MI: we cannot make all descendants of t consecutive, for example: Partition the types in T into disjoint slices T 1 … Tk Find an ordering for each of the slices Slicing property: Descendants of t in each slice are consecutive in the ordering of that slice

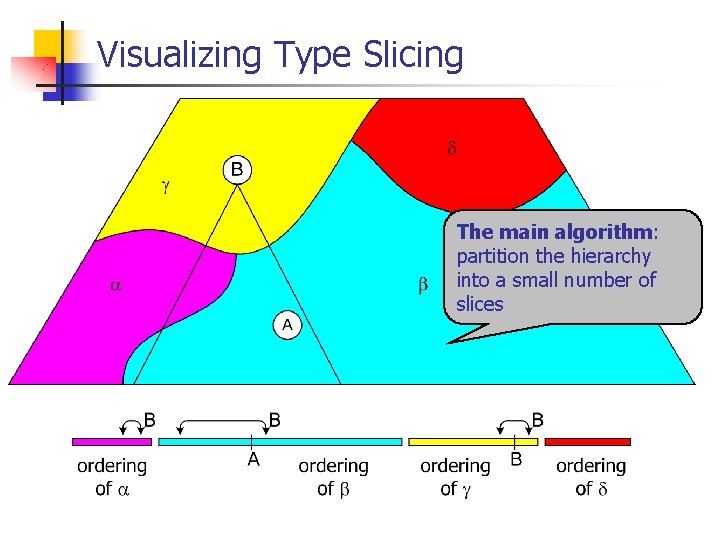
Visualizing Type Slicing The main algorithm: partition the hierarchy into a small number of slices

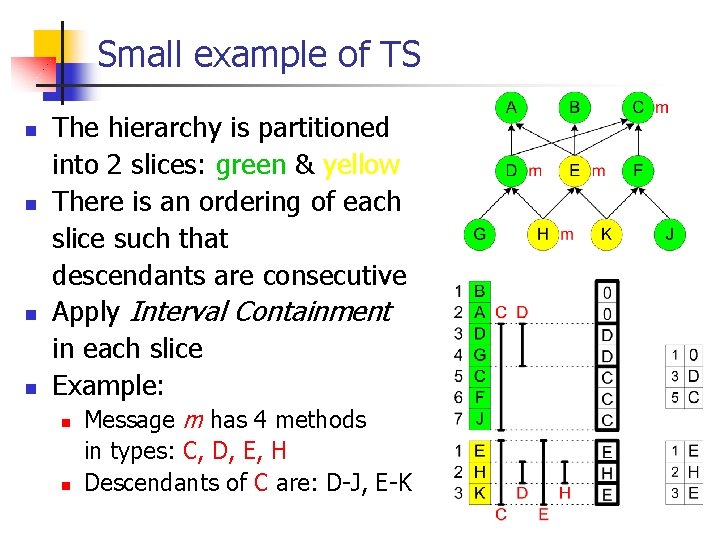
Small example of TS n n The hierarchy is partitioned into 2 slices: green & yellow There is an ordering of each slice such that descendants are consecutive Apply Interval Containment in each slice Example: n n Message m has 4 methods in types: C, D, E, H Descendants of C are: D-J, E-K

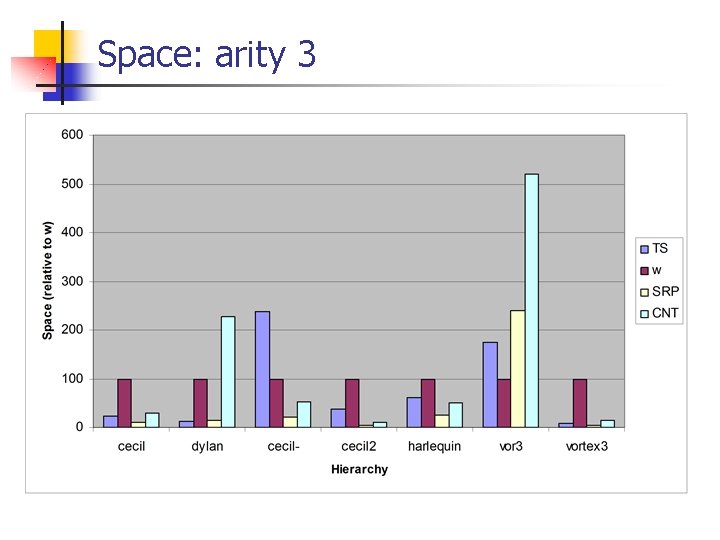
Multiple Dispatching n Dispatching over several arguments n n n Mono-dispatch stage n n n Useful, e. g. , drawing a shape over some canvas Huge space required since the dispatching matrix is multi -dimensional c regular dispatching queries for a multi-method whose arity is c We compare TS with optimal null elimination (w) Resolution stage n Using other, specialized techniques (SRP or CNT)

Conclusions & Future Research n n n TS improves the space and creation time of RD Dispatch: binary search rather than array lookups Future work n Exploring the dynamic model n n Explore Linearizations to solve ambiguities n n n Allow insertion of types (along with their accompanying methods) as leaves (Journal version) Allow insertion of methods to existing types Allow deletions Mainly in dynamically typed languages Also appears in exception handling Constant time dispatching scheme (POPL’ 03)

The End n Any questions?

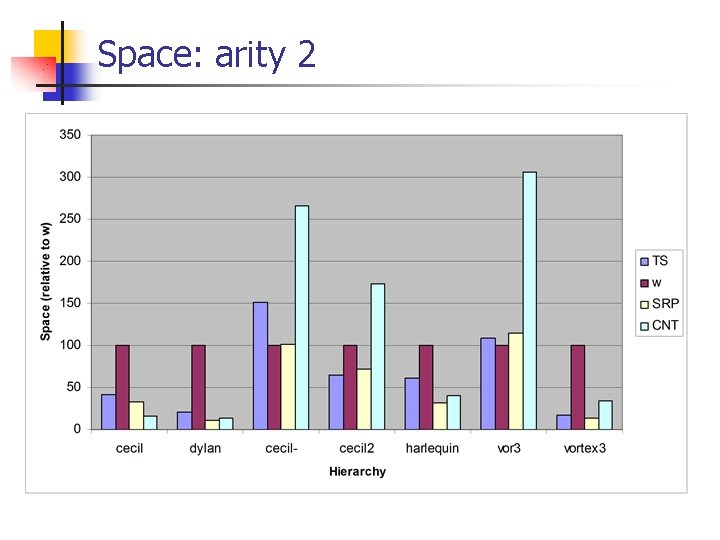
Space: arity 2

Space: arity 3

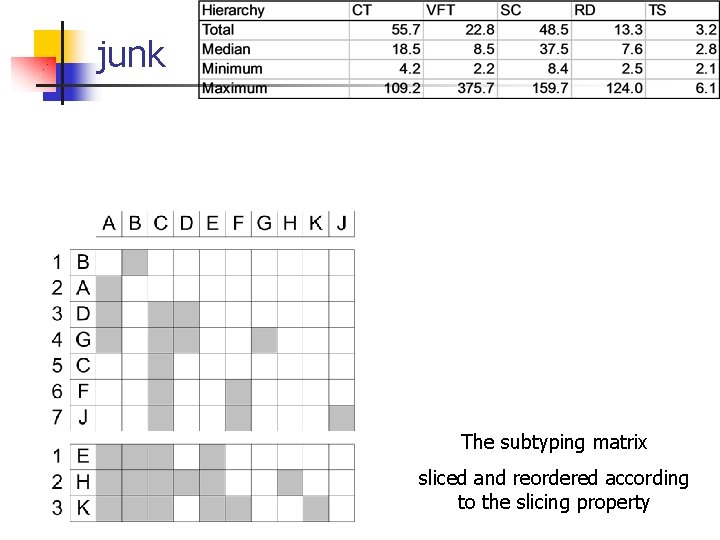
junk The subtyping matrix sliced and reordered according to the slicing property

Outline n n n The dispatching problem Previous work Type Slicing Results Multiple Dispatching Conclusions & Future Research

Selector Coloring (SC) n Partition the messages into the smallest number of slices n Two messages in a slice do not have a type which recognizes both The eight slices of the dispatching matrix SC representation

Space: TS vs. RD

Space: CT vs. RD

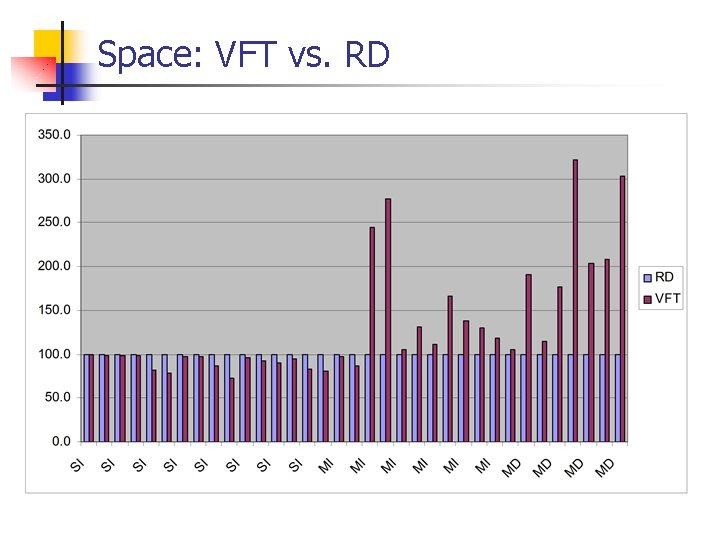
Space: VFT vs. RD

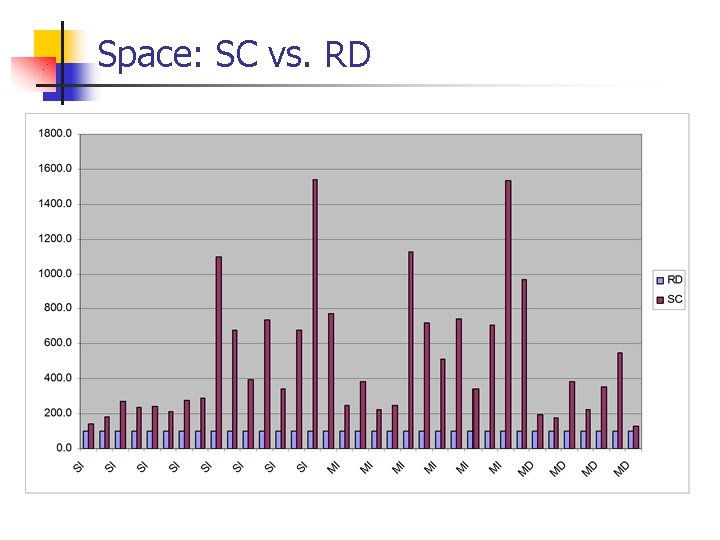
Space: SC vs. RD

Multiple Dispatching n Dispatching over several arguments Mono-dispatch stage n Resolution stage n CNT SRP

Practical techniques: CNT & SRP n n n Given a call m(a, b) Mono-dispatch stage n T 1 = L. C. A of all results of m(a, ? ) n T 2 = L. C. A of all results of m(? , b) Resolution stage n SRP n n S 1 = all relevant implementation under T 1 S 2 = all relevant implementation under T 2 Compute S 1 S 2 in a bitvector implementation CNT n Multi-dispatch in T 1 x. T 2

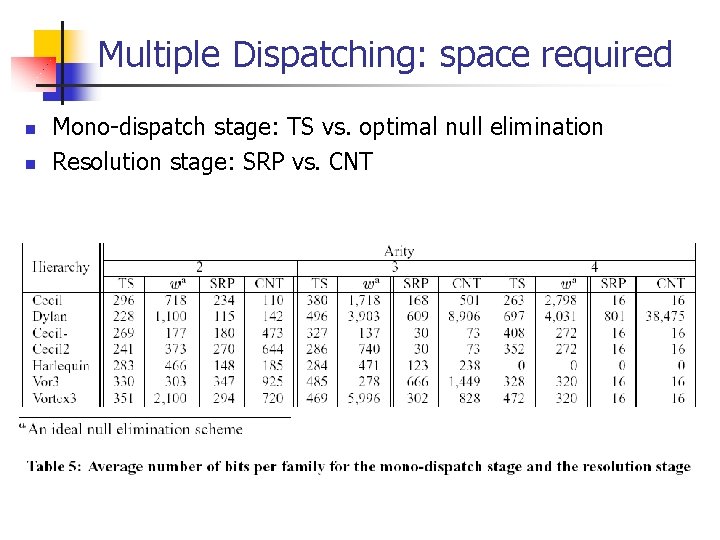
Multiple Dispatching: space required n n Mono-dispatch stage: TS vs. optimal null elimination Resolution stage: SRP vs. CNT