Fast Additive Constant Approximation Algorithms for Safe Deposit

Fast Additive Constant Approximation Algorithms for Safe Deposit Boxes problem in 2 D and 3 D. • Boaz Ben-Moshe • Yefim Dinitz

Safe Deposit Boxes problem • Given: a set S of n safe boxes, where the i-th box contains ai Dollars, bi Francs, etc. and numbers (restrictions constrains): A, B, etc. • We wish to find the minimal subset of S, such that the total Dollar value is at least A, Franc value at least B, etc. • A variant of the knapsack problem, with a fixed cost (of 1) of taking any item.

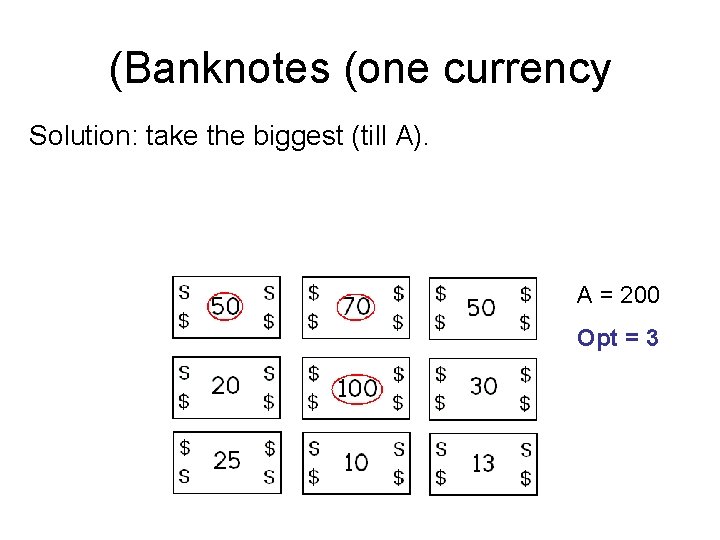
(Banknotes (one currency There are banknotes, seen on the table. We would like to take the smallest amount of banknotes, which sums up to at least A. A = 200

(Banknotes (one currency Solution: take the biggest (till A). A = 200 Opt = 3

Two currencies: Motivation Shortest link path: Given a set (V) of 2 D vectors, find the smallest subset of V, that performs a path from “start” into the half open rectangle “end”. What may be a strategy?

Two currencies: Motivation Killing processes problems: Given a set S of processes find the smallest subset of S, such that: Killing these processes, by OS, will free at least A cpu and B space. 6 9/18/2020

The state and results • Safe Deposit Box problem (SDB) is NPhard, beginning from the case of two currencies [DK]. • There is a polynomial approximation solution with a constant additive error [DK]. • Our new algorithms lead to significant improvements of running time.

[Theorem [DK • Consider m currencies instance of SDB. • Let (a : b. . . ) be the exchange rate for each currency. The value of the i-th box, w. r. t this rate, is aai + bbi + … (in, say, CAD). For any non-degenerate instance of SDB, there exist a certain exchange rate such that the opt+(m-1) most valuable boxes forms a feasible solution.

Algorithmic proof (sketch) 9 • SDB is an ILP problem. Relax it to LP, i. e. let the variables xi be fractional, between 0 and 1. • Consider an optimal vertex of the feasible polyhedron. The value is a lower bound for ILP. • At most m variables are fractional. Round them up. The resulting solution is feasible and integer, and the error is at most m-1. • The optimum of the dual LP problem is the exchange rate as in Theorem. 9/18/2020

Running time • For any (constant) m, the running time of the algorithm of [DK] is O(nm+1). The algorithm is of the type primal-dual. • There is a specific algorithm of [DK] for the case m=2; it runs in O(n 2). • Our result for m=2: O(n 2) O(n log 2 n). • Our result for m=3: O(n 4) O(n 2 log 2 n).

Our tools (shown for m=2) • Let us normalize any rate to the form (1: b) • Given an exchange rate (1: b) we can sort the boxes according to there values. • Let #A(b) be the number of best boxes (according to the b-order) needed to reach A. Similarly for #B(b). • Obviously, max{#A, #B} is an upper bound, for the optimum (it is a feasible solution). • Main Lemma: For any rate (1: b), min{#A, #B} is a lower bound.

Lower bound proof • Obviously, the total (1: b) value of any feasible solution is at least A+b. B. • Note that min{#A, #B}-1 most valuable boxes, w. r. t. (1: b), do not reach this total value bound A+b. B. • So, no min{#A, #B}-1 other boxes do; that is, they cannot form a feasible solution, as required.

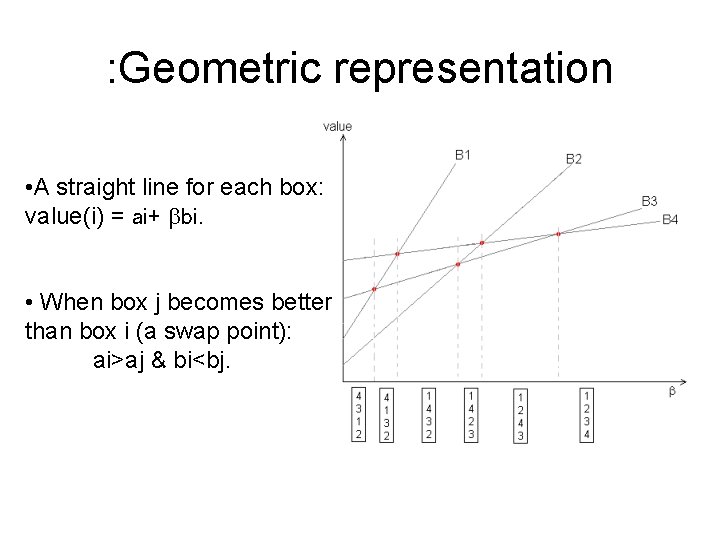
Monotonicity of #A and #B • Let us sweep b from 0 to ∞, and trace changes in the box order. • When two box values become equal, value(i)=value(j), so that before that, box i was better, and after that, box j is better, then holds ai>aj and bi<bj. • Assume General Position (for now).

: Geometric representation • A straight line for each box: value(i) = ai+ bbi. • When box j becomes better than box i (a swap point): ai>aj & bi<bj.

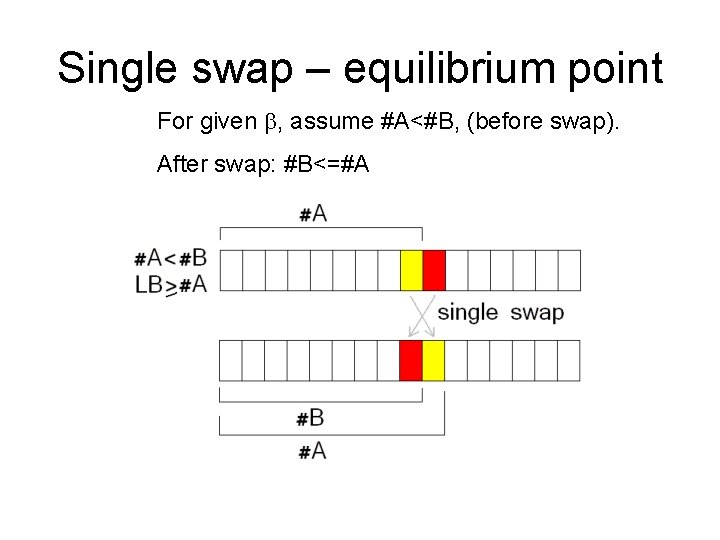
2 D Binary Search Observation: #A and #B are monotone. • Consider the equilibrium point, where a single swap turns #A=<#B into #A>=#B. • There, the lower and upper bounds for opt differ by at most one! • Thus we obtain an (opt+1) solution.

Single swap – equilibrium point For given b, assume #A<#B, (before swap). After swap: #B<=#A

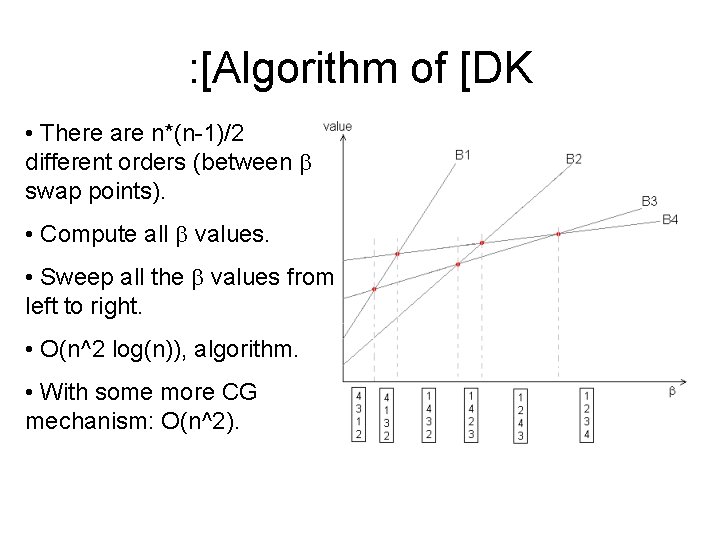
: [Algorithm of [DK • There are n*(n-1)/2 different orders (between b swap points). • Compute all b values. • Sweep all the b values from left to right. • O(n^2 log(n)), algorithm. • With some more CG mechanism: O(n^2).

…If only we could • Avoid computing all O(n 2) b values. • Use the convex (monotone) property to find the equilibrium point. • Perform binary search over b values (sorted by the x coordinate). • Introducing Slope Selection!

Slope selection • Parametric search: known (CG) technique: [Megiddo 83], [Cole 89], [Katz & Sharir 93]. • Given a set of n straight lines, the k’th intersection (sorted by x), can be found in O(n*log(n)) run time. • We use this algorithm as a “black box”.

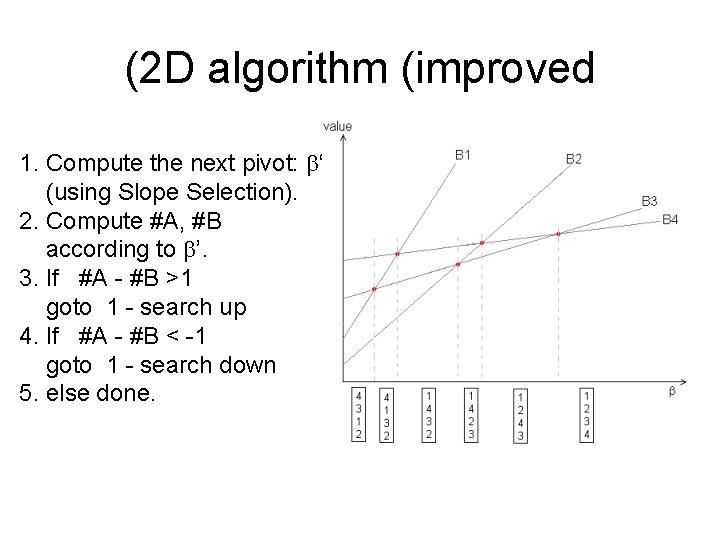
(2 D algorithm (improved 1. Compute the next pivot: b‘ (using Slope Selection). 2. Compute #A, #B according to b’. 3. If #A - #B >1 goto 1 - search up 4. If #A - #B < -1 goto 1 - search down 5. else done.

(Results (general position • Running time: – Finding the next b: O(n*log(n)). – Computing #A, #B for given b: O(n*log(n)). – Binary search steps: O(log(n)). – Total time: O(n*log^2(n)).

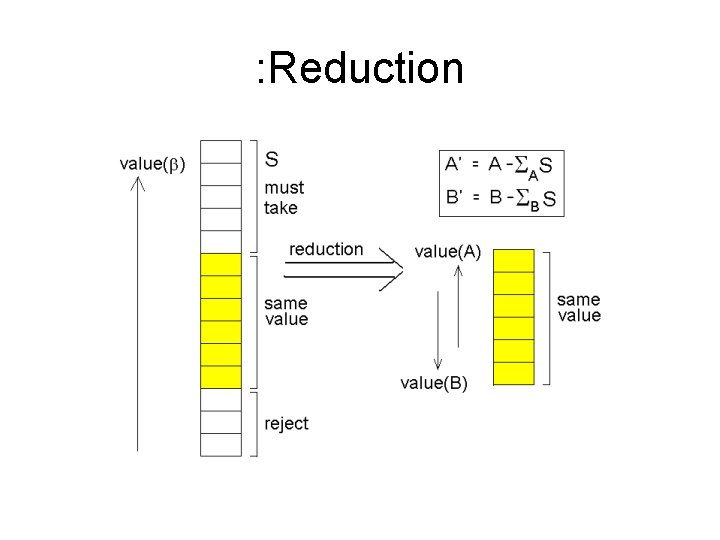
Degenerate case • Breaking “symmetric” inputs. • What if 3 boxes (lines) intersect at the same point? • Reduction to a combinatorial problem.

: Reduction

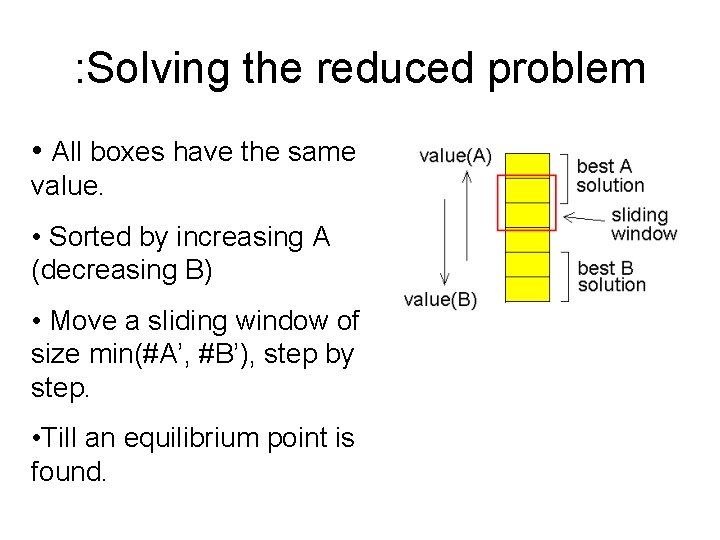
: Solving the reduced problem • All boxes have the same value. • Sorted by increasing A (decreasing B) • Move a sliding window of size min(#A’, #B’), step by step. • Till an equilibrium point is found.

The 2 D NP hardness • Suggestions ? ? • Tricky reduction.

The 2 D NP hardness • Reduction to perfect sum: given a set (S) on numbers and a value T is there a subset of S which sums up to A. • Spit to n (|S|) different problems: 1<k<n k’th instance: • Dollars: values: S, constraint: A. • Francs: values: {smax-si}, constraint: B = k*smax–A.

The 2 D NP hardness • If exist a k for which: the safe box optimal* solution is of size k there is a perfect sum for A (the set of Dollars). • If there is a perfect sum for A. Otherwise, the • Observe that any safe box optimal* solution must contains at least k boxes (k>=(A+B)/smax) • Therefore the safe box optimal* solution will find it …

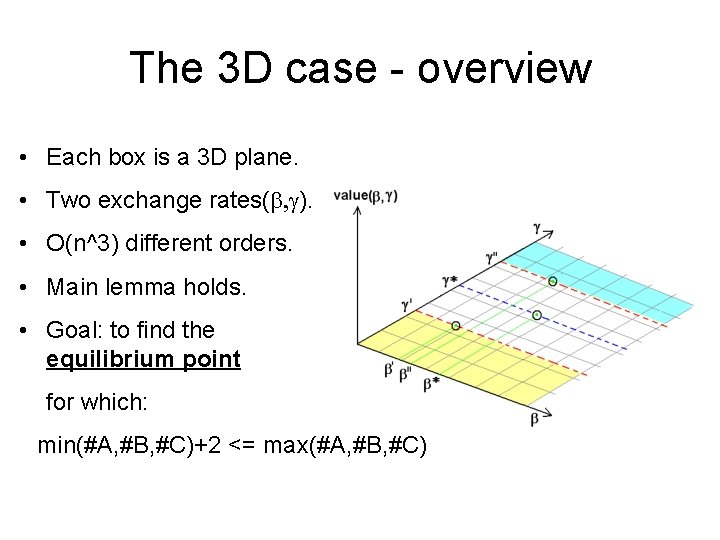
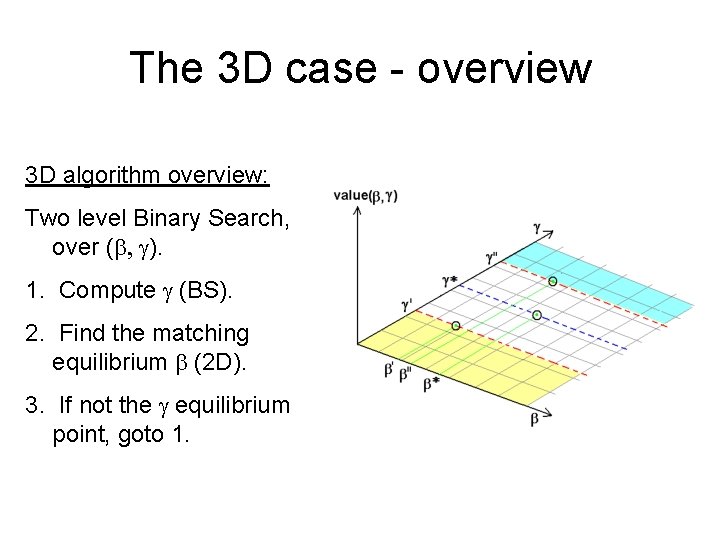
The 3 D case - overview • Each box is a 3 D plane. • Two exchange rates(b, g). • O(n^3) different orders. • Main lemma holds. • Goal: to find the equilibrium point for which: min(#A, #B, #C)+2 <= max(#A, #B, #C)

The 3 D case - overview 3 D algorithm overview: Two level Binary Search, over (b, g). 1. Compute g (BS). 2. Find the matching equilibrium b (2 D). 3. If not the g equilibrium point, goto 1.

Three currencies case Generalization to 3 D is not that obvious: • • For each fixed g, we balance not A and B currencies, but A+g. C (an artificial currency) and B - in order to maintain monotonicity. The critical lines in the (b : g) plane are the projections of the intersection lines of n planes ai+bbi+gci. searching for the equilibrium value of g. Binary search over O(n^4) g values.

Three currencies case (continued) Generalization to 3 D is not that obvious: • • Eventually, we find two neighboring values of g, where #A and #C flips (from the late to early satisfaction). However, this is not all, yet, since the A+g. C constraint is only a tool. Hence, a certain fine tuning is needed, between the above two values of g.

Running time, for three currencies • Since there are n 2 straight lines, a request to the Slope Selection method costs O(n 2 log n). • Processing of each line (g is fixed) finding the 2 D equilibrium costs O(n log^2 n). • Thus, the total time is O(n 2 log 2 n).

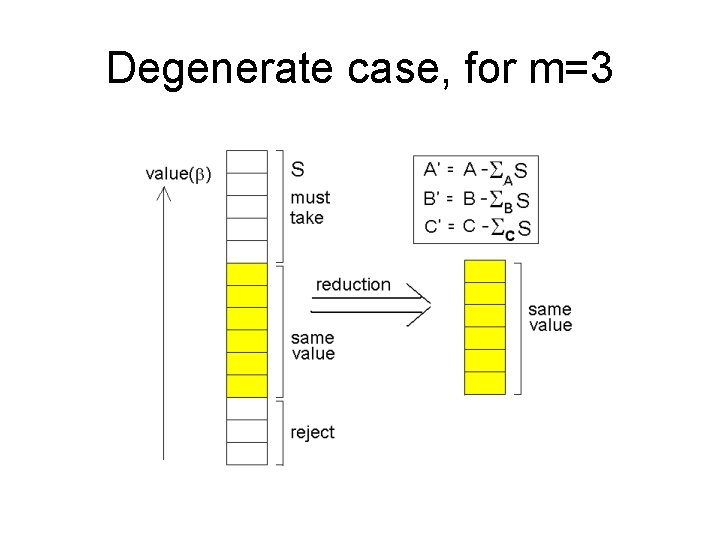
Degenerate case, for m=3

Degenerate case, for m=3 • A nice combinatorial problem arises, at the gequilibrium: All values ai+bbi+gci=V (a constant); k=(A+B+C)/V is a lower bound; We look for a feasible set of k+2 boxes. Observation: for any k boxes at least one restriction must be satisfied.

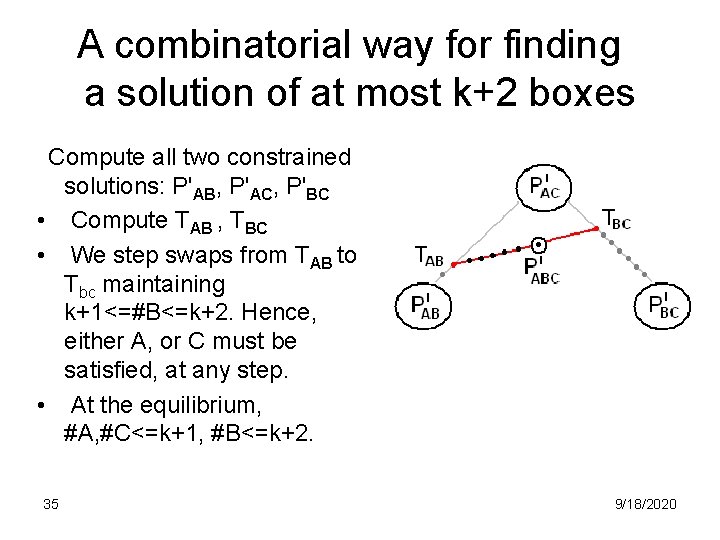
A combinatorial way for finding a solution of at most k+2 boxes Compute all two constrained solutions: P'AB, P'AC, P'BC • Compute TAB , TBC • We step swaps from TAB to Tbc maintaining k+1<=#B<=k+2. Hence, either A, or C must be satisfied, at any step. • At the equilibrium, #A, #C<=k+1, #B<=k+2. 35 9/18/2020

Possible directions of research • Parametric search ? ? : for the specific problem find b (and not k): – Open the black box: – Reducing the runtime to O(n log(n)). • Lower bound 2 D: W(n) , W(n log(n)) ? ? • Lower bound 3 D: ? – 3 sum hard?

Possible directions of research • 4 D: – Simply generalization of the 3 D method – leads to inefficient runtime (too many exchange rates) • KD: – LP approach: could the algorithm ne reduces to O(nm log…) ?

FIN • benmoshe@cs. bgu. ac. il • www. cs. bgu. ac. il/~benmoshe/PHD/safe. Box 38 9/18/2020