FAMUFSU College of Engineering EEL 3705 3705 L

FAMU-FSU College of Engineering EEL 3705 / 3705 L Digital Logic Design Spring 2007 Instructor: Dr. Michael Frank Module #14: Modular Sequential Design (Thanks to Dr. Perry for some slides)

FAMU-FSU College of Engineering Frequently-Used Modular Sequential Components o Memory elements: n n n o Flip-flops & Registers (already covered) Synchronous ROMs (w. registered I/O ports) RAMs (asynchronous & synchronous) Simple, common state machines: n n n Counters (plain binary and mod-n) Accumulators Shift registers (left/right, w. serial & parallel I/O)

FAMU-FSU College of Engineering Insert more slides here… o Most of the remaining slides in this module need to be deleted, and replaced with some slides giving examples of modular sequential designs of the above components, and explaining their functions…

FAMU-FSU College of Engineering Dr. Perry’s Slides Following are some old slides by Dr. Perry on Counters and Shift Registers, left over from previous semesters…

FSM Examples

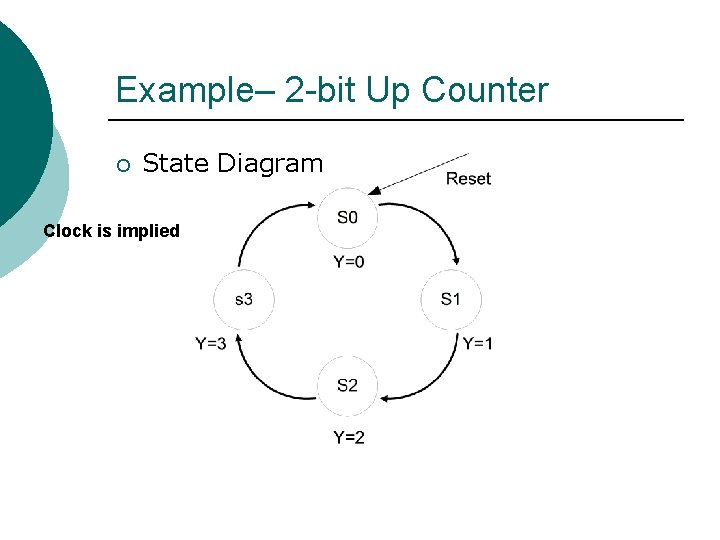
Example– 2 -bit Up Counter ¡ State Diagram Clock is implied

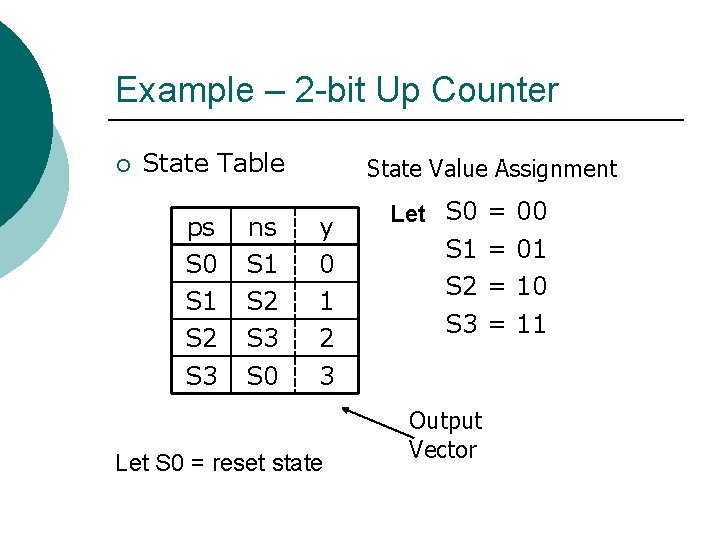
Example – 2 -bit Up Counter ¡ State Table ps S 0 S 1 S 2 S 3 ns S 1 S 2 S 3 S 0 State Value Assignment y 0 1 2 3 Let S 0 = reset state Let S 0 = 00 S 1 = 01 S 2 = 10 S 3 = 11 Output Vector

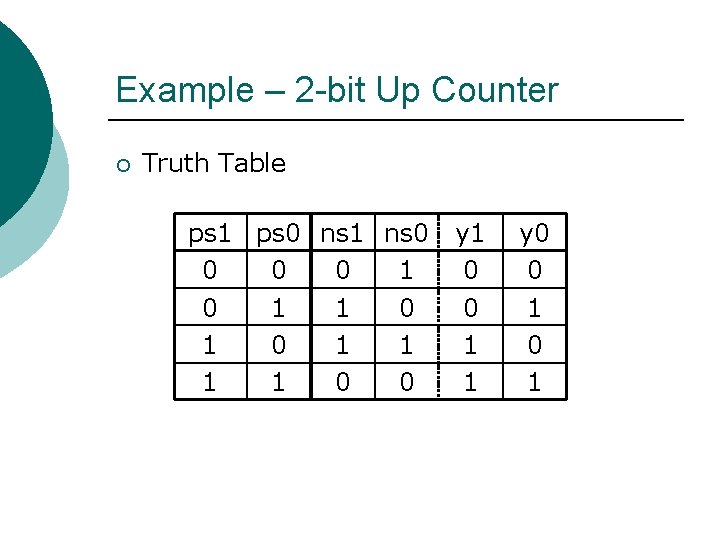
Example – 2 -bit Up Counter ¡ Truth Table ps 1 ps 0 ns 1 ns 0 0 1 0 1 0 1 1 0 0 y 1 0 0 1 1 y 0 0 1

Example – 2 -bit Up Counter ¡ Excitation Equations

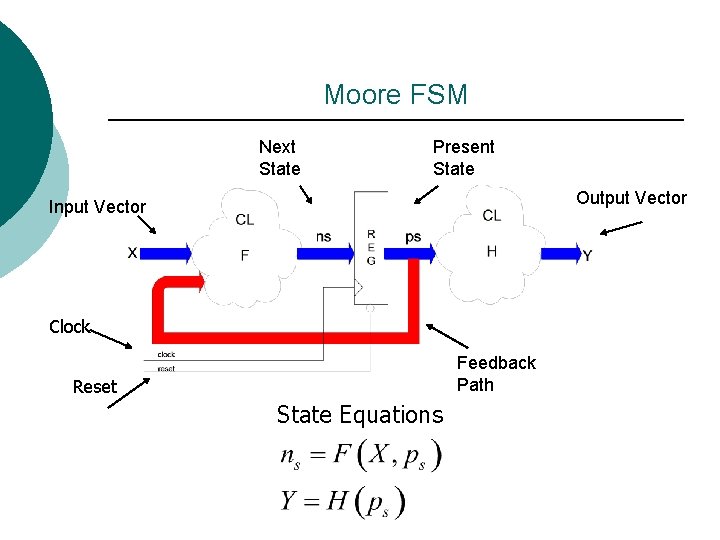
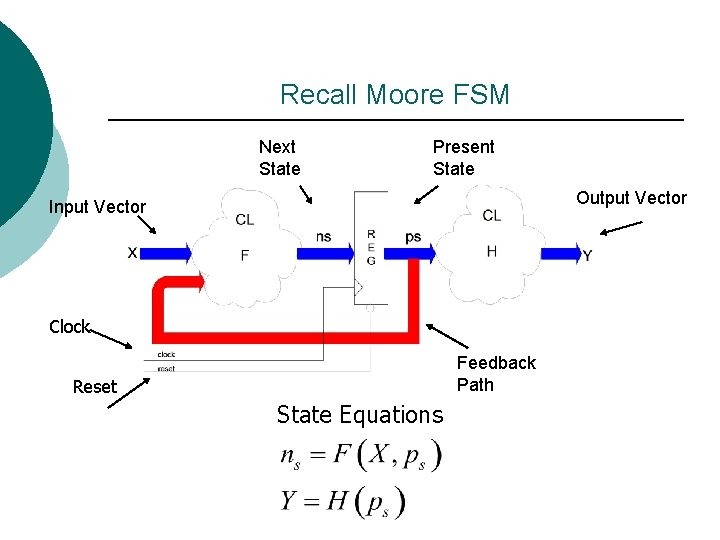
Moore FSM Next State Present State Output Vector Input Vector Clock Feedback Path Reset State Equations

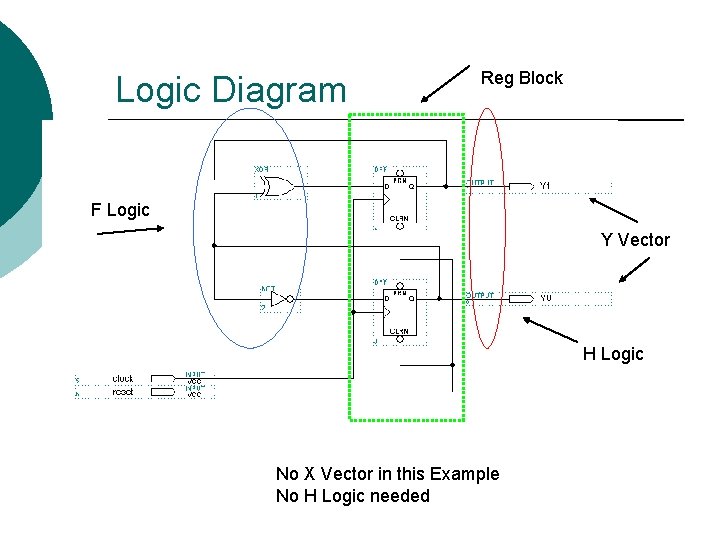
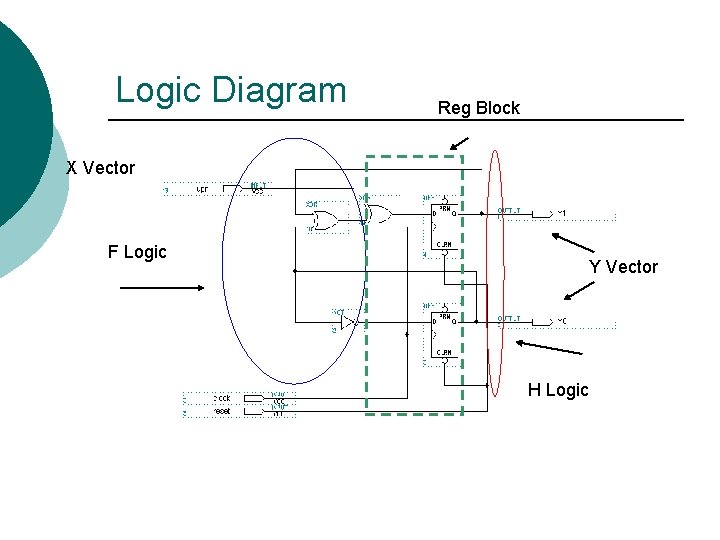
Logic Diagram Reg Block F Logic Y Vector H Logic No X Vector in this Example No H Logic needed

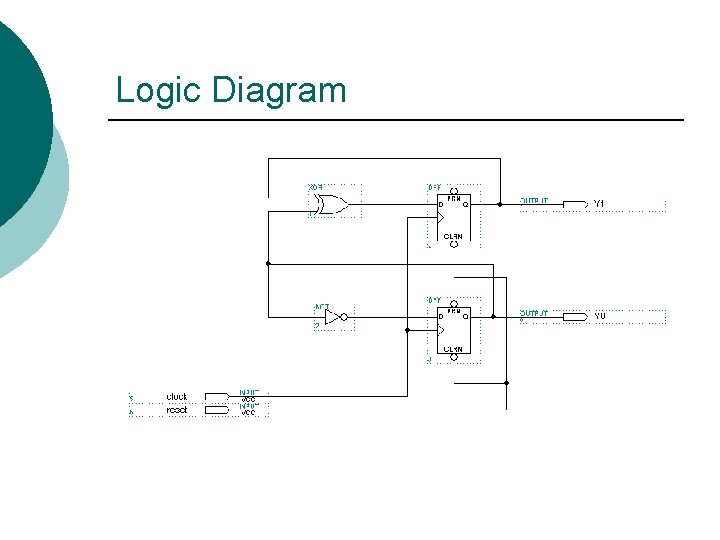
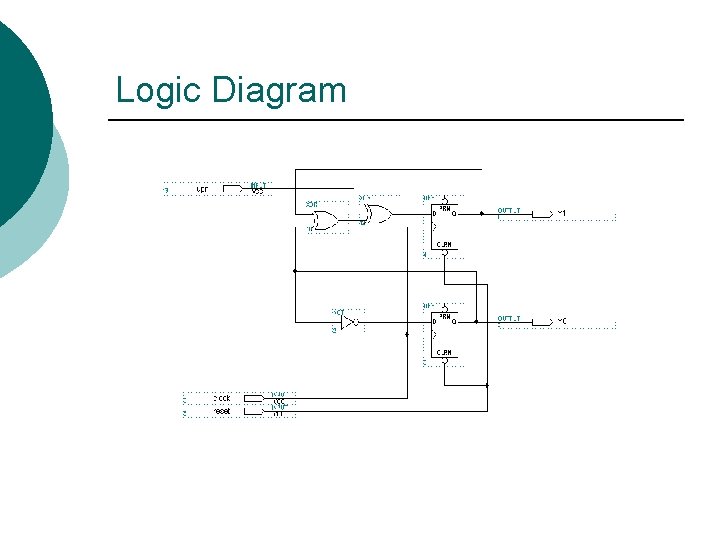
Logic Diagram

Flash Animation

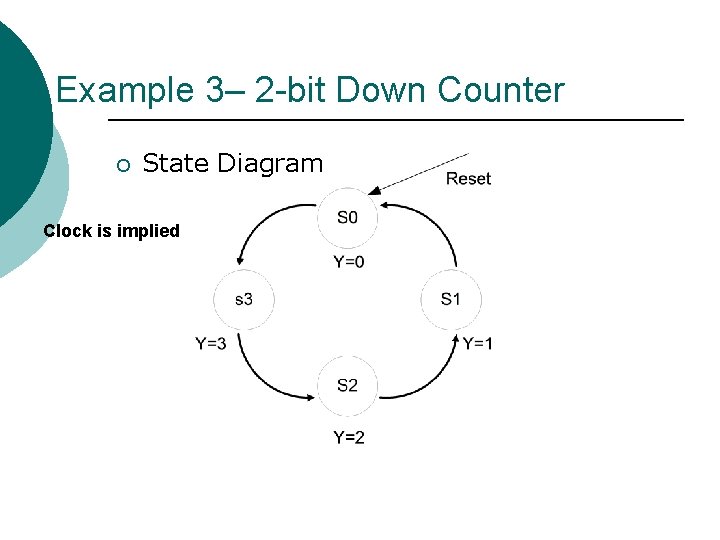
Example 3– 2 -bit Down Counter ¡ State Diagram Clock is implied

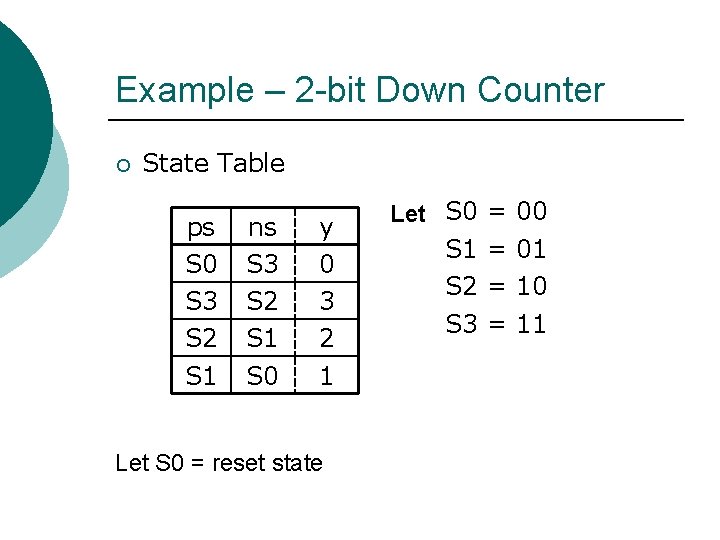
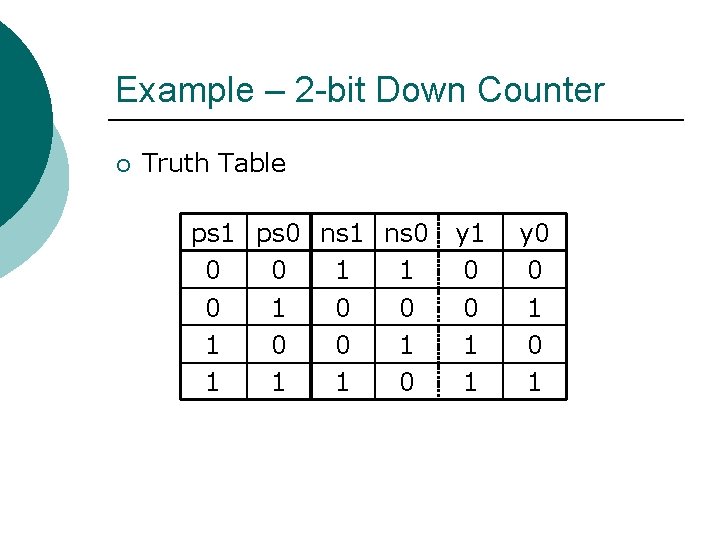
Example – 2 -bit Down Counter ¡ State Table ps S 0 S 3 S 2 S 1 ns S 3 S 2 S 1 S 0 y 0 3 2 1 Let S 0 = reset state Let S 0 = 00 S 1 = 01 S 2 = 10 S 3 = 11

Example – 2 -bit Down Counter ¡ Truth Table ps 1 ps 0 ns 1 ns 0 0 0 1 1 0 0 1 1 0 y 1 0 0 1 1 y 0 0 1

Example – 2 -bit Down Counter ¡ Excitation Equations

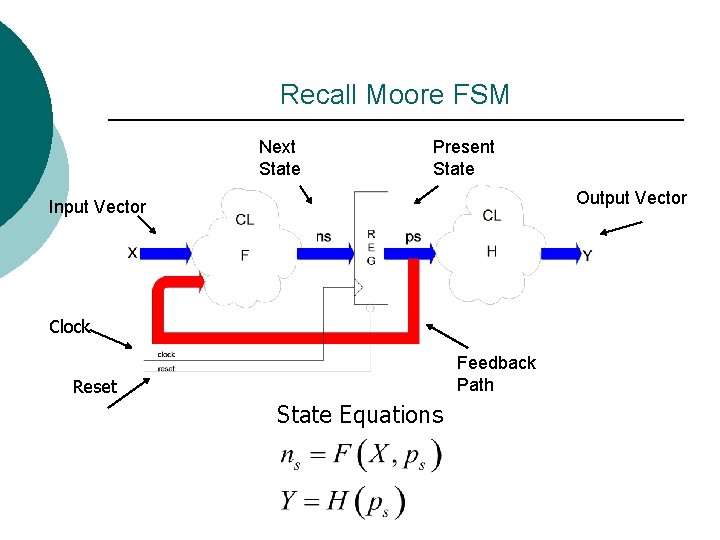
Recall Moore FSM Next State Present State Output Vector Input Vector Clock Feedback Path Reset State Equations

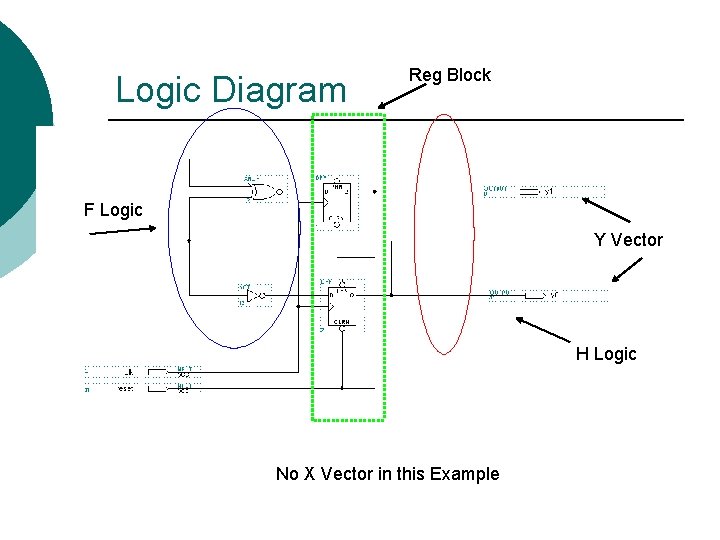
Logic Diagram Reg Block F Logic Y Vector H Logic No X Vector in this Example

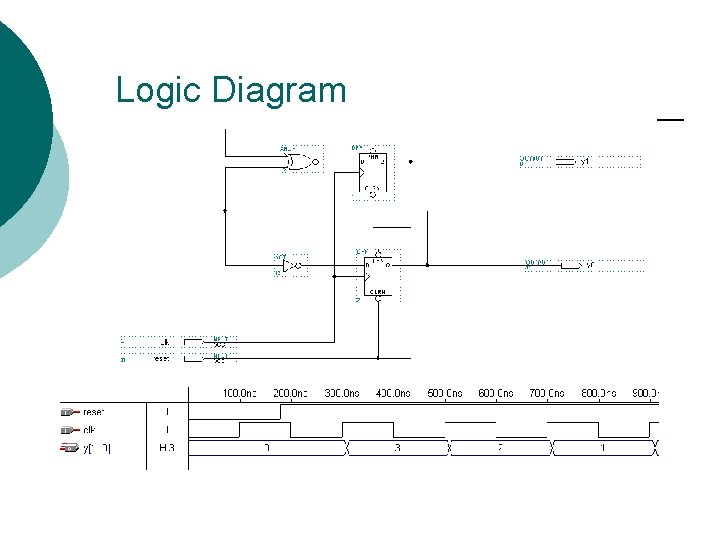
Logic Diagram

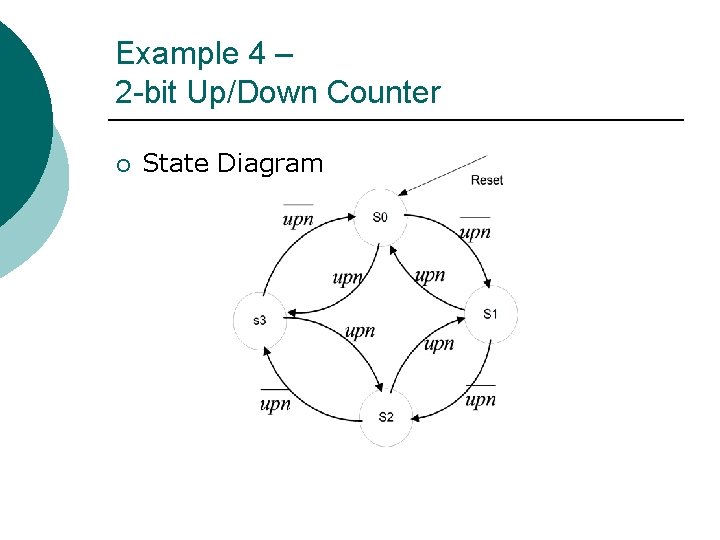
Example 4 – 2 -bit Up/Down Counter ¡ State Diagram

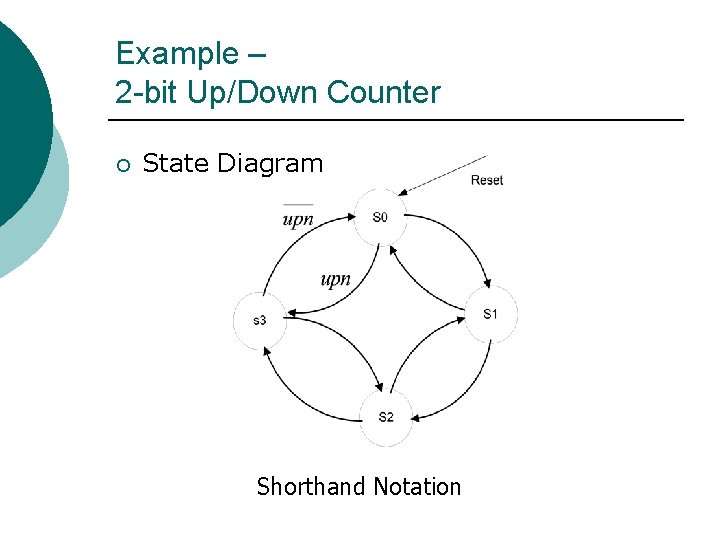
Example – 2 -bit Up/Down Counter ¡ State Diagram Shorthand Notation

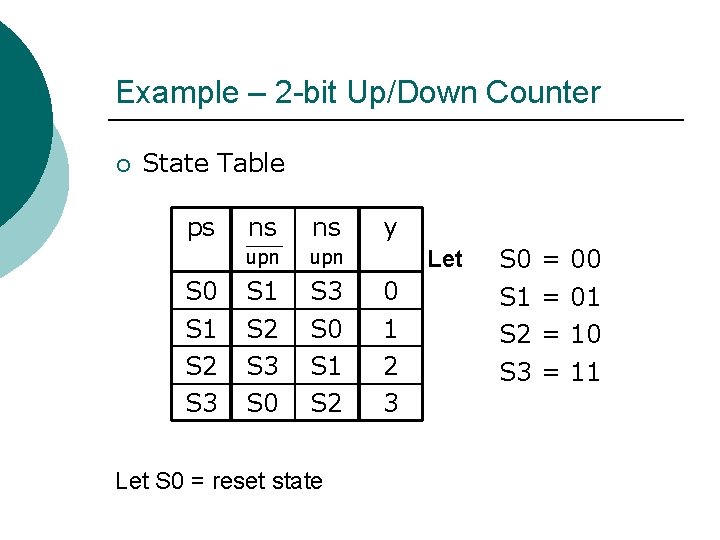
Example – 2 -bit Up/Down Counter ¡ State Table ps S 0 S 1 S 2 S 3 ns ns upn S 1 S 2 S 3 S 0 S 1 S 2 Let S 0 = reset state y Let 0 1 2 3 S 0 = 00 S 1 = 01 S 2 = 10 S 3 = 11

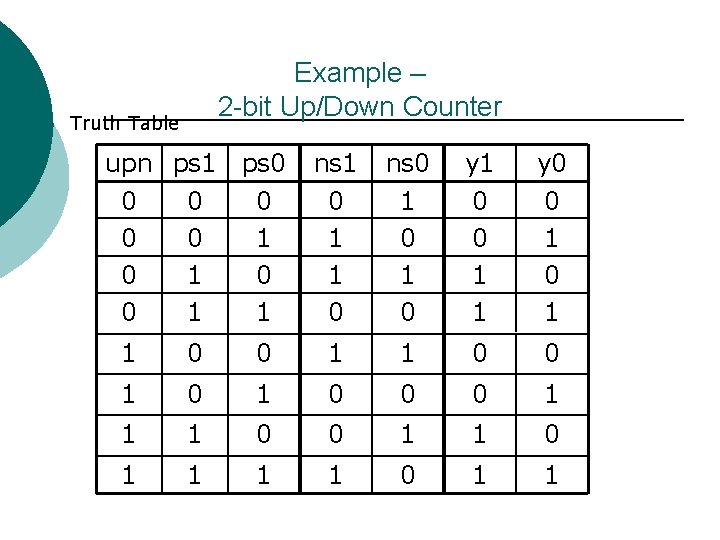
¡ Example – 2 -bit Up/Down Counter Truth Table upn ps 1 ps 0 0 0 1 1 ns 1 0 1 1 0 ns 0 1 0 y 1 0 0 1 1 y 0 0 1 1 0 0 1 0 1 0 0 0 1 1 1 1 0 1 1

Example – 2 -bit Up/Down Counter ¡ Excitation Equations

Recall Moore FSM Next State Present State Output Vector Input Vector Clock Feedback Path Reset State Equations

Logic Diagram Reg Block X Vector F Logic Y Vector H Logic

Logic Diagram

Example 5– 3 -bit Arbitrary Counter Design a 3 -bit arbitrary counter that will count in the following sequence 3, 2, 3, 1, 2, 3 If a state is not used reset it to state zero. ¡ • • • How may states do we have? How many registers do we need? How many bits do we need for Y?

Example 5– 3 -bit Arbitrary Counter ¡ State Diagram

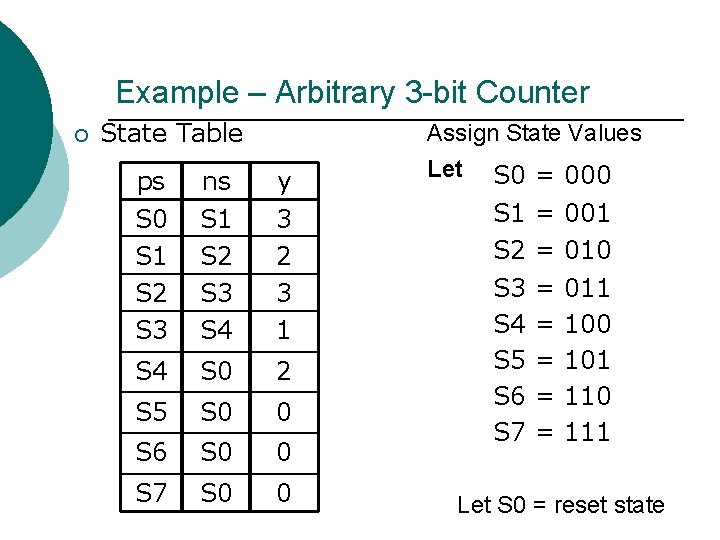
Example – Arbitrary 3 -bit Counter ¡ State Table Assign State Values ps S 0 S 1 S 2 S 3 ns S 1 S 2 S 3 S 4 y 3 2 3 1 S 4 S 0 2 S 5 S 0 0 S 6 S 0 0 S 7 S 0 0 Let S 0 = 000 S 1 = 001 S 2 = 010 S 3 S 4 S 5 S 6 S 7 = = = 011 100 101 110 111 Let S 0 = reset state

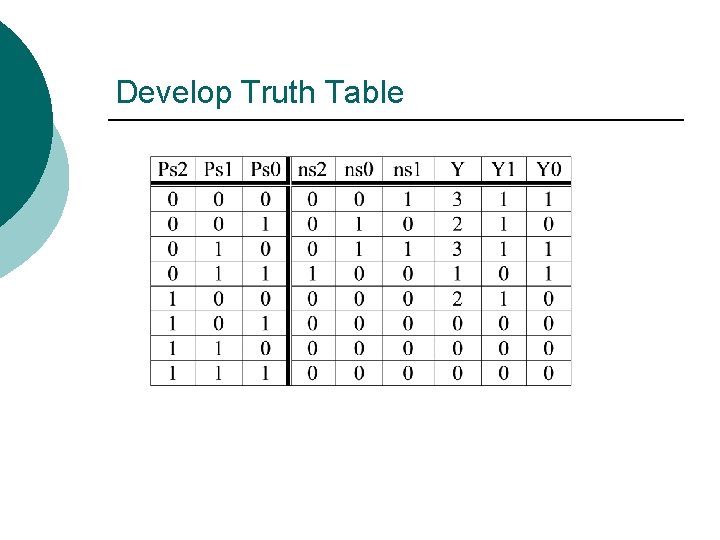
Develop Truth Table

Example – 2 -bit Arbitrary Counter ¡ Develop Excitation Equations -- F Logic

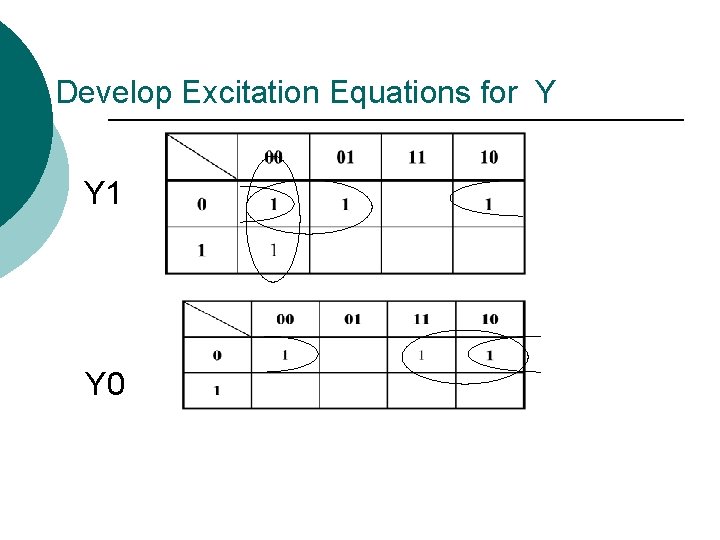
Develop Excitation Equations for Y Y 1 Y 0

Example – 2 -bit Arbitrary Counter ¡ Excitation Equations -- H Logic

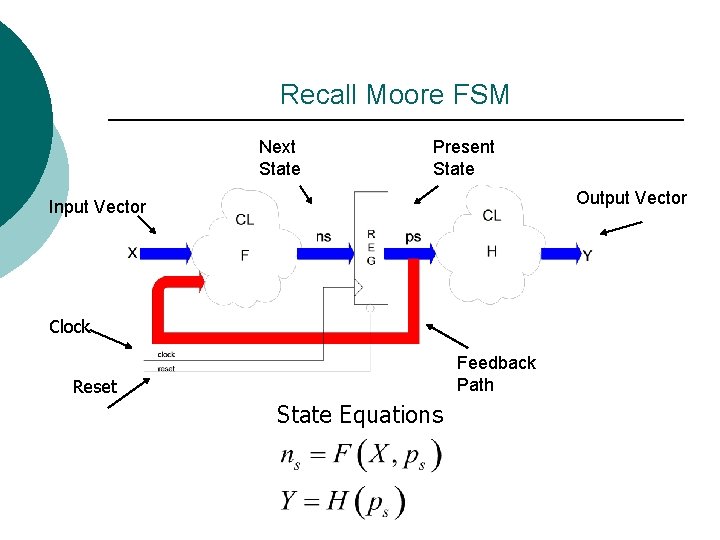
Recall Moore FSM Next State Present State Output Vector Input Vector Clock Feedback Path Reset State Equations

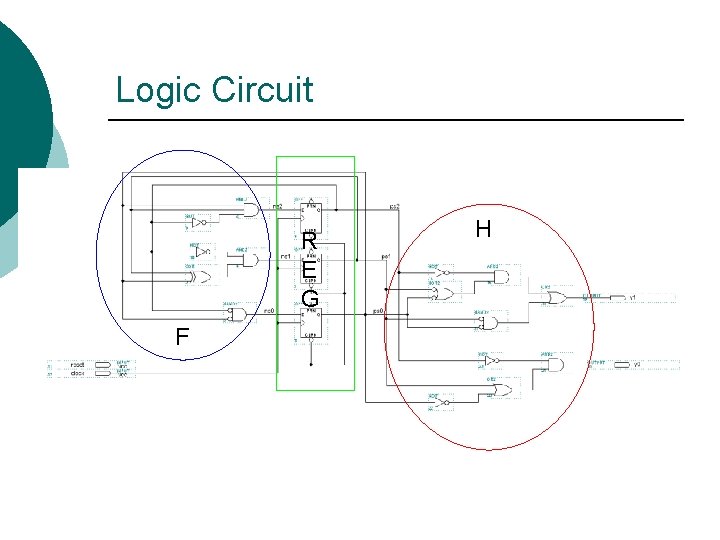
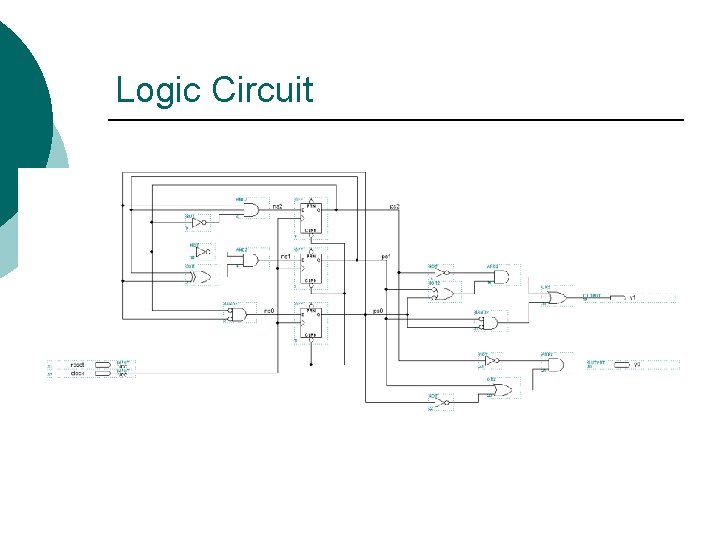
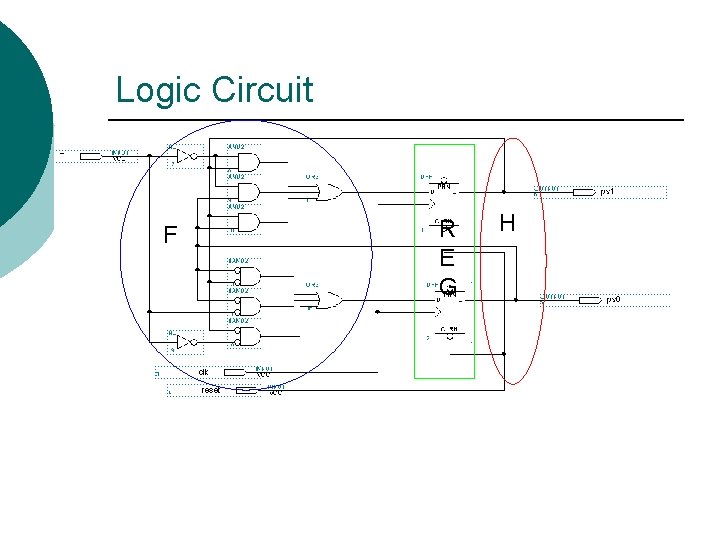
Logic Circuit R E G F H

Logic Circuit

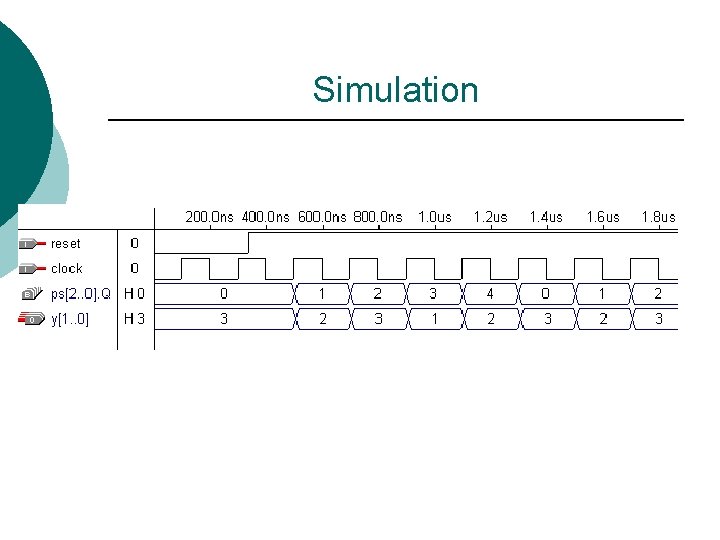
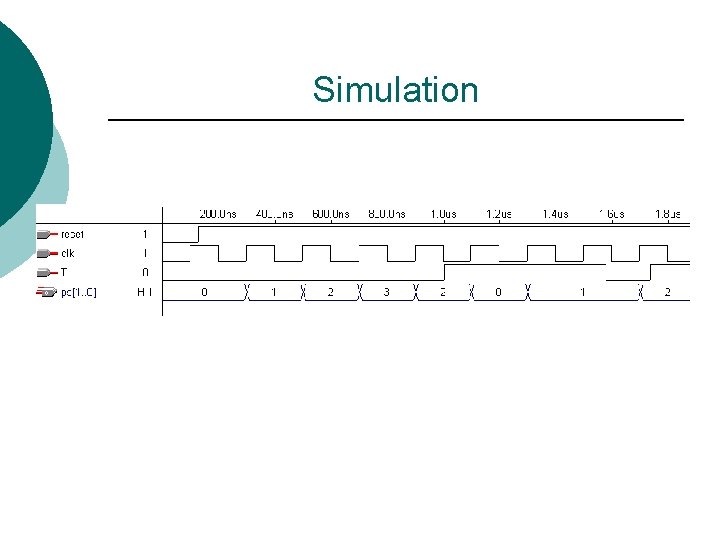
Simulation

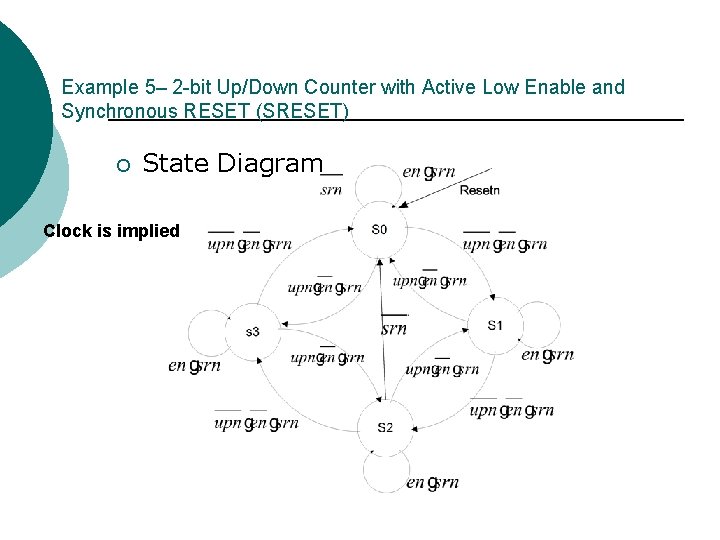
Example 5– 2 -bit Up/Down Counter with Active Low Enable and Synchronous RESET (SRESET) ¡ State Diagram Clock is implied

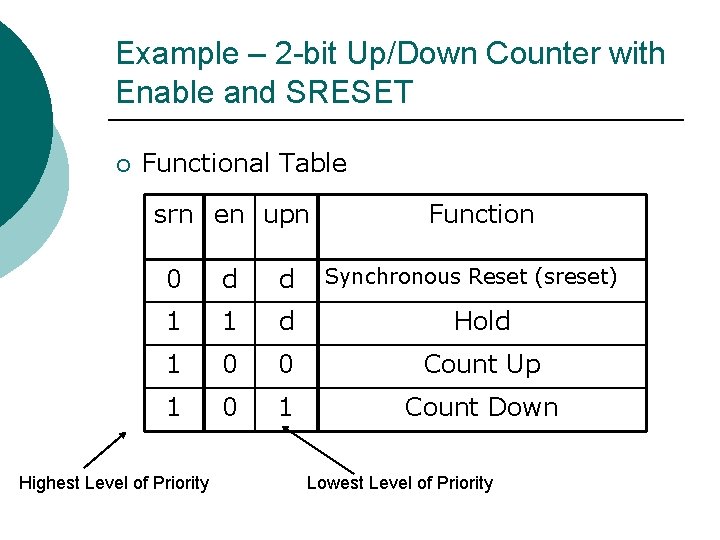
Example – 2 -bit Up/Down Counter with Enable and SRESET ¡ Functional Table srn en upn Function 0 d d 1 1 d Hold 1 0 0 Count Up 1 0 1 Count Down Highest Level of Priority Synchronous Reset (sreset) Lowest Level of Priority

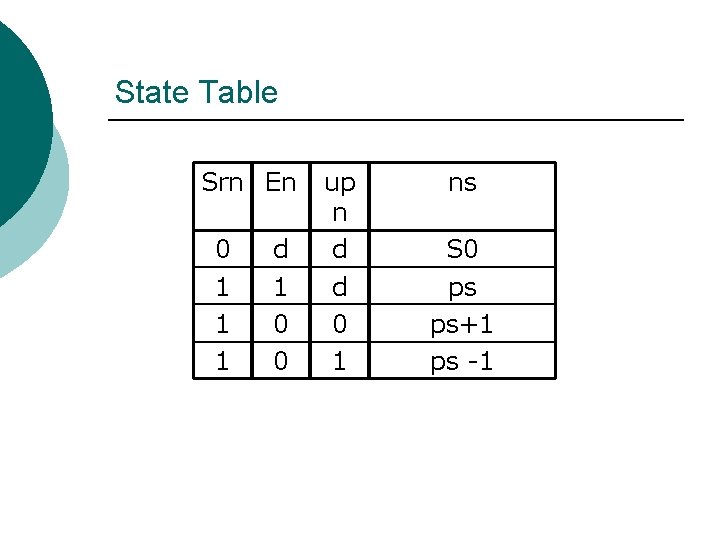
State Table Srn En 0 1 1 1 d 1 0 0 up n d d 0 1 ns S 0 ps ps+1 ps -1

Truth Table (5 variables!!) Although, we could design this circuit directly from the truth table we will use design partitioning.

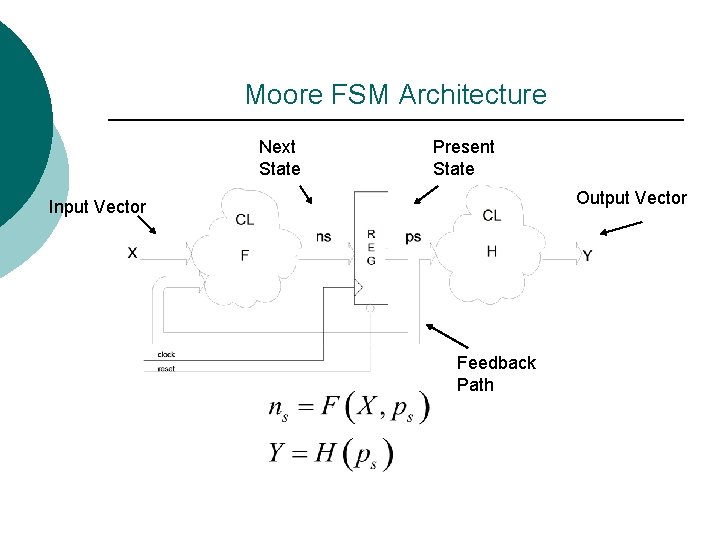
Moore FSM Architecture Next State Present State Output Vector Input Vector Feedback Path

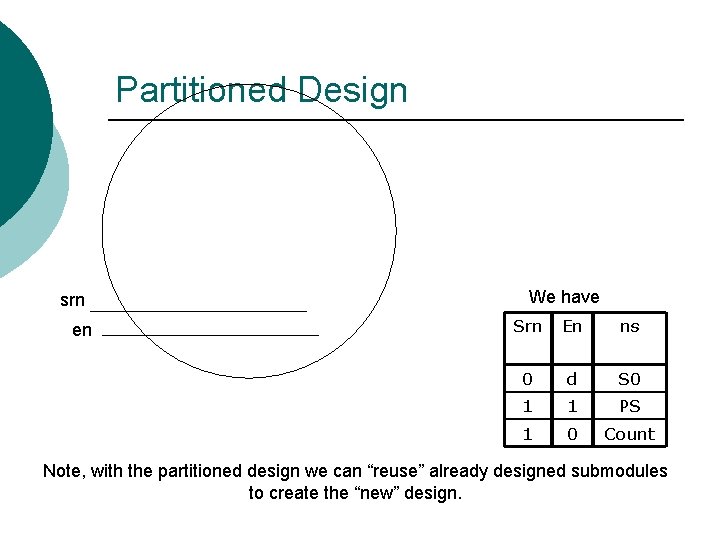
Partitioned Design srn en We have Srn En ns 0 d S 0 1 1 PS 1 0 Count Note, with the partitioned design we can “reuse” already designed submodules to create the “new” design.

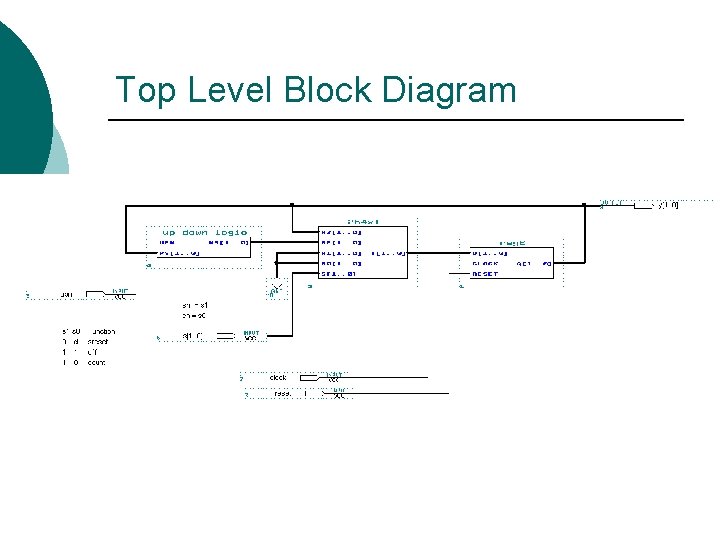
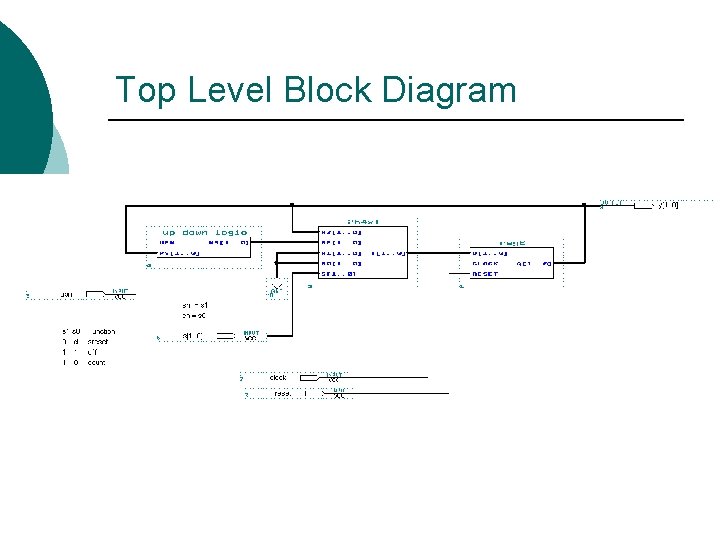
Top Level Block Diagram

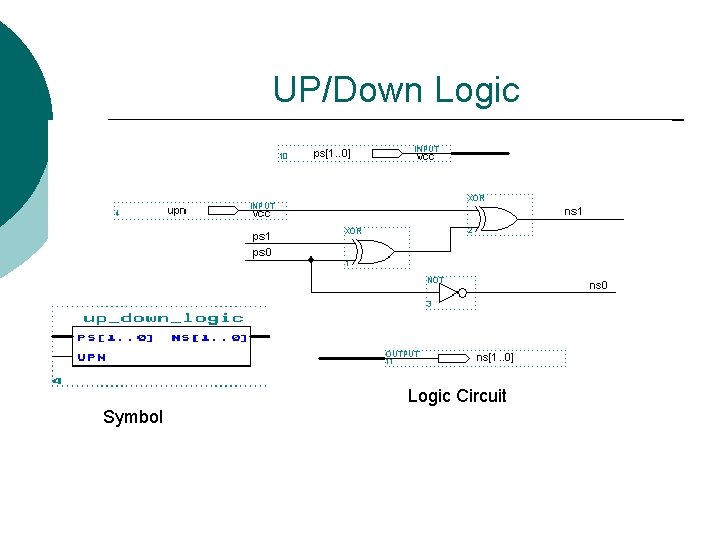
UP/Down Logic Circuit Symbol

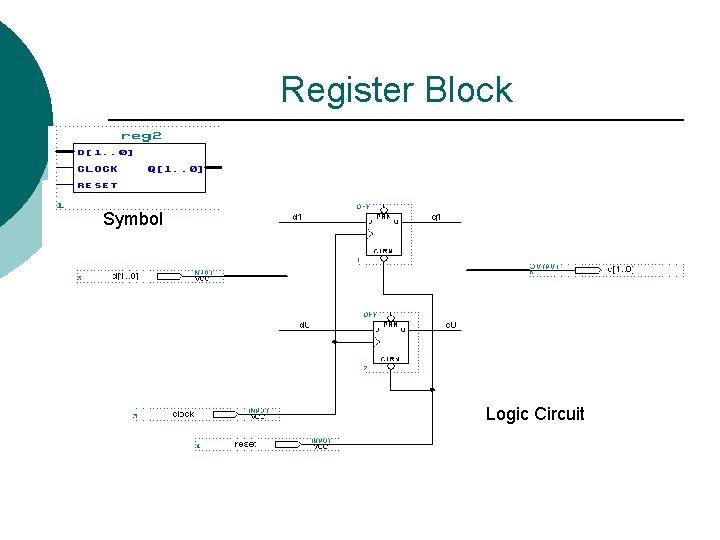
Register Block Symbol Logic Circuit

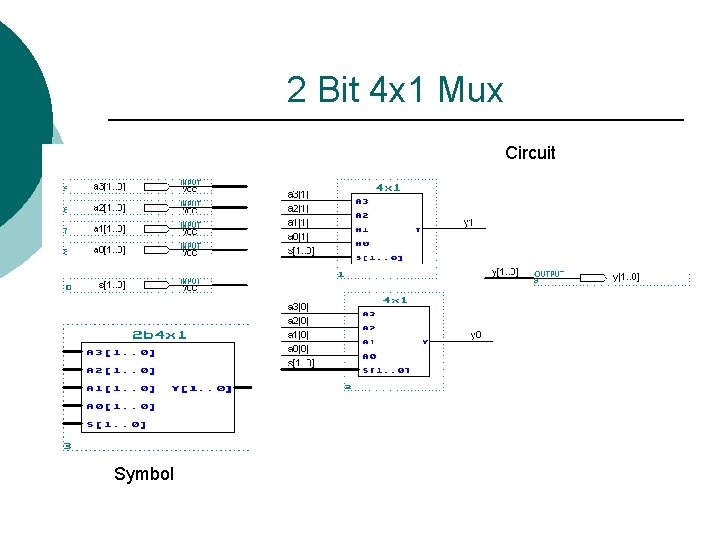
2 Bit 4 x 1 Mux Circuit Symbol

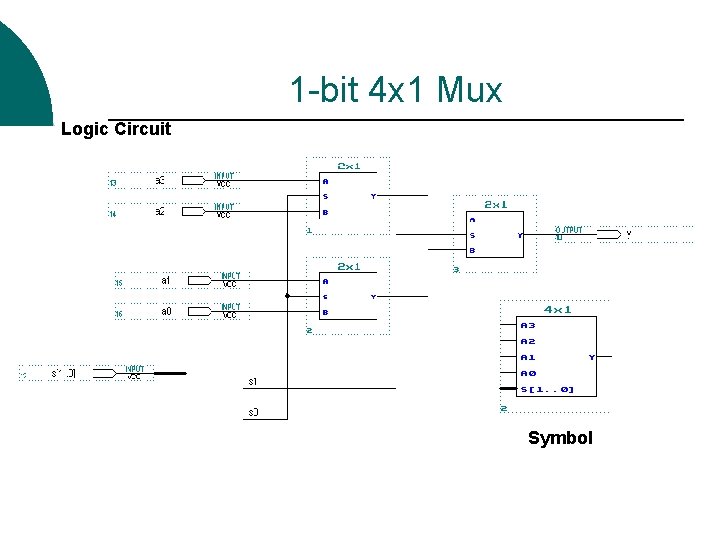
1 -bit 4 x 1 Mux Logic Circuit Symbol

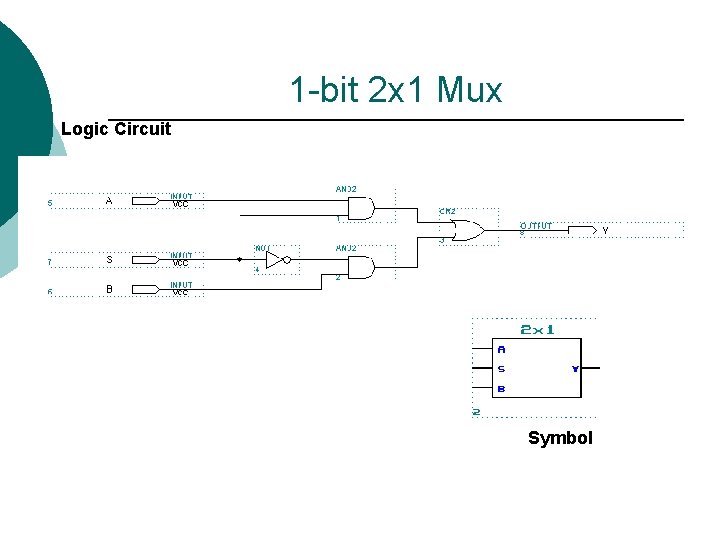
1 -bit 2 x 1 Mux Logic Circuit Symbol

Top Level Block Diagram

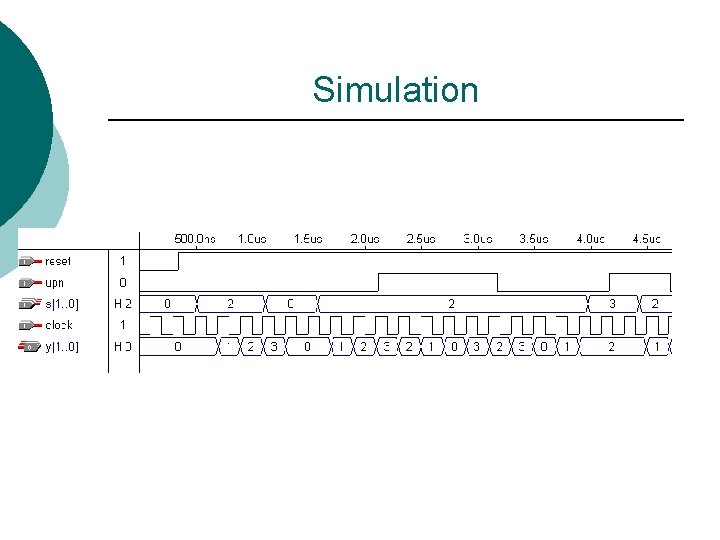
Simulation

Example 6 – FSM Controller State Diagram

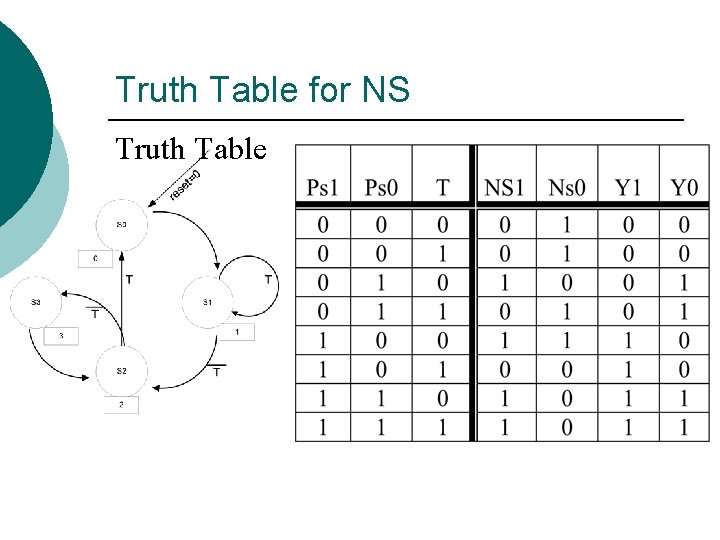
Truth Table for NS Truth Table

Kmaps for NS 1 and NS 0 NS 1 NS 0

Truth Table and Equations for Y Truth Table Recall, Moore FSM, so Y will Not be a function of T By Inspection

Logic Circuit F R E G H

Simulation

Modular Sequential Logic

Shift Registers Logic Design which manipulates the bit position of binary data by shifting it to the left or right. ¡ Major application ¡ l Serial Data to Parallel Data converters

Example ¡ Design a three-bit shift register with the following functions S 1 S 0 Function 0 0 0 1 Shift Right 1 0 Shift Left 1 1 No Shift Synchronous Reset (sreset)

Partitioned Design

No Shift Equations and Circuit

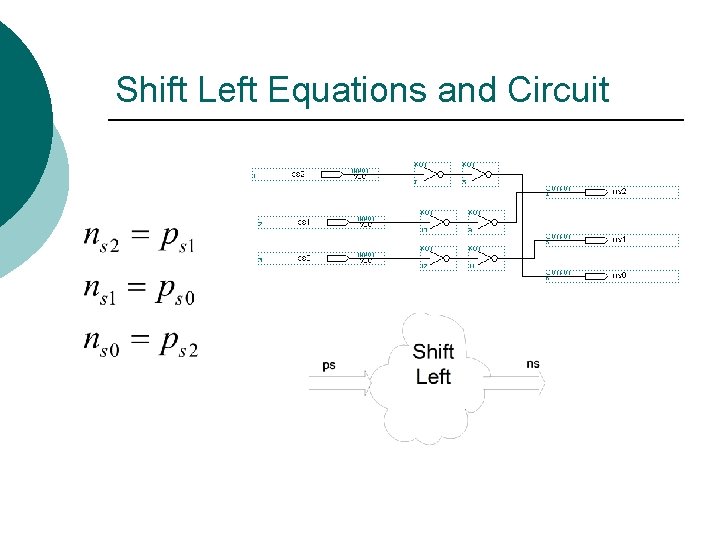
Shift Left Equations and Circuit

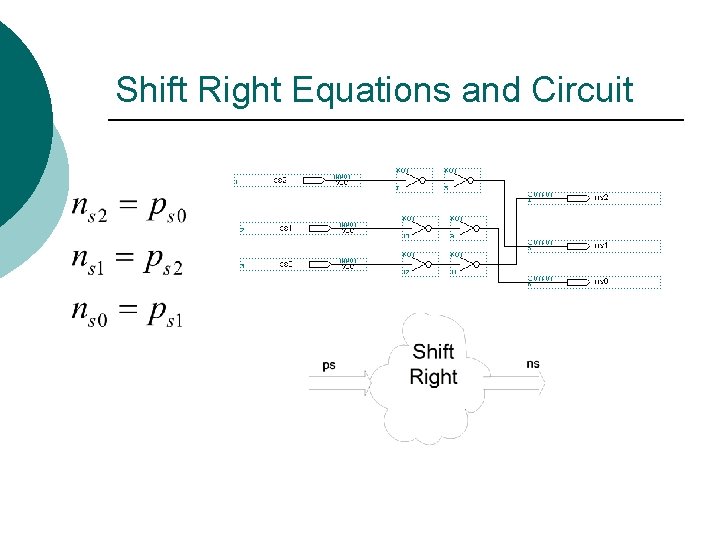
Shift Right Equations and Circuit

Synchronous Reset Module

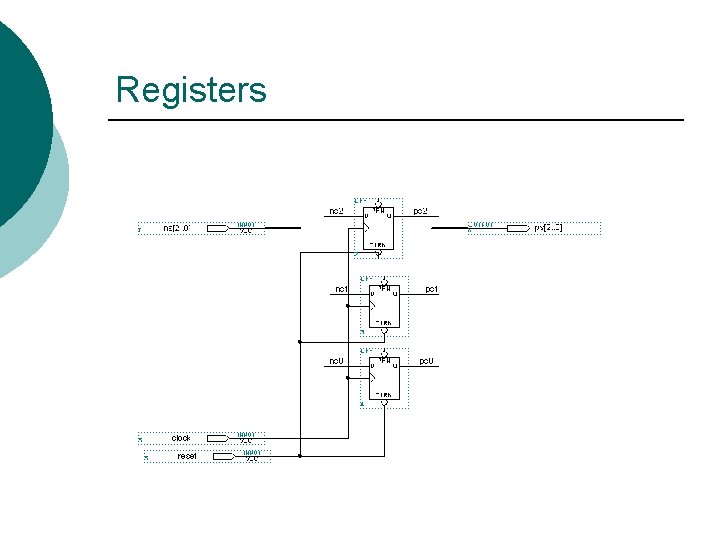
Registers

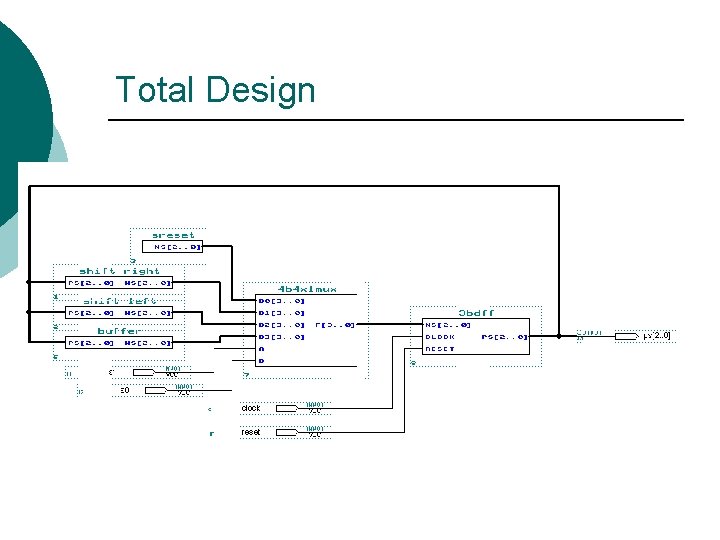
Total Design