Falling Objects Chapter 2 Section 3 FREE FALL

Falling Objects Chapter 2 Section 3

FREE FALL • • On August 2, 1971, a demonstration was conducted on the moon by astronaut David Scott. He simultaneously released a hammer and a feather from the same height above the moons surface. Result: Hammer and feather both fell down and landed at exactly the same moment. Conclusion: They both traveled the same displacement in the same amount of time.

Freely falling bodies undergo constant acceleration • • It is now well known that in the absence of air resistance all objects dropped near the surface of the planet fall with the same constant acceleration, referred to as free fall. Free fall- motion of an object falling with a constant acceleration.

Free fall example • • • The amount of time that passed between the 1 st and 2 nd images is equal to the amount of time that passed between the 4 th and 5 th images. The picture however shows that the t 0 displacement was not constant: t 1 sec What might be the cause of this? t 2 sec Velocity was not constant t 3 sec So this tells us that the apple and the feather were accelerating. t 4 sec t 5 sec

Compare the displacement between (t 1 - t 2) to that of (t 2 -t 3) � As you can see, within each time interval the displacement of the feather increased by the same amount as the displacement of the apple. � Since the time intervals are the t 0 same, we know velocity for both objects is increasing by the same t 1 sec amount in each time interval. t 2 sec � Thus; the apple and the feather t 3 sec are falling with the same constant t 4 sec acceleration. � Both will fall at the same rate t 5 sec regardless of the value of g.

fall is denoted with the symbol (g). � At the surface of Earth the magnitude of g is approximately 9. 81 m/s 2. � This acceleration is directed downward, toward the center of the Earth. � What would we say a downward direction is on are graphing system? Negative � Thus, the acceleration of objects in freefall near the surface of the Earth is…. � Free a=-g=-9. 81 m/s 2

What goes up must come down � Everyday experience shows us this simple fact, an object we throw in the air will continue to move upward for some time, stop momentarily at the peak, and then changes direction. � Because the object changes direction, it may seem like the velocity and acceleration are both changing. � Actually, objects thrown into the air have a downward acceleration as soon as they are released.

Why is this? � Because the ball undergoes constant acceleration, the ball’s speed is the same going up as it is going down at any point in the objects flight.

� As soon as the ball is released with an initial upward velocity of +10. 5 m/s, it has an acceleration of -9. 81 m/s 2. � After 1. 0 s (∆t=1. 0 s) the ball’s � Velocity will change by -9. 81 m/s to 0. 69 m/s upward. � After 2. 0 s (∆t=2. 0 s) the ball’s velocity will again change by -9. 81 m/s, to -9. 12 m/s. vi=+10. 5 m/s a=-9. 81 m/s 2

� There is an instant when the velocity of the ball is equal to 0 m/s. (at its peak upward motion) � Although the velocity is zero at the instant the ball reaches the peak, the acceleration is equal to -9. 81 m/s 2 at every instant regardless of the magnitude or direction of the velocity. � Thus, at the peak acceleration is -9. 81 m/s 2 at the peak even when velocity is zero. �A way to better understand this is to note; at the exact peak instant when (v=0 m/s) acceleration causes a change in direction of the velocity.

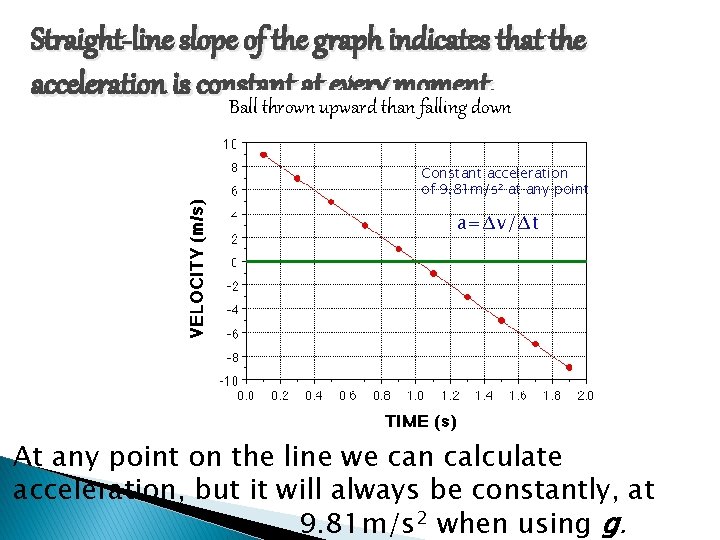
Straight-line slope of the graph indicates that the acceleration is constant at every moment. Ball thrown upward than falling down Constant acceleration of 9. 81 m/s 2 at any point a=∆v/∆t At any point on the line we can calculate acceleration, but it will always be constantly, at 9. 81 m/s 2 when using g.

Free falling objects � Always have the same downward acceleration. � Knowing this makes it easy to calculate the velocity, time, and displacement of many different motions using the equations for constantly accelerated motion. � Because the acceleration is the same throughout the entire motion, you can analyze the motion of a freely-falling object during any time interval.