Faculty of Computer Science Representing Information Numbers and

Department of Computing Science Slide’s source Yale N. Patt and Sanjay J. Patel, Introduction to Computing Systems: From bits & gates to C & Beyond, Mc. Graw. Hill Press, 2001, Chapter 2. CMPUT 229 © 2006

Department of Computing Science Positional Number System 329 3 2 9 923 9 2

Department of Computing Science Positional Number System 329 923 3 102 + 2 101

Department of Computing Science Positional Number System The same positional system works with different basis: 32913 92313 3 132 + 2 131 + 9 130 9 132 + 2 131 + 3 130 3 16910 + 2 1310 + 9 110 50710 + 2610 + 910 9 16910 + 2 1310 + 3 110 152110 + 2610 + 310 54210 155010 CMPUT 229 © 2006

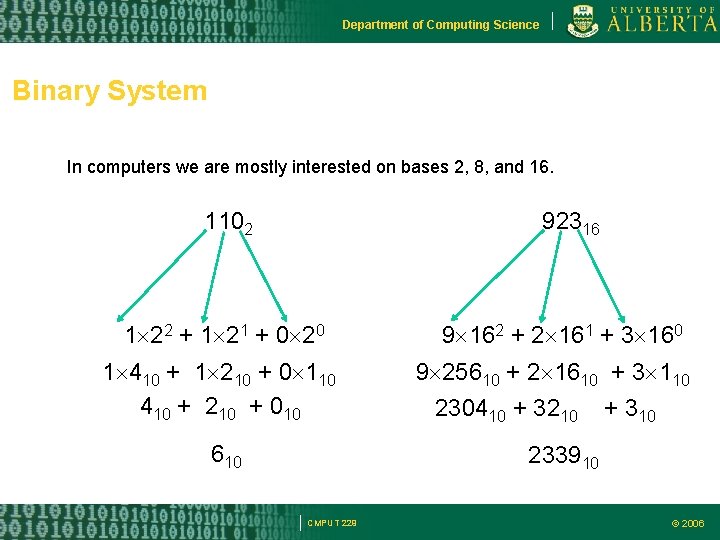
Department of Computing Science Binary System In computers we are mostly interested on bases 2, 8, and 16. 1102 92316 1 22 + 1 21 + 0 20 1 410 + 1 210 + 0 110 410 + 210 + 010 610 9 162 + 2 161 + 3 160 9 25610 + 2 1610 + 3 110 230410 + 3210 + 310 233910 CMPUT 229 © 2006

Department of Computing Science Signed Integers – Problem: given 2 k distinct patterns of bits, each pattern with k bits, assign integers to the patterns in such a way that: • The numbers are spread in an interval around zero without gaps. • Roughly half of the patterns represent positive numbers, and half represent negative numbers. • When using standard binary addition, given an integer n, the following property should hold: pattern(n+1) = pattern(n) + pattern(1) CMPUT 229 © 2006

Department of Computing Science Sign-Magnitude Representation In a sign-magnitude representation we use the first bit of the pattern to indicate if it is a positive or a negative number. CMPUT 229 © 2006

Department of Computing Science Sign-Magnitude Represetation What do we do with the pattern 1000?

Department of Computing Science Sign-Magnitude Representation Having two patterns to represent 0 is wasteful. The sign-magnitude representation has the advantage that it is easy to read the value from the pattern. But does it have the binary arithmetic property? For instance, what is the result of pattern(-1) + pattern(1)? 1001 + 0001 ? ? CMPUT 229 pattern(-1) pattern(1) Patt. Patel, pp. 20 © 2006

Department of Computing Science Sign-Magnitude Representation Having two patterns to represent 0 is wasteful. The sign-magnitude representation has the advantage that it is easy to read the value from the pattern. But does it have the arithmetic property? For instance, what is the result of pattern(-1) + pattern(1)? 1001 pattern(-1) + 0001 pattern(1) 1010 = ? ? CMPUT 229 Patt. Patel, pp. 20 © 2006

Department of Computing Science Sign-Magnitude Representation Having two patterns to represent 0 is wasteful. The sign-magnitude representation has the advantage that it is easy to read the value from the pattern. But does it have the arithmetic property? For instance, what is the result of pattern(-1) + pattern(1)? 1001 pattern(-1) + 0001 pattern(1) 1010 = pattern(-2) CMPUT 229 Patt. Patel, pp. 20 © 2006

Department of Computing Science 1’s-Complement Representation A negative number is represented by “flipping” all the bits of a positive number. We still have two patterns for 0. It is still easy to read a value from a given pattern. How about the arithmetic property? Suggestion: try the following -1 + 1 = ? ? -0 + 1 = ? ? CMPUT 229 Patt. Patel, pp. 20 © 2006

Department of Computing Science 2’s-Complement Representation A single pattern for 0. 1111 pattern(-1) + 0001 pattern(1) 0000 = pattern(0) It holds the arithmetic property. But the reading of a negative pattern is not trivial. CMPUT 229 Patt. Patel, pp. 20 © 2006

Department of Computing Science Binary to Decimal Conversion Problem: Given an 8 -bit 2’s complement binary number: a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 find its corresponding decimal value. Because the binary representation has 8 bits, the decimal value must be in the [-27; +(27 -1)] =[-128; +127] interval. CMPUT 229 Patt. Patel, pp. 23 © 2006

Department of Computing Science Binary to Decimal Conversion a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 Solution: negative false if (a 7 = 1) then negative true flip all bits; compute magnitude using: if (negative = true) then CMPUT 229 Patt. Patel, pp. 24 © 2006

Department of Computing Science Binary to Decimal Conversion (Examples) Convert the 2’s complement integer 11000111 to its decimal integer value. 1. a 7 is 1, thus we make a note that this is a negative number and invert all the bits, obtaining: 00111000 2. We compute the magnitude: 3. Now we remember that it was a negative number, thus: CMPUT 229 Patt. Patel, pp. 24 © 2006

Department of Computing Science Decimal to Binary Convertion We will start with an example. What is the binary representation of 10510? Our problem is to find the values of each ai Because 105 is odd, we know that a 0 = 1 Thus we can subtract 1 from both sides to obtain: CMPUT 229 Patt. Patel, pp. 24 © 2006

Department of Computing Science Decimal to Binary Convertion (cont. ) Now we can divide

Department of Computing Science Decimal to Binary Convertion (cont. ) a 4 = 0 a 5 = 1 a 6 = 1 Thus we got: a 6 = 1 a 5 = 1 a 4 = 0 a 3 = 1 a 2 = 0 a 1 = 0 a 0 = 1 10510 = 011010012 CMPUT 229 Patt. Patel, pp. 25 © 2006

Department of Computing Science Decimal to Binary Conversion (Another Method) We can also use repeated long division: 105/2 = 52 remainder 1 52/2 = 26 remainder 0 26/2 = 13 remainder 0 13/2 = 6 remainder 1 6/2 = 3 remainder 0 3/2 = 1 remainder 1 1/2 = 0 remainder 1 CMPUT 229 © 2006

Department of Computing Science Decimal to Binary Conversion (Another Method) We can also use repeated long division: 105/2 = 52 remainder 1 rightmost digit 52/2 = 26 remainder 0 26/2 = 13 remainder 0 13/2 = 6 remainder 1 10510 = 011010012 6/2 = 3 remainder 0 3/2 = 1 remainder 1 1/2 = 0 remainder 1 CMPUT 229 © 2006

Department of Computing Science Decimal to Binary Conversion (Negative Numbers) What is the binary representation of -10510 in 8 bits? We know from the previous slide that: +10510 =011010012 To obtain the binary representation of a negative number we must flip all the bits of the positive representation and add 1: 10010110 + 00000001 10010111 CMPUT 229 Thus: -10510 =100101112 Patt. Patel, pp. 22 -23 © 2006

Department of Computing Science Hexadecimal Numbers (base 16) In the 68 K assembler, by convention, the character $ is printed in front of an hexadecimal number to indicate base 16. If the number $FACE represents a 2’s complement binary number, what is its decimal value? First we need to look up the binary representation of F, which is 1111. Therefore $FACE is a negative number, and we have to flip all the bits. CMPUT 229 Patt. Patel, pp. 26 -27 © 2006

Department of Computing Science Hexadecimal Numbers (base 16) It is best to write down the binary representation of the number first: $FACE = 1111 1010 1100 1110 Now we flip all the bits and add 1: 0000 0101 0011 0001 + 0000 0001 0000 0101 0010 = $0532 Then we convert 0 x 0532 from base 16 to base 10: $0532 = 0 163 + 5 162 + 3 161 + 2 160 = 0 + 5 256 + 3 16 + 2 1 = 1280 + 48 + 2 = 133010 $FACE = -133010 CMPUT 229 Patt. Patel, pp. 26 -27 © 2006

Department of Computing Science Binary Arithmetic Decimal Binary 19 + 3 22 010011 + 000011 010110 Binary Decimal 14 - 9 5 910 = 0010012 -910 = 1101112 CMPUT 229 001110 + 110111 000101 Patt. Patel, pp. 25 © 2006

Department of Computing Science Overflow What happens if we try to add +9 with +11 in a 5 -bit 2 -complement representation? Decimal Binary 9 + 11 20 01001 + 01011 10100 = -12 ? The result is too large to represent in 5 digits, i. e. it is larger than 01111 = +1510. When the result is too large for the representation we say that the result has OVERFLOWed the capacity of the representation. CMPUT 229 Patt. Patel, pp. 27 © 2006

Department of Computing Science Overflow Detection What happens if we try to add +9 with +11 in a 5 -bit 2 -complement representation? Decimal Binary 9 + 11 20 01001 + 01011 10100 = -12 ? We can easily detect the overflow by detecting that the addition of two positive numbers resulted in a negative result. CMPUT 229 Patt. Patel, pp. 28 © 2006

Department of Computing Science Overflow (another example) Could overflow happen when we add two negative numbers? Decimal Binary - 12 + -6 -18 10100 + 11010 01110 = +14 ? Again we can detect overflow by detecting that we added two negative numbers and got a positive result. Could we get overflow when adding a positive and a negative number? CMPUT 229 Patt. Patel, pp. 28 © 2006

Department of Computing Science Sign-extension What is the 8 -bit representation of +510? 0000 0101 What is the 16 -bit representation of +510? 0000 0101 What is the 8 -bit representation of -510? 1111 1011 What is the 8 -bit representation of -510? 1111 1011 CMPUT 229 Patt. Patel, pp. 27 © 2006

Department of Computing Science Sign-extension What is the 8 -bit representation of +510? 0000 0101 What is the 16 -bit representation of +510? 0000 0101 What is the 8 -bit representation of -510? 1111 1011 To sign-extend a number to a larger representation, all we have to do is to replicate the sign bit until we obtain the new length. What is the 8 -bit representation of -510? 1111 1011 CMPUT 229 Patt. Patel, pp. 27 © 2006

Department of Computing Science Some Useful Numbers to Remember 20 = 110 = $0001 210 = 102410 = 0100 0000 = $0400 = 1 K 21 = 210 = $0002 22 = 410 = $0004 23 = 810 = $0008 220 = 210 × 210 = 102410 × 102410 = 0001 0000 0000 = $0010 0000 = 1 M 24 = 1610 = $0010 25 = 3210 = $0020 26 = 6410 = $0040 230 = 210 × 210 = 1 G 27 = 12810 = $0080 28 240 = 210 × 210 = 1 T = 25610 = $0100 29 = 51210 = $0200 CMPUT 229 © 2006

Department of Computing Science Data and Addresses “She is 104. ” In each case, how do we know what 104 is? “I am staying at 104. ” From the context in which it is used! The same is true for data and addresses. The same number is data on one instance and address on another. “It costs 104. ” “There is 104. ” “My office is 104. ” “Write 100 at $0780. ” “Stop in front of 104. ” “Write 100 at 100. ” “My house is 104. ” CMPUT 229 © 2006

Department of Computing Science Representing Fractions In base 10 we know that: +0. 10510 = 10510/100010 = 10510/103 Fractions are represented in a similar fashion in base 2: +0. 101012 = 101012/1000002 = 101012/25 101012 = 2110 and 25 = 32, thus 0. 101012 = 2110/3210 = 0. 6562510 CMPUT 229 Clements, pp. 152 © 2006

Department of Computing Science Fractions: Binary to Decimal Another way to convert a binary fraction into a decimal value is as follows: 0. 101012 = 1 2 -1 + 0 2 -2 + 1 2 -3 + 0 2 -4 + 1 2 -5 = 1 0. 5 + 0 0. 25 + 1 0. 125 + 0 0. 0625 + 1 0. 03125 = 0. 5 + 0. 125 + 0. 03125 = 0. 65625 CMPUT 229 © 2006

Department of Computing Science Fractions: Decimal to Binary The following method works to convert decimal factions to binary: 0. 687510 = ? ? 2 0. 6875 2 = 1. 3750 0. 3750 2 = 0. 7500 2 = 1. 5000 0. 5000 2 = 1. 0000 0. 0000 2 Done! 0. 687510 = 0. 10112 CMPUT 229 © 2006