Factorizations and Decompositions Square or Rectangular Matrices QR

Factorizations and Decompositions Square or Rectangular Matrices QR factorization Reduced QR factorization SVD Reduced SVD

Factorizations and Decompositions Square Matrices LU factorization Cholesky factorization Schur Factorization Arnoldi iteration Lanczos iteration Eigenvalue decomposition

Core Problem Three fundamental problems are considered 1) Square system of linear equations 2) Least Square Problem: m>n 3) Eigenvalue Problem (2 hw 4)

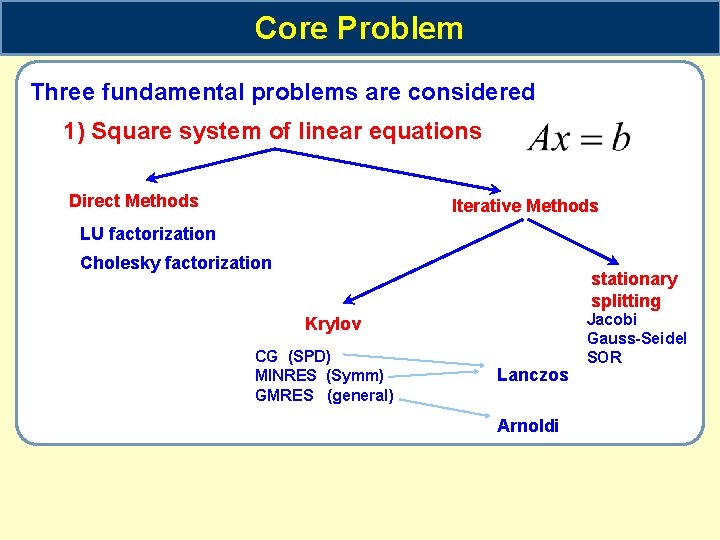
Core Problem Three fundamental problems are considered 1) Square system of linear equations Direct Methods Iterative Methods LU factorization Cholesky factorization stationary splitting Krylov CG (SPD) MINRES (Symm) GMRES (general) Lanczos Arnoldi Jacobi Gauss-Seidel SOR

Core Problem Three fundamental problems are considered 2) Least Square Problem: m>n Normal Equation QR-factorization SVD

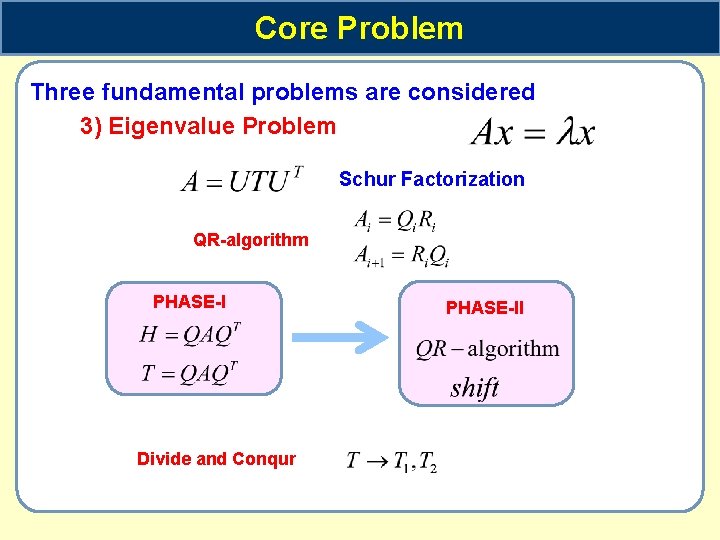
Core Problem Three fundamental problems are considered 3) Eigenvalue Problem Schur Factorization QR-algorithm PHASE-I Divide and Conqur PHASE-II

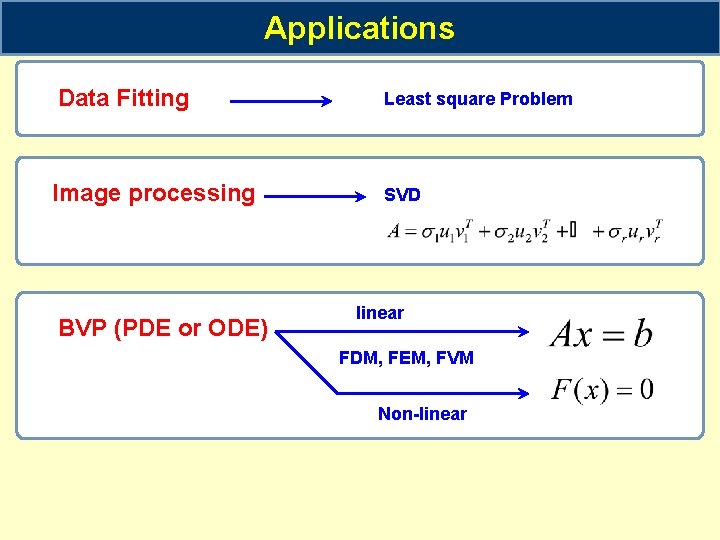
Applications Data Fitting Image processing BVP (PDE or ODE) Least square Problem SVD linear FDM, FEM, FVM Non-linear

Applications Non-linear system of equations: Newton Raphson Method: Single variable jacobian In Newton Raphson Method, each iteration requires solving one linear system of equations

Norms and Stability Vector p-norm Matrix p-norm Frobenius norm: Condition number

Norms and Stability A well-conditioned Problem Is one with the property that all small changes in initial data lead to only small changes in the solution An ill-conditioned Problem Is one with the property that some small changes in initial data lead to a large change in the solution Frobenius norm: Condition number

MATLAB LU factorization: lu, luinc Cholesky factorization: chol, cholinc Eigenvalue decomposition: eig QR factorization: qr Singula Value Decompsition: svd Schur Factorization: schur Arnoldi, Lanczos: hess Conjugate Gradient: pcg Minimal Residuals: minres Generalized Minimal Residuals: gmres Solving linear system: Ab Least Square Problem: lsqr

References Trefethen: encyclopedia PDE in Fluid and its iterative an in-depth, up-to-date view of practical algorithms for solving largescale linear systems of equations Focuses on the use of iterative methods for solving large sparse systems of linear equations

References

software library for numerical linear algebra LAPACK LINPACK NAG (The Numerical Algorithms Group) IMSL BLAS www. netlib. org

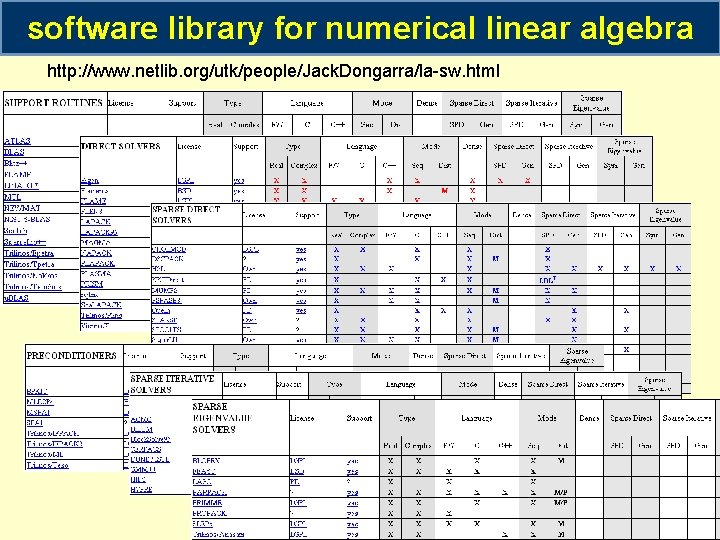
software library for numerical linear algebra http: //www. netlib. org/utk/people/Jack. Dongarra/la-sw. html

software library for numerical linear algebra FORTRAN c Parallel distributed methods Iterative methods for sparse and structured linear systems

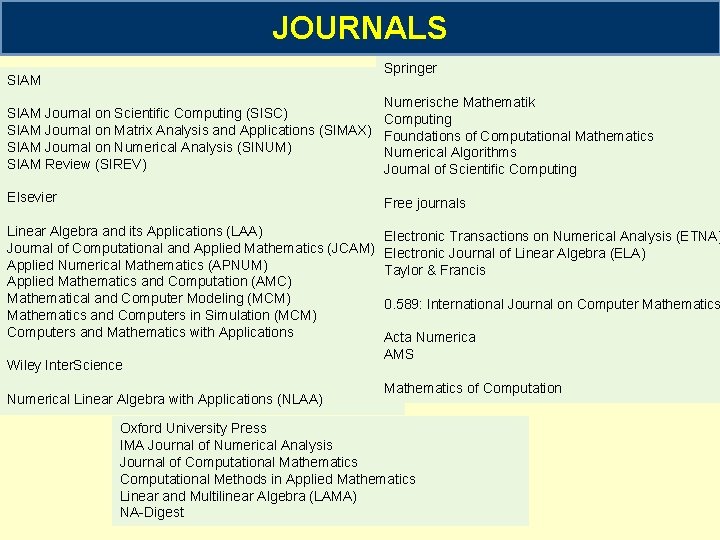
JOURNALS Springer SIAM Journal on Scientific Computing (SISC) SIAM Journal on Matrix Analysis and Applications (SIMAX) SIAM Journal on Numerical Analysis (SINUM) SIAM Review (SIREV) Numerische Mathematik Computing Foundations of Computational Mathematics Numerical Algorithms Journal of Scientific Computing Elsevier Free journals Linear Algebra and its Applications (LAA) Journal of Computational and Applied Mathematics (JCAM) Applied Numerical Mathematics (APNUM) Applied Mathematics and Computation (AMC) Mathematical and Computer Modeling (MCM) Mathematics and Computers in Simulation (MCM) Computers and Mathematics with Applications Electronic Transactions on Numerical Analysis (ETNA) Electronic Journal of Linear Algebra (ELA) Taylor & Francis Wiley Inter. Science Numerical Linear Algebra with Applications (NLAA) 0. 589: International Journal on Computer Mathematics Acta Numerica AMS Mathematics of Computation Oxford University Press IMA Journal of Numerical Analysis Journal of Computational Mathematics Computational Methods in Applied Mathematics Linear and Multilinear Algebra (LAMA) NA-Digest